Prepare to conquer your AKTU Btech Electromagnetic Field Theory examinations with our excellent resource, the 2021-22 Previous Year Question Paper! Explore Maxwell’s equations, electrostatics, magnetostatics, electromagnetic waves, and transmission lines. Practice with genuine questions from past years to improve your knowledge and exam preparation.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Electromagnetic Field Theory: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Section A : Important Short Question Electromagnetic Field
a. Find the value of (3âx + 6ây) × (2âx + 3ây + 5âz) , where x denotes cross product.
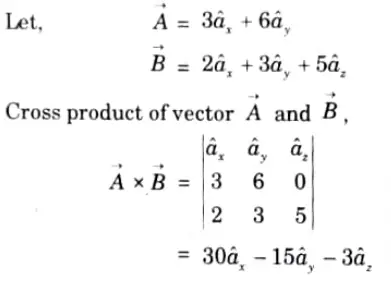
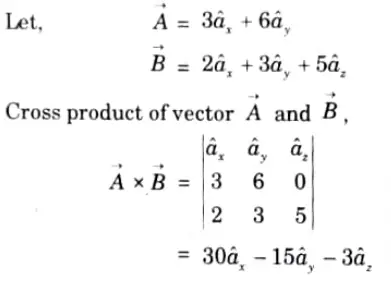
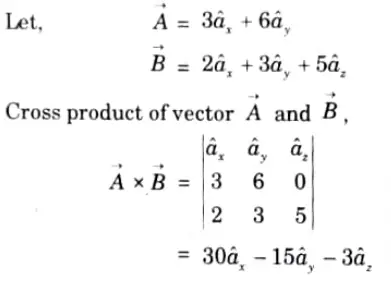
b. Find the unit vector of the vector ->A = (7âx + 2ây +8âz).
Ans. Unit vector of the vector ->A



c. Explain electric field intensity.
Ans. The electric field intensity![]()
![]()
![]()
![]()
![]()
i.e.,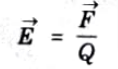
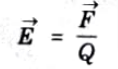
d. Prove that ![]()
![]()
![]()
![]()
![]()
Ans.
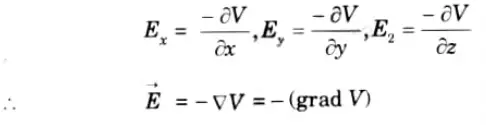
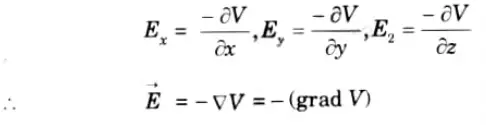
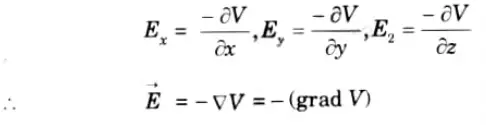
Comparing eq. (2.5.1) and (2.5.2) We get,
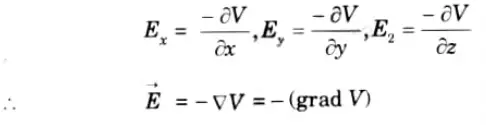
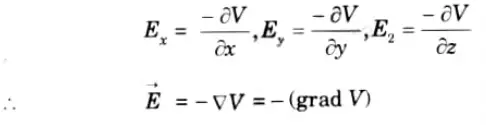
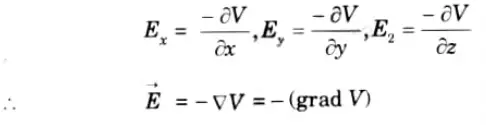
e. Prove that curl
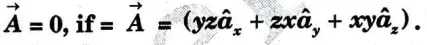
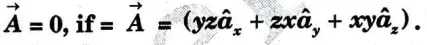
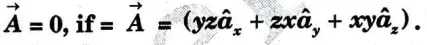
Ans.



f. Narrate the concept of electric dipole moment.
Ans. 1. It is the result of the size of the charges and their distance from one another. The dipole moment controls how powerful an electric dipole must be to generate an electric field.
2. Mathematically, the electric dipole moment is given by.
P = q x 2a
g. Explain the term ‘lnductance’.
Ans. An inductor, also known as inductance, is a passive part that stores magnetic energy in the form of a field.
h. Explain the concept of magnetic flux density.
Ans. The flux per unit Area (A), measured in a plane perpendicular to the flux is defined as the flux density. It is measured in Tesla (T) and denoted by B.
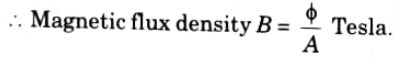
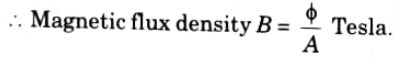
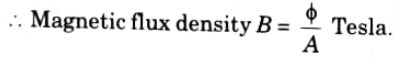
i. Explain the physical significance of Poynting vector.
Ans. Any closed surface’s net power flowing out can be calculated by integrating the Poynting vector over that surface.
j. Explain the reflection of a plane wave in a normal incidence.
Ans. If load impedance (ZL)is not equal to characteristic impedance (Z0) then mismatch occurs. In this case the part of the wave gets absorbed by the load while the rest part is reflected back to the source. Thus, due to mismatch in impedance the reflection occurs.
Section B
a. Given that 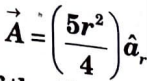
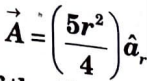
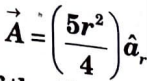
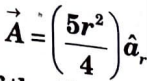

Ans. We know that
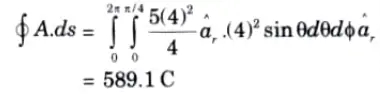
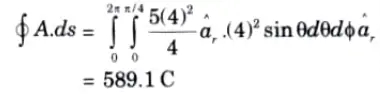
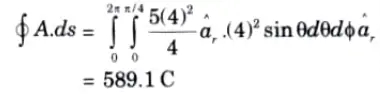
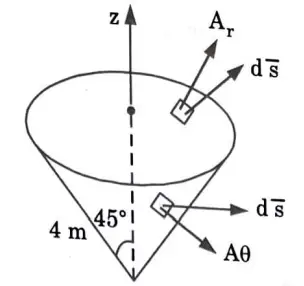
where, A has only a radial component. A.ds has a non-zero value on the surface r = 4 m.
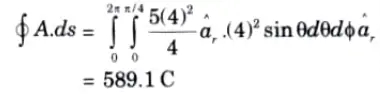
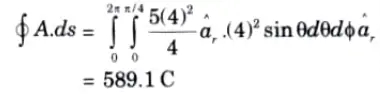
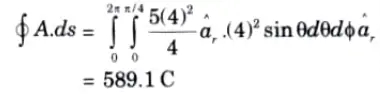
Divergence theorem gives
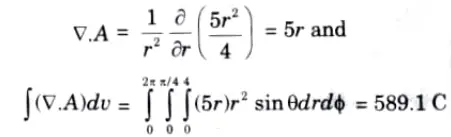
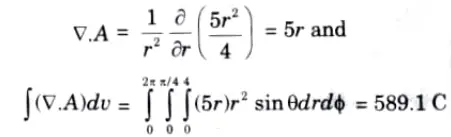
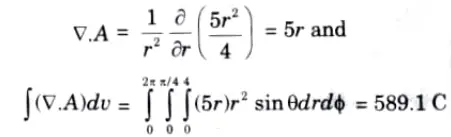
b. Derive the mathematical expression for energy stored in electric field. If V = yx2 + zx + xy V. Do the analysis of ![]()
![]()
![]()
![]()
![]()
Ans. 1. Consider the volume charge distribution with uniform charge density ρ C/m3. Therefore total energy stored is
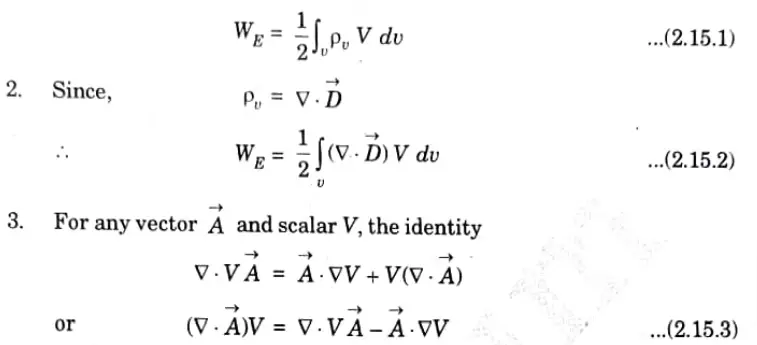
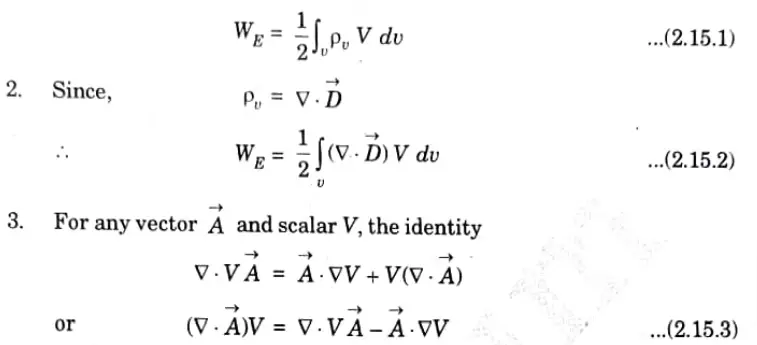
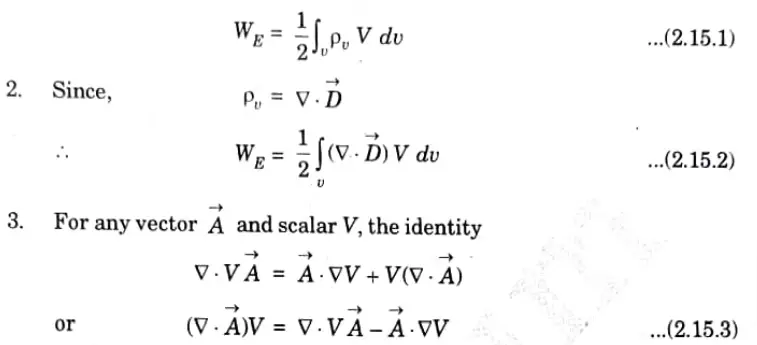
Applying the identity in eq. (2.15.3) to eq. (2.15.2), we get
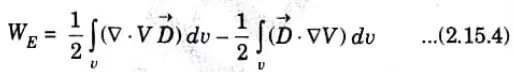
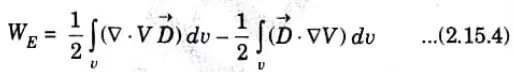
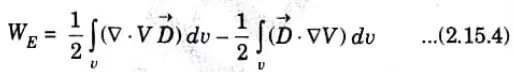
4. By applying divergence theorem to the first term on the right-hand side of eq. (2.15.4), we have
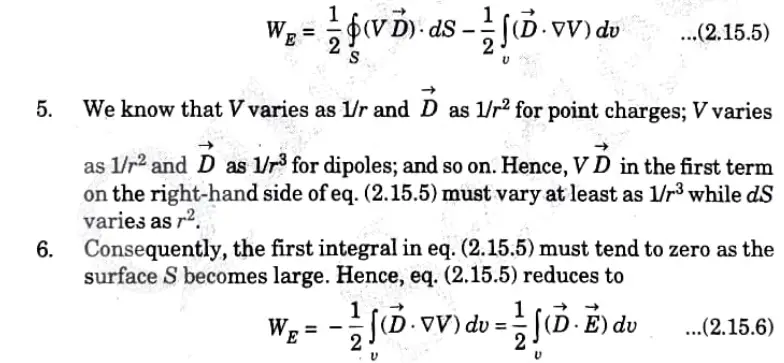
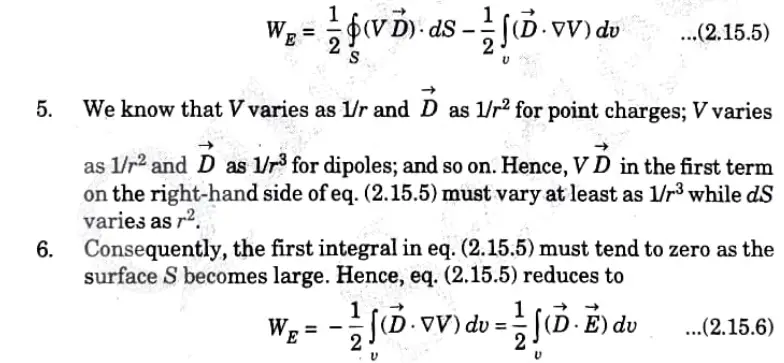
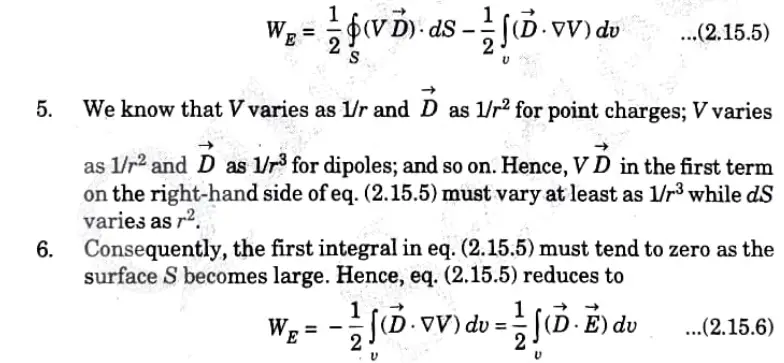
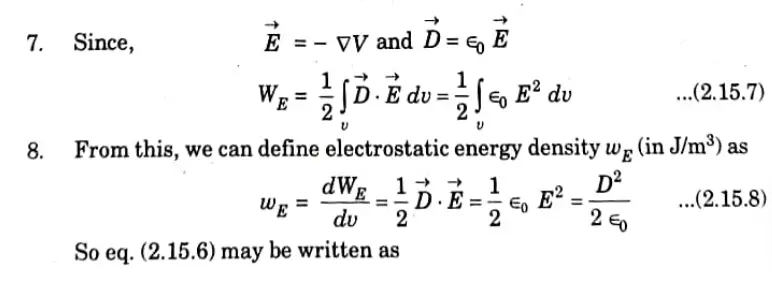
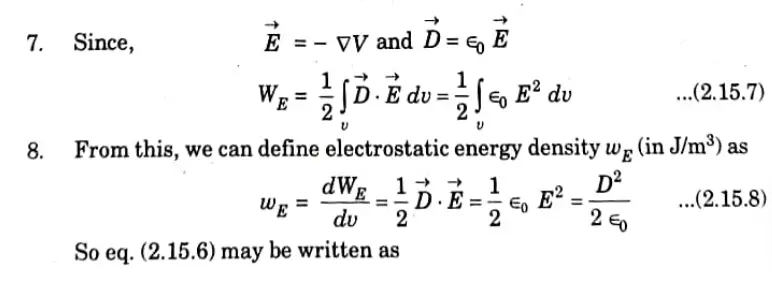
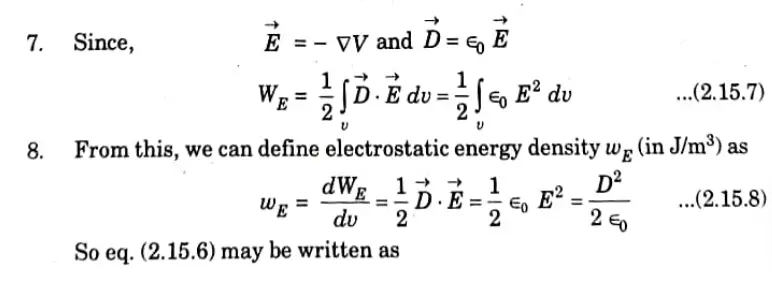
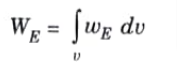
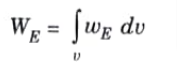
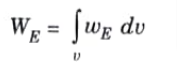
B. Numerical:
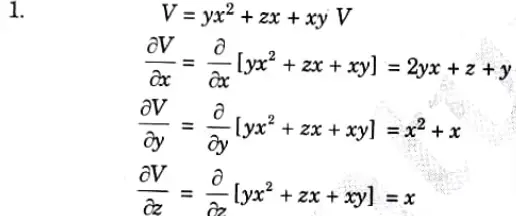
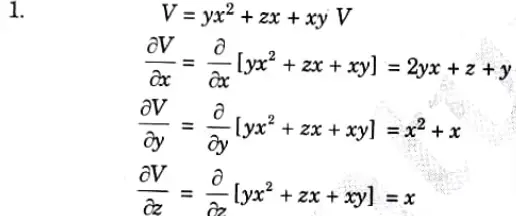
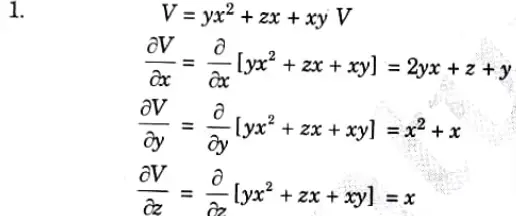
2. The electric field is given by
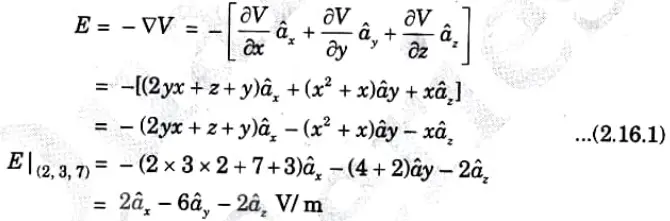
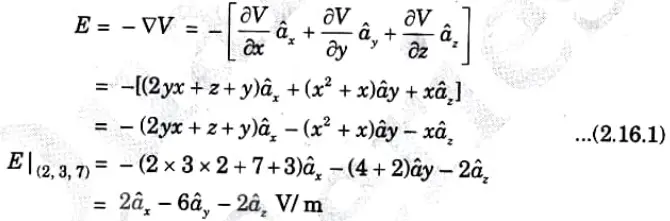
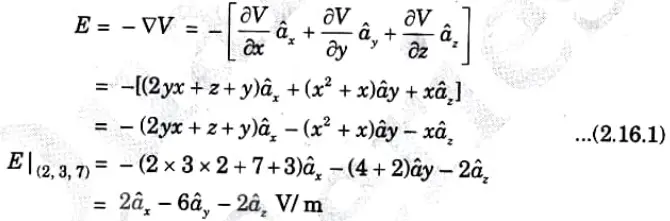
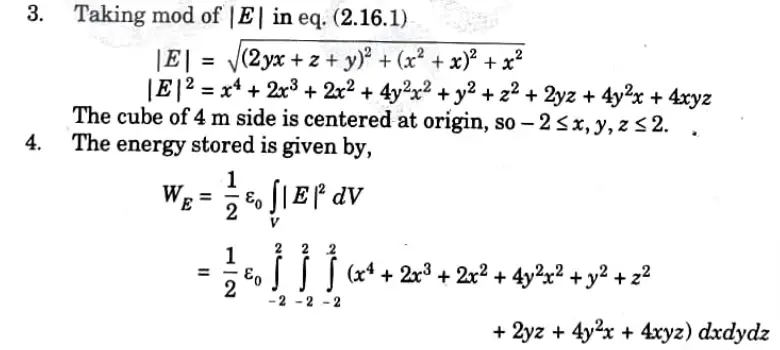
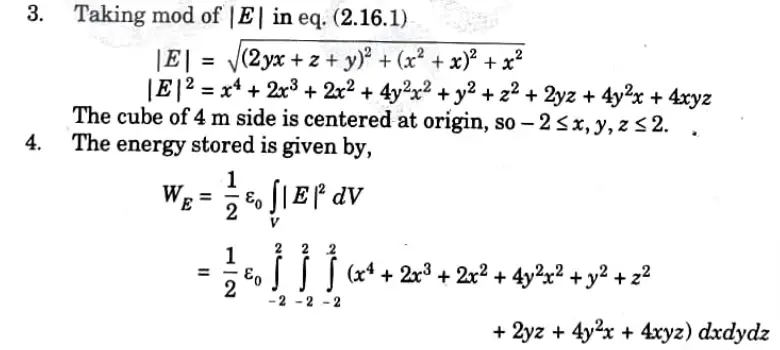
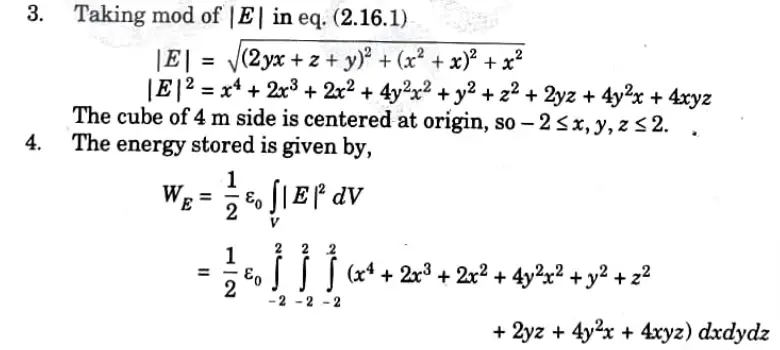
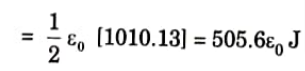
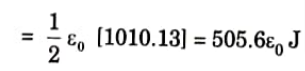
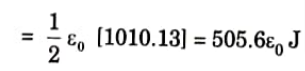
c. Explain Biot-Savart’s law. Find the magnetic field intensity for infinite line current.
Ans. 1. Biot-Savart’s law states that the differential magnetic field intensity dH produced at point P, as shown in Fig., by the differential current element I dl is proportional to the product I dl and sine of angle (α) between the element and the line joining point P to the element and is inversely proportional to the square of the distance R between P and the element.
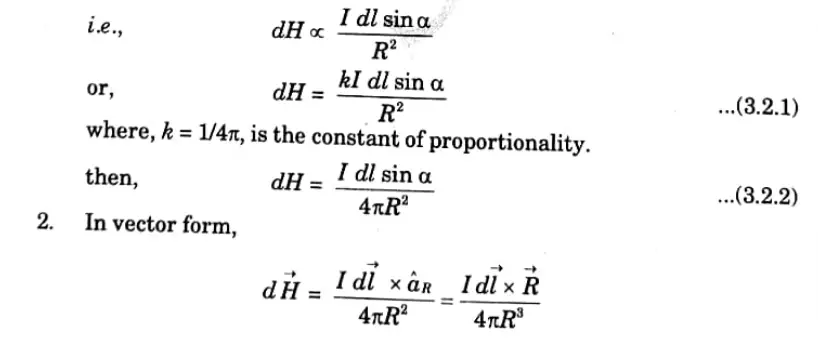
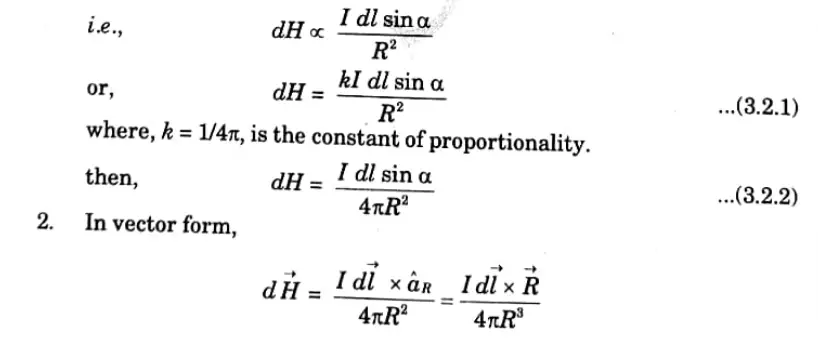
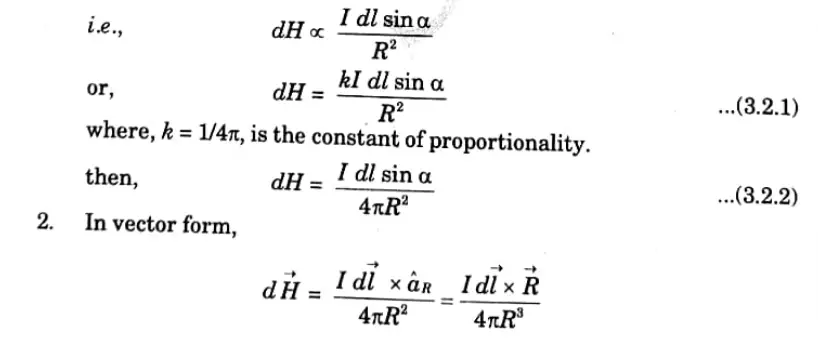


3. Biot-Savart’s law in terms of distributed current sources is given as :



d. Explain the Ampere circuital law. Derive two applications of ampere ‘s circuital law. Also, derive modified Maxwell’s equations.
Ans. A. Applications of ampere circuited law:
i. Infinite line current:
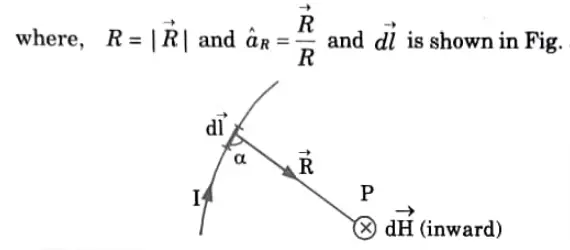
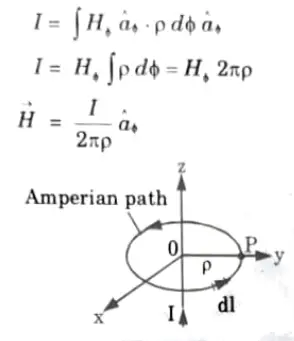
1. Consider an infinitely long filamentary current I along the z-axis as shown in the Fig.
2. To determine Vector H (->H)at point P, consider a closed path passing through point P. This is the path on which Ampere’s law is applied and it is known as Amperian path.
3. Since this path encloses the whole current I, then according to Ampere’s law,


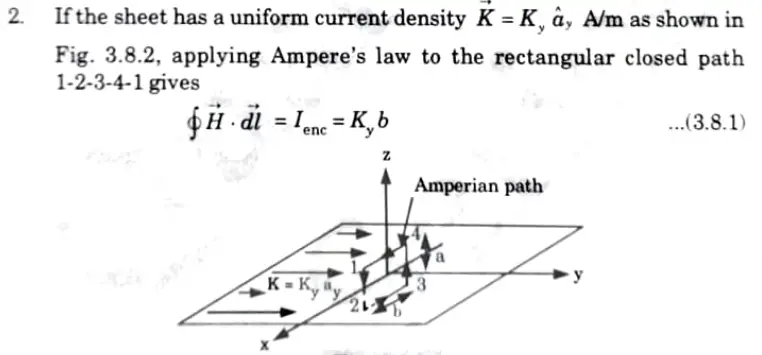
ii. Infinite sheet of current:
1. Consider an infinite current sheet in the z = 0 plane.


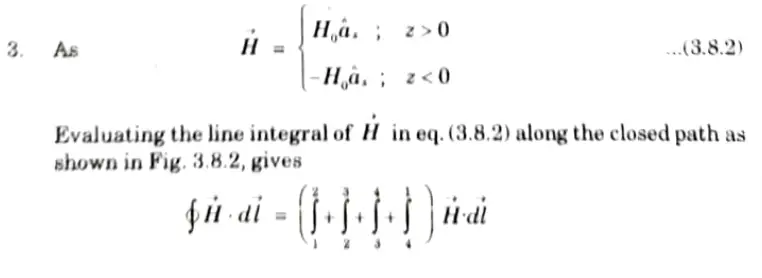
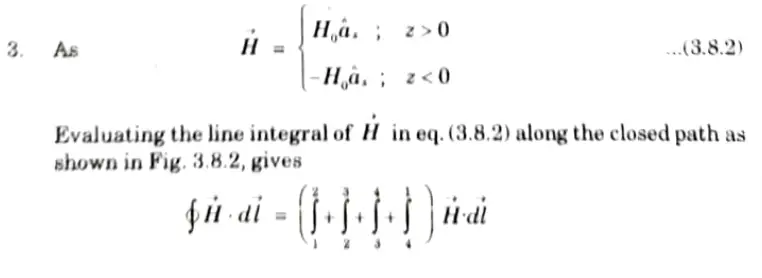
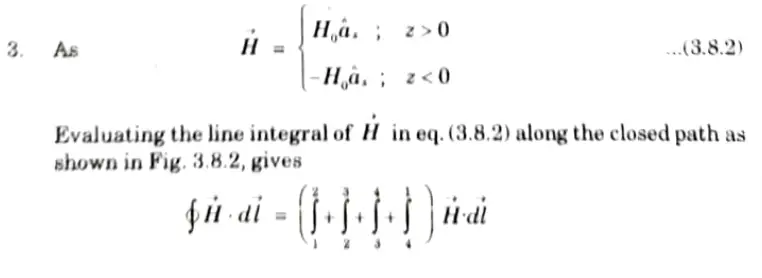






ii. Infinitely long coaxial transmission line:
1. Consider an infinitely long coaxial transmission line made up of two concentric cylinders with their axes aligned with the z-axis, as shown in Fig.
2. The outer conductor has an inner radius of b and thickness t and carries return current -I, whereas the inner conductor has a radius of a and carries current I.
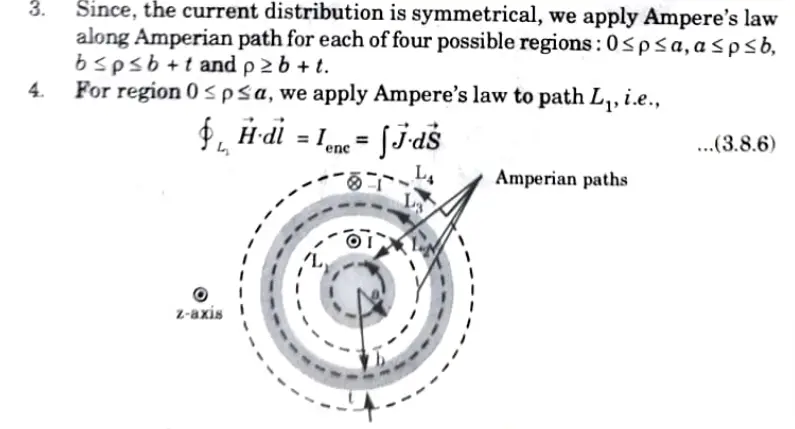


5. As the current is uniformly distributed over the cross-section,
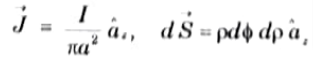
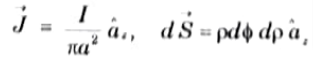
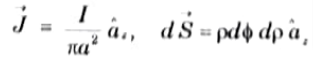









Maxwell equation from Ampere’s law:
1. Applying Stoke’s theorem in eq., we get
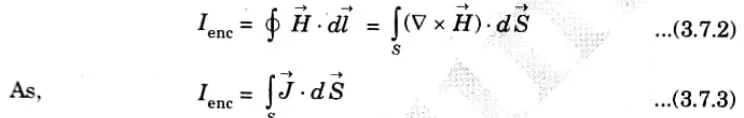
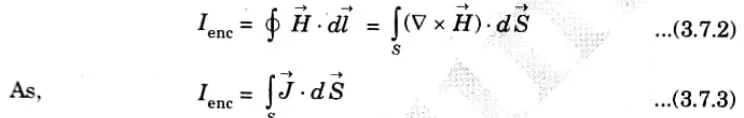
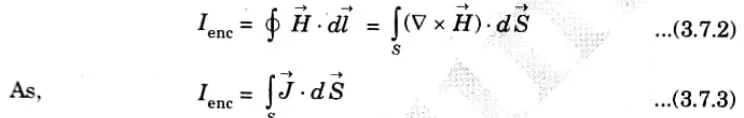
2. Comparing the surface integral in eq. (3.7.2) and (3.7.3) clearly indicates that



3. Eq. (3.7.4) is the third Maxwell’s equation.
e. Derive the mathematical equation for Poynting vector.
Ans. 1. Energy can be transported from one point to another point by means of EM waves. The rate of such energy transportation can be obtained from Maxwell’s equations:



2. Taking a dot product on both sides of eq. (5.17.2) with ![]()
![]()
![]()
![]()
![]()
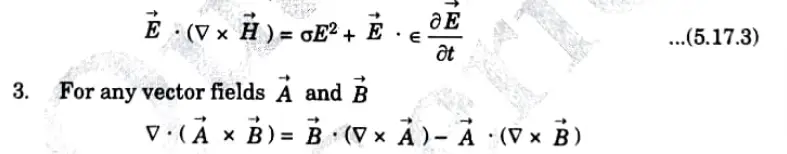
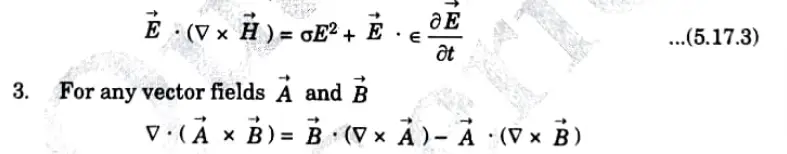
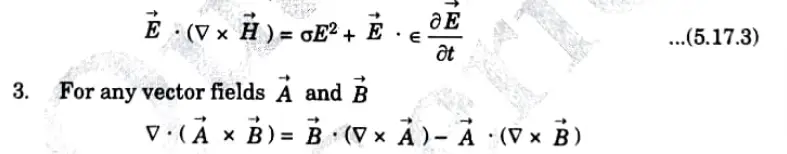






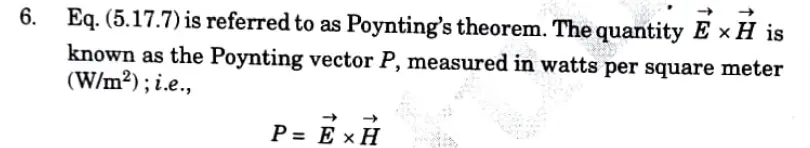
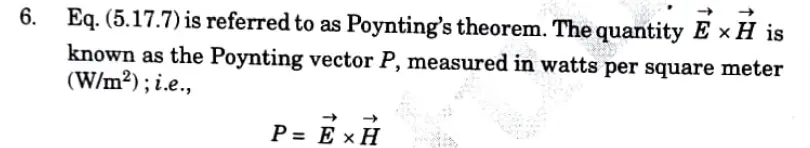
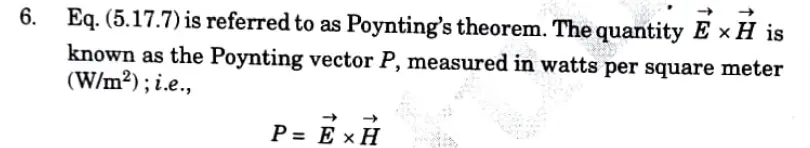
It represents the instantaneous power density vector associated with the EM field at a given point.
7. Any closed surface’s net power flowing out can be calculated by integrating the Poynting vector over that surface.
8.According to the Poynting theorem, the net power leaving a given volume v is equal to the rate at which the energy stored there is vanishing over time less Ohmic losses.
Section C Important Question
a. Investigate the values of X, Y and Z. If ![]()
![]()
![]()
![]()
Ans. 1. Vector ![]()
![]()
![]()
![]()
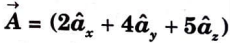
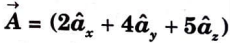
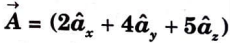
2. The component of ![]()
![]()
![]()
![]()
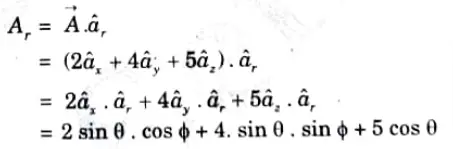
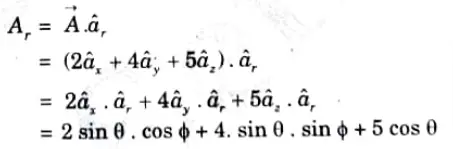
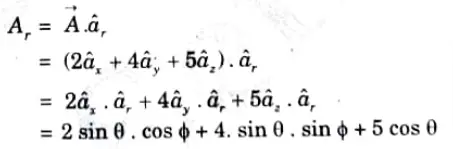
3. The component of ![]()
![]()
![]()
![]()
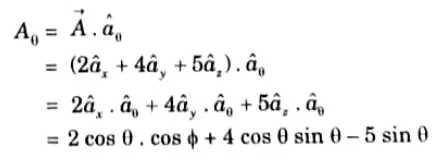
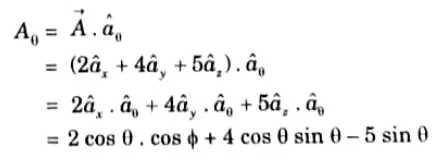
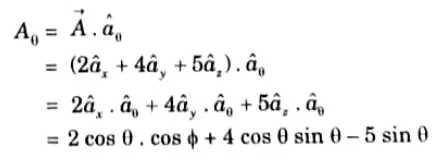
4. The component of direction is given by,![]()
![]()
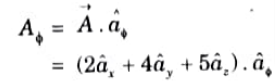
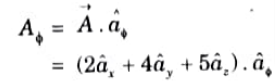
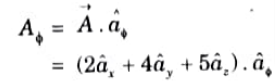
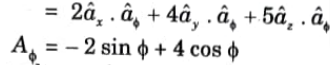
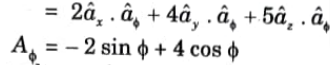
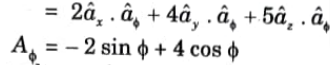
5. Collecting these results, we have



6. Comparing eq. (1.14.1) and (1.14.2), we get
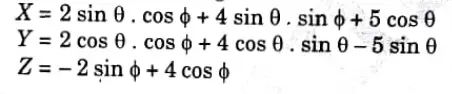
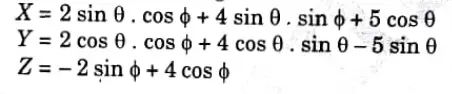
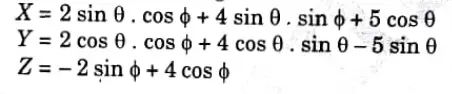
b. Derive the Poisson’s and Laplace equation in all coordinate systems.
Ans. A. Poisson’s and Laplace’s equation:
1. The equations of Poisson and Laplace are utilised to address the boundary value issues. Gauss’ law in point form can be used to create Poisson’s equation.
2. Gauss’s law in the point form is,
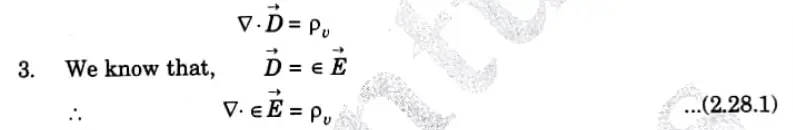
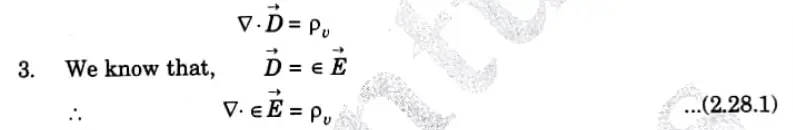
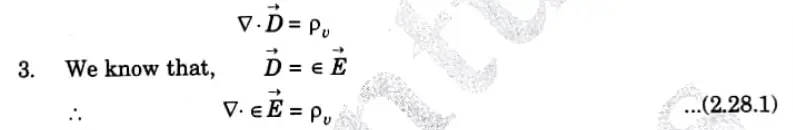
4. Now, from the gradient relationship,



5. Substituting eq. (2.28.2) in (2.28.1),



Eq. (2.28.3) is called Poisson’s equation.
6. Now, in dielectric medium, where volume charge density is zero (Pv = 0), the Poisson’s equation takes the form,
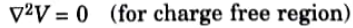
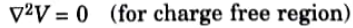
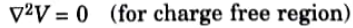
This is special case of Poisson’s equation and is called as Laplace’s equation.
B. Poisson’s equation in different coordinates systems:
1. Cartesian coordinates system,
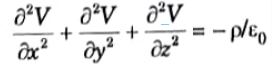
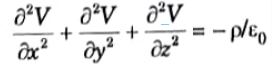
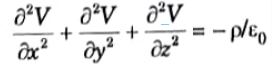
2. Cylindrical coordinates system,
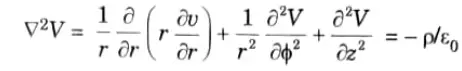
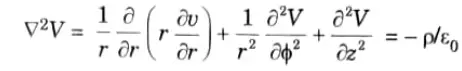
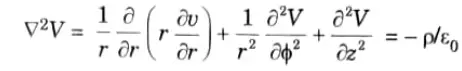
3. Spherical coordinates system,
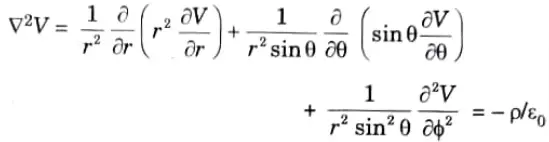
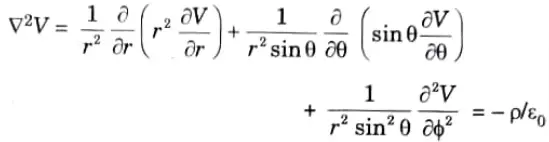
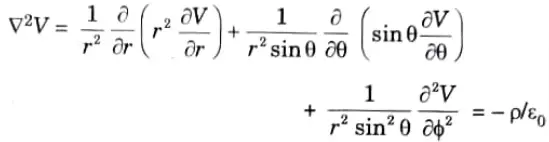
C. Laplace’s equation in different coordinate systems :
1. Cartesian coordinates system,
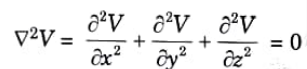
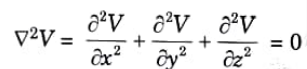
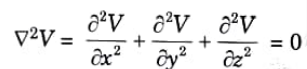
2. Cylindrical coordinates system,
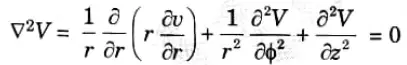
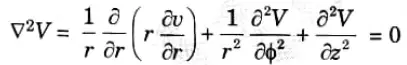
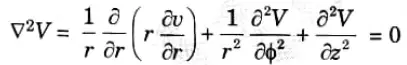
3. Spherical coordinates system,
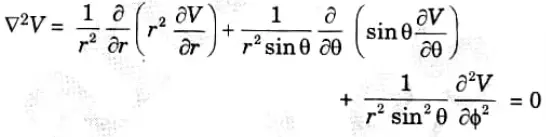
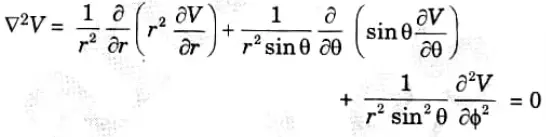
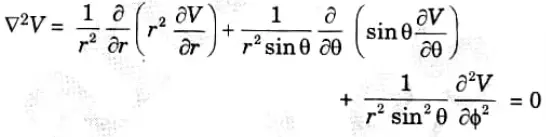
a. Point charges 1mC and -2mC are located at (3, 2, -1) and (-1, -1, 4), respectively. Calculate the electric force on a 10 nC charge located at (0, 3, 1) and the electric field intensity at that point.
Ans.
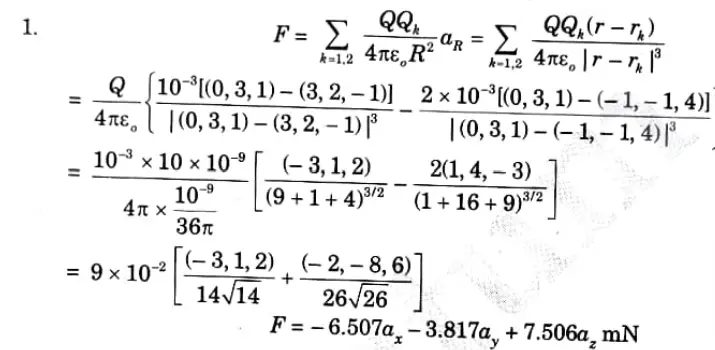
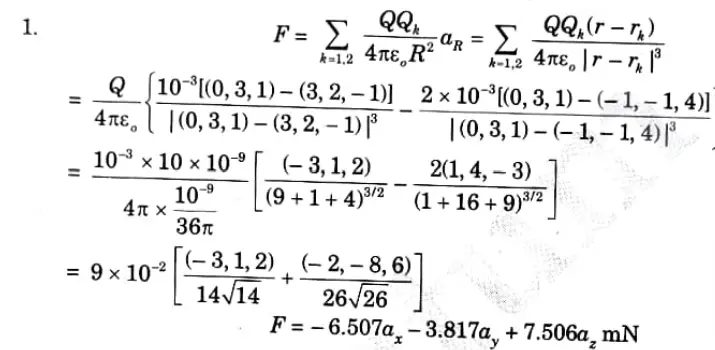
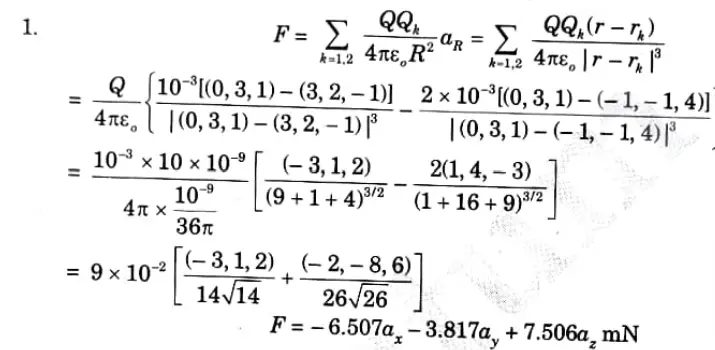
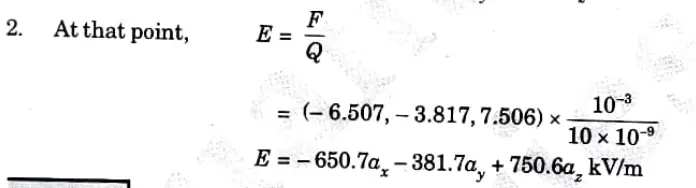
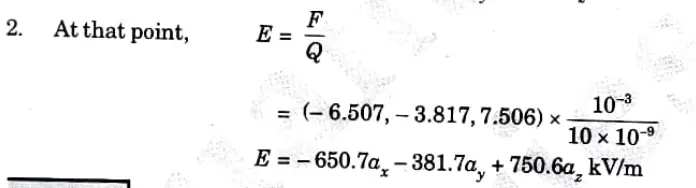
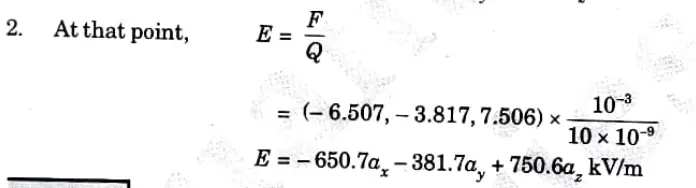
b. Given the potential 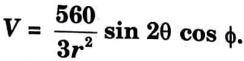
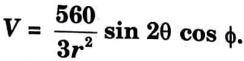
Ans.
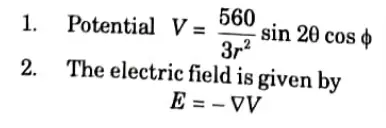
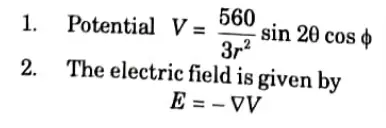
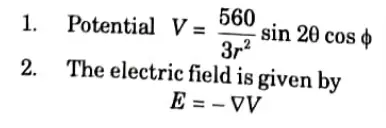






Section 5 Long Question with Answer
a. Explain convection and conduction currents. Derive mathematical equations also. Also derive the magnetic vector potential.
Ans. A. Magnetic scalar potential:
1. The magnetic scalar potential is written as Vm and is related to Vector H as



2. The curl of the magnetic field is given as
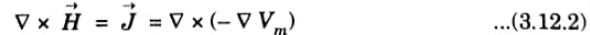
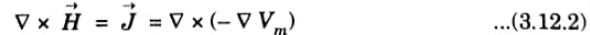
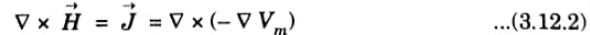
3. It is noticed that if magnetic field intensity is defined as the gradient of magnetic scalar potential, then current density is zero across the region in which scalar magnetic potential is defined because the curl of the gradient of any scalar identity is zero.Thus,
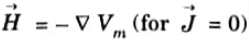
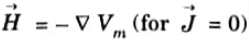
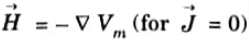
4. Since, Vm satisfies the Laplace’s equation just as V does for electrostatic fields.



5. The characteristics of scalar magnetic potential (Vm) are :
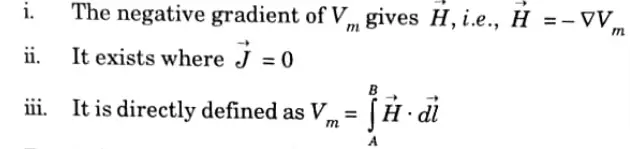
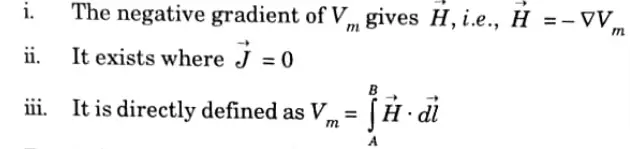
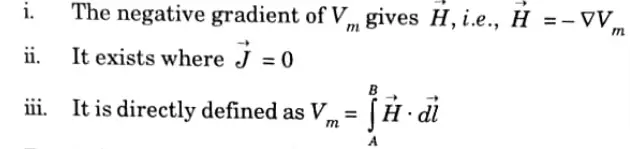
B. Magnetic vector potential:
1. Vector magnetic potential exists in regions where Vector J is present. It is defined in such a way that its curl gives the magnetic flux density, i.e.,
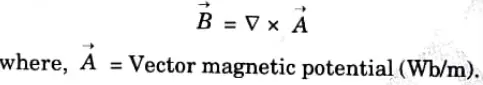
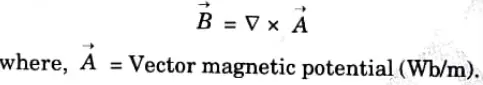
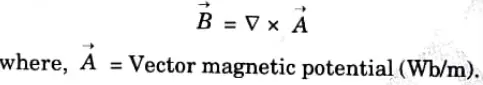
2. Vector A can also be defined for line current, for surface current and for volume current as;



3. The characteristics of vector magnetic potential are:
i. It exists even when Vector j is present.
ii. Vector magnetic potential Vector A has applications to obtain radiation characteristics of antennas, apertures and also obtain radiation leakages from transmission line , waveguides and microwave ovens.iii. Vector A is used to find near and far fields of antennas.
C. Convection and conduction current:
i. Convection current: Since conductors are not used in convection current, Ohm’s law is not satisfied. When current passes through an insulating media, such as a liquid, rarefied gas, or a vacuum, it happens.
ii. Conduction current: A conductor is necessary for current to flow. A conductor is made up of several free electrons that produce conduction current when an electric field is applied.
b. What is magnetic dipole ? Find magnetic vector potential. Explain the complete magnetic boundary conditions. Derive all tangential and normal components.
Ans. A. Magnetic dipole : Any magnetic dipole has a north pole and a south pole, which are two separate poles. Consequently, a basic bar magnet is referred to as a magnetic dipole. Every piece of this magnet, if broken into smaller parts, will form a dipole.
B. Magnetic vector potential :
1. Vector magnetic potential exists in regions where Vector J is present. It is defined in such a way that its curl gives the magnetic flux density, i.e.,
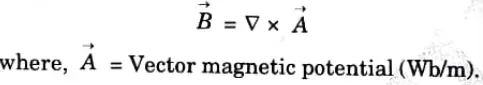
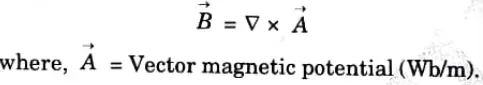
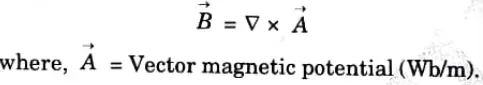
2. Vector A can also be defined for line current, for surface current and for volume current as;



3. The characteristics of vector magnetic potential are:
i. It exists even when Vector J is present.
ii. Vector magnetic potential Vector A has applications to obtain radiation characteristics of antennas, apertures and also obtain radiation leakages from transmission line , waveguides and microwave ovens.
iii. Vector A is used to find near and far fields of antennas.
C. Boundary conditions on magnetic fields : The magnetic field is continuous in a single medium. The boundary conditions for magnetic fields at a two-media interface can be found here.
i. Condition for normal component of magnetic field:
1. Let us consider two different media with permeabilities μ1 and μ2. Both media are linear, isotropic and homogenous.
2. In Fig., we have two different media with μ1 and μ2 respectively. We choose an elementary cylindrical Gaussian surface at the interface of two media so that half of cylinder is in media-1 and other half in media-2.
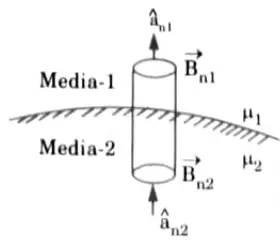


3. Now apply Gauss’s law for magnetic field.
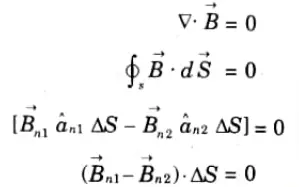
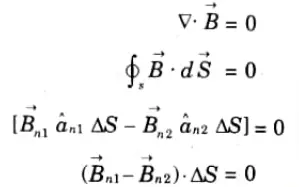
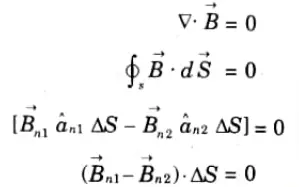



i.e., normal component of magnetic field intensity is discontinuous.
ii. Condition for tangential component of magnetic field:
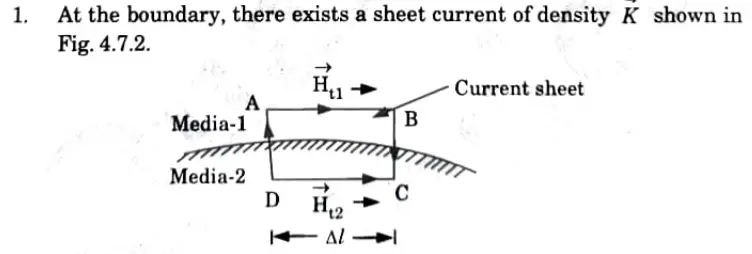


2. Apply Ampere’s circuital law,



3. Considering the closed path ABCD, we have
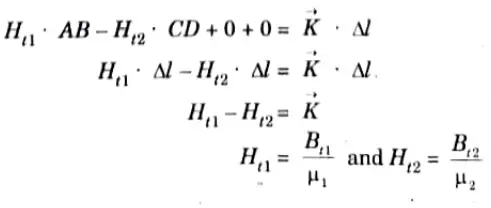
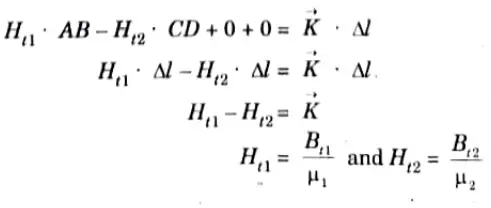
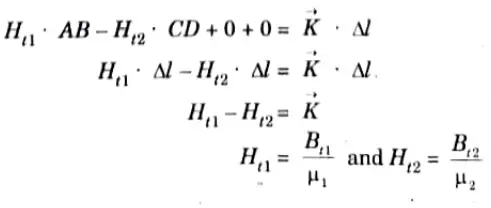



4. Tangential component of magnetic field intensity is discontinuous across the boundary and the value of discontinuity is equal to the surface current density (Vector k)
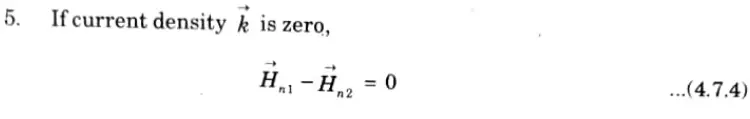
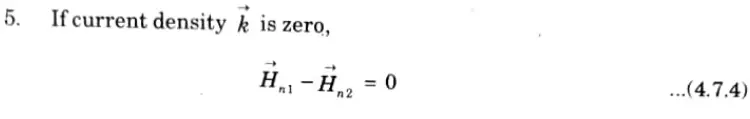
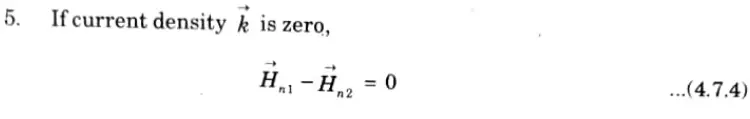
5. Thus, the tangential component of (Vector H) is continuous across the boundary between two media provided that the boundary has no current sheet
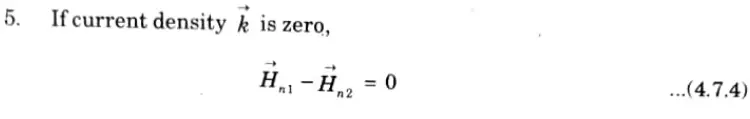
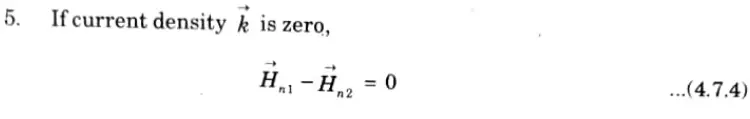
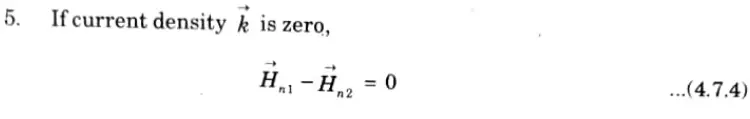
Section 6 Important Question
a. Explain transformer, and motional electromotive forces with necessary mathematical expressions. If vector A= yx2 ax + zx ay + xy az is expressed as, where ax, ay, and az are the unit vectors. Find the vector B.
Ans. A. Transformer emf(stationary loop in a time-varying
1. The emf induced by the time varying current (producing the time-varying ![]()
![]()
2. Let us consider a stationary conducting loop in a time-varying magnetic field ![]()
![]()
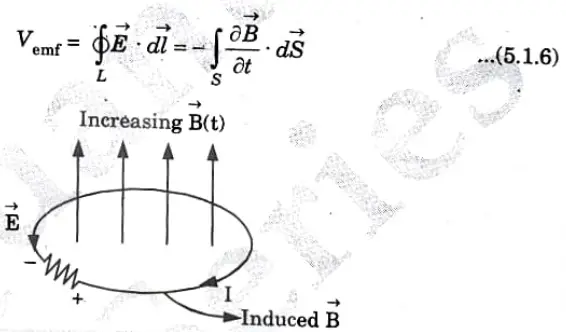


3. By applying Stoke’s theorem to the middle term in eq., we get
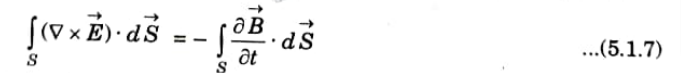
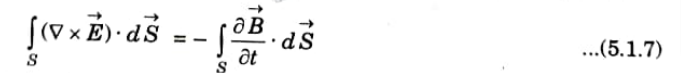
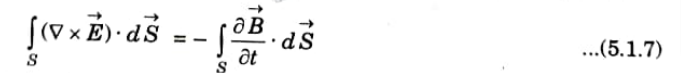
For the two integrals to be equal, their integrands must be equal,



B. Motional emf (moving loop in a static Vector B field):
1. When a conducting loop is moving in a static Vector B field, an emf is induced
in the loop. The force on a charge moving with uniform velocity Vector u in a magnetic field Vector B is given by
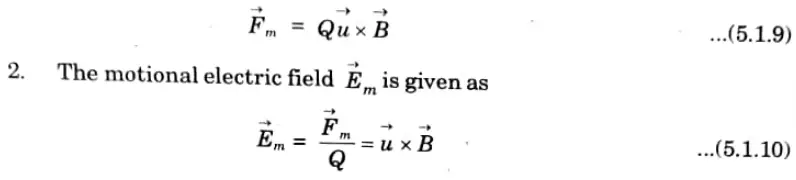
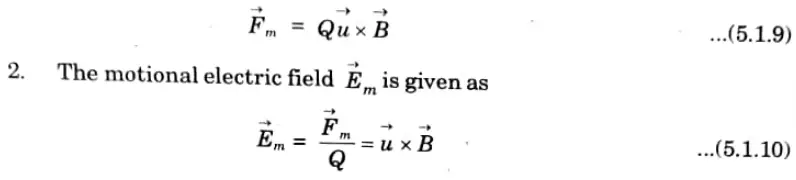
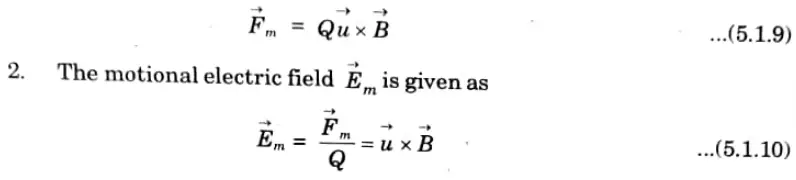
3. If a conducting loop is considered moving with uniform velocity Vector u, consisting of large number of free electrons, the emf induced in the loop is
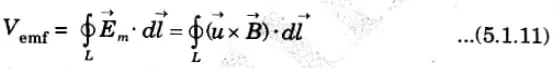
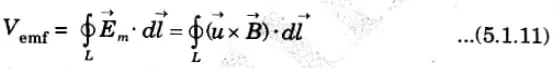
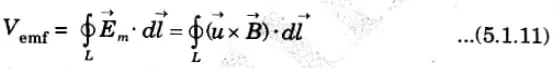
4. Because it results from motional activity, this sort of emf is known as motional emf. Electric devices including motors, generators, and alternators produce this type of emf.
C. The given numerical part is incomplete.
b. A charged particle of mass 2 kg and charge 3 C starts at point (1, – 2, 0) with velocity 4 a, +3 a, m/s in an electric field 12 a+ 10a, Vim. At time t = 1 sec, determine the acceleration of the particle, its velocity, kinetic energy of the particles and its position.
Ans. 1. According to Newton’s second law of motion,
F = ma = QE
where, a is the acceleration of the particle. Hence,
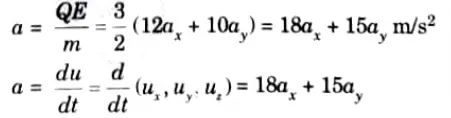
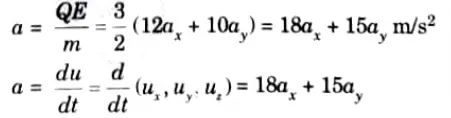
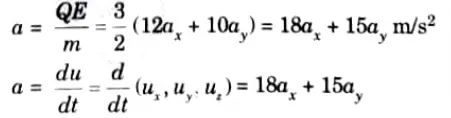
2. Equating components and then integrating, we obtain






7. Equating components yields
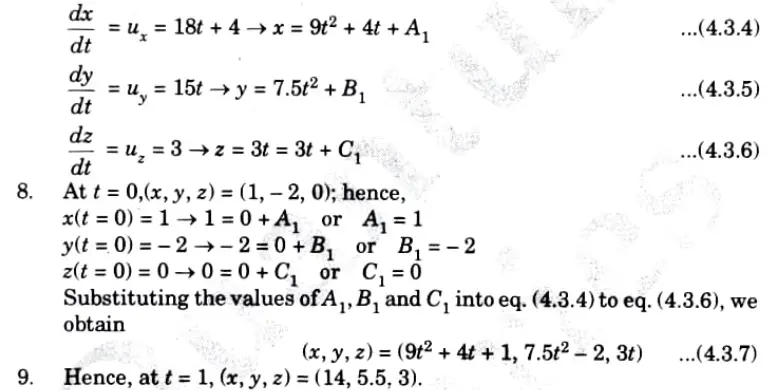
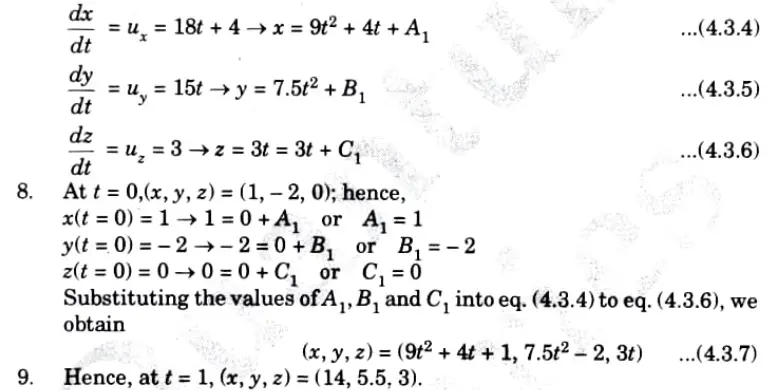
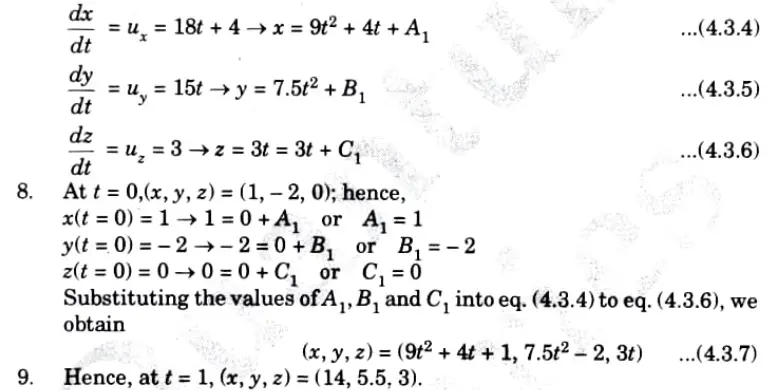
10. By eliminating t in eq. (4.3.7), the motion of the particle may be described in terms of x, y and z.
Section 7 Important Question
a. Explain uniform plane wave. Derive uniform plane waves in lossless dielectrics. What is skin effect? Explain the smith chart in detail.
Ans. A. Uniform plane wave : When the electric and magnetic fields are measured, a uniform plane wave is created. The directions of the electric and magnetic fields are orthogonal.
B. Uniform plane wave in lossless dielectrics:



C. Skin effect:
1. The depth at which a wave attenuates to 1/e of its original amplitude is known as the depth of penetration. Skin depth is another name for penetration depth.
2. It is a measure of depth to which an electromagnetic wave can penetrate the medium.
3. The depth of penetration,
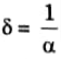
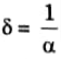
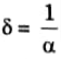
where, α = Attenuation constant.
4. The skin effect is a phenomena whereby the field intensity in a conductor rapidly drops.
5. Higher resistance is caused by the propensity of charges to migrate from the bulk of conducting material to the surface.
D. Smith chart:
1. It is a graphical method used for solving lossless transmission line problems.
2. It consists of a collection of concentric circles, or circles that represent continuous conductance and resistance.
3. This chart comprises of the values of impedance and admittance in the normalized form. Normalized impedance:
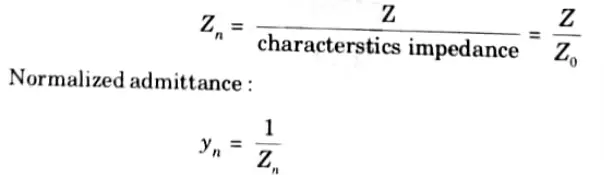
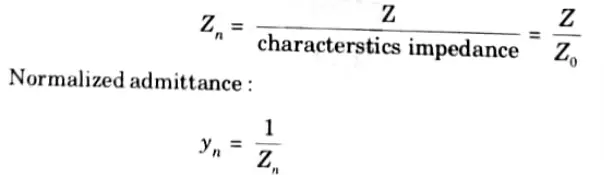
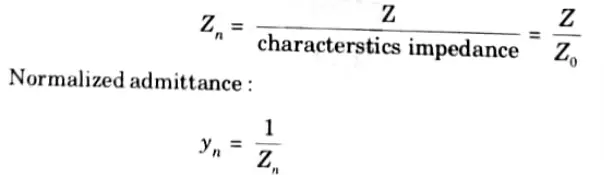
Drawing of Smith chart:
1. The Smith chart is a graphical means of obtaining line characteristics such as Γ, s and Zin. It is constructed within a circle of unit radius |Γ| ≤ 1) as shown in Fig.
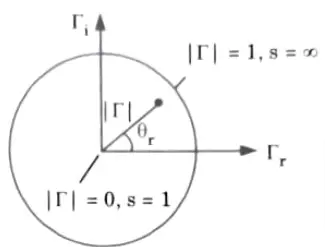


2. The construction of chart is based on a relation as



5. Equating real and imaginary components of eq. (5.27.5), we get



6. Rearranging terms in eq. (5.27.6) and (5.27.7) leads to
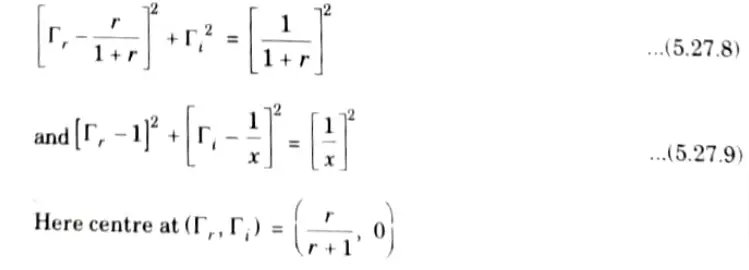
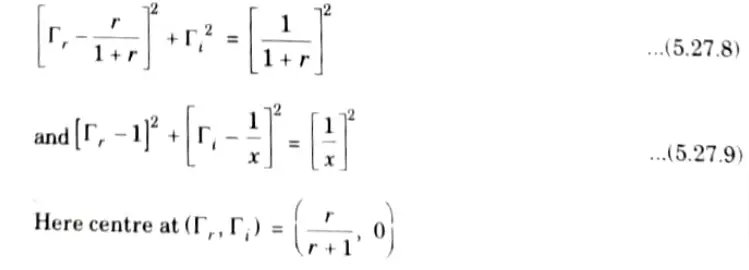
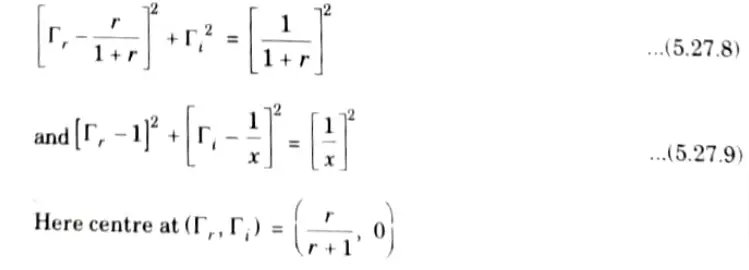
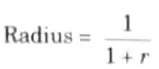
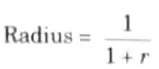
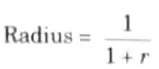
7. There are two explicit circles (the reactance and resistance circles) and one implicit circle for each r and x. (the constant s-circle).
b. What is transmission line ? Derive all the supporting mathematical equations of the transmission line.
Ans. A. Transmission line : Information can be transferred from one location to another using a transmission line. It typically has two conductors. It serves as the link between a source and a load. The load could be a receiver, while the supply could be a transmitter.
B. Expression of voltage and current in a transmission line:
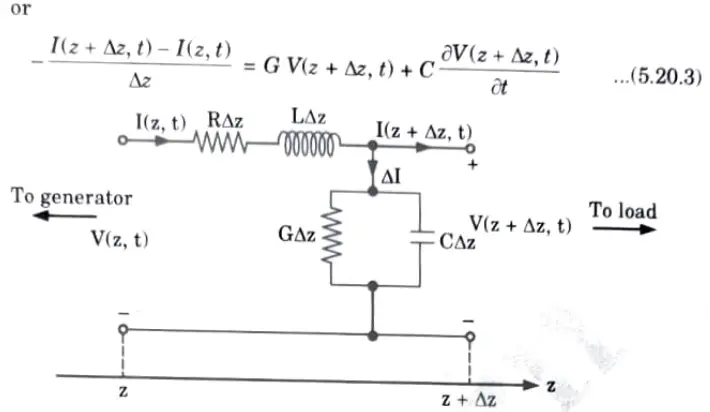
1. By applying Kirchhoff’s voltage law to the outer loop of the circuit in Fig. 5.20.1, we obtain
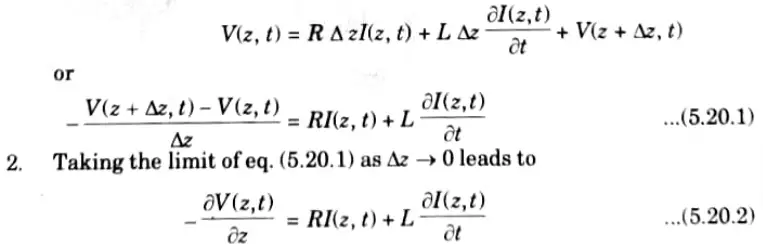
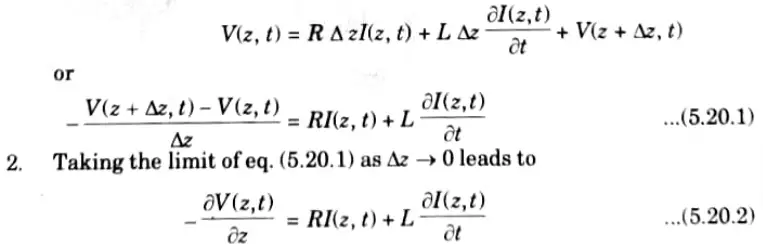
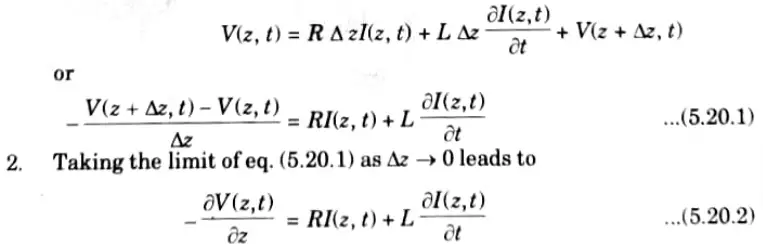
3 Similarly, applying Kirchhoff’s current law to the main node of the circuit in Fig. 5.20.1 gives
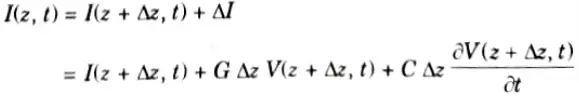
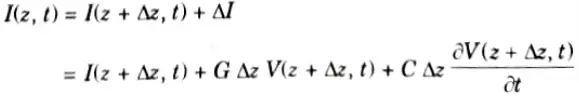
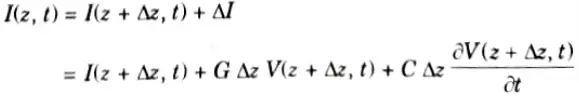














Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Electromagnetic Field Theory Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Electromagnetic Field Theory Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
Important Links-Btech (AKTU)
