AKTU Btech Unit 01 COORDINATE SYSTEMS covers numerous coordinate systems, transformations, vector operations, and their applications in geometry, physics, and engineering. Improve spatial representation and problem-solving abilities.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Electromagnetic Field Theory: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. What is a dot product ?.Also mention its properties and applications.
Ans. A. Scalar (or Dot) product:
1. The scalar or dot product of the two vectors A and B (you can take reference from image how to write vector A and B) is defined as the product of the magnitude of vector A, the magnitude of vector B and the cosine of the smaller angle between them.
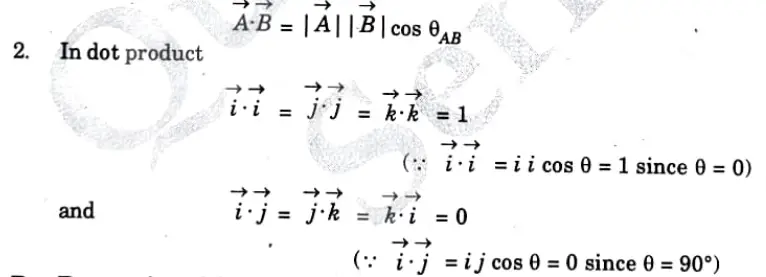
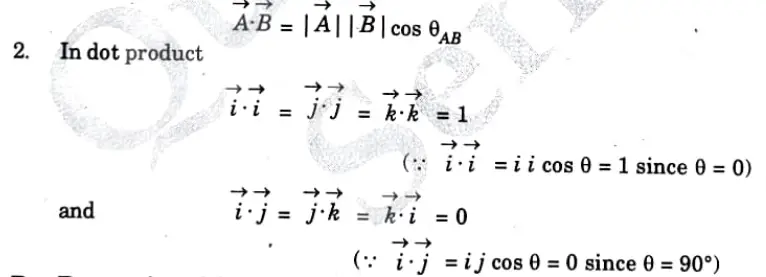
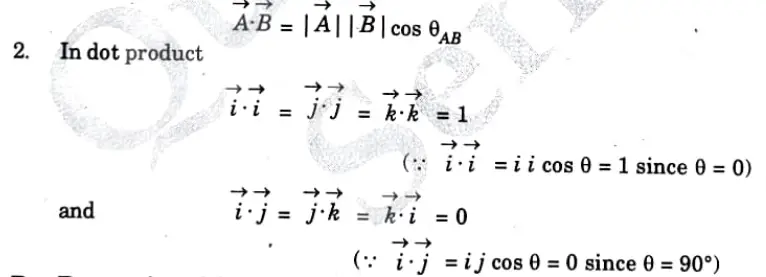
B. Properties of dot product:
1. If the two vectors are parallel to each other, i.e. 𝝷 = 0° then cos 𝝷AB =1



C. Applications of dot product:
1. To find the angle between the two vectors.
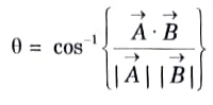


3. Physically, work done by a constant force Vector F over a straight displacement Vector d can be expressed as a dot product of two vectors.
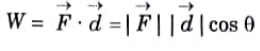
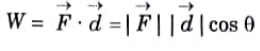
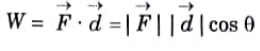
Q2. What is a cross product ? Also mention its properties.
Ans. A. Cross (or vector) product:
1. The cross or vector product is defined as the product of the magnitudes of vectors A and B (you can take reference from image how to write vector A and B) and the sine of the smaller angle between vectors A and B But this product is a vector quantity and has a direction perpendicular to the plane containing the two vector vectors A and B .
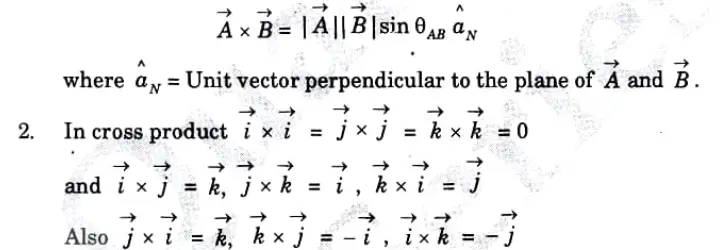
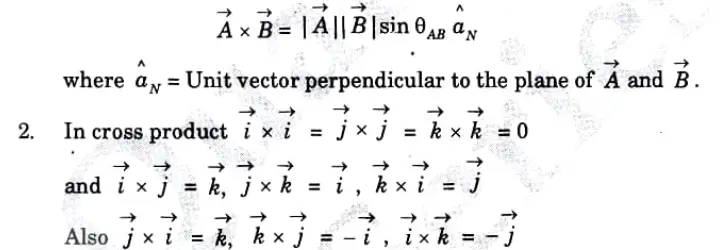
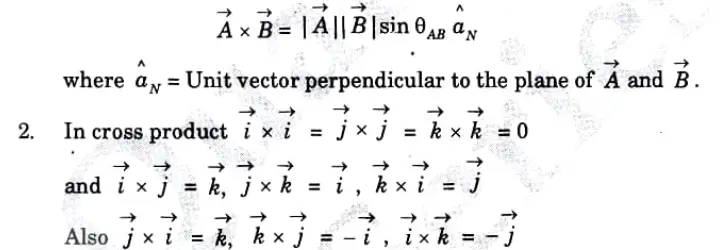
B. Properties of cross product:
1. Two vectors are considered parallel if their cross product is zero.
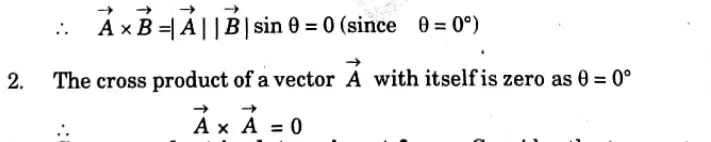
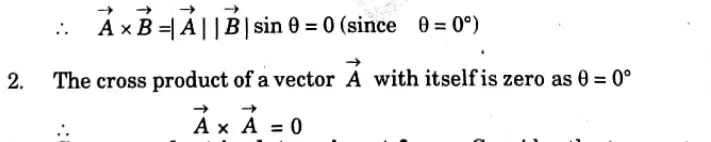
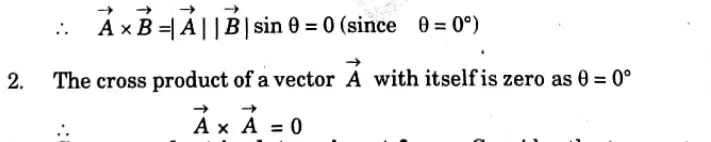
3. Cross product in determinant form: Consider the two vector in the cartesian system as,
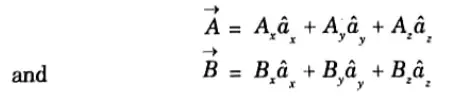
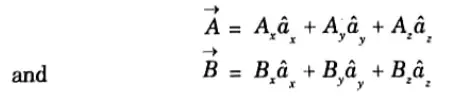
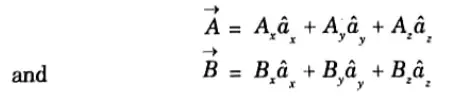
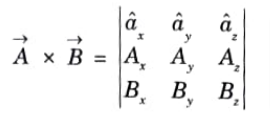
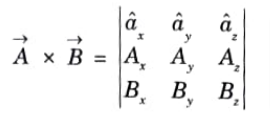
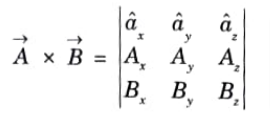
Q3. Write a short note on cartesian coordinate system.
Ans. 1. It is also known as rectangular coordinate system.
2. In rectangular coordinate system, three coordinate axis, i.e., x, y and z are set up mutually at right angles to each other.
3. A point Pin cartesian coordinate system is represented by P(x,y,z).
4 The ranges of the coordinate variables x, y and z are



Q4. Give a brief description on cylindrical coordinate system ?
Ans. A. Cylindrical coordinate system:
1. A point P (ρ, ф, z) in cylindrical coordinate system represents p the radius of the cylinder, ф the azimuthal angle and z is same as in cartesian system.
2. The ranges of variables ρ, ф and z are
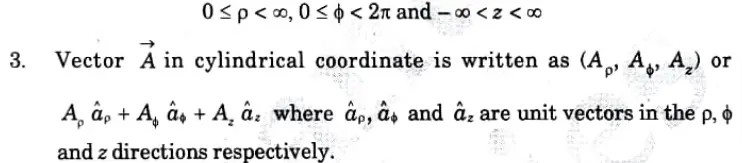
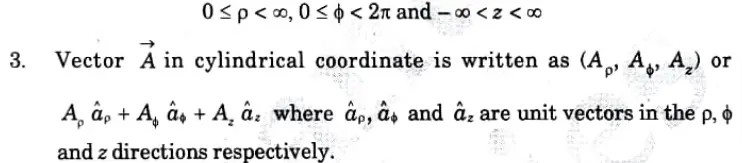
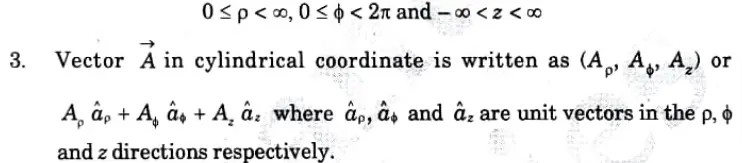
B. Relation between cartesian and cylindrical ocoordinate system:



Q5. Convert a point P(4, -3, 6) and a vector R = z ax + y az into cylindrical coordinate systems.
Ans. 1. At point P, x = 4, y =-3, 2 = 6
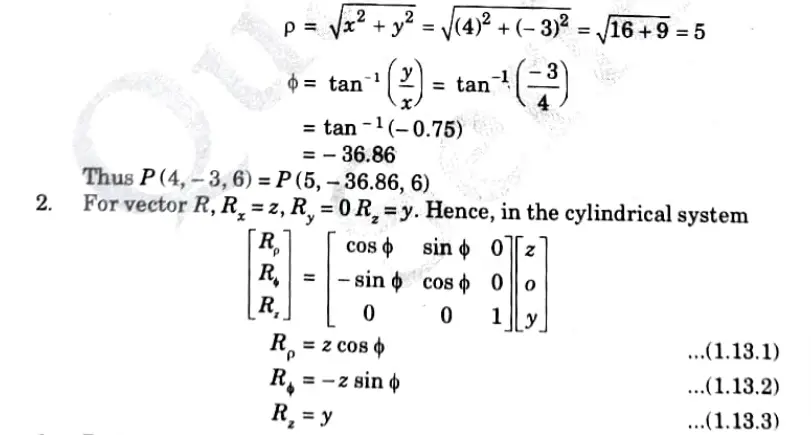
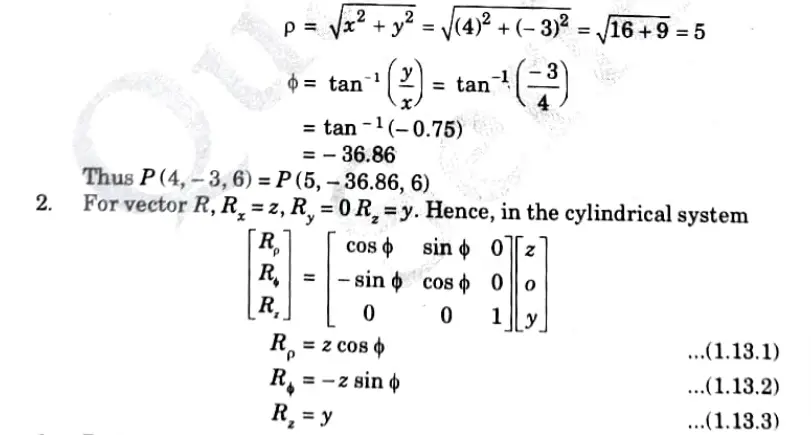
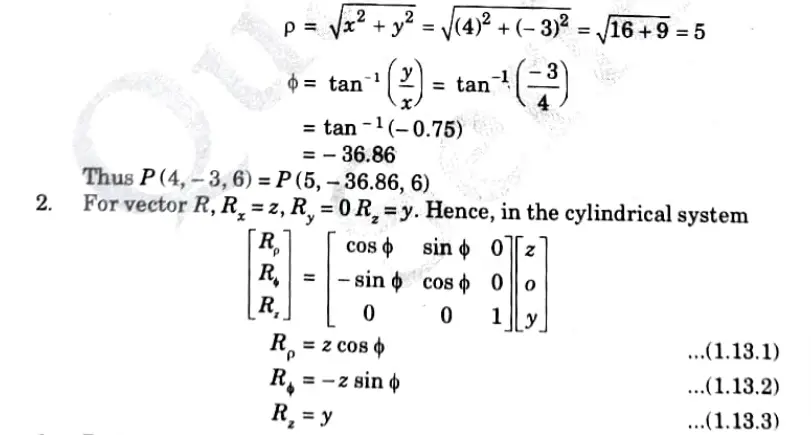
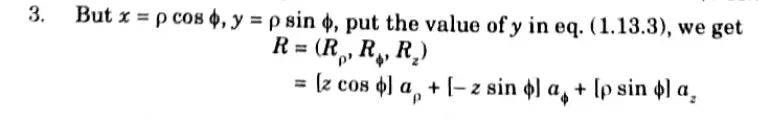
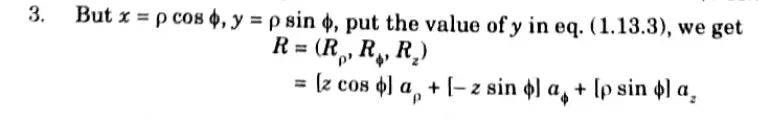
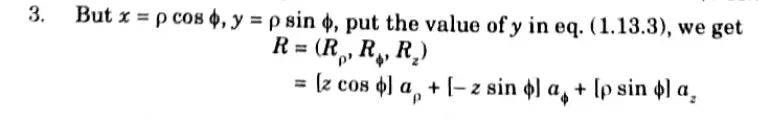
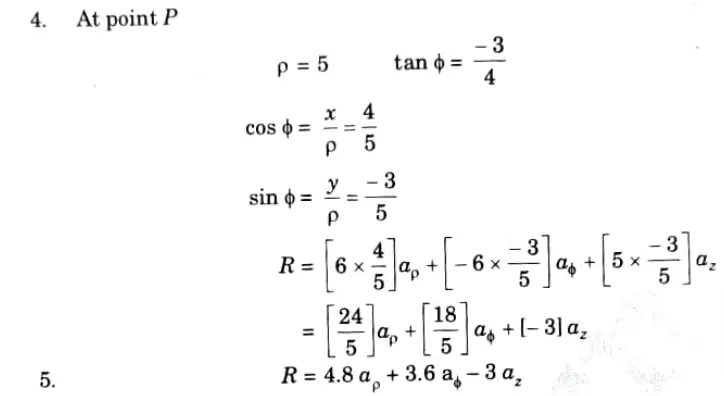
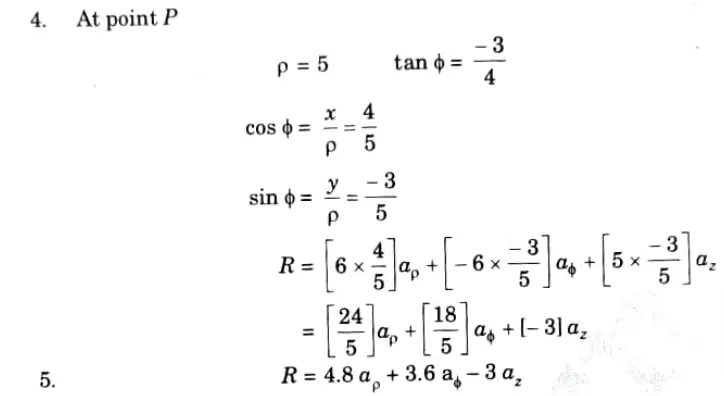
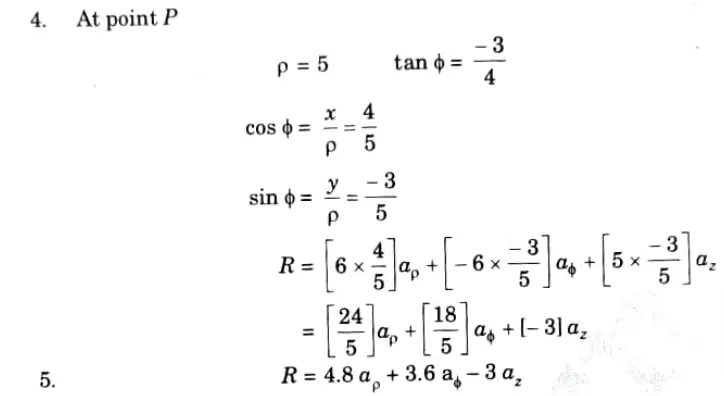
Q6. Describe the gradient of a scalar field.
Ans. A. Gradient of scalar field:
1. The gradient of a scalar field M is a vector that depicts the maximum rate of increase of M in space in terms of both magnitude and direction.
2. The operation of the ▽(del) operator on a scalar function is called gradient of a scalar



B. Properties of gradient of scalar:
- 1. The gradient ▽M gives the maximum rate of change of M per unit distance.
- 2. The gradient ▽M always indicates the direction of the maximum rate of change of M.
- 3.The gradient ▽M at any point is perpendicular to the constant M surface, which passes through the point.
- 4. The directional derivative of M along the unit vector a is ▽M. a , which is projection of ▽M in the direction of unit vector a.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Electromagnetic Field Theory Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Electromagnetic Field Theory Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
Important Links-Btech (AKTU)

5 thoughts on “Unit 01 COORDINATE SYSTEMS Important Question Answer AKTU Btech”