Unit 05 of Electromagnetic Field Theory delves into waves and their practical applications. Propagation, equations, polarization, reflection, refraction, transmission lines, antennas, and wave interactions with structures are among the topics covered. Students learn about waveguides, microwave circuits, wireless communication, and optical fibers.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Electromagnetic Field Theory: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. Explain the concept of displacement current in an electrical circuit. Also determine the condition when conduction current becomes equal to displacement current.
Ans. A. Displacement current:
1. Let’s think about Maxwell’s curl equation for magnetic fields under time-varying conditions in order to comprehend the idea of displacement current.
2. Thus, for static EM fields,



Taking the divergence of each side of eq. (5.2.1)
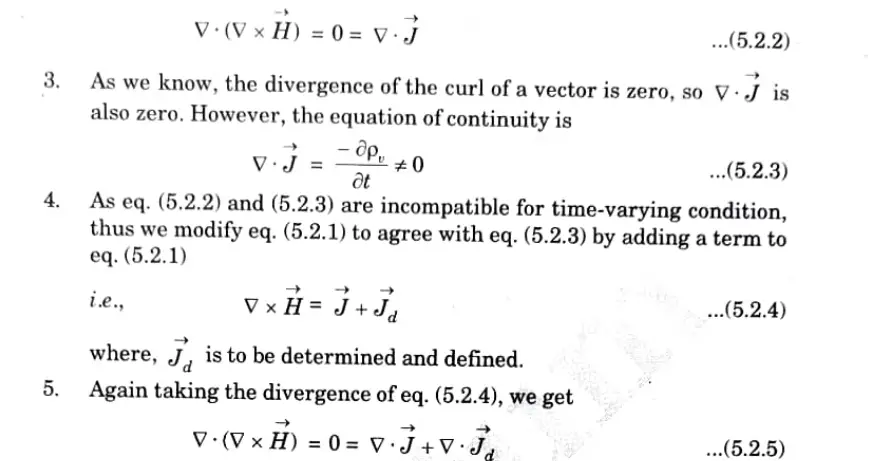
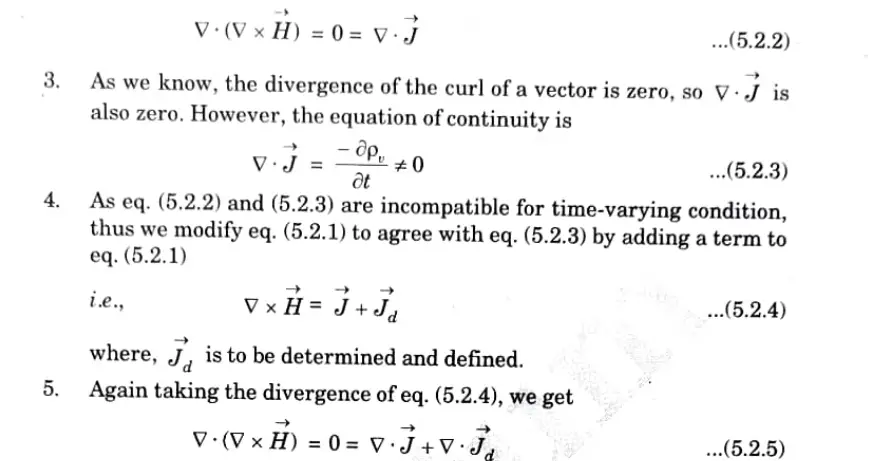
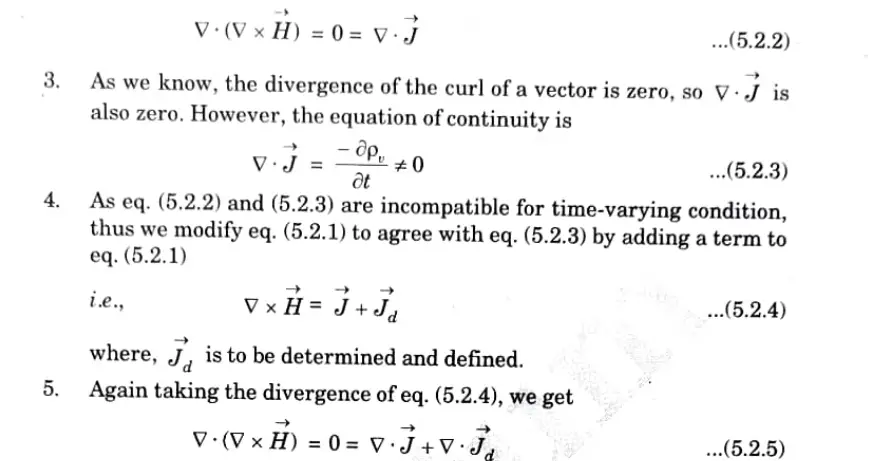



B. Condition: Conduction current is equal to the displacement current in the capacitor’s gap between the plates when it is charged.
Q2. What do you mean by lossy dielectric and explain the wave propagation in lossy dielectric.
Ans. It is a medium where an EM wave loses power as it travels due to a defective dielectric.
2. A lossy dielectric is a partially conducting medium (imperfect dielectric or imperfect conductor) with σ ≠ 0.
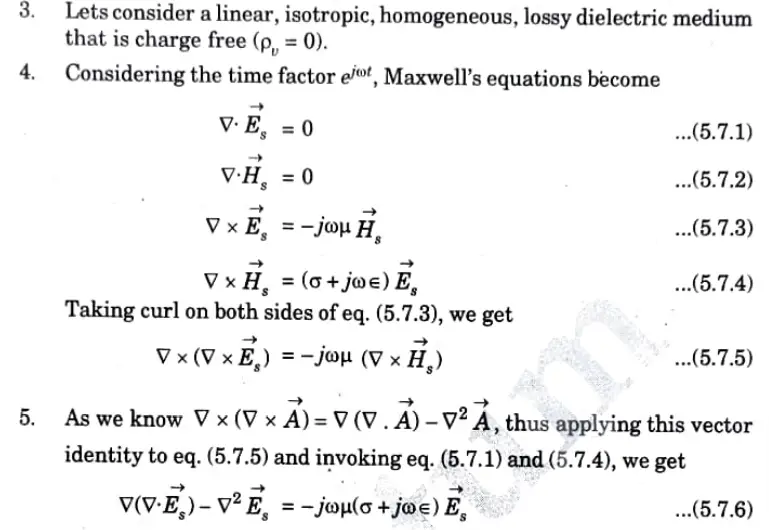
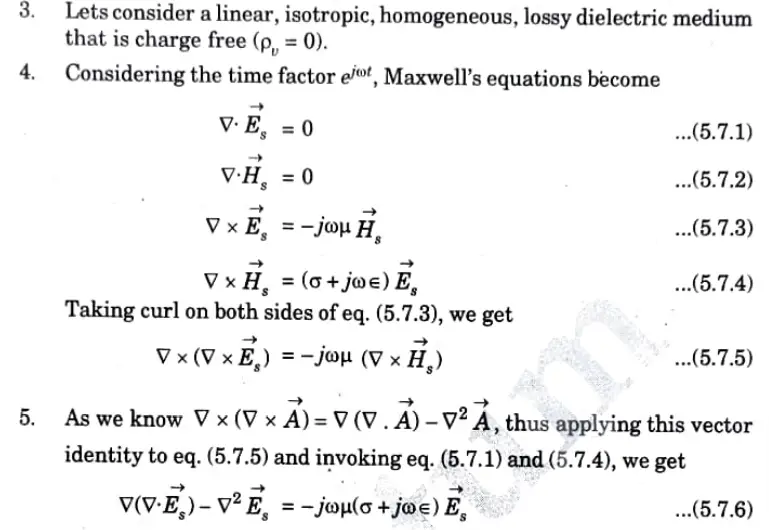
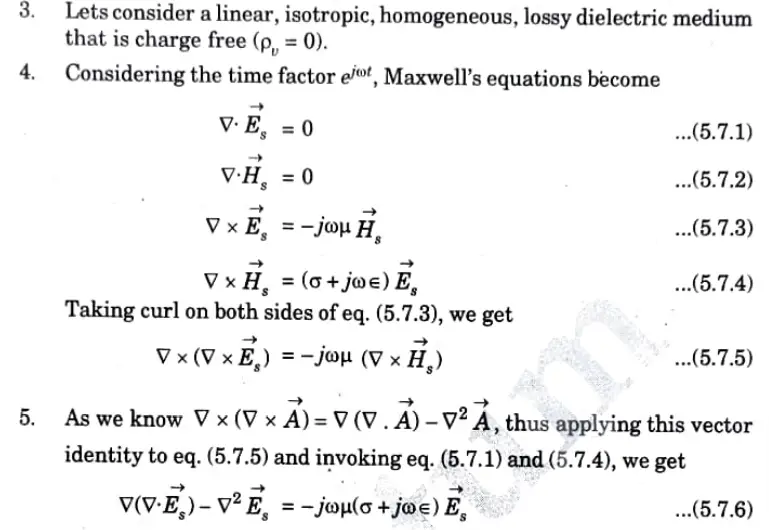



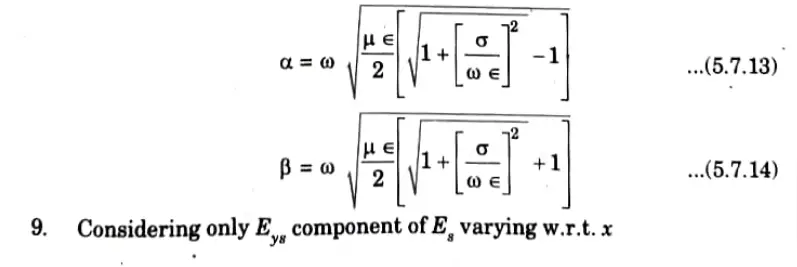





Q3. Discuss the propagation of plane waves in
- i. Lossless dielectrics
- ii. Free space
- iii. Good conductors.
Ans. i. Lossless dielectric:



ii. Free space:
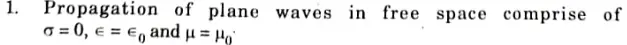
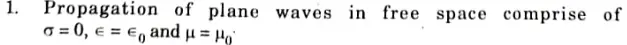
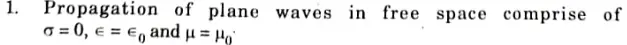



iii. Good conductor:



Q4. A 10 GHz plane wave travelling in free space has an amplitude of Ex = 10 V/m. Find v, η, β, λ and the amplitude of H.
Ans. Given: Ex = 10 V/m andf= 10 GHz
To Find:v, η, β, λ, H
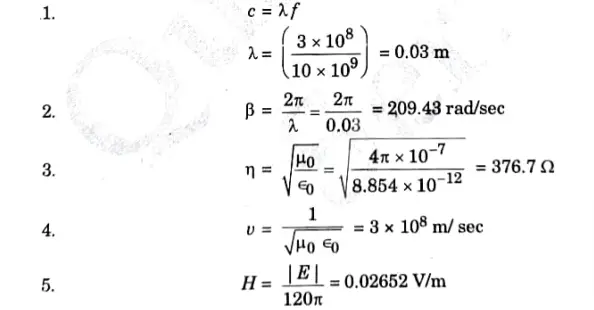
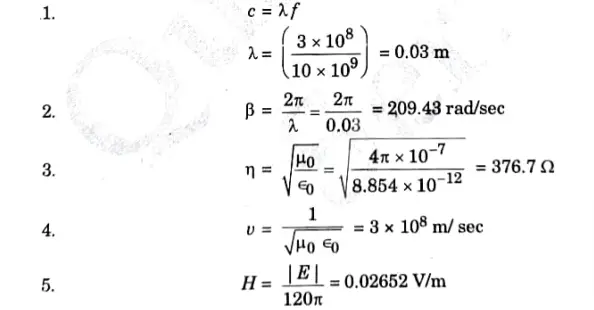
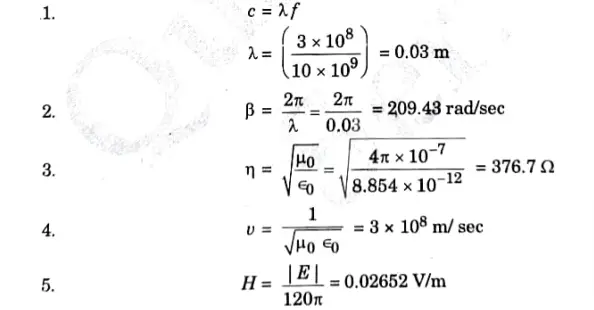
Q5. Explain Poynting vector. Derive an expression of Poynting theorem for EM wave. Also explain the significance of each term of the expression.
Ans. 1. Energy can be transported from one point to another point by means of EM waves. The rate of such energy transportation can be obtained from Maxwell’s equations:



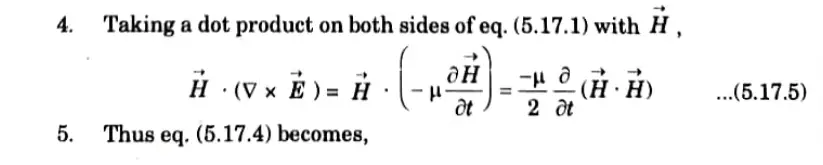
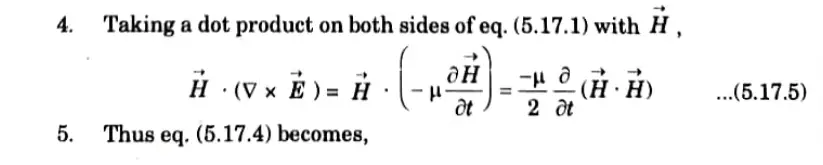
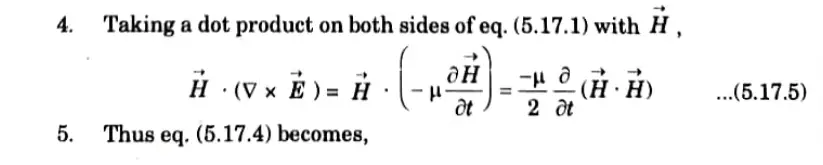



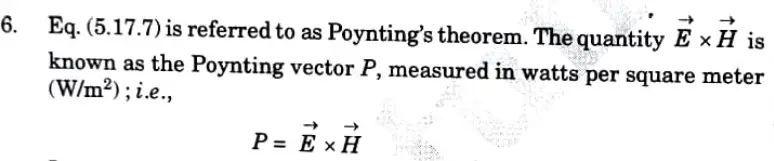
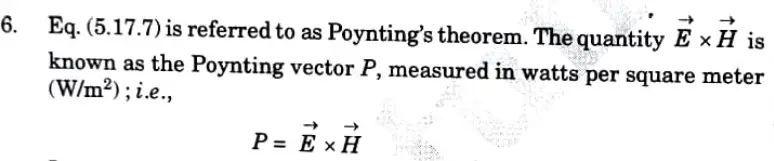
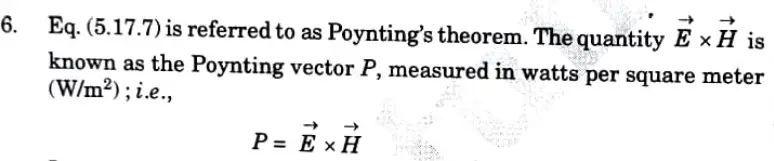
It represents the instantaneous power density vector associated with the EM field at a given point.
7. Any closed surface’s net power flowing out can be calculated by integrating the Poynting vector over that surface.
8. According to the Poynting theorem, the net power leaving a given volume U is equal to the rate at which the energy stored there is vanishing over time minus any Ohmic losses.
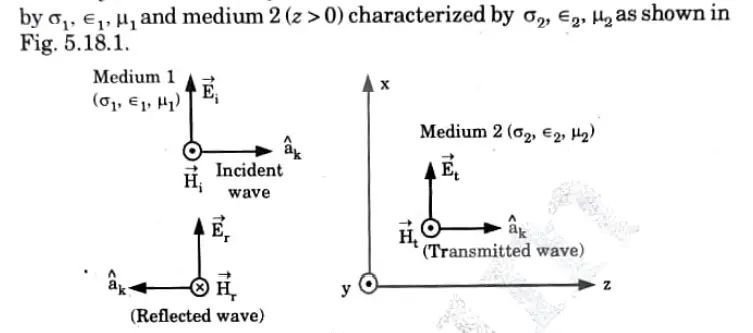
Q6. Explain the reflection of plane wave for the normal incidence. Discuss about reflection and transmission coefficient for E and H.
Ans. 1. If load impedance (ZL) is not equal to characteristic impedance (Zo) mismatch then occurs. In this case the part of the wave gets absorbed by the load while the rest part is reflected back to the source. Thus, due to mismatch in impedance the reflection occurs.
2. Suppose that a plane wave propagating along +z direction incident normally on the boundary z = 0 between medium 1(z< 0) characterized


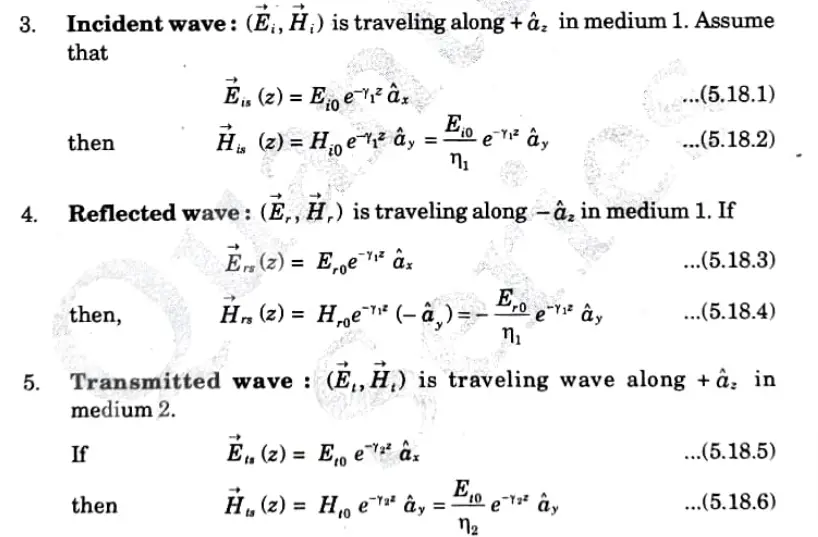
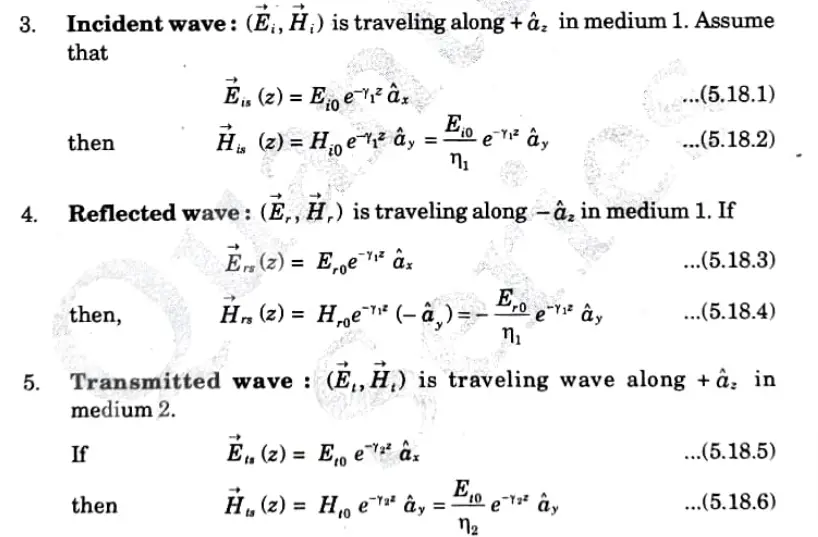
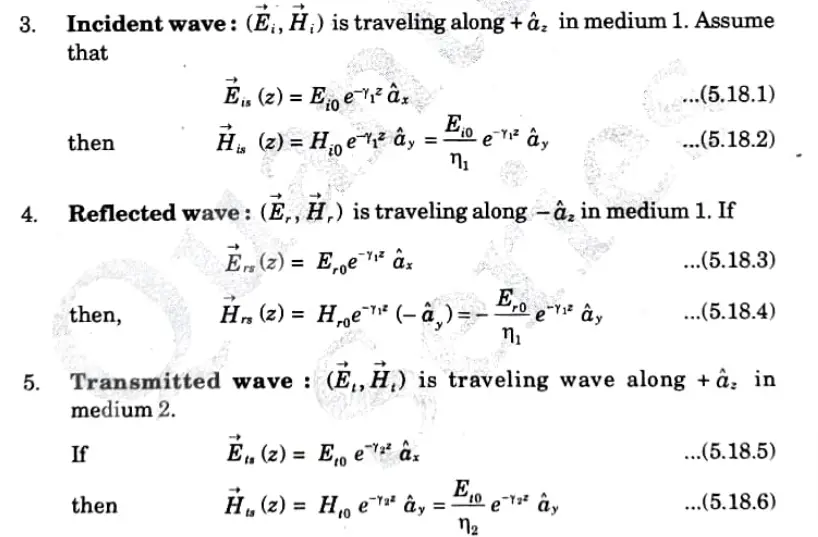









Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Electromagnetic Field Theory Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Electromagnetic Field Theory Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
Important Links-Btech (AKTU)
