Basic Structural Analysis is covered in Unit 03 of Engineering Mechanics. This lesson is vital for students who desire to work in structural engineering or a related field. Students will study about the behavior of various structural components under various sorts of loads in this subject.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Engineering Mechanics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. What are the different types of frames ?
Ans. Following are the different types of frames:
i. Perfect Frame:
1. The term “perfect frame” refers to a frame made up of such components that are merely necessary to maintain the frame’s balance while it is bearing the weight of an external load.
2. For a perfect frame, the number of joints and number of members are given by,
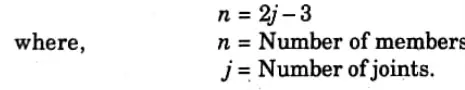
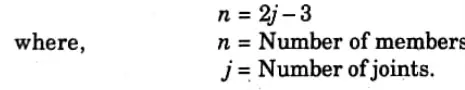
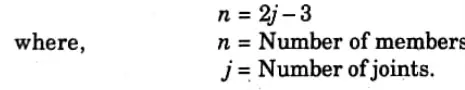
ii. Imperfect Frame:
1. Imperfect frames are those in which the number of members and the number of joints do not follow the formula n = 2j – 3. Therefore, the number of members in a flawed frame will either be more or (2j – 3).
2. A frame is referred to be a deficient frame if there are fewer members than (2j – 3).
3. If the number of members in a frame are more than (2j- 3), then the frame is known as redundant frame.
Q2. Find forces in the members EC, FC and FD of the truss shown in Fig.
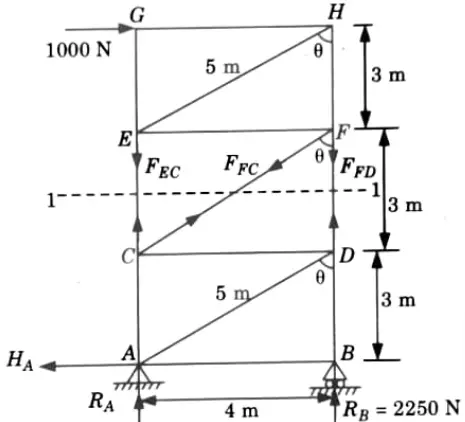


Ans. Given: Fig.
To Find: Forces in the members EC, FC and FD
1. From geometry of Fig.
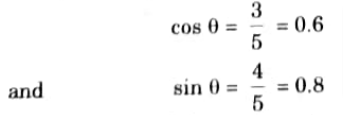
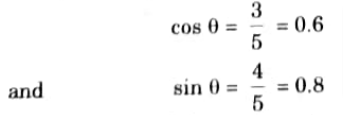
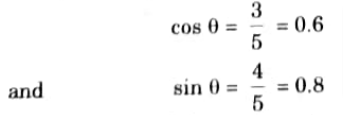
2. Draw the FBD of the portion above section 1 – 1 (Fig.)
3. Consider the equilibrium of the FBD of the drawn portion,
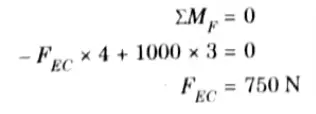
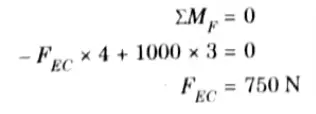
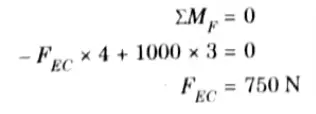
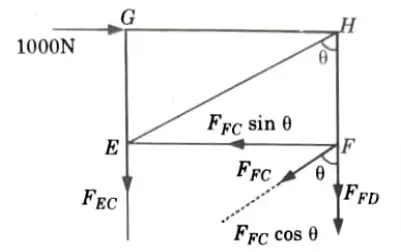


4. Consider the condition of equilibrium at point F,
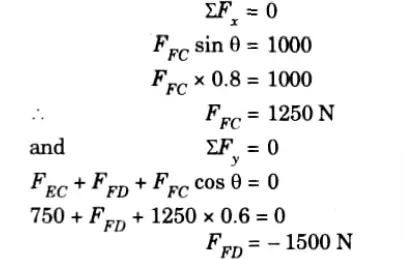
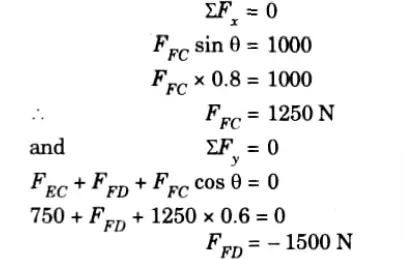
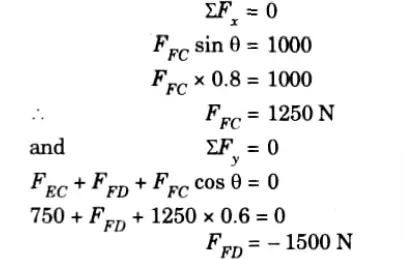
5. So, direction of FFD is opposite to our assumed direction hence it is compressive in nature.
Q3. Write a short note on zero force members.
Ans. 1. Zero force members are the members in which there is no force.
2. Once the members of zero forces are known, they can be removed from the calculation of the members’ forces.
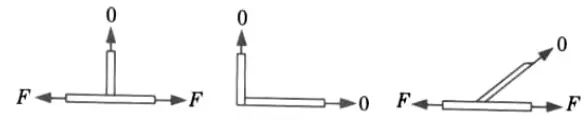


3. A member with the shapes of a “L,” “T,” and “Y” that joins two additional collinear members at right angles will be a zero force member if no load is acting at that joint.
Q4. What are the different types of beams ?
Ans. Following are the different types of beams:
i. Cantilever Beam:
- 1. Cantilever beams are beams that are fixed at one end and free at the other (Fig.)
- 2. There will be a fixing moment at the fixed end. Depending on the kind of load occurring on the beam, there may also be horizontal and vertical reactions at the fixed end.



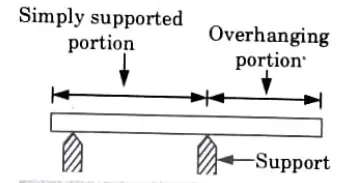
ii. Simply Supported Beam: The term “supported beam” refers to a beam that is either supported or rests freely on supports at both ends (Fig.)



iii. Overhanging Beam: The term “overhanging beam” refers to a beam whose terminal section extends beyond the support (Fig.)


iv. Fixed Beam: A fixed beam is one that has both of its ends fastened to the ground or integrated into walls (Fig. ). A built-in or encastre beam is another name for a fixed beam. There will be reactions and fixing moments at the fixed ends.


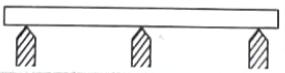
v. Continuous Beam: A continuous beam is one that has more than two supports, like in the illustration.


Q5. Determine the reactions at A for the cantilever beam subjected to the distributed and concentrated loads Fig.
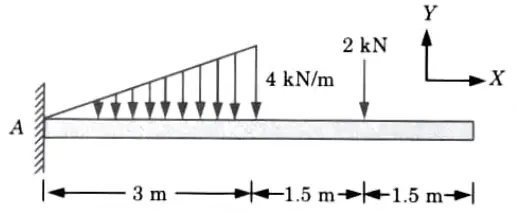


Ans. Given: Fig.
To Find: Reaction at A.
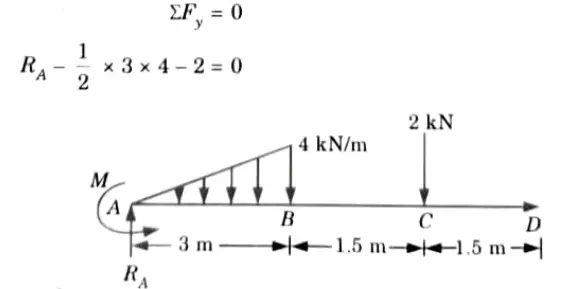
1. Consider the equilibrium of the beam,





Q6. Write the procedure of method of section in truss analysis.
Ans. Procedure of method of sections is as follows:
Step1: The truss is split into two parts by passing an imaginary section.
Step2: The fictitious section needs to be designed so that it only splits three of the members into which the forces are to be calculated.
Step3: The conditions of equilibrium ΣFx = 0, ΣFy =0, and ΣM = 0 are applied for one part of the truss and the unknown forces in the member is determined.
Step4: Any member’s type of force is arbitrarily chosen to be either tensile or compressive when studying equilibrium.
i. If a force’s magnitude is positive, its direction can be assumed to be in the right direction.
ii. The actual force’s direction is the reverse of what has been expected, though, if the force’s magnitude turns out to be negative.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Engineering Mechanics Quantum, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Engineering Mechanics Quantum PDF: | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |

2 thoughts on “Unit 03 Basic Structural Analysis In Engineering Mechanics”