Discover the enthralling world of PROPOSITIONAL & PREDICATE LOGIC Unit 04 for Btech AKTU’s Discrete Structure. In this thrilling unit, dive into truth tables, logical connectives, quantifiers, and formal proofs to become a master of logical reasoning!
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Discrete Structures and Theory of Logics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. Define the term proposition. Also, explain compound proposition with example.
Ans. Proposition: A proposition is a statement that can only be either true or wrong. It is a declarative statement. It is usually denoted by lower case letters P, g, r, s, t etc. They are called Boolean variable or logic variable.
For example:
1. Dr.A.P.J. Abdul Kalam was Prime Minister of India.
2. Roses are red.
3. Delhi is in India (1) proposition is false whereas (2) and (3) are true.
Compound proposition: Two or more separate propositions, known as components or sub-propositions, combine to make a compound proposition.
For example:
1. Risabh is intelligent and he studies hard.
2. Sky is blue and clouds are white.
Here, the first statement makes the claims that Risabh is intelligent and that he studies diligently, whereas the second statement makes the claims that the sky is blue and the clouds are white. because two propositions are used to produce both claims. They are compound propositions as a result.
Q2. Explain the following terms with suitable example:
- i. Conjunction
- ii. Disjunction
- iii. Conditional
- iv. Converse
- v. Contrapositive
Ans. i. Conjunction:
If p and q are two statements, then conjunction of p and q is the compound statement denoted by p ⋀ g and read as “p and q”. Its truth table is,



Example:
p: Ram is healthy.
q: He has blue eyes.
p ⋀ q: Ram is healthy and he has blue eyes.
ii. Disjunction: If p and q are two statements, the disjunction of p and q is the compound statement denoted by p V q and it is read as “p or q”. Its truth table is,
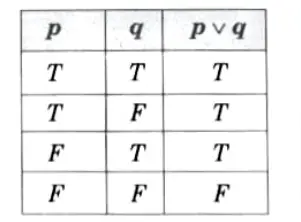


Example:
p: Ram will go to Delhi.
q: Ram will go to Calcutta.
p V q: Ram will go to Delhi or Calcutta.
iii. Conditional: If p and q are propositions. The compound proposition if p then q denoted by p >q or p → q and is called conditional proposition or implication. It is read as “If p then q” and its truth table is,
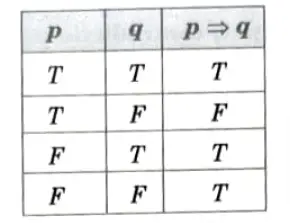


Example :
p: Ram works hard.
g: He will get good marks.
P → q: If Ram works hard then he will get good marks.
For converse and contrapositive:
Let p: It rains.
q: The crops will grow.



Q3. Explain tautologies, contradictions, satisfiability and contingency.
Ans. 1. Tautology : Tautology is defined as a compound proposition that is always true for all possible truth values of its propositional variables and it contains T in last column of its truth table.
Propositions like,
- i. The doctor is either male or female.
- ii. Either it is raining or not.
are always true and are tautologies.
2. Contradiction: Contradiction is defined as a compound statement that contains the letter F in the last column of its truth table and is always untrue for all possible values of its propositional variables.
Propositions like,
- i. x is even and x is odd number.
- ii. Tom is good boy and Tom is bad boy.
are always false and are contradiction.
3. Contingency: Contingency is the definition of a statement that is neither a tautology nor a contradiction.
Here the last column of truth table contains both T and F.
4 Satisfiability: A compound statement formula A (P1, P2, … Pn) is said to be satisfiable, ifit has the truth value T for at least one combination of truth value of P1, P2, … Pn.
Q4. Write short note on algebra of propositions.
Ans. Proposition satisfies various laws which are useful in simplifying complex expressions. These laws are listed as :






These laws can easily be verified using truth table.
Q5. “If the labour market is perfect then the wages of all persons in a particular employment will be equal. But it is always the case that wages for such persons are not equal therefore the labour market is not perfect”. Test the validity of this argument using truth table.
Ans.
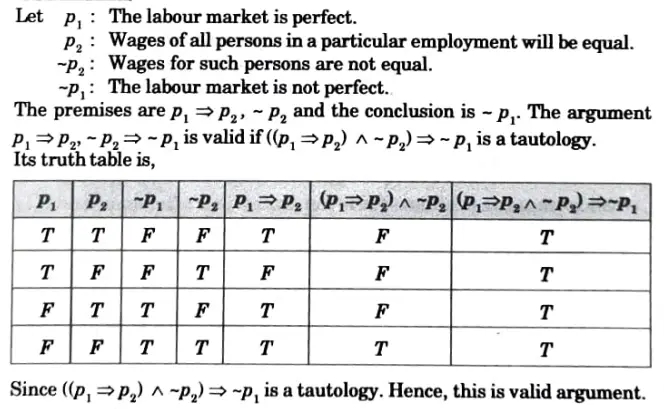


Q6. Write the symbolic form and negate the following statements:
- a. Everyone who is healthy can do all kinds of work.
- b. Some people are not admired by everyone.
- c. Everyone should help his neighbours, or his neighbours will not help him.
Ans.






Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Discrete Structures and Theory of Logics Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Discrete Structures and Theory of Logics Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
