Hello, there! This site is jam-packed with fast questions for Discrete structures and theory of logics, a course in AKTU Btech. You’ll learn about amazing ideas like logic, sets, functions, relations, combinatorics, and graphs. It’s a helpful resource that can help you ace those examinations or refresh your recollection on the course’s important themes. Enjoy!
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Discrete Structures and Theory of Logics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. What do you understand by partition of a set ?
Ans. A partition of a set A is a collection of non-empty subsets A1, A2,……… An called blocks, such that each element ofA is in exactly one of the blocks. i.e.,



Q2. Define transitive closure with suitable example.
Ans. The transitive closure of the relation is the relation to which the fewest ordered pairs are added to guarantee transitivity. R* stands for the transitive closure of R.
Q3. Let R be a relation on the set of natural numbers N, as R={(a,y) :x,y ∊N, 3x + y = 19)} Find the domain and range of R. Verify whether R is reflexive.
Ans. By definition of relation,
R = {(1, 16), (2, 13), (3, 10), (4, 7), (5, 4), (6, 1)}
∴ Domain = {1, 2, 3, 4, 5, 6}
∴ Range = {16, 13, 10, 7,4, 1}
R is not reflexive since (1, 1) ∉ R.
Q4. Show that the relation R on the set Z of integers given by R={(a, b):3 divides a – b}, is an equivalence relation.
Ans. Reflexive: a – a = 0 is divided by 3
∴ (a,a) ∊ R ∀ a ∊ Z
∴ R is reflexive.
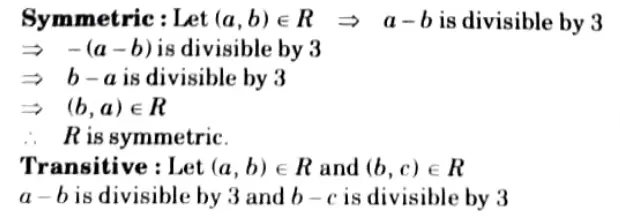
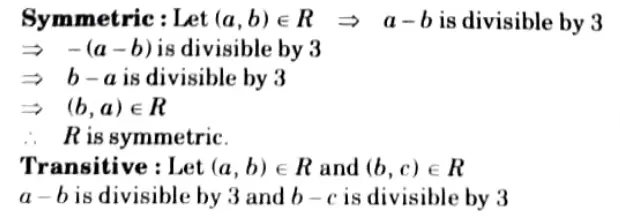
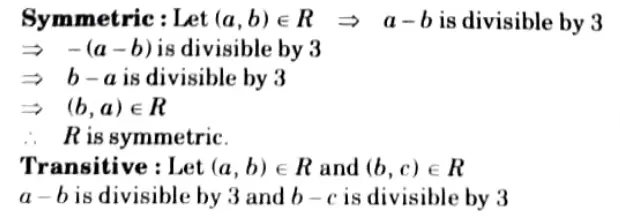
Then a -b + b-cis divisible by 3
a – c is divisible by 3
∴ (a,c) ∊ R
∴ Ris transitive.
Hence, R is equivalence relation.
Q5. Mention some properties of cartesian product.
Ans. For the four sets A, B, C and D
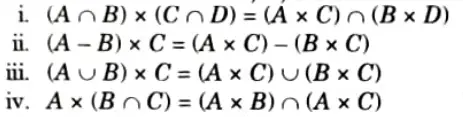
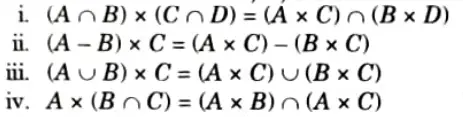
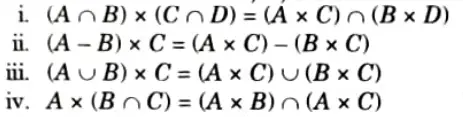
Q6. Discuss countable and uncountable sets.
Ans. A set is considered countable if it is either empty, finite, or countably infinite; otherwise, it is considered uncountable. As a result, if P is a one-to-one function from N onto A, then A is countable.
Q7. Write a short note on composition of relation.
Ans. The composite of, say R and S denoted by RoS, is the relation consisting of ordered pairs (a, c) when a ∊ A and c ∊ C, and for which there exists an element b ∊ B such that (a, b) ∊ R and (b, c) ∊ S.
Q8. How many symmetric and reflexive binary relations are possible on a set S with cardinality n ?
Ans. There are 2n(n + 1)/2 symmetric binary relations and 2n(n-1) reflexive binary relations are possible on a set S with cardinality.
Q9. Let A= {a, {a}}. Determine whether the following statements are true or false:
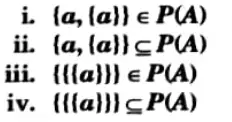
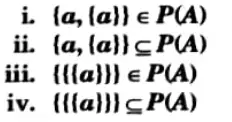
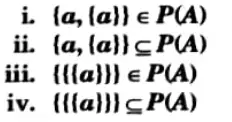
Ans. i. False: {a, {a}} is not an element of A.
ii True: {a,{a}} is a subset of A.
iii. False: {{{a}}} is not an element of A.
iv. False: {{{a}}} is a subset of A.
Q10. Find out the cardinality of the following sets :
A = {x : x is weeks in a leap year}
B = {x 😡 is a positive divisor of 24 and not equal to zero}
C = {{{}}}
D = {{Ø,{Ø}}}
Ans. i. We know that there are 52 weeks in a leap year.
∴ The cardinality of A is 52.
ii. The positive divisors of 24 are 1,2,3,4, 6, 8, 12, 24.
∴ |B|= 8
iii. The set C has only one element.
∴ |C| = 1
iv. The set D has only one element.
∴ |D| = 1
Q11. If the function f : R →R defined by f(x) = x2, find f1 (4) and f-1 (-4).
Ans.
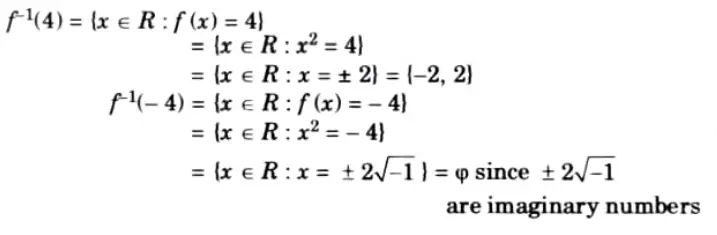
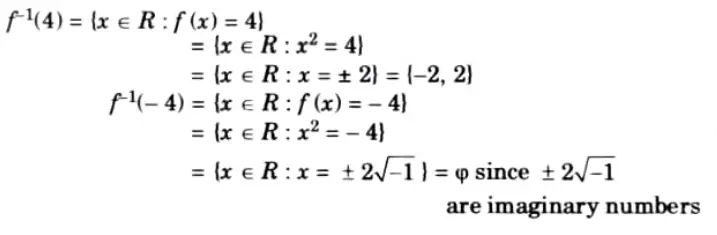
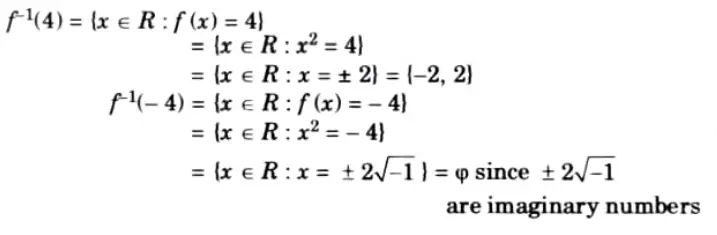
Q12. Show that if set A has 3 elements, then we can have 26 symmetric relations on A.
Ans. Number of elements in set = 3
Number of symmetric relations if number of elements is n = 2n(n+1)/2
Here, n = 3
∴ Number of symmetric relations
= 23(3+1)/2
= 23(4)/2.
= 26
Hence proved.
Q13. If f : A → B is one-to-one onto mapping, then prove that
f-1 : B → A will be one-to-one onto mapping.
Ans.
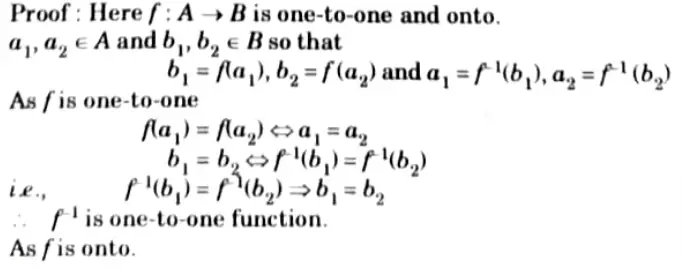
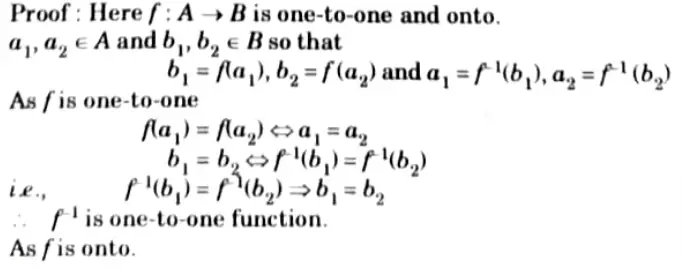
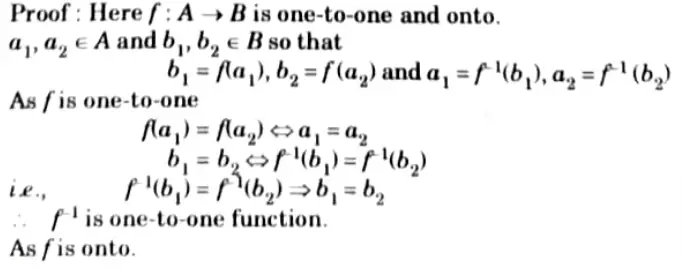
Every element of B is associated with a unique element of A i.e., for any a ∊ A is pre-image of some b ∊ B where b = f(a) → a = f-1 (b) i.e., for b ∊ B, there exists f image a ∊ A.
Hence,f-1 is onto.
Q14. Define multiset and power set. Determine the power set A = {1,2}.
Ans. Multiset: Multisets are sets where an element can occur as a member more than once. For example: A = {p, p, p, q, q, q, r, r, r, r}
B= {p, p, q, q, q, r}
are multisets.
Power set: A power set is a set of all subsets of the set.
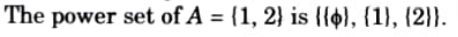
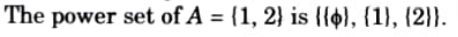
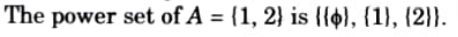
Q15. Define cardinality.
Ans. The total number of items in a finite set is referred to as the set’s cardinality.
Q16. Define ordered pair.
Ans. A pair of things that have their components in a specific sequence are known as ordered pairs. The two parts are listed one after the other in the designated order, separated by a comma, and enclosed in parenthesis. The first component of the ordered pair (a, b) is referred to as a, and the second component as b.
Q17. Find the power set of each of these sets, where a and b are distinct elements.
i. {a}
ii. {a,b}
iii. {ф,{ф}}
Ans.
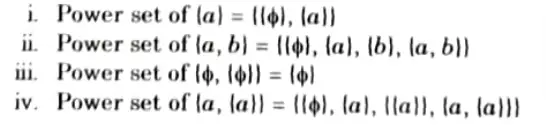
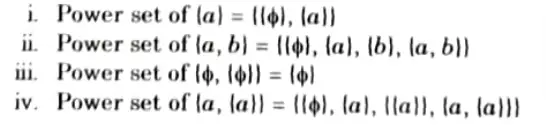
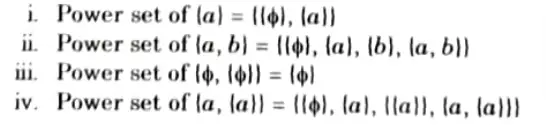
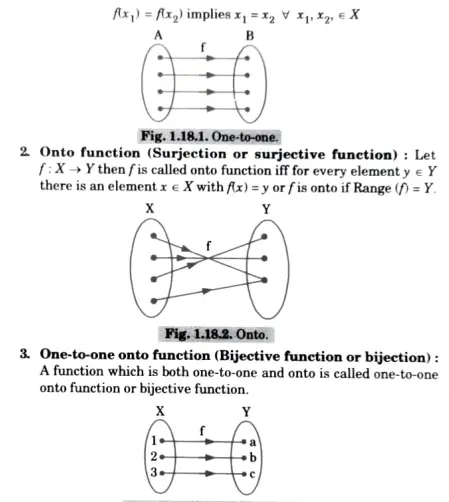
Q18. Define injective, surjective and bijective function.
Ans. 1. One-to-one function (Injective function or injection): Let f:X → Y then f is called one-to-one function if for distinct elements of X there are distinct image in Y i.e., f is one-to-one iff


Q19. Let A = (2, 4, 5, 7,8) = B, aRb if and only if a +b <= 12. Find relation matrix.
Ans.



Q20. Define union and intersection of multiset and find for
A = [1, 1,4, 2, 2, 3], B = [1,2, 2,6,3,3]
Ans. Union: Let A and B be two multisets. Then, A ◡B, is the multiset where the multiplicity of an element in the maximum of its multiplicities in A and B.
Intersection: The intersection of A and B, A റ B, is the multiset where the multiplicity of an element is the minimum of its multiplicities in A and B.



Unit 2: Algebraic Structures
Q1. List the properties of cosets.
Ans. Let H be a subgroup of G and ‘a’ and 6 belong to G. Then,
- i. a ∈ aH
- ii. aH = H iff a ∈ H
- iii. aH = bH
- iv. aH = bH if f a-1 b ∈ H
Q2. List types of permutation group.
Ans. Types of permutation group are:
- i. Identity permutation
- ii. Inverse permutation
- iii. Cyclic permutation
- iv. Even and odd permutation
Q3. If a and b are any two elements of group G then prove (a * b)-1 = (b-1* a-l).
Ans. Consider (a*b) * (b-1*a-1)
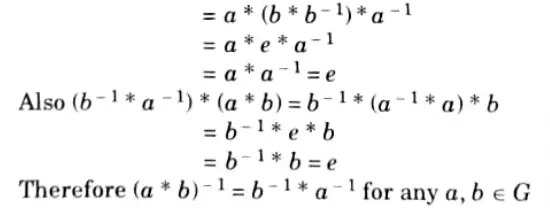
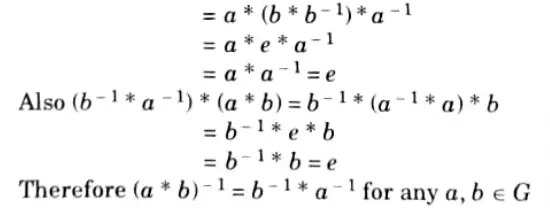
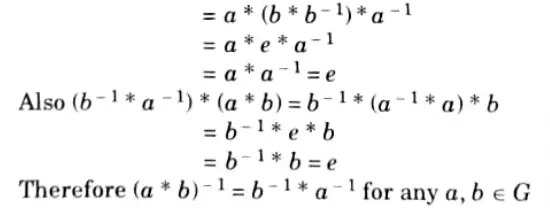
Q4. What do you mean by integral domain ?
Ans. A ring (R, +, .) is called an integral domain if,
- i. It is commutative.
- ii. It has multiplicative identity element.
- iii. It is without zero divisors.
Q5. Define ring and give an example of a ring with zero divisors.
Ans. Ring: A non-empty set R is a ring if it is equipped with two binary operations called addition and multiplication and denoted by ‘+’ and ‘.’ respectively i.e., for all a + b ∈ R we have a + b ∈ R and a.b ∈ R and it satisfies the following properties:



Q6. Prove that if a2=a, then a = e, a being an element of a group.
Ans. Let a be an element of a group G such that a2 = a
To prove that a = e.
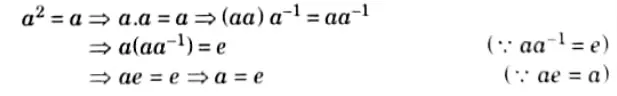
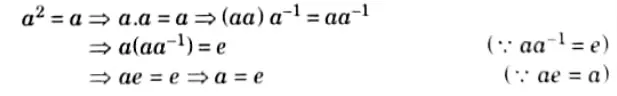
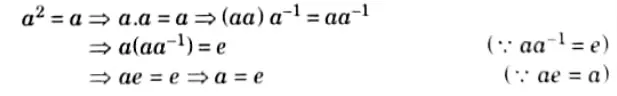
Q7. IfHis a subgroup of G such that a2 ∈ H for every x ∈ G, then prove that H is a normal subgroup of G.
Ans.



Q8. Prove that if a, b ∈ R then (a + b)2 =a2 + ab + ba + b2.
Ans. We have
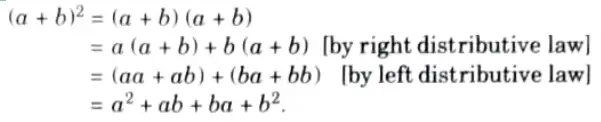
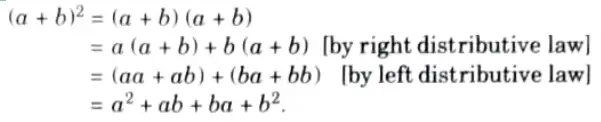
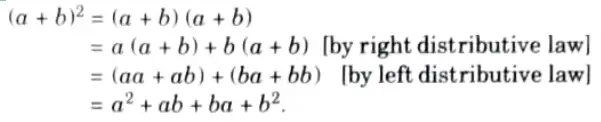
Q9. In an integral domain D, show that if ab = ac with a ≠ 0 then b = c.
Ans. Since ab = ac we have
ab – ac = 0 and so a(b-c) = 0
Since a ≠ 0, we must have b-c = 0, since D has no zero divisors.
Hence b = c.
Q10. Prove that left inverse of an element is also its right inverse i.e.,
a-1*a = e = a*a-1
Ans.
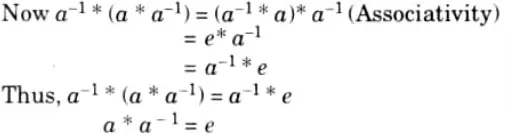
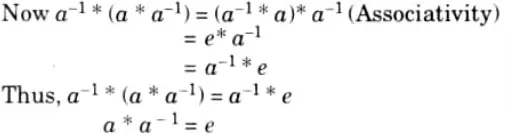
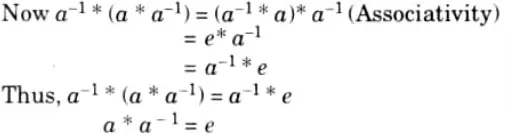
Thus, the left inverse of an element in a group is also its right inverse.
Q11. Define Lagrange’s theorem. What is the use of the theorem?
Ans. Lagrange’s theorem :
Statement: Each subgroup’s order in a finite group is divided by the group order.
Use of theorem:
- i. It can be used to find the subgroup of any order for the symmetric group.
- ii. It tells that the number of subgroups of the cyclic group of order p, when p is prime then there is only one subgroup and that is {ф}.
Unit – 3 (Lattices and Boolean Algebra)
Q1. Explain maximal and minimal element.
Ans. Maximal element: An element ‘a’ in the poset is called a maximal element of P if a ≤ x for no ‘x’ in P, that is, if no element of P strictly succeeds ‘a.
Minimal element: An element ‘b’ in P is called a minimal element of P if x ≤ b for no ‘x’ in P.
Q2. What do you mean by sublattice ?
Ans.



Q3. Write the following in DNF (x + y) (x’ +y’).
Ans.
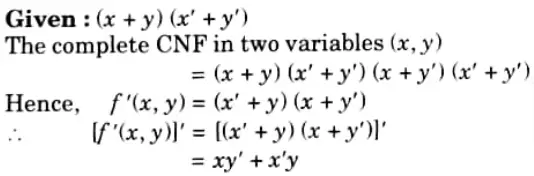
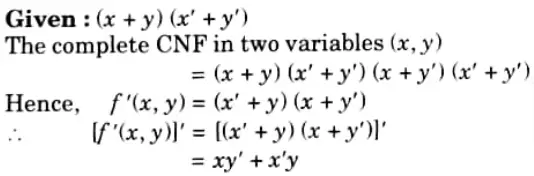
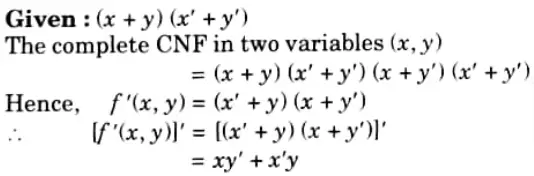
which is the required DNF.
Q4. Explain lattice homomorphism and lattice isomorphism.
Ans.



Q5. Define minterm and maxterm.
Ans. Minterm: A minterm of ‘n’ variables is a product of ‘n’ literals in which each variable appears exactly once in either true or complemented form, but not both.
Maxterm: A maxterm of ‘n’ variables is a sum of ‘n’ literals in which each variable appears exactly once in either true or complemented form, but not both.
Q6. Show that the relation ≥ is a partial ordering on the set of integers, Z.
Ans. Since:
- 1. a ≥ a for every a, 2 is reflexive.
- 2. a ≥b and b ≥ a imply a = b, 2 is antisymmetric.
- 3. a≥b and b≥c imply a ≥ c, 2 is transitive.
It follows that ≥ is a partial ordering on the set of integers and (Z, ≥) is a poset.
Q7. Consider A = {x ∈ R:1 <x < 21 with ≤ as the partial order.
Find
- i. All the upper and lower bounds of A
- ii. Greatest lower bound and least upper bound of A.
Ans.
- i. Every real number ≥ 2 is an upper bound of A and every real number ≤ 1 is a lower bound of A.
- ii. 1 is a greatest lower bound and 2 is the least upper bound of A.
Q8. Determine
- i. All maximal and minimal elements
- ii. Greatest and least element
- iii. Upper and lower bounds of ‘a’ and ‘b’, ‘c’ and ‘d’
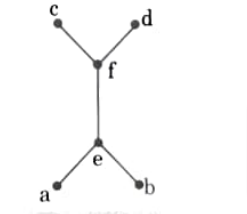


Ans.
- i. Maximal elements = c, d, Minimal element = a, b
- ii. Greatest and least elements do not exist.
- iii. Upper bound for a,b are e, f,c,d.
- Upper bound for c,d are does not exist.
- Lower bound for a,b are does not exist.
- Lower bound for e,d are f, e, a, b.
Q9. Let (A, ≤) be a distributive lattice. Show that if a Λ x = aΛy and a V x =a V y for some a then x = y.
Ans. We have x = x V(x Λ a) = x V (y Λ a) (∵ Given condition)
= (x V y) Λ (x V a)



Q10. Prove that (A + B) (A + C) = A+BC
Ans.
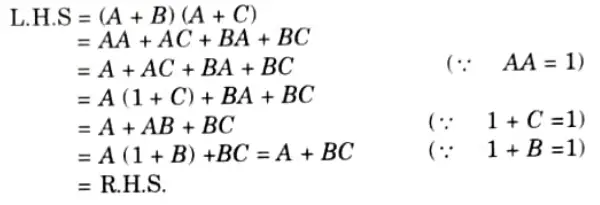
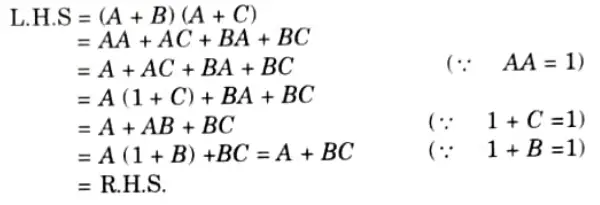
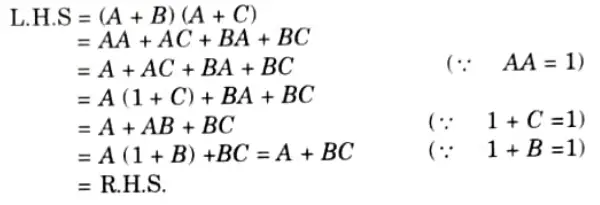
Q11. For a given function, F = xȳ+xȳ, find complement of F.
Ans.
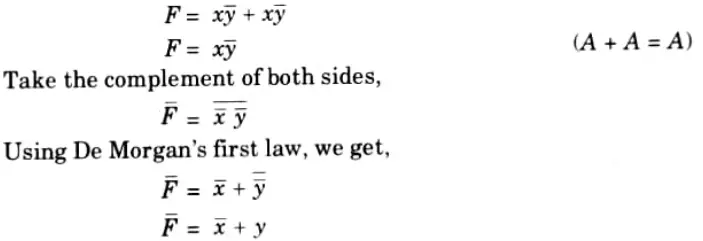
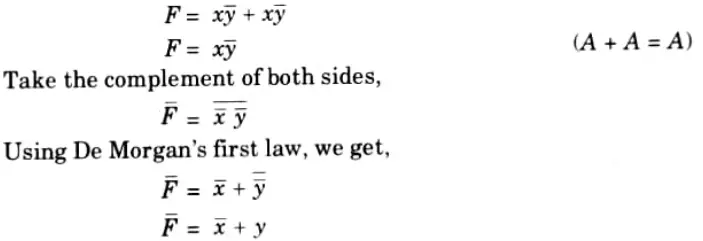
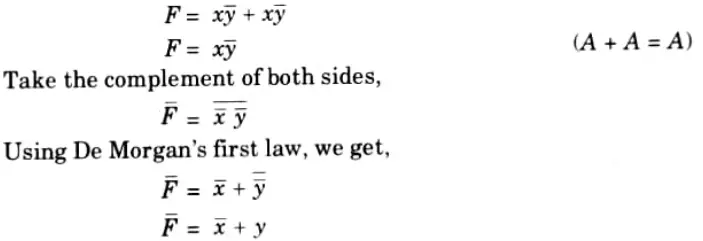
Q12. Obtain an equivalent expression for [(x. y) (z’ +xy’)].
Ans. Applying general form of De- Morgan’s theorem, we get
![Obtain an equivalent expression for [(x. y) (z' +xy’)]](https://bachelorexam.com/wp-content/uploads/2023/05/image-244.png)
![Obtain an equivalent expression for [(x. y) (z' +xy’)]](https://bachelorexam.com/wp-content/uploads/2023/05/image-244.png)
![Obtain an equivalent expression for [(x. y) (z' +xy’)]](https://bachelorexam.com/wp-content/uploads/2023/05/image-244.png)
Q13. Show that the “greater than or equal” relation (>=) is a partial ordering on the set of integers.
Ans.



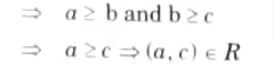
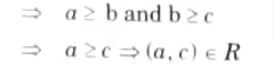
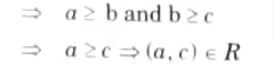
∴ R is transitive.
Hence, R is partial order relation.
Q14. Distinguish between bounded lattice and complemented lattice
Ans. Bounded lattice: A lattice which has both elements 0 and 1 is called a bounded lattice. Complemented lattice: A lattice L is called complemented lattice if it is bounded and if every element in L has complement.
Q15. Draw the Hasse diagram of D30.
Ans.
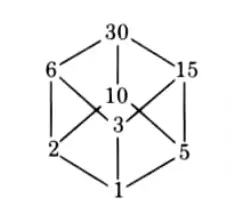


Q16. Define the terms: DNF and CNF.
Ans. Disjunction Normal Form (DNF) : If a logical expression is the join of elementary products, or the sum of elementary products, it is said to be in disjunction normal form.
Conjunctive Normal Form (CNF) : An expression is deemed to be conjunctive when it is logical. Standard Form Ifit is the result of simple calculations.
Unit – 4 (Propositional Logic and Predicate Logic)
Q1. What is compound proposition ?
Ans. A composite or compound proposition is one that was created by combining two or more assertions using logical operators or connectives of two or more propositions, or by negating a single proposition.
Q2. Show the implications without constructing the truth table (P → Q) Q ⇒ P ∨ Q.
Ans.



Q3. Prove that (P ∨ Q)→(P ⋀ Q) is logically equivalent to P ↔ Q.
Ans. (P ∨ Q)→(P ⋀ Q) = P ↔ Q



Q4. The converse of a statement is : If a steel rod is stretched, then it has been heated. Write the inverse of the statement.
Ans. The sentence “If a steel rod is stretched, then it has been heated” is the converse of the stated statement. What this means in reverse is that if a steel rod is not stretched, it has not been heated.
Q5. Give truth table for converse, contrapositive and inverse.
Ans. The truth table of the four propositions are as follows :
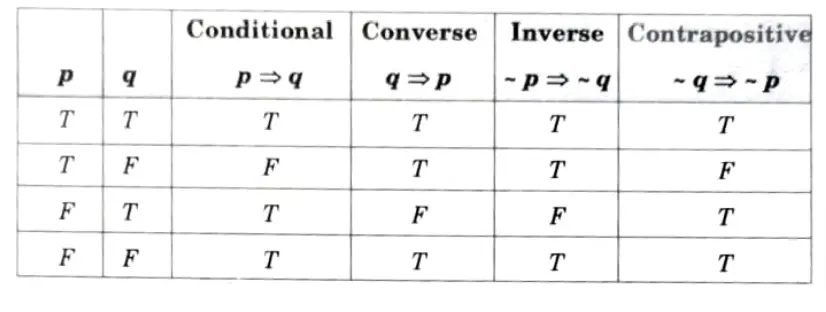


Q6. Show that contrapositive are logically equivalent; that is 〜q ⇒〜 p ≡ p ⇒ q.
Ans. The truth table of 〜q ⇒〜 p ≡ p ⇒ q are shown below and the logical equivalence is established by the last two columns of the table, which are identical.



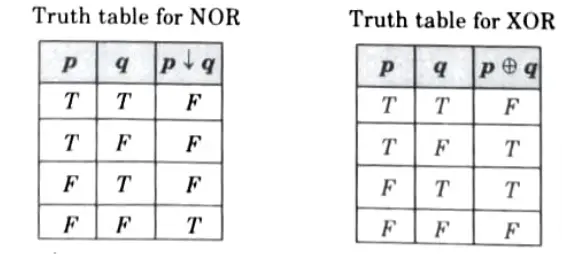
Q7. Give truth table for NOR and XOR.
Ans.


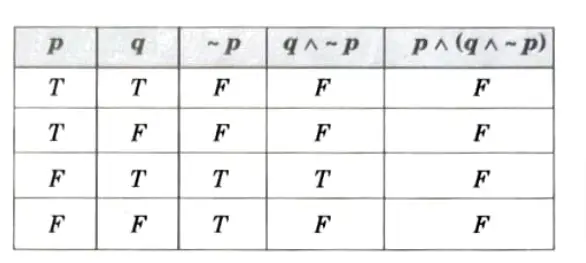
Q8. Verify that the proposition p ⋀ (q ⋀ -p) is a contradiction.
Ans.


Q9. Show that [(p V g) → r) ⋀ (-p)] → (q ⋀ r) is tautology or contradiction.
Ans.
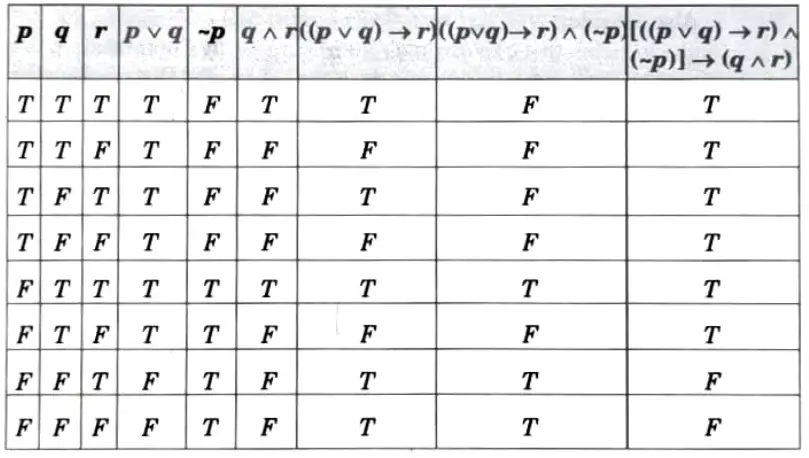


Question is incorrect. Since the result of the question is contingency.
Q10. What are the contrapositive, converse, and the inverse of the conditional statement: “The home team wins whenever it is raining”?
Ans.



Q11. Show that ㄱ(p ⋁ q) and ㄱ p ⋀ ㄱ q are logically equivalent.
Ans.



Q12. Find the contrapositive of “If he has courage, then he win”.Ans. If he will not win then he does not have courage.
Unit – 5 (Trees, Graph and Combinatorics)
Q1. Explain trivial tree and non-trivial tree.
Ans. A trivial tree is one that has just one vertex. A non-trivial tree is one that has more than one vertex.
Q2. Describe the terms rank and nullity.
Ans.



Q3. Define binary tree traversal with example.
Ans. A traversal of tree is a process in which each vertex is visited exactly once in a certain manner.
Binary tree traversal is of three types :
1. Preorder traversal
2. Postorder traversal
3. Inorder traversal
For example:
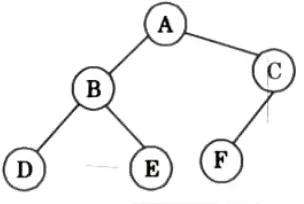


Preorder (NLR) : ABDECF
Postorder (LRN) : DEBFCA
Inorder (LNR) : DBEAFC
Q4. Define binary search trees.
Ans. A binary search tree is a binary tree T where the vertices are linked to data. Each data item in the left subtree of V is smaller than the data item in Vand, and each data item in the right subtree of V is more than the data item in Vand for each vertex V in T.
Q5. Give various representation of binary tree.
Ans. Various representation of binary tree are:
i. Storage representation
ii. Sequential representation
iii. Linked representation
Q6. Let G be a graph with ten vertices. If four vertices has degree four and six vertices has degree five, then find the number of edges of G.
Ans.
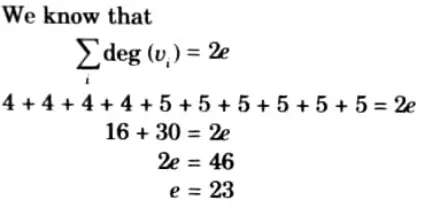
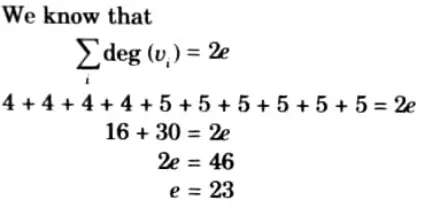
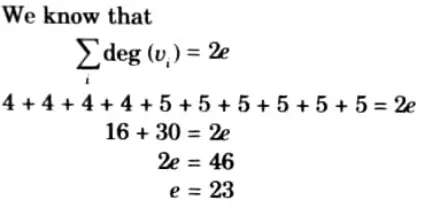
Q7. State the applications of binary search tree.
Ans. One of the most popular uses is to easily access and explore stored items by efficiently storing data in sorted form. For instance, the C++ Standard Library’s std:: map and std:: set. For many different implementations of expression parsers and expression solvers, binary trees as a data structure are helpful.
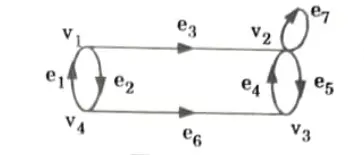
Q8. Define multigraph. Explain with example in brief.
Ans. A multigraphs G(V, E’) consists of a set of vertices V and a set of edges E such that edge set E may contain multiple edges and self loops.
Example :
a. Undirected multigraph:



B. Directed multigraph:


Q9. Find the recurrence relation from yn = A2n + B(-3)n.
Ans.



Q10. Find the minimum number of students in a class to show that five of them are born in same month.
Ans. Using pigeonhole principle:
Five of them are born in same month, so n = ?, m = 12.
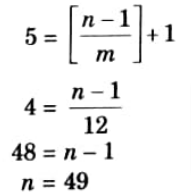
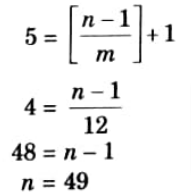
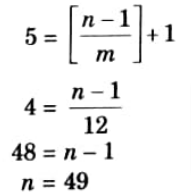
∴ 49 students are there to show that at least 5 of them are born in same month.
Q11. Explain edge coloring and k-egde coloring.
Ans. Edge coloring: The line graph L(G), which has a vertex for each edge of G and an edge for each pair of adjacent edges in G, can be thought of as having the same vertex colouring as a graph’s edge colouring.
k-edge coloring: A proper edge coloring with k different colors is called a (proper) k-edge coloring.
Q12. A tree has two vertices of degree 2, one vertex of degree 3 and three vertices of degree 4. How many vertices of degree 1 does it have? Ans. Let x be the required number. Now, total number of vertices
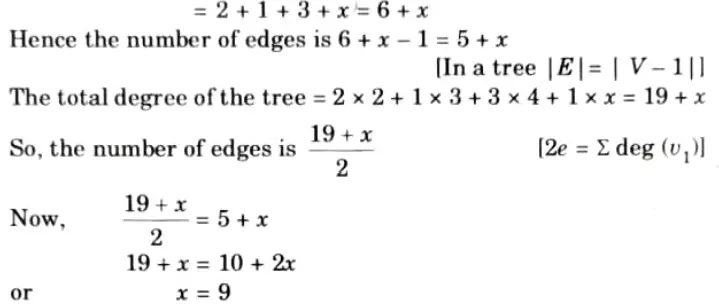
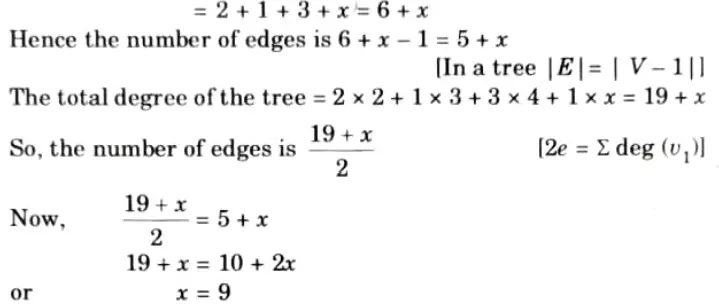
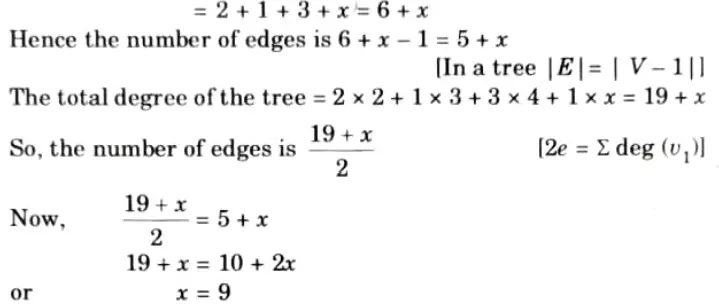
Thus, there are 9 vertices of degree one in the tree
Q13. State and prove pigeonhole principle.
Ans. Pigeonhole principle:Ifn pigeons are assigned tom pigeonholes then at least one pigeon hole contains two or more pigeons (m <n).
Proof:
1. Let m pigeonholes be numbered with the numbers 1 through m.
2. Beginning with the pigeon 1, each pigeon is assigned in order to the pigeonholes with the same number.
3. Since m < n i.e., the number of pigeonhole is less than the number of pigeons, n – m pigeons are left without having assigned a pigeon hole.
4. Thus, at least one pigeonhole will be assigned to a more than one pigeon.
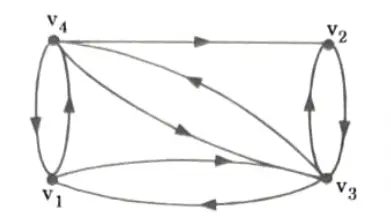
Q14. Draw the digraph G corresponding to adjacency matrix.



Ans. Since the given matrix is square matrix of order four, the graph G has 4 vertices v1, v2, v3 and v4. Draw an edge from vi to vj where aij = 1. The required di graph is shown in Fig.


Q15. A connected plane graph has 10 vertices each of degree 3. Into how many regions, does a representation of this planar graph split the plane ?
Ans.
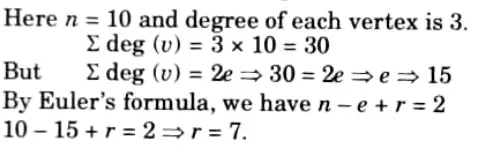
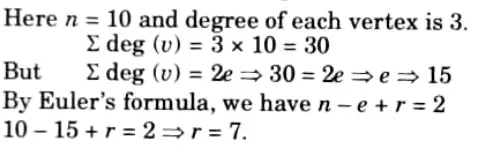
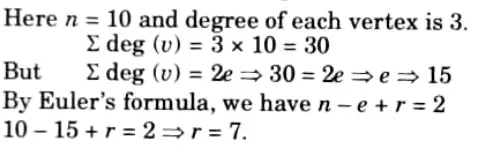
Q15. How many permutations of the letters of the word BANANA?
Ans. There are 6 letters in the word BANANA of which three are alike of one kind (3A’s), two are alike of second kind (2N’s) and the rest one letter is different.
Hence, the required number of permutations =6!/3!2! = 60
Q16. How many 4 digit numbers can be formed by using the digits 2, 4, 6,8 when repetition of digits is allowed?
Ans. When repetition is allowed:
The thousands place can be filled by 4 ways.
The hundreds place can be filled by 4 ways.
The tens place can be filled by 4 ways.
The units place can be filled by 4 ways.
∴ Total number of 4 digit number = 4 x 4 x 4 x 4=256
Q18. How many bit strings of length eight either start with a’1′ bit or end with the two bit ’00’?
Ans. 1. Number of bit strings of length eight that start with a 1 bit : 27 = 128.
2. Number of bit strings of length eight that end with bits 00 : 26 = 64.
3. Number of bit strings of length eight 25 = 32 that start with a 1 bit and end with bits 00: 25= 32
Hence, the number is 128 + 64 32 160.
Q19. Define Eulerian path, circuit and graph.
Ans. Eulerian path: A path of graph G which includes each edge of G exactly once is called Eulerian path.
Eulerian circuit: Acircuit of graph G which include each edge of G exactly once.
Eulerain graph: A graph containing an Eulerian circuit is called Eulerian graph.
Q20. Define chromatic number and isomorphic graph.
Ans. Chromatic number: The chromatic number of a graph is the bare minimum of colours needed to properly colour a graph so that no two neighbouring vertices have the same colour.
Isomorphic graph: If two graphs are isomorphic to each other then:
i. Both have same number of vertices and edges.
ii Degree sequence of both graphs are same (degree sequence is the sequence of degrees of the vertices of a graph arranged in nonincreasing order).
Q21. Define walk.
Ans. In a graph G, a finite alternating sequence of vertices and edges v1, e1, v2,, e2…..starting and ending with vertices such that each edge in sequence is incident with the vertices following and preceding, it is called walk.
Q22. Define non-planar graph. Ans. If a graph G cannot be drawn in a plane without any edges crossing, it is said to be non-planar.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Discrete Structures and Theory of Logics Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Discrete Structures and Theory of Logics Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
