Prepare to dig into Discrete Structure Unit 5 at AKTU! For Btech students, this course is all about tree structures, graph theory, counting ideas, and their interesting practical applications in the field of computer science and network analysis. Let’s go exploring!
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Discrete Structures and Theory of Logics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Section A : Short Questions in Discrete Structure And Theory of Logic
a. Let A = {1, 2, 3, 4, 5, 6} be the set and R = {(1, 1) (1, 5) (2, 2) (2, 3) (2, 6) (3, 2) (3, 3) (3, 6) (4, 4) (5, 1) (5, 5) (6, 2) (6, 3) (6, 6)} be the relation defined on set A.
Find equivalent classes induced by R.
Ans. Given: A = {1, 2, 3, 4, 5, 6} and
R = {(1, 1) (1, 5) (2, 2) (2, 3) (2, 6) (3, 2) (3, 3) (3, 6) (4, 4) (5, 1) (5, 5) (6, 2) (6, 3) (6, 6)}
Now, finding equivalence class as
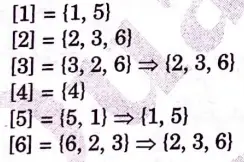
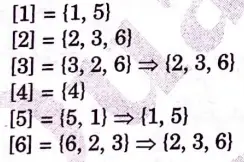
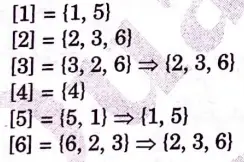
b. Solve Ackermann function A (2, 1).
Ans. Given: A(2, 1)
Here m = 2 and n = 1
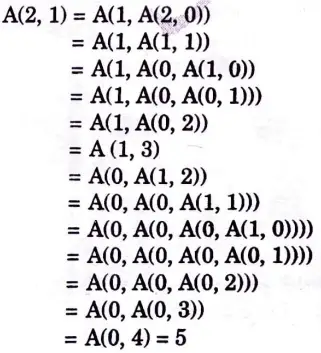
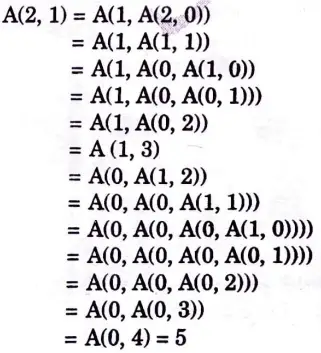
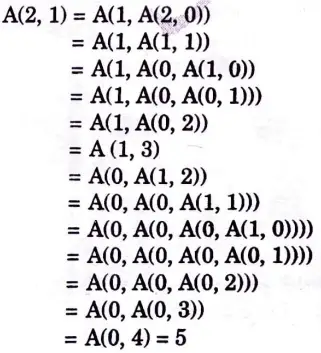
c. State and justify “Every cyclic group is an abelian group”.
Ans. Let G be a cyclic group and let a be a generator of G so that
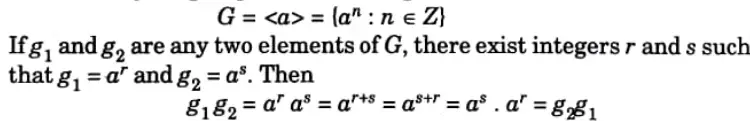
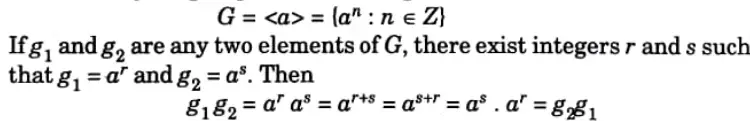
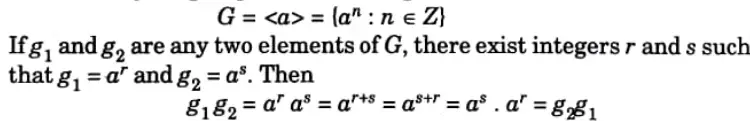
So, G is abelian.
d. State Ring and Field with examples.
Ans. Ring: A ring is an algebraic system (R, +, ⦁) where R is a non-empty set and + and ⦁ are two binary operations (which can be different from addition and multiplication) and if the following conditions are satisfied:
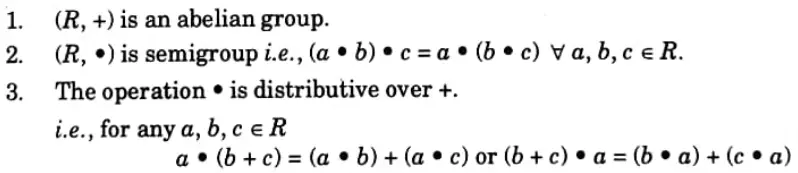
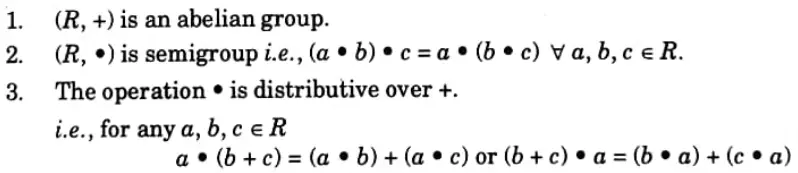
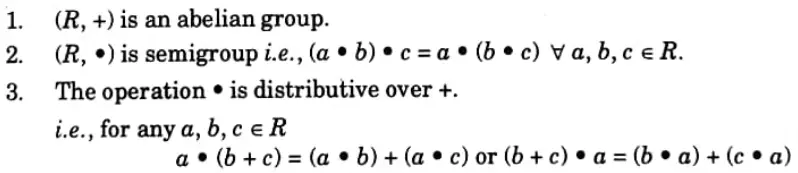
e. Differentiate complemented lattice and disturbed lattice.
Ans. Complemented lattice : Let L be a bounded lattice with greatest element 1 and least element 0. Let a ∈ L then an element a’ ∈ L is complement of a if,
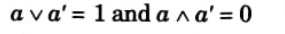
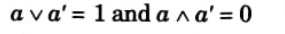
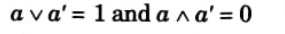
A lattice L is called complemented if is bounded and if every element in L has a complement.
Distributive lattice: A lattice L is said to be distributive if for any element a, b and c of L following properties are satisfied :
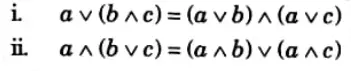
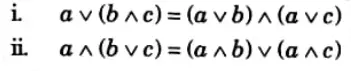
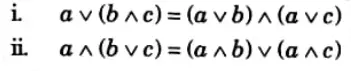
otherwise L is non-distributive lattice.
f. State De Morgan’s law and Absorption law.
Ans. a. Absorption law:
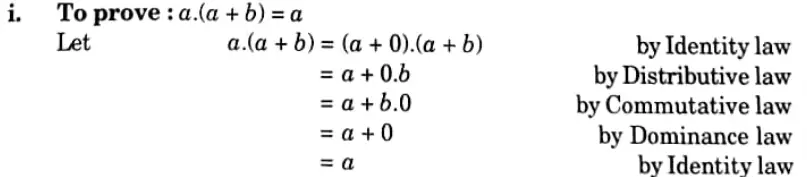
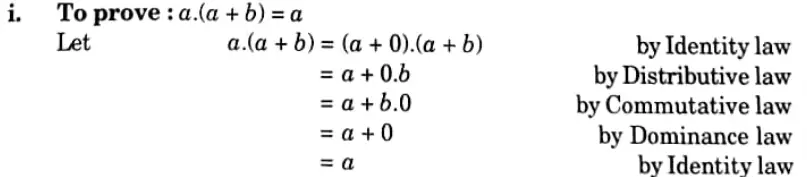
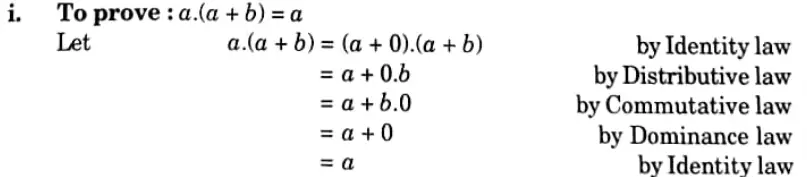
b. De Morgan’s law:
i. To prove: (a + b)’ = a’.b’
To prove the theorem we will show that



g. Translate the conditional statement “If it rains, then I will stay at home” into contrapositive, converse and inverse statement.
Ans. Let, p : It rains
q : I will stay at home
Symbolic form is given statement is
p → q
Converse : q → p
i.e., If I will stay at home, then it rains.
Inverse : -p → -q
i.e., If it does not rain, then I will not stay at home.
Contrapositive : ~p → ~q
i.e., If I will not stay at home, then it does not rain.
h. State Universal Modus Ponens and Universal Modus Tollens laws.
Ans. Universal modus ponens: By this rule if P(x) → Q(x) is true for every x and P(c) is true for some particular member c in UD then Q(c) is true.
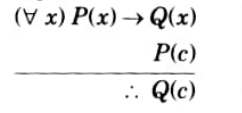
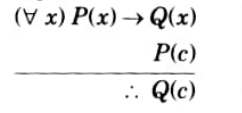
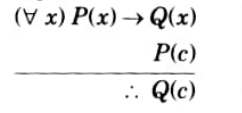
Universal modus tollens: By this rule if P(x) → Q(x) is true for every x and Q(c) is true for some particular c in UD then -Q(c) is true.
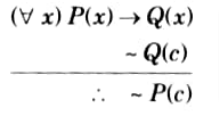
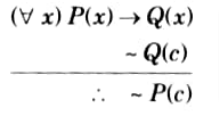
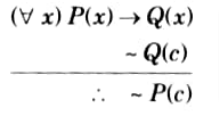
i. Explain Euler’s formula. Determine number of regions if a planar graph has 30 vertices of degree 3 each.
Ans. Euler’ formula:
F + V = E + 2
where, F = Number of faces
V = Number of vertices
∈ = Number of edges
Numerical:
Given: V = 30, ∈ = 3
To Find: F = ?
F = | ∈ + 2 -V |
= | 5 – 30 | = 25
j. Explain pigeonhole principle with example.
Ans. In counting methods, the pigeonhole principle can occasionally be helpful. If n pigeons are assigned to m pigeonholes then at least one pigeonhole contains two or more pigeons (m < n).
Proof:
- 1. Let m pigeonholes be numbered with the numbers 1 through m.
- 2. Each pigeon is assigned in sequence to the pigeonholes with the same number, starting with pigeon 1.
- 3. Since m < n i.e., the number of pigeonhole is less than the number of pigeons, n-m pigeons are left without having assigned a pigeonhole.
- 4. Thus, at least one pigeonhole will be assigned to a more than one pigeon.
- 5. We see that the pigeonhole principle does not provide any guidance on where to look for the pigeonhole that has two or more pigeons.
- 6. It only asserts the existence of a pigeon hole containing two or more pigeons.
- 7. To put the theory into practise, one must choose which objects will serve as pigeons and which objects will serve as pigeonholes.
Section B: Long Question in Discrete Structure And Theory of Logic
a. Justify that for any set A, B and C:
i. (A – (A ◠ B)) = A – B
ii. (A – (B ◠C)) = (A – B) ◡ (A – C)
Ans.



b. Explain cyclic group. Let H be a subgroup of a finite group G. Justify the statement “the order of H is a divisor of the order of G”.
Ans. Cyclic group: A group Gis called a cyclic group if Ǝ at least one element a in G such that every element x ∈ G is of the form an, where n is some integer. The element a ∈ G is called the generator of G.
For example:
Show that the multiplicative group G = (1,-1,i,-i) is eyelíc. Also find its generators.
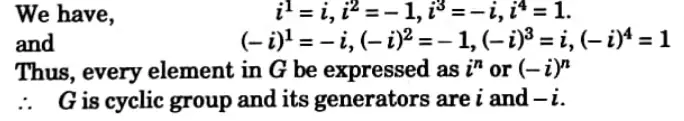
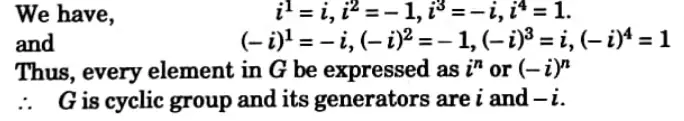
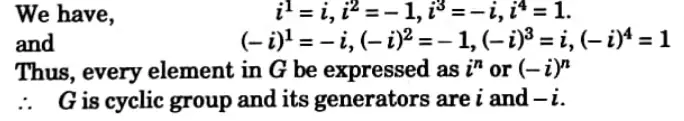
Let G be a group of finite order n. Let H be a subgroup of G and let
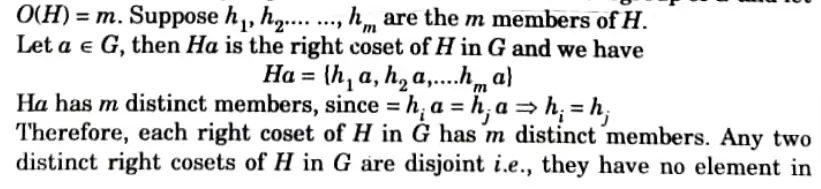
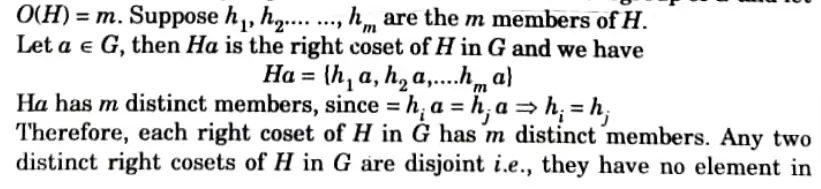
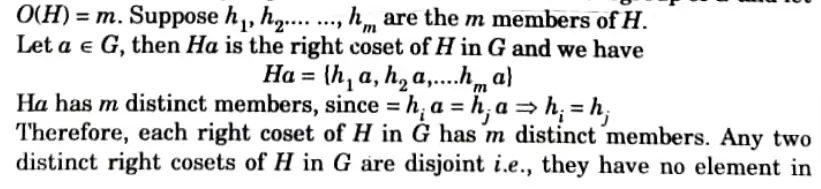



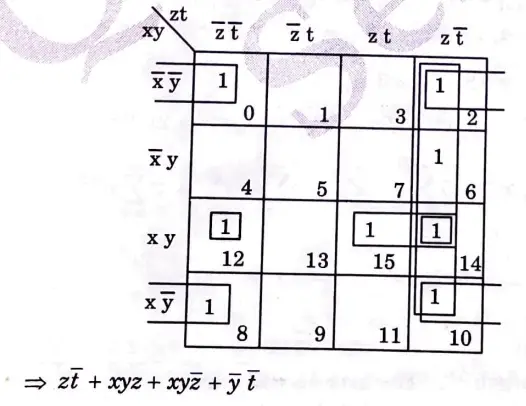
c. Solve E(x,y,z,t) = Σ(0,2,6,8,10,12,14,15) using K-map.
Ans.


d. Construct the truth table for the following statements:
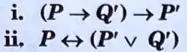
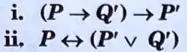
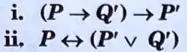
Ans.
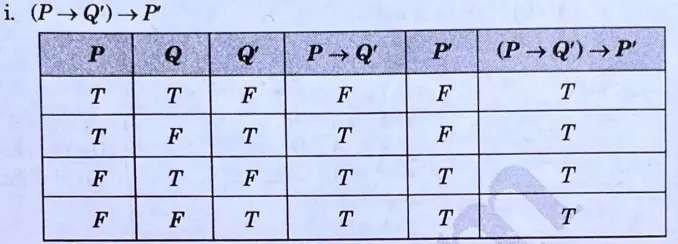


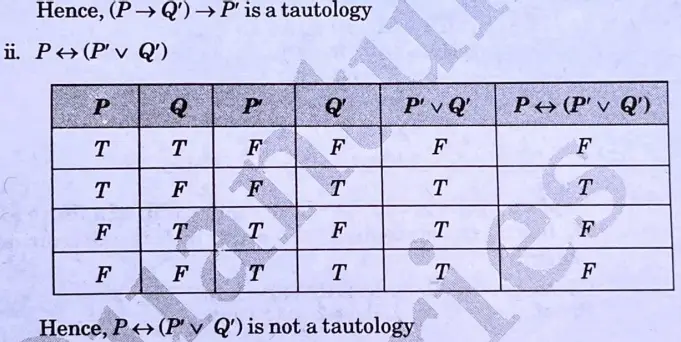


e. Solve the recurrence relation using generating function:
an+2 – 5an+1 + 6an = 2, with a0 = 3 and a1 = 7.
Ans. Given: an+2 – 5an+1 + 6an = 2
with a0 = 3, a1 = 7
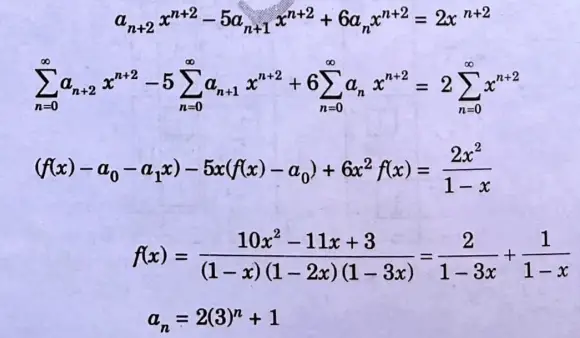
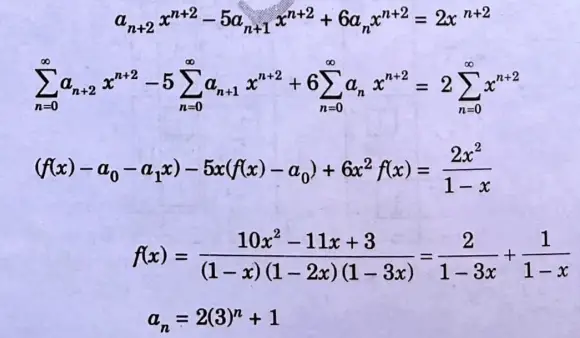
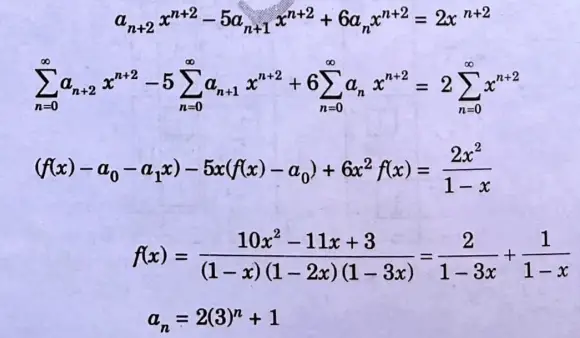
Section C: Long Important Question
a. State principle of duality. Let A denote the set of real numbers and a relation R is defined on A such that (a, b)R (c, d) if and only if a2 + b2 = c2 + d2. Justify that R is an equivalence relation.
Ans. Principle of duality: According to the principle of duality, two concepts can only be interchanged if all the findings that hold true for one formulation also hold true for the other. This is a type of ubiquitous property of algebraic structure. Dual formulation is the name given to this idea.
Numerical: a2 + b2 = c2 + d2
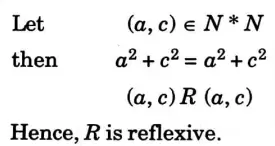
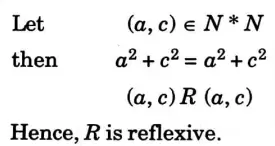
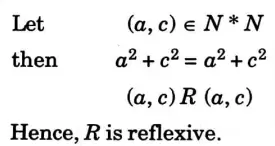
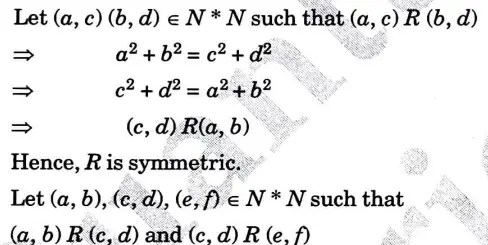
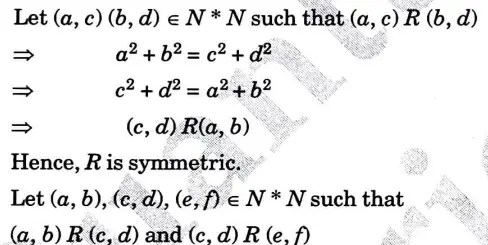
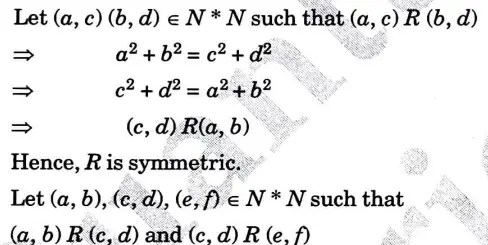
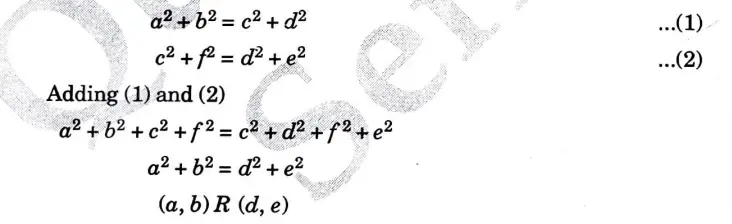
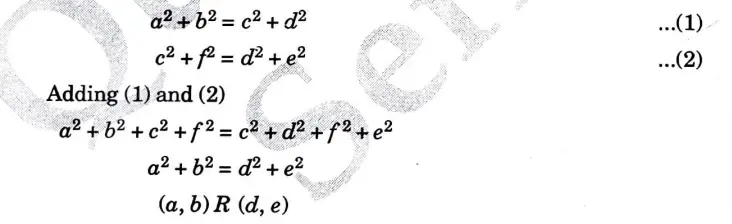
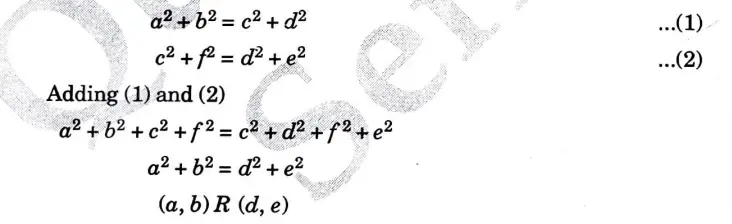
Hence, R is transitive.
Hence, R is an equivalence relation.
b. i. Let R = (1, 2) (2, 3) (3, 1) defined on A = {1, 2, 3}. Find the transitive closure of R using Warshall’s algorithm.
ii. Justify that “If f : A → B and g : B → C be one-to-one onto function, then gof is also one to one onto and (gof)-1 = f-1o g-1”.
Ans. i. R = (1, 2) (2, 3) (3, 1)
Step 1: Representing the relation R in Matrix form
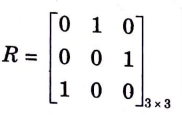


Step 2: Now, consider Column 1 and Row 1 of the above matrix
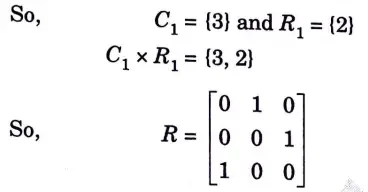
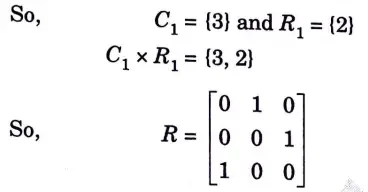
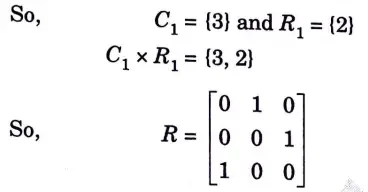
Step 3: Now consider Column 2 and Row 2 of above matrix
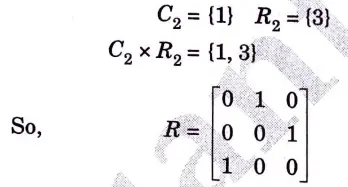
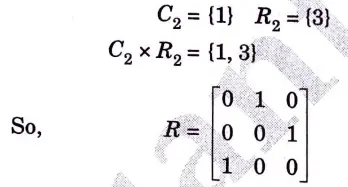
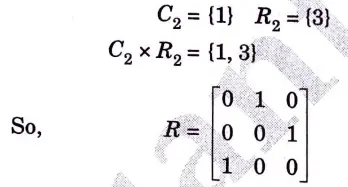
Step 4: Now consider C3 and R3
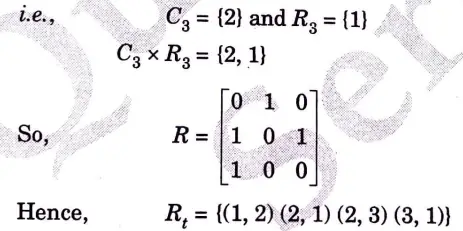
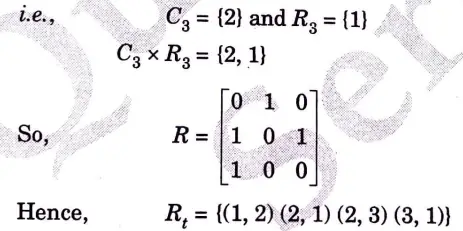
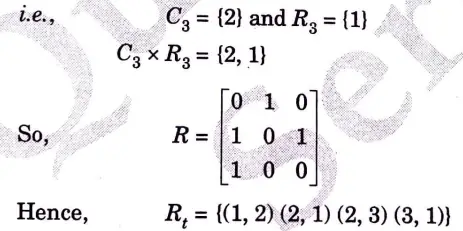
ii.
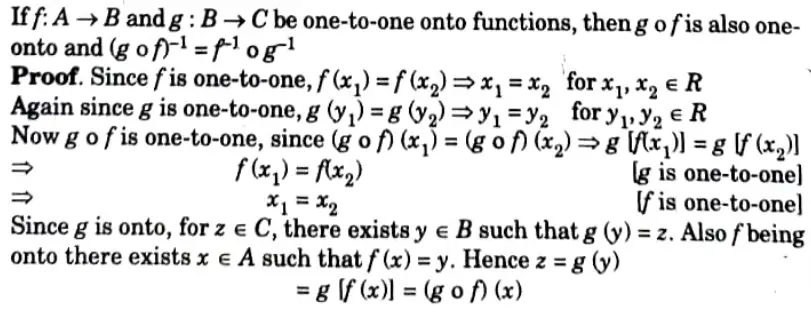
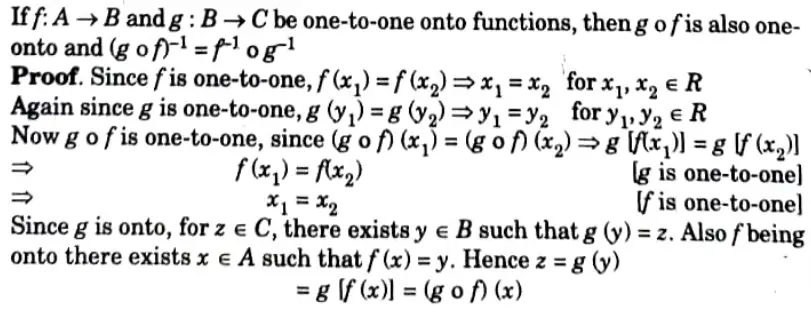
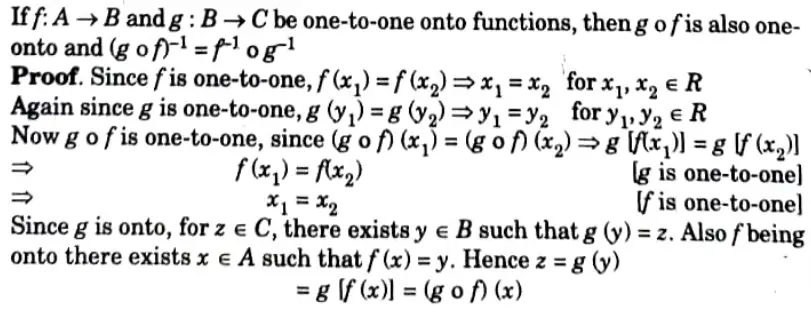



Section 4: Important Long Question
a. Define the binary operation * on Z by x * y = x + y +1 for all x, y belongs to set of integers. Verify that (Z, *) is abelian group? Discuss the properties of abelian group.
Ans.
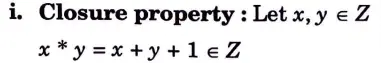
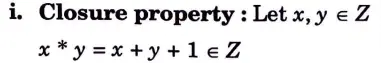
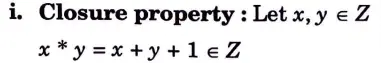



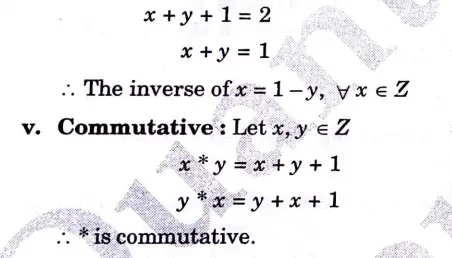
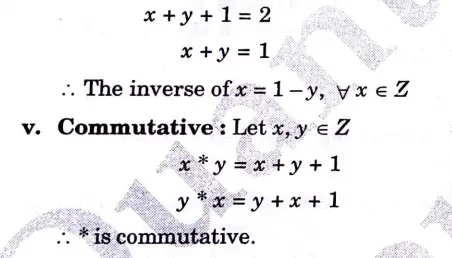
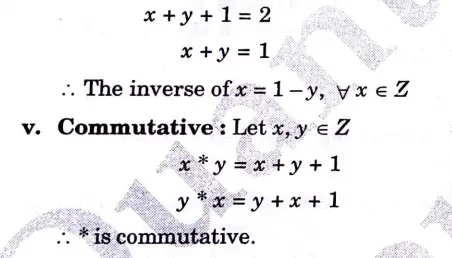
Thus, (Z, *) is an abelian group.
Properties of abelian group: An abelian group G is a group for which the element pair (a, b) ∈ G always holds commutative law. An abelian group satisfy five properties: Closure Property, Associate Property, Identify Property, Inverse Property, and Commutative Property.
b. i. Justify that “The intersection of any two subgroup of a group (G, *) is again a subgroup of (G, *)”.
ii. Justify that “If a, b are the arbitrary elements of a group G then (ab)2 = a2b2 if and only if G is abelian.
Ans. i.
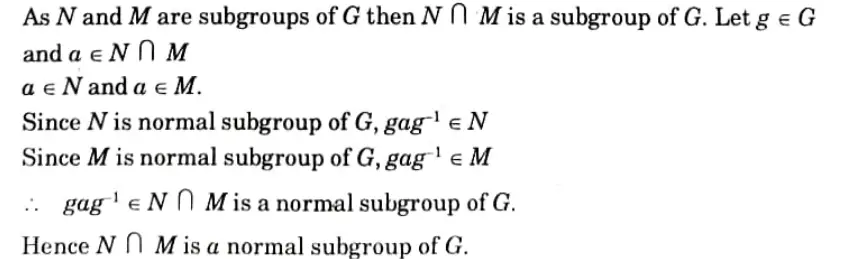
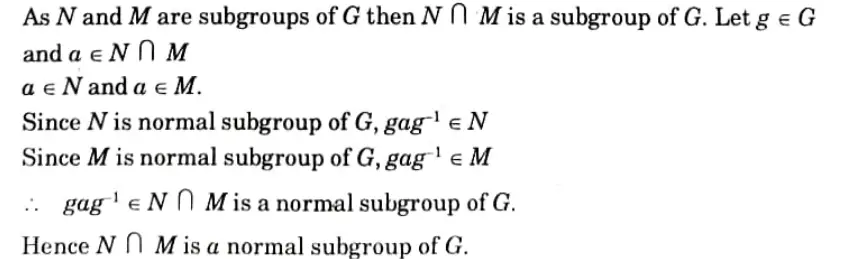
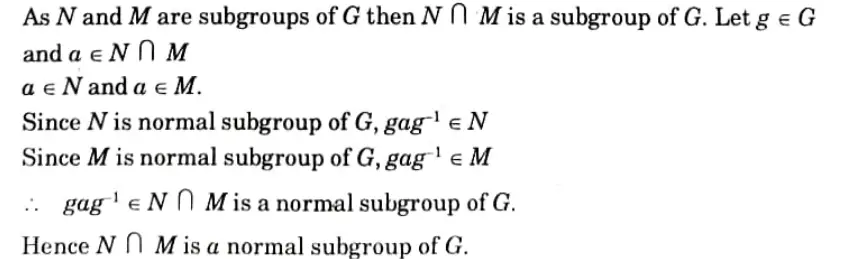
ii. Let G is an abelian group
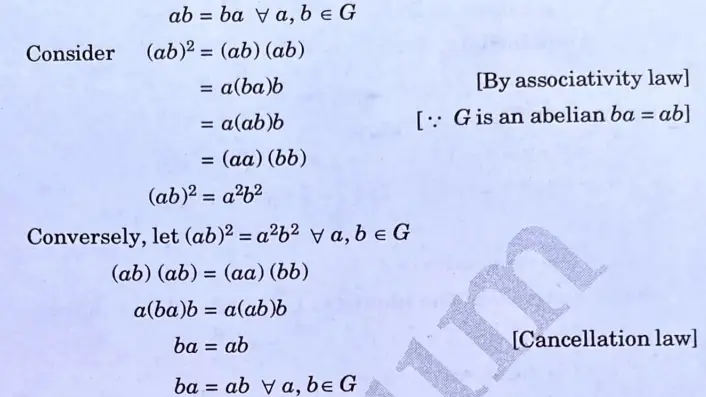
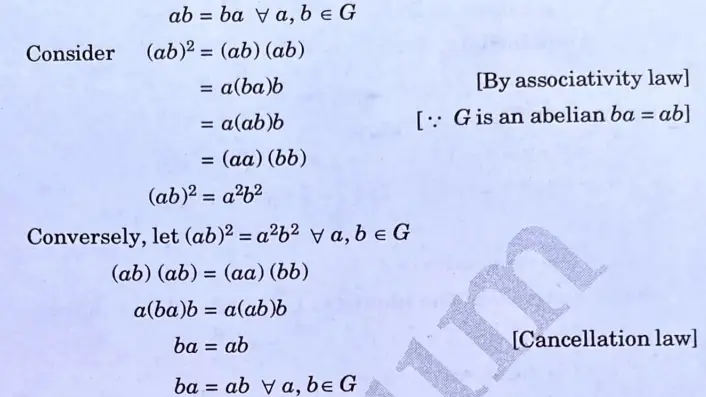
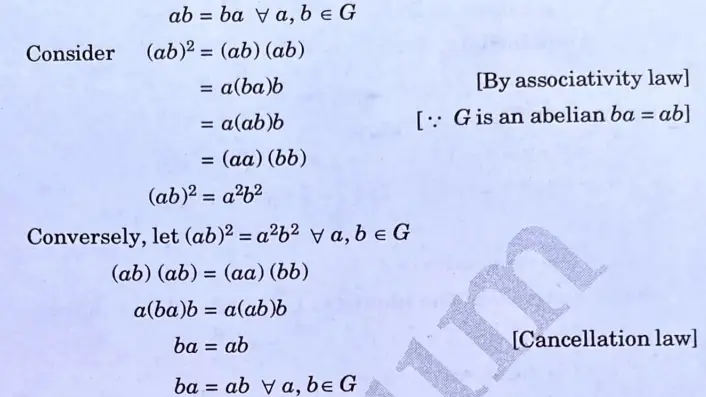
Section 5: Important Long Question in Discrete Structure
a. Define modular lattice. Justify that if ‘a’ and ‘b’ are the elements in a bounded distributive lattice and if ‘a’ has complement a’, then
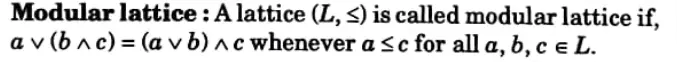
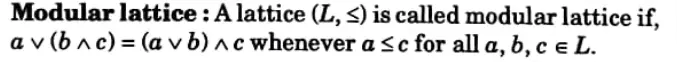
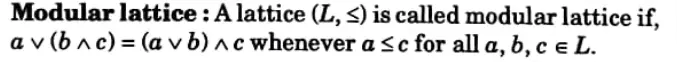
Ans.
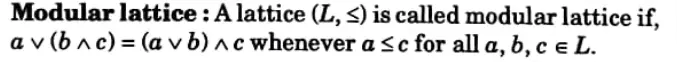
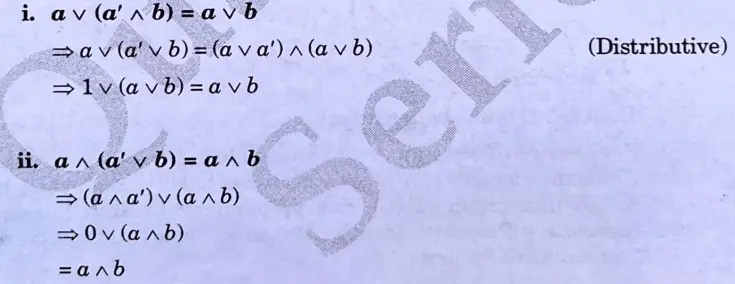
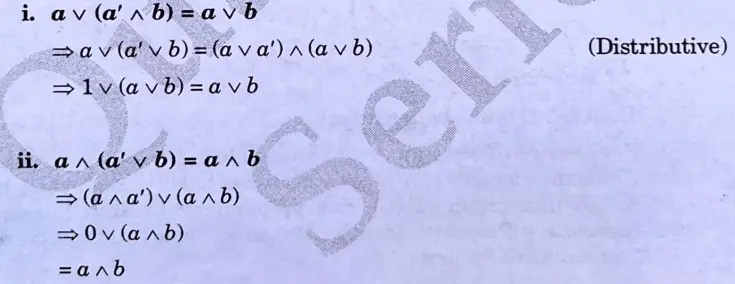
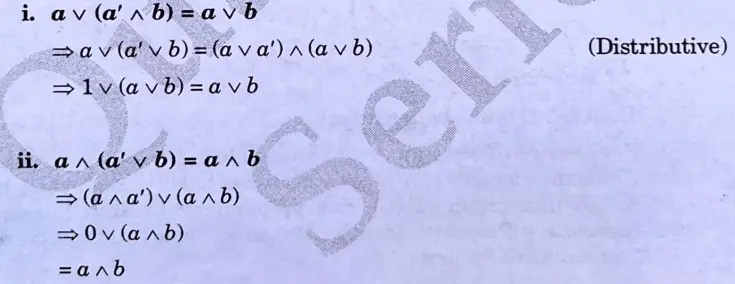
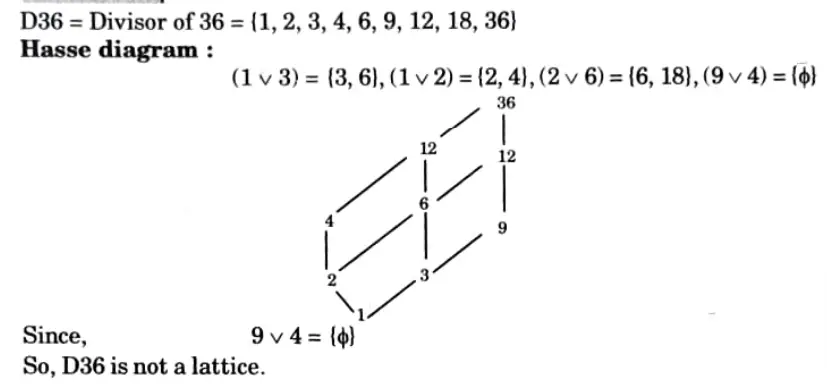
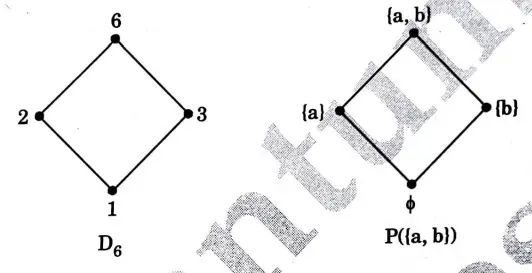
b. i. Justify that (D36, \) is lattice.
ii. Let L1 be the lattice defined as D6 and L2 be the lattice (p(S), ⊆), where P(S) be the power set defined on set defined on set S = {a, b}. Justify that the two lattices are isomorphic.
Ans. i.


ii. Let A = {a, b} and P(S) = {ɸ, {a}, {b}, {a, b}. Then the lattice (P(S),⊆) is isomorphic to lattice (D6, 1)with divisibility as the partial order relation . In fact, we define a mapping f: D6 → P(S) by
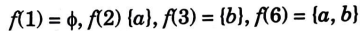
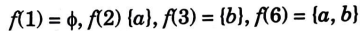
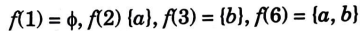
Then, f is bijective and we note that
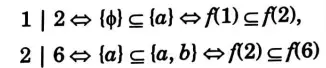
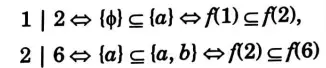
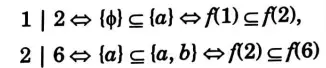
and so on. Hence f is isomorphism. Thus, the two lattices are isomorphic.


a. Use rules of inference to justify that the three hypotheses
i. “If it does not rain or if it is not foggy, then the sailing race will be held and the lifesaving demonstration will go on.”
ii. “If the sailing race is held, then the trophy will be awarded.”
iii. “The trophy was not awarded .” imply the conclusion
iv. “It rained.”
Ans. Let r be the proposition “It rains,” let f be the proposition “It is foggy,” let s be the proposition “The sailing race will held,” let l be the proposition “The life saving demonstration will go on,” and let t be the proposition “The trophy will be awarded .” We are given premises






b. Justify that the following premises are inconsistent:
i. If Nirmala misses many classes through illness then she fails high school.
ii. If Nirmala fails high school, then she is uneducated.
iii. If Nirmala reads a lot of books then she is not uneducated.
iv. Nirmala misses many classes through illness and reads a lot of books.
Ans. Let,
C = Nirmala misses many classes through illness
F = Nirmala fails high school
Ε = Nirmala is uneducated
B = Nirmala reads lot of books
Symbolic representation is



The set of given premises are inconsistent.
Section 7 : Important Long Question
a. Explain the following terms with example:
i. Graph coloring and chromatic number.
ii. How many edges in K7 and K33.
iii. Isomorphic graph and hamitonian graph.
iv. Bipartite graph.
v. Handshaking theorem.
Ans. i. Chromatic number: The chromatic number of a graph is the bare minimum of colours needed to properly colour a graph so that no two neighbouring vertices have the same colour.
ii.
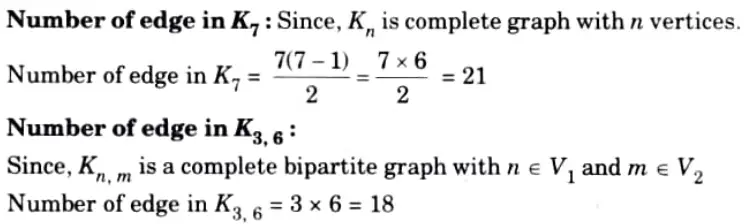
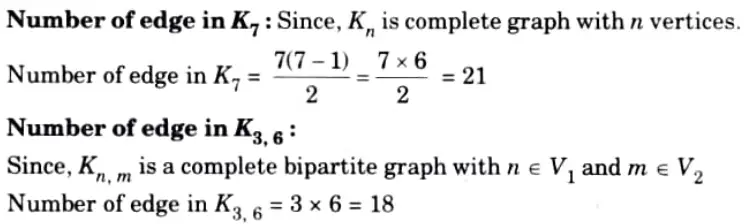
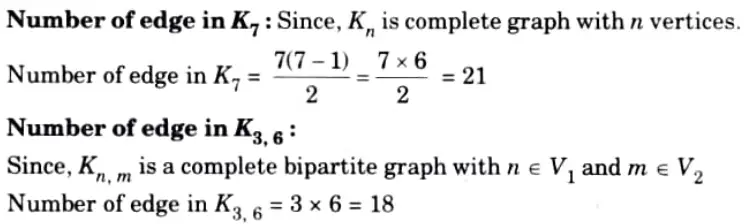
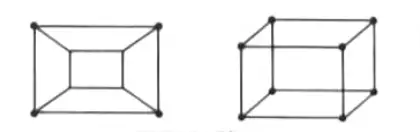
iii. Isomorphic graph: Two graphs are isomorphic to each other if:
i. Both have same number of vertices and edges.
ii. Both graphs’ degree sequences are the same (degree sequence is the sequence of degrees of the vertices of a graph arranged in non-increasing order).
Example:


Hamiltonian graph: A closed path called a Hamiltonian circuit traverses every vertex in a graph G exactly once, with the exception of the end vertices. If a Hamiltonian circuit exists, a graph G is referred to as a Hamiltonian graph.
For example: Consider graphs given below:
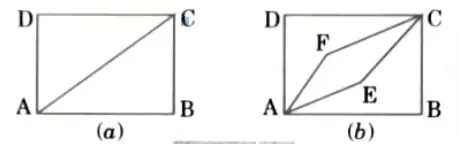


Graph given is Fig. (a) is a Hamiltonian graph since it contains a Hamiltonian circuit A -B-C-D-A while graph in Fig (b) is not a Hamiltonian graph.
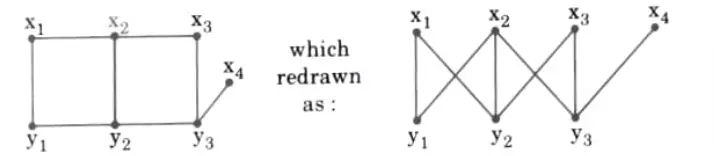
iv. Bipartite graph: A graph G = (V, E) is bipartite if the vertex set V can be partitioned into two subsets (disjoint) V1 and V2 such that every edge in E connects a vertex in V1 and a vertex V2 (so that no edge in G connects either two vertices in V1 or two vertices in V2. (V1,V2) is called a bipartition of G.


v. Handshaking theorem:
- 1. Handshaking theorem states that the sum of degrees of the vertices of a graph is twice the number of edges.
- 2. If G = (V, E) be a graph with E edges, then Σ degG(V) = 2E.
- 3. The following conclusion may be drawn from the handshaking Theorem:
- In any graph,
- i. The sum of degree of all the vertices is always even.
- ii. The sum of degree of all the vertices with odd degree is always even.
- iii. The number of vertices with odd degree are always even.
b. i. Justify that “In a undirected graph the total number of odd degree vertices is even”.
ii. Justify that “The maximum number of edges in a simple graph is n(n-1)/2”.
Ans. i. Let G = (V, E) a undirected graph,
Let U denote the set of even degree vertices in G and W denote the set of odd degree vertices.
Then,
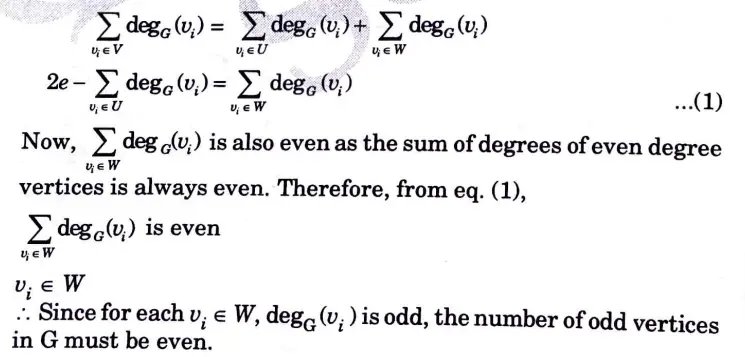
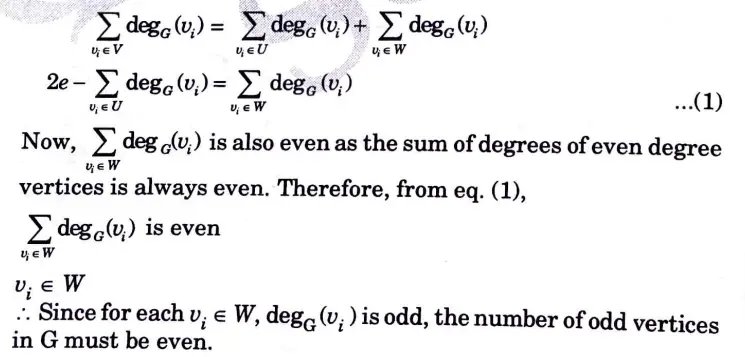
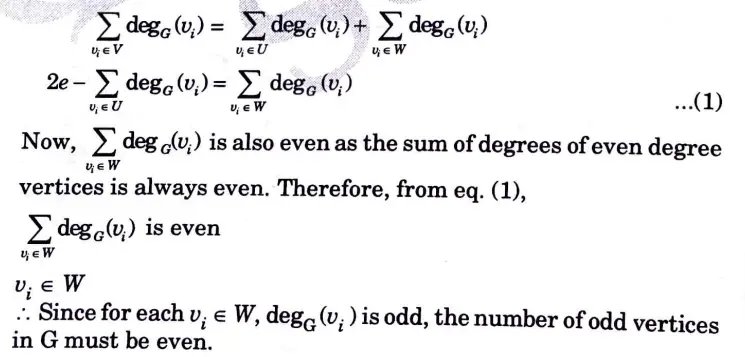
ii.
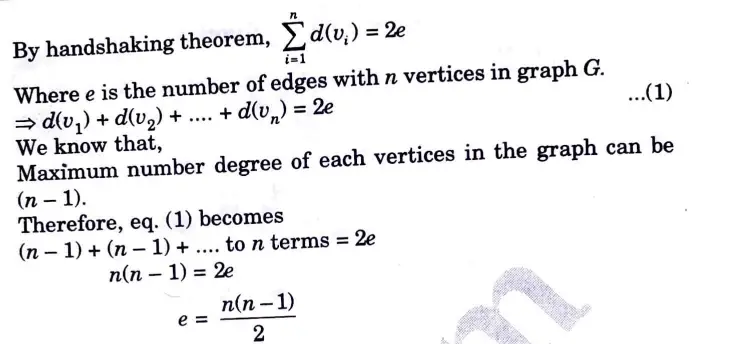
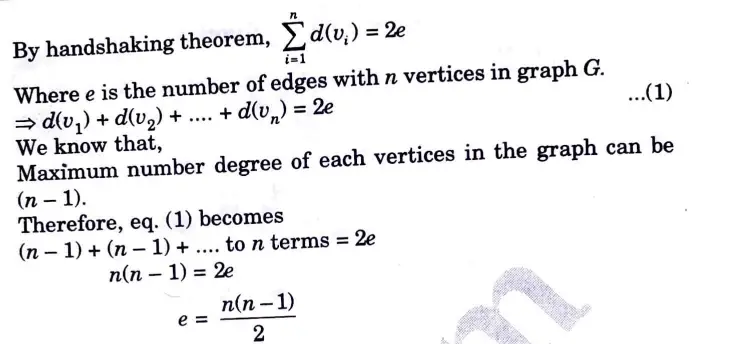
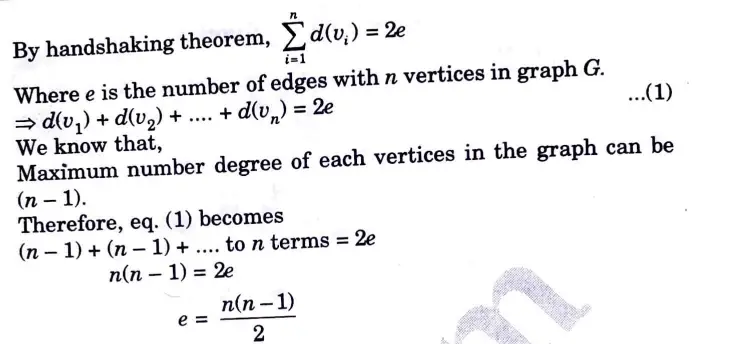



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Discrete Structures and Theory of Logics Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Discrete Structures and Theory of Logics Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
