Boost your CBSE 10th Class MATHEMATICS skills with our detailed notes, solved problems, and critical questions. Improve your maths skills by using these helpful tools.
Time allowed:3 Hours Maximum Marks:80
SECTION – A
1. If HCF (336, 54) = 6, find LCM (336, 54). [1]
Sol. Given, HCF (336, 54) = 6
We know,
HCF x LCM = one number x other number
⇒ 6 x LCM = 336 x 54
⇒ LCM = 336 x 54 / 6
= 336 x 9
= 3024 Ans.
2. Find the nature of roots of the quadratic equation [1]
2x2 – 4x + 3 = 0.
Sol. Given, 2x2 – 4x + 3 = 0
Comparing it with quadratic equation
ax2 + bx + c = 0
Here, a = 2, b = -4 and c = 3
∴ D = b2 – 4ac
= (-4)2 – 4 x (2) (3)
= 16 – 24
= -8 < 0
D < 0 shows that roots will not be real. Hence, roots will be imaginary. Ans.
3. Find the common difference of the Arithmetic Progression (A.P) [1]

Ans. Given,
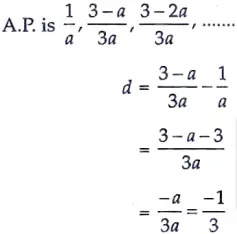
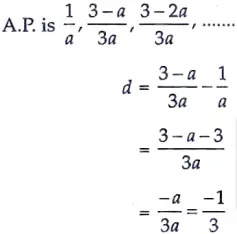
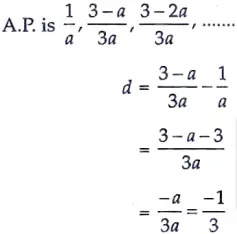
4. Evaluate : sin2 60° + 2 tan 45°- cos2 30° [1]
Sol. We know,
sin 60° = √3/2, tan 45° = 1 and cos 30° = √3/2
∴ sin2 60° +2 tan 45° – cos2 30°
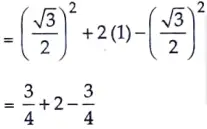
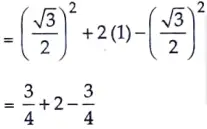
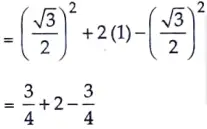
= 2 Ans.
OR
If sin A = 3/4, calculate sec A.
Sol. Given, sin A = 3/4
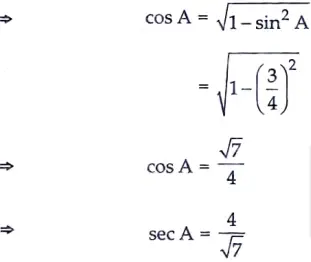
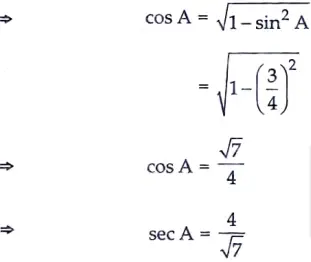
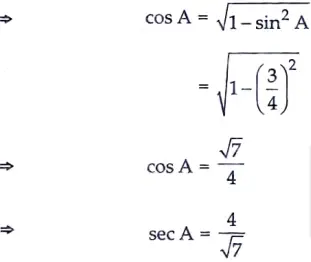
5. Write the coordinates of a point P on x-axis which is equidistant from the point A(-2, 0) and B(6, 0). [1]
Sol. Let coordinates of P on x-axis is (x, 0)
Given, A(-2, 0) and B(6, 0)
Here, PA = PB
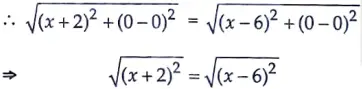
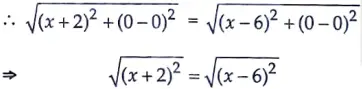
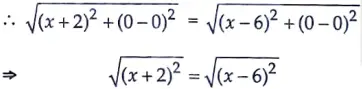
On squaring both sides, we get
(x + 2)2 = (x – 6)2
x2 + 4 + 4x = x2 + 36 – 12x
⇒ 4 + 4x = 36 – 12
⇒ 16x = 32
⇒ x = 32/16 = 2
Co-ordinates of P are (2, 0) Ans.
6. Find the 21″ term of the [1]
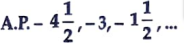
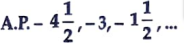
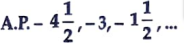
Sol. Given,
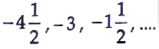
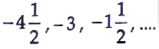
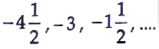
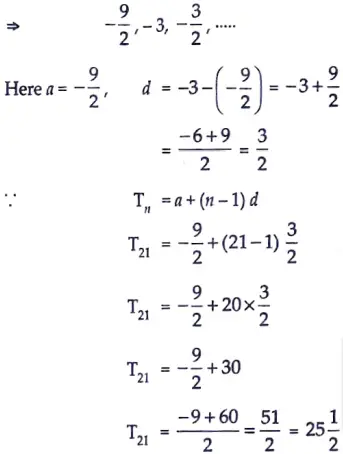
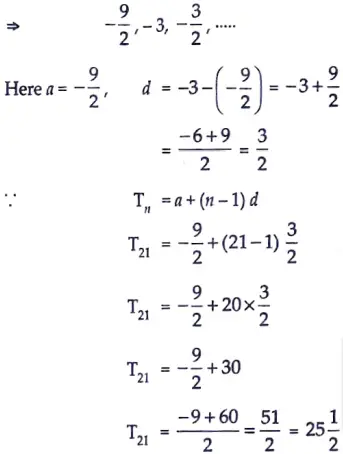
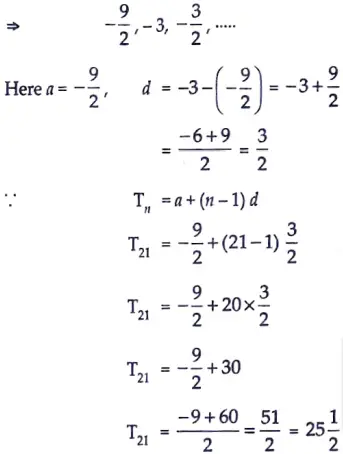
SECTION – B
7. A die is thrown twice. Find the probability that [2]
(i) 5 will come up at least once.
(ii) 5 will not come up either time.
Sol. When two dice are thrown simultaneously, all possible out comnes are
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
Total number of outcomes = 36
Total outcomes where 5 comes up at least once = 11
(i) Probability that 5 will come up at least once
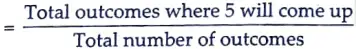
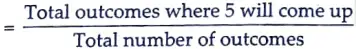
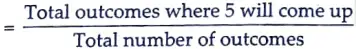
= 11/36
Total outcomes where 5 will not come up
= 36 – 11 = 25
(ii) Probability that 5 will not come up either time



= 25/36 Ans.
8. Find a relation between x and y if the points A(x, y), B(-4,6) and C(-2,3) are collinear.** [2]
OR
Find the area of a triangle whose vertices are given as (1, – 1) (-4,6) and (-3,- 5).**
9. The probability of selecting a blue marble at random from a jar that contains only blue, black and green marbles is 1/5 The probability of selecting a black marble at random from the same jar is 1/4. If the jar contains 11 green marbles, find the total number of marbles in the jar. [2]
Sol. Let probability of selecting a blue marble, black marble and green marble are P(x), P(y), P(z) respectively.
P(x) = 1/5, P(y) = 1/4
We know,
P(x) + P(y) + P(z) = 1
1/5 + 1/4 + P(z) = 1
9/20 + P(z) = 1
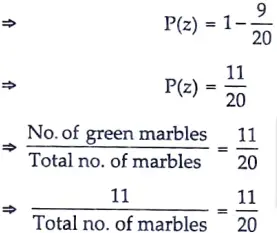
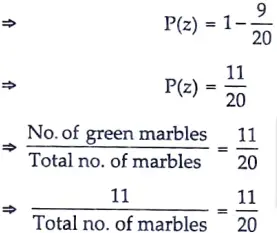
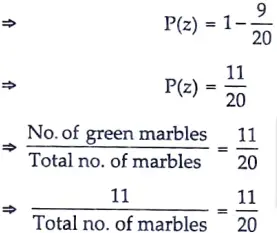
(∵ No. of green marbles = 11)
⇒ Total no. of marbles = 20
∴ There are 20 marbles in the jar. Ans.
10. Find the value(s) of k so that the pair of equations x + 2y = 5 and 3x + ky + 15 = 0 has a unique solution. [2]
Sol. Given, x + 2y = 5
3x + ky + 15 = 0
Comparing above equations with
a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0,
We get,
a1 = 1, b1 = 2, c1 = -5
a2 = 3, b2 = k, c2 = 15
Condition for the pair of equations to have unique solution is
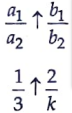


k ≠ 6
k can have any value except 6. Ans.
11. The larger of two supplementary angles exceeds the smaller by 18°, Find the angles. [2]
Sol. Let two angles A and B are supplementary.
∴ A + B = 180° …(i)
Given, A = B +18°
On putting A = B+ 18° in equation (i), we get
B + 18° + B = 180°
2B + 18° = 180°
⇒ 2B = 162°
⇒ B = 81°
⇒ A = B + 18°
⇒ A = 99° Ans.
OR
Sumit is 3 times as old as his son. Five years later, he shall be two and a half times as old as his son. How old is Sumit at present?
Sol. Let age of Sumit be x years and age of his son be y years. Then, according to question we have,
x = 3y .…(1)
Five years later,
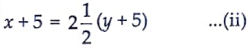
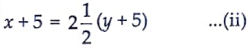
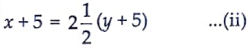
On putting x = 3y in equation (ii)
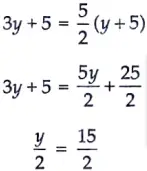
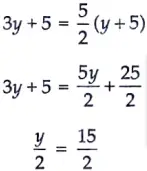
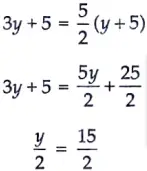
y = 15 years
Then, present age of sumit is
3 x y = 3 x 15
= 45 years Ans.
12. Find the mode of the following frequency distribution:
| Class Interval: | 25-30 | 30-35 | 35-40 | 40-45 | 45-50 | 50-55 |
| Frequency: | 25 | 34 | 50 | 42 | 38 | 14 |
Sol.
| Class Interval | Frequency |
| 25-30 | 25 |
| 30-35 | 34 |
| 35-40 | 50 |
| 40-45 | 42 |
| 45-50 | 38 |
| 50-55 | 14 |
Here, maximum frequency is 50.
So, 35-40 will be the modal class.
l = 35, f0 = 34, f1 = 50, f2 = 42 and h = 5
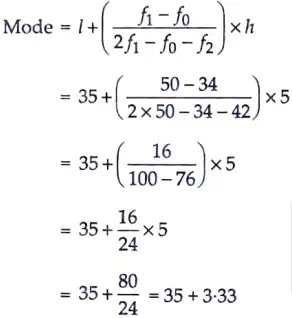
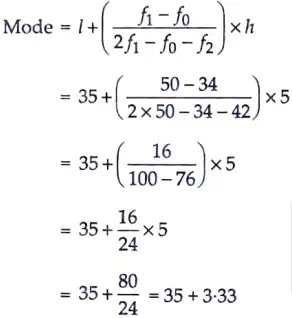
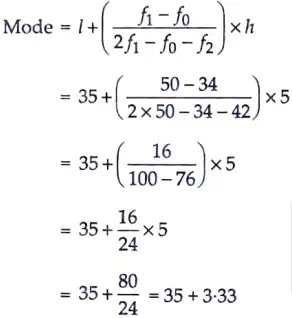
= 38.33 Ans.
SECTION – C
13. Find the ratio in which the y-axis divides the line segment joining the points (-1, -4) and (5, -6). Also find the coordinates of the point of intersection. [3]
Sol. Let the y-axis cut the line joining point A(- 1, -4) and point B(5, – 6) in the ratio k : 1 at the point P(0, y)
Then, by section formula, we have



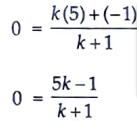
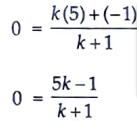
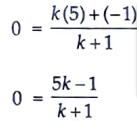
⇒ 5k – 1 = 0
k = 1/5
Then the required ratio is (1/5:1) i.e., (1 : 5)
Again, by section formula, we have
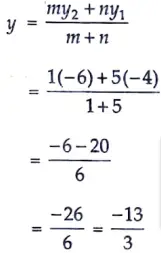
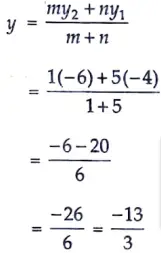
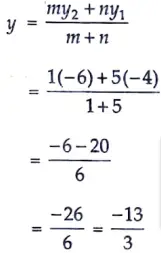
Hence, the intersection co-ordinates is (0, -13/3) Ans.
14. Find the value of ** [3]
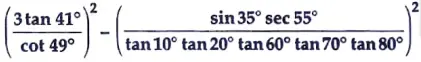
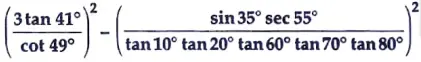
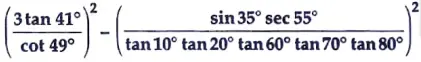
15. Two spheres of same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere.** [3]
16. Find the ratio in which the line x – 3y = 0 divides the line segment joining the points (-2,-5) and (6, 3). Find the coordinates of the point of intersection. [3]
Sol. Let required ratio be k : 1
By section formula, we have
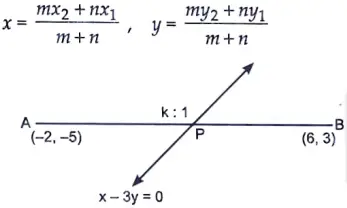


Here, x1 = -2, x2 = 6, y1 = -5, y2 = 3
m = k, n = 1
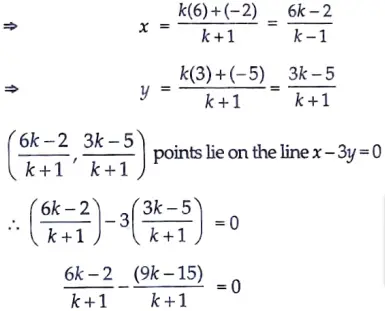
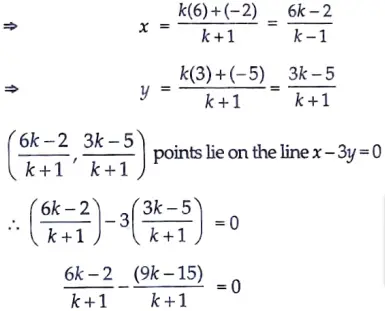
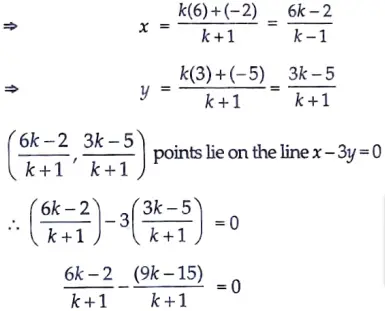
6k – 2 – 9k + 15 = 0
-3k + 13 = 0
k = 13/3
Hence required ratio is
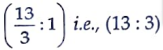
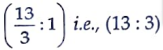
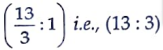
Here, intersection point are,
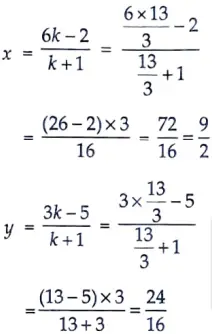
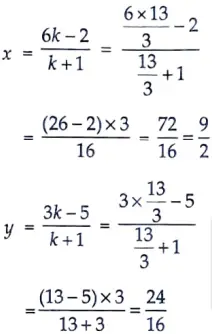
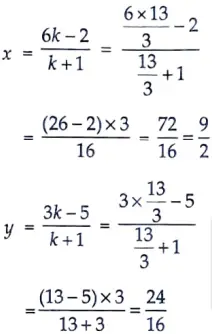
= 3/2
∴ intersection point is (9/2, 3/2) Ans.
17. Evaluate :** [3]
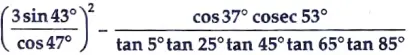
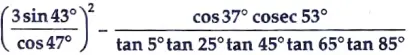
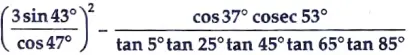
18. In Figure 4, a square OABC is inscribed in a quadrant OPBQ. If OA = 15 cm, find the area of the shaded region. (Use 𝛑 = 3.14)
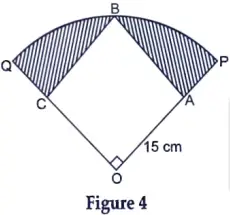


Sol. Given, OABC is a square with OA = 15 cm
OB = radius = r
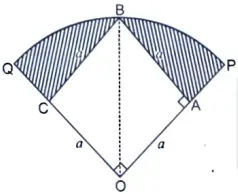


Let side of square be a then,
a2 + a2 = r2
2a2 = r2
r = √2a
r = 15√2 cm (∵ a = 15 cm)
Area of square = Side x Side
= 15 x 15
= 225 cm2
Area of quadrant OPBQ
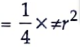
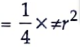
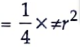
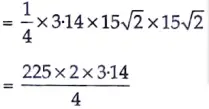
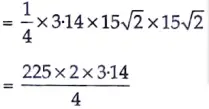
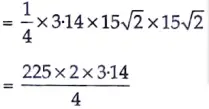
= 225 x 1.57
= 353.25 cm2
Area of shaded region
= Area of quadrant OPBQ – Area of square OABC
=353.25 – 225
= 128.25 cm²
OR
In Figure 5, ABCD is a square with side 2√2 cm and inscribed in a circle. Find the area of the shaded region. (Use 𝛑 = 3.14)
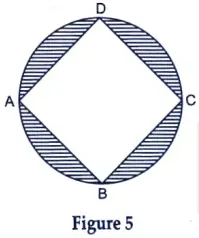


Sol. Given, ABCD is a square with side 2√2 cm
∵ BD = 2r


In ∆BDC
BD2 = DC2 + BC2
4r2 = 2(DC)2
(∵ DC = CB = Side = 2√2 )
4r2 = 2 x 2√2 x 2√2
4r2 = 8 x 2
4r2 = 16
⇒ r2 = 4
r = 2 cm
Area of square BCDA = Side x Side
= DC x BC
= 2√2 x 2√2
= 8 cm2
Area of circle = 𝛑r2
= 3.14 x 2 x 2
= 12.56 cm2
Area of shaded region
= Area of circle – Area of square.
= 12.56 – 8
= 4.56 cm2 Ans.
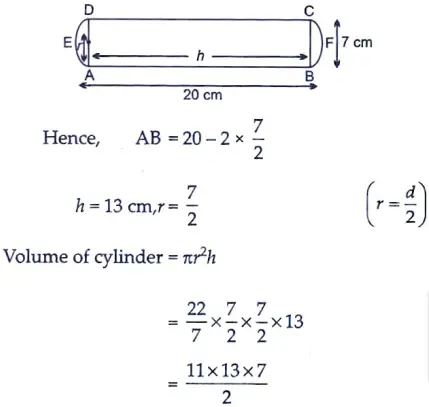
19. A solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 20 cm and the diameter of the cylinder is 7 cm. Find the total volume of the solid. (Use 𝛑 = 22/7) [3]
Sol. ABCD is a cylinder and BFC and AED are two hemisphere which has radius (r) = 7/2 cm


= 1001/2
= 500.5 cm3
Volume of two hemisphere
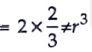
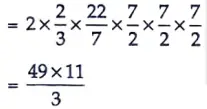
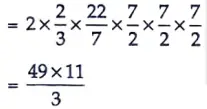
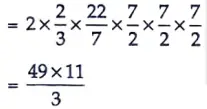
= 539/3
= 179.67 cm3
Total volume of solid = Volume of two hemisphere + Volume of cylinder
= 179.67 + 500.5
= 680.17 cm3 Ans.
20. The marks obtained by 100 students in an examination are given below: [3]
| Marks | Number of Students |
| 30 – 35 | 14 |
| 35 – 40 | 16 |
| 40 – 45 | 28 |
| 45 – 50 | 23 |
| 50 – 55 | 18 |
| 55 – 60 | 8 |
| 60 – 65 | 3 |
Find the mean marks of the students.
Sol.
| Marks | Number of Students | xi | fixi |
| 30 – 35 | 14 | 32.5 | 455 |
| 35 – 40 | 16 | 37.5 | 600 |
| 40 – 45 | 28 | 42.5 | 1190 |
| 45 – 50 | 23 | 47.5 | 1092.5 |
| 50 – 55 | 18 | 52.5 | 945 |
| 55 – 60 | 8 | 57.5 | 460 |
| 60 – 65 | 3 | 62.5 | 187.5 |
| 𝚺fi = 110 | 𝚺fixi = 4930 |
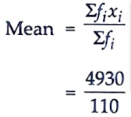
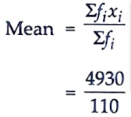
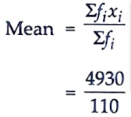
= 44.82 Ans.
21. For what value of k, is the polynomial [3]
f(x) = 3x4 – 9x3 + x2 + 15x + k
completely divisible by 3x2 – 52**
OR
Find the zeroes of the quadratic polynomial 7y2 – 11/3y – 2/3 and verify the relationship between the zeroes and the coefficients.
Sol. The given polynomial is
P(y) = 7y2 – 11/3y – 2/3
∵ P(y) = 0
7y2 – 11/3y – 2/3 = 0
⇒ 21y2 – 11y – 2 = 0
⇒ 21y2 – 14y + 3y – 2 = 0
⇒ 7y (3y – 2) + 1 (3y – 2) = 0
⇒ (3y – 2) (7y + 1) = 0
∴ y = 2/3, – 1/7
So zeroes of P(y) are 2/3, – 1/7 Ans.
Verification : On comparing 7y – 11/3y – 2/3
with ax2 + bx + c, we get
a = 7, b = 11/3, c = 2/3
Sum of zeroes = -b/a
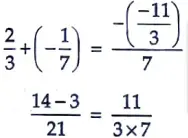
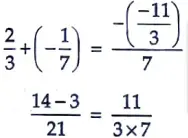
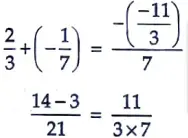
11/21 = 11/21
Product of zeroes = c/a
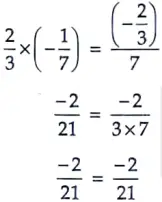
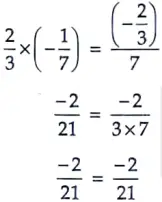
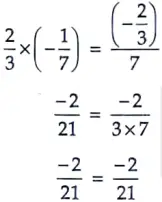
Hence Verified.
22. Write all the values of p for which the quadratic equation x2 + px + 16 = 0 has equal roots. Find the roots of the equation so obtained. [3]
Sol. Given, equation is x2 + px + 16 = 0
This is of the form ax2 + bx + c = 0
where, a = 1, b = p and c = 16
∴ D = b2 – 4ac
= p2 – 4 x 1 x 16
= p2 – 64
for equal roots, we have
D = 0
p2 – 64 = 0
p2 = 64
p = ± 8
Putting p = 8 in given equation we have,
x2 + 8x + 16 = 0
(x – 4)2 = 0
x = 4, 4
∴ Required roots are -4 and -4 or 4 and 4. Ans.
SECTION – D
23. In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then prove that the angle opposite the first side is a right angle [4]
24. From a point P on the ground, the angle of elevation of the top of a tower is 30° and that of the top of the flag-staff fixed on the top of the tower is 45°. If the length of the flag-staff is 5 m, find the height of the tower. (Use √3 = 1732) [4]
Sol. Let AB be the tower and BC be the flag-staff.
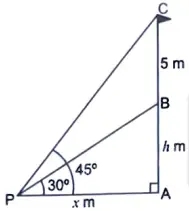


Let P be a point on the ground such that ∠APB = 30° and ∠APC = 45°, BC = 5 m
Let AB = h m and PA = x metres
From right ∆PAB, we have
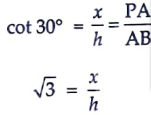
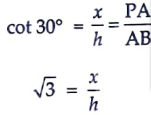
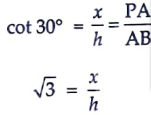
⇒ x = √3 h …..(i)
From right ∆PAC, we have
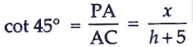
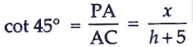
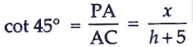
x = h + 5 …..(ii)
Equating the values of x from equations (i) and (ii), we get
√3 h = h + 5
√3h – h = 5
h(√3 – 1) = 5
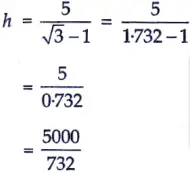
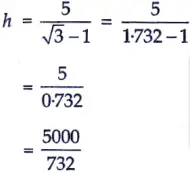
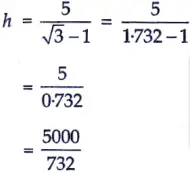
= 6.83 m
Hence, the height of tower is 6.83 m Ans.
25. A right cylindrical container of radius 6 cm and height 15 cm is full of ice-cream, which has to be distributed to 10 children in equal cones having hemispherical shape on the top. If the height of the conical portion is four times its base radius, find the radius of the ice-cream cone. [4]
Sol. Let Rand H be the radius and height of cylinder.
Given, R = 6 cm, H = 15 cm.
Volume of ice-cream in the cylinder = 𝛑R2H
= 𝛑 x 36 x 15
= 540 𝛑 cm3
Let the radius of cone be r cm
Height of the cone (h) = 4r
Radius of hemispherical portion = r cm.
∴ Volume of ice-cream cone = Volume of cone + Volume of hemisphere
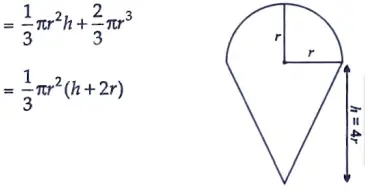


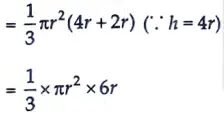
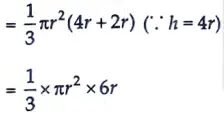
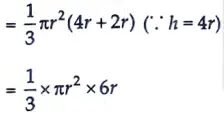
= 2𝛑r3
Number of ice cream cones distributed to the children = 10
⇒ 10 x Volume of ice-cream in each cone = Volume of ice-cream in cylindrical container
⇒ 10 x 2𝛑r3 =540𝛑
⇒ 20r3 = 540
⇒ r3 = 27
r = 3
Thus, the radius of the ice-cream cone is 3 cm. Ans.
26. Construct an equilateral ∆ABC with each side 5 cm. Then construct another triangle whose sides are 2/3 times the corresponding sides of ∆ABC.** [4]
OR
Draw two concentric circles of radii 2 cm and 5 cm. Take a point P on the outer circle and construct a pair of tangents PA and PB to the smaller circle. Measure PA.**
27. Change the following data into less than type’ distribution and draw its ogive : [4]
| Class Interval | Frequency |
| 30-40 | 7 |
| 40-50 | 5 |
| 50-60 | 8 |
| 60-70 | 10 |
| 70-80 | 6 |
| 80-90 | 6 |
| 90-100 | 8 |
Sol.
| Class Interval | Frequency |
| less than 40 | 7 |
| less than 50 | 12 |
| less than 60 | 20 |
| less than 70 | 30 |
| less than 80 | 36 |
| less than 90 | 42 |
| less than 100 | 50 |
On graph paper, we take the scale.
28. Prove that: [4]
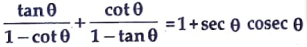
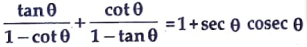
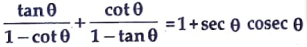
Sol.
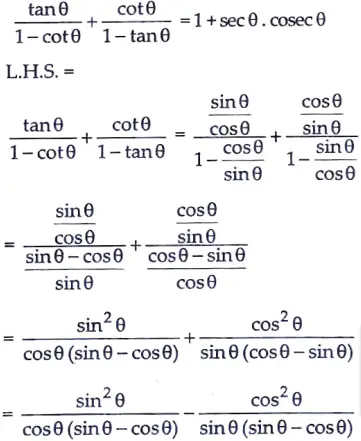





Hence Proved.
OR
Prove that :
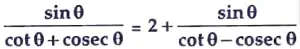
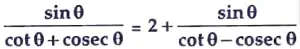
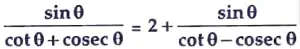
Sol. LH.S.



R.H.S.
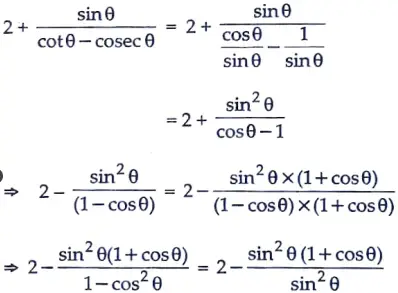
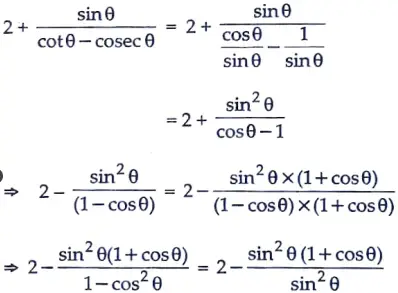
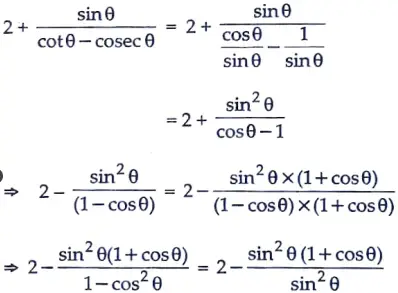
= 2 – (1 + cos 𝜃)
= 1 – cos 𝜃 …..(i)
From equation (i) and (ii), we get
L.H.S. = R.H.S. Hence Proved.
29. Which term of the Arithmetic Progression -7, – 12, – 17, – 22, …. will be – 82? Is – 100 any term of the A.P. ? Give reason for your answer. [4]
Sol. -7, -12, -17, -22, ….
Here a = -7, d = -12 – (-7)
= -12 + 7
= -5
Let Tn = -82
∴ Tn = a + (n – 1) d
– 82 = -7 + (n – 1)(-5)
– 82 = -7 – 5n + 5
– 80 = -5n
n = 16
Therefore, 16th term will be – 82.
Let Tn = -100
Again, Tn = a + (n – 1) d
– 100 = -7 + (n – 1) (-5)
– 100 = -7 -5n + 5
– 98 = -5n
n = 98/5
But the number of terms can not be in fraction. So, – 100 can not be a term of this A.P. Ans.
OR
How many terms of the Arithmetic Progression 45, 39,33, ….. must be taken so that their sum is 180? Explain the double answer.
Sol. 45, 39, 33, ……..
Here a = 45, d = 39 – 45 = -6
Let Sn = 180
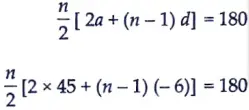
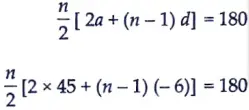
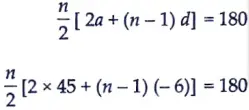
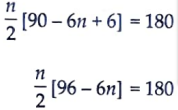
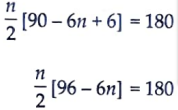
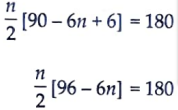
n (96 – 6n) = 360
96n – 6n2 = 360
6n2 – 96n + 360 = 0
On dividing the above equation by 6
n2 – 16n + 60 = 0
n2 – 10n – 6n + 60 = 0
n(n – 10) – 6(n -10) = 0
(n – 10) (n – 6) = 0
n = 10, 6
∴ Sum of first 10 terms = Sum of first 6 terms
= 180
This means that the sum of all terms from 7th to 10th is zero. Ans.
30. In a class test, the sum of Arun’s marks in Hindi and English is 30. Had he got 2 marks more in Hindi and 3 marks less in English, the product of the marks would have been 210. Find his marks in the two subjects. [4]
Sol. Let Arun marks in Hindi be x and marks in English be y.
Then, according to question, we have
x+ y = 30 …..(i)
(x + 2) (y – 3) = 210 …..(ii)
from equation (i), put x = 30 – y in equation (ii)
(30 – y + 2) (y – 3) = 210
(32 – y) (y – 3) = 210
32y – 96 – y2 + 3y = 210
y2 – 35y + 306 = 0
y2 -18y – 17y + 306 = 0
y (y – 18) – 17 (y – 18) = 0
(y – 18) (y – 17) = 0
y = 18, 17
Put y = 18 and 17 in equation (i), we get
x = 12, 13
Hence his marks in Hindi can be 12 and 13 and in English his marks can be 18 and 17. Ans.