Are you an AKTU B.Tech student who is failing to grasp the complexities of Curves in Surveying and Geomatics? Look no farther than our in-depth guide, which includes key questions and answers. Whether you’re preparing for an exam or just brushing up on your knowledge, this resource is a must-read for every student hoping to grasp this difficult topic.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Surveying And Geomatics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. What is curve? Why these are needed and also give a classification?
Ans. A. Curves: These are arcs with a limited radius that are placed between intersecting straights to progressively negotiate a direction shift.
B. Necessity: These are necessary due to following reasons:
- 1. By including curves, it is possible to gradually adjust the gradient, direction, or alignment.
- 2. Curves are provided to give the passengers comfort.
- 3. Curves are offered so that turning on a road or track is simple.
C. Classification of Curves:
1. Horizontal Curves: These are the curves provided to negotiate a change in direction. These can be further classified:
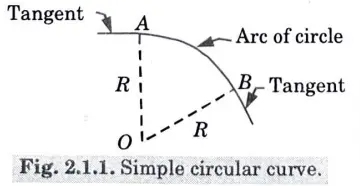
i. Simple Circular Curve: A single circle arc makes up a straightforward circular curve. According to Fig., it is tangential to both of the route’s straight lines.


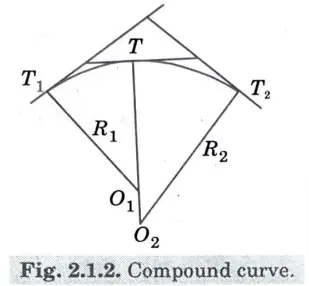
ii. Compound Curve: As seen in Fig., compound curves are made up of two or more simple circular curves with various radii that come together at a common tangent point T.


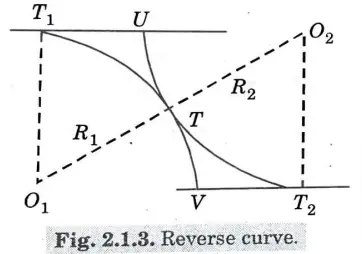
iii. Reserve Curve: Reverse curves are formed when two straight, equal-radius circular curves with opposite curvature directions unite to produce an S-shaped curve, as shown in FIG.


2. Transition Curve: It is a curve that is offered between a straight and a simple circular curve, and whose radius alternates between infinite and finite (equivalent to the radius of the simple circular curve) or vice versa.
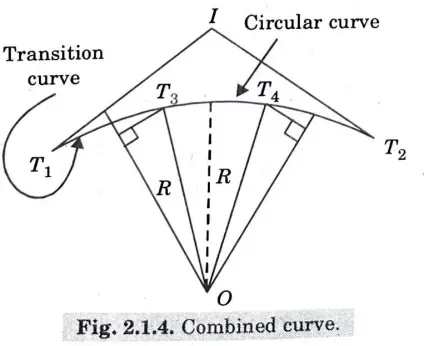
3. Combined Curve: A combined curve, as seen in Fig., is made up of a circular curve and a transition curve.


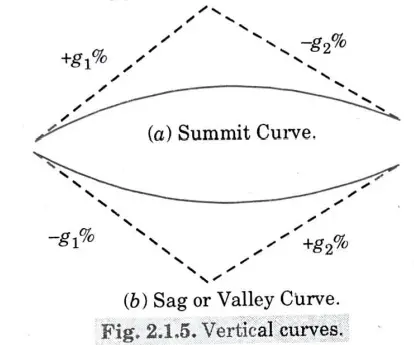
4. Vertical Curve: These are the curves offered to adjust the longitudinal slope of a gradient smoothly.Vertical curves are further of two types:
i. Summit Curve: It is available whenever a rising gradient crosses a decreasing gradient, or when the two straights come together to form a summit as seen in Fig. a.
ii. Sag or Valley Curve: Sag curves are created when two straight lines meet and produce a valley or sag, or when a descending gradient meets a rising gradient.


Q2. Two straight AI and BI meet at a chainage of 3450 m. A right handed simple circular curve of 250 m radius joins them. The deflection angle between the two straight is 50 °. Tabulate the necessary data to layout the curve by Rankine’s method of deflection angles. Take the chord interval 20 m.
Ans. Given: Radius of curve, R = 250 m, Deflection angle, ∆ = 50 °
Chord interval = 20 m, Chainage of meeting point = 3450m
To find: Layout of curve.






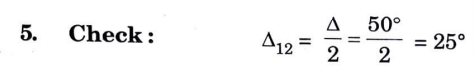
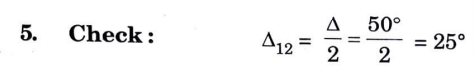
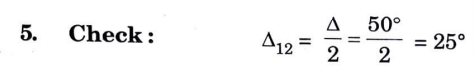
Q3. What is vertical curve and its type?
Ans. A. Vertical Curves :
- 1. A curve in the vertical plane, known as a vertical curve, connects two separate gradients when they cross at a point.
- 2. Parabolic curves are preferred because determining the shortest sight distance is simple.
B. Types of Vertical Curves: Following are two types of vertical curve:
1. Summit or convex Curve :
- i. If a vertical curve has its convexity upward, it is called a summit curve.
- ii. Depending upon the field condition a summit curve may be formed :
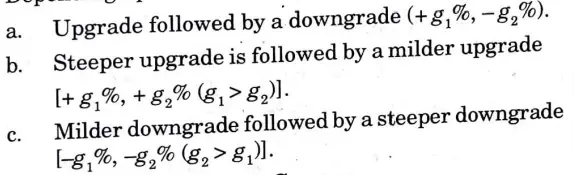
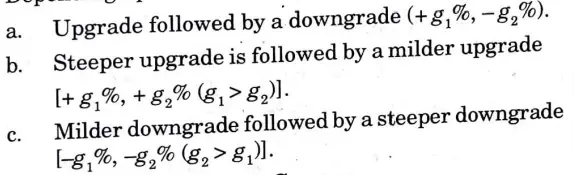
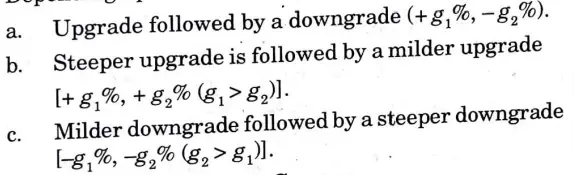
2. Valley Sag or Concave Curve :
i. A sag or valley curve is a vertical curve that is convex in the descending direction or concave in the upward direction.
ii. A sag curve may be formed :
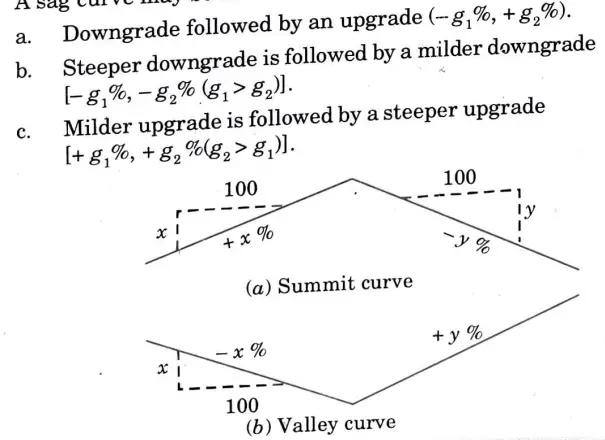


Q4. A vertical curve lies between two gradients of + 0.60 % and.- 0. 9 %. Rate of change of gradients is to be 0.075 % per 30 m. If the elevation and chainage of point of intersection is 1430 m and 985.5 m respectively. Find the chainage of the tangent points and apex of the curve.
Ans. Given: grades g1 and g2 + 0.60 % and -0.9 %, Rate of change of gradient= 0.075% / 30m, Elevation = 1430 m, Chainage = 985.5 m
To Find: Chainage of the tangent points, Apexof curve



2. The curve midpoint will be the apex of the curve. Chainage of apex of the curve is the chainage of point of intersection i.e., 1430 m.
3. Chainage of the two tangent points will be (985.50 – 300) and (985.50 + 300) = 685.5 m and 1285.5 m.
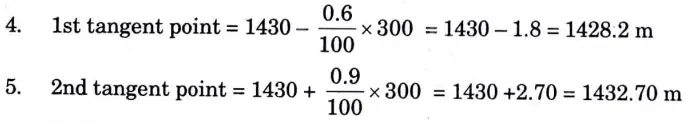
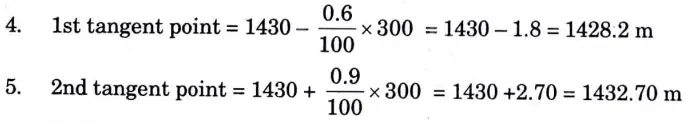
Q5. Write a short note on superelevation or cant.
Ans. A. Superelevation or Cant :
- 1. To mitigate the effects of the centrifugal force, superelevation involves raising the outer border of a road or rail route on a curve.
- 2. When a vehicle travels along a curved path, a force known as the centrifugal force P pushes against it horizontally through the vehicle’s centre of gravity G in a direction away from the curve’s centre, as shown in Fig. 2.18.1.
- 3. In addition to the vehicle’s weight W, this force exists.
- 4. The vehicle is frequently pushed off the road or track by the force P.
- 5. The outside border of the road or the outer rail on railroads is raised above the inner one to counteract this effect.
- 6. Superelevation or cant refers to the variation between the top levels of the outer and inner edges or rails.
- 7. The radius of the curve and the average speed of the cars determine the amount of raising.
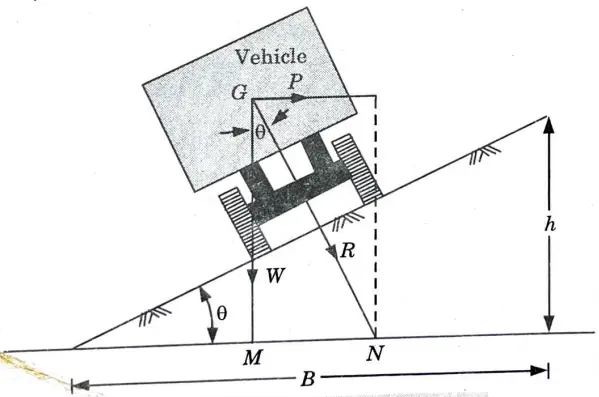


- 8. From mechanics, centrifugal force P is given by,



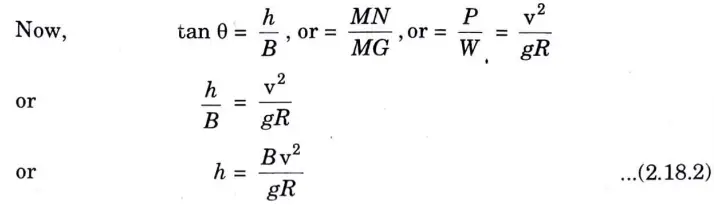
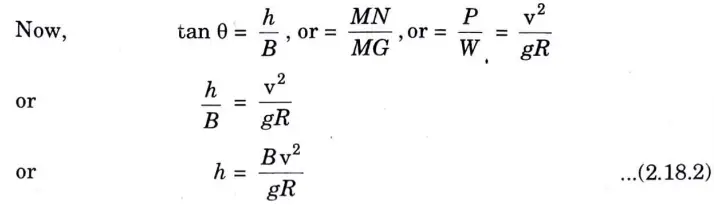
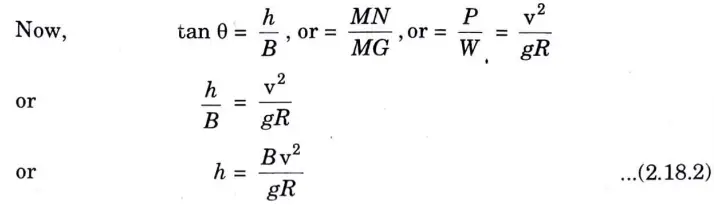
In Eq. (2. 18.2), B is the horizontal distance between the two edges of a highway or the gauge of the railway track.
Q6. Two straight lines AC and CB intersect at C, at a chainage of 86.22 chains at a deflection angle of 62°. These lines are to be smoothly connected by a simple curve of radius 12 chains. Find the tangent length, length of the curve and the chainages of the starting and end points of the curve. Find also the length of the long chord.
Ans. Given: Deflection angle, ∆ = 62°, Radius, R = 12 chain
To Find : Tangent length, length of curve, chainage at be starting and end points, length of long chord.
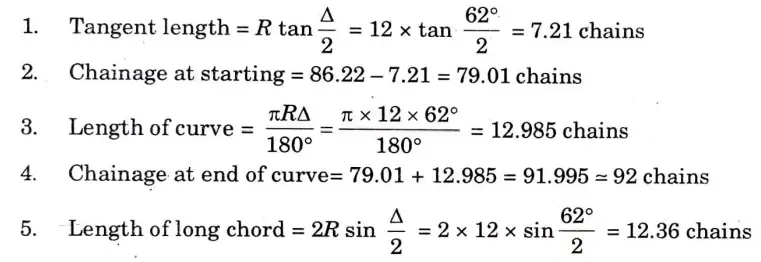
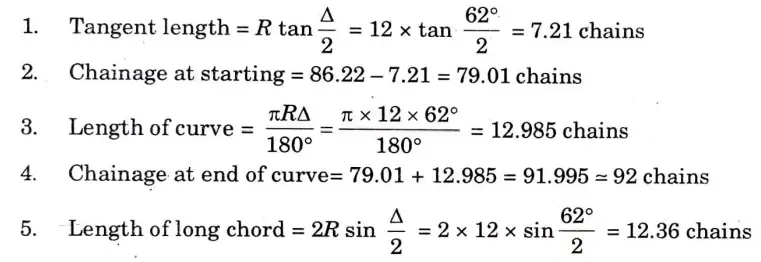
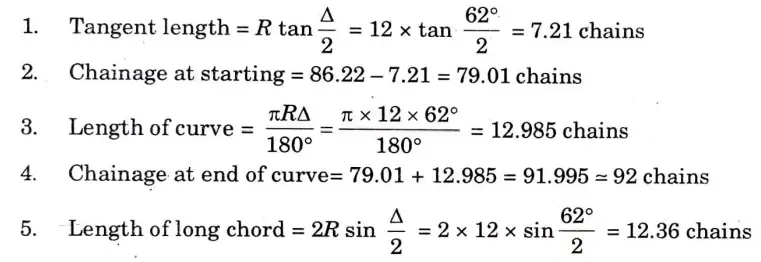



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Surveying And Geomatics Quantum, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Surveying And Geomatics Quantum PDF: | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |

1 thought on “Unit 02 : (CURVES) Surveying And Geomatics AKTU Btech”