Discrete Structure Unit 5 Btech TREES, GRAPHICS, AND COMBINATORICS Tree topologies, graph theory, algorithms, counting principles, permutations, combinations, and binomial coefficients are all investigated by AKTU. Learn about their importance in computer science and network analysis.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Discrete Structures and Theory of Logics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. Explain the following terms:
- i. Tree
- ii. Forest
- iii. Binary tree
- iv. Complete binary tree
- v. Full binary tree
Ans.
i. Tree:
- 1. A tree is a connected graph that contains no cycle or circuit. It is a simple graph having no self loop or parallel edges.
- 2. A tree contains a finite set of elements which are called vertices or nodes. The vertex can have minimum degree 1 and maximum degree n.
- 3. The number of vertices in a tree is called order of tree.
- 4. A tree with only one vertex is called trivial or degenerate or empty tree.
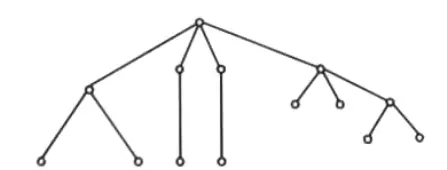


ii. Forest: A forest is a collection of disjoint tree. It is an undirected, disconnected, acyclic graph.



iii. Binary tree:
- 1. Binary tree is the tree in which the degree of every node is less than or equal to
- 2. A tree consisting of no nodes is also a binary tree.
iv. Complete binary tree: A binary tree is said to be complete binary tree if all its levels, except the last, have maximum number of possible nodes (i.e., 2), and if all the nodes at the last level appear as far left as possible.


It is represented as Tn where n is number of nodes.
v. Full binary tree: A binary tree is said to be extended or full binary tree if each node has either 0 or 2 children.


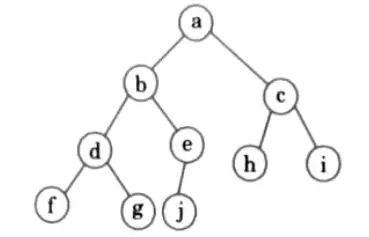
Q2. Explain in detail about the binary tree traversal with an example.
Ans. Tree traversal: A traversal of tree is a process in which each vertex is visited exactly once in a certain manner. For a binary tree we have three types of traversal :
1. Preorder traversal : Each vertex is visited in the following order :
- a Visit the root (N).
- b. Visit the left child (or subtree) of root (L).
- c. Visit the right child (or subtree) of root (R).
2 Postorder traversal:
- a. Visit the left child (subtree) of root. .
- b. Visit the right child (subtree) of root.
- c. Visit the root.
3. Inorder traversal:
- a. Visit the left child (subtree) of root.
- b. Visit the root.
- c. Visit the right child (subtree) of root
A binary tree with 12 vertices:
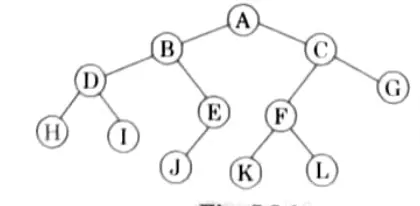


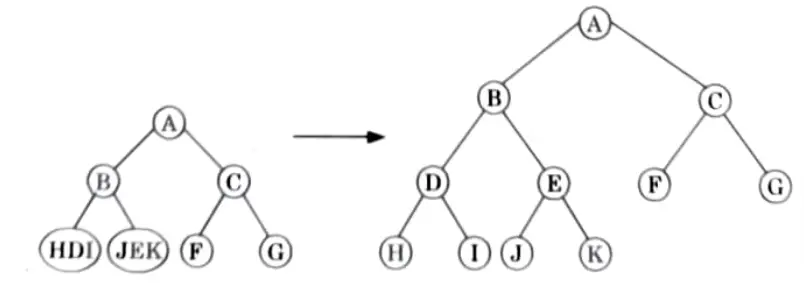
Q3. Define a binary tree. A binary tree has 11 nodes. It’s inorder and preorder traversals node sequences are:
Preorder :A B D H I E J L C F G
Inorder: H D I B J E K A F C G G
Draw the tree.
Ans. Binary Tree:
- 1. Binary tree is the tree in which the degree of every node is less than or equal to
- 2. A tree consisting of no nodes is also a binary tree.
Numerical:
Step 1: n preorder sequence, leftmost element is the root of the tree. By searchingA in ‘Inorder Sequence’ we can find out all the elements on the left and right sides of ‘A’.
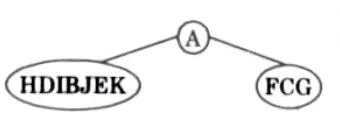


Step 2: We recursively follow the above steps and we get


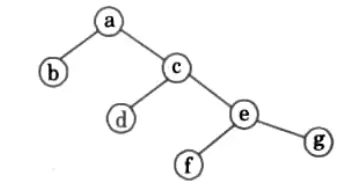
Q4. Given the inorder and postorder traversal of a tree T:
Inorder: HFEABIGDC
Postorder : BEHFACDGI
Determine the tree T and it’s Preorder.
Ans. The root of tree is I.



Now elements on right ofI are D, G, C and G comes last of all in postorder traversal.
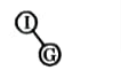


Now D and C are on right of G and D comes last of G and I postorder traversal so
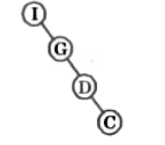


Now element left ofI are H FEA B in inorder traversal and A comes last of all in postorder traversal. Therefore tree will be
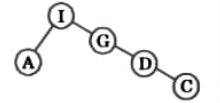


Now H F E are on left of A in inorder traversal and B comes last of all and continuing in same manner. We will get final binary tree as



Preorder traversal of above binary tree is CAFHEBDGI
Q5. Draw a binary search tree by inserting following integers 55, 20, 63, 10, 28, 60, 93, 5, 11, 40, 68, 25.
Ans.



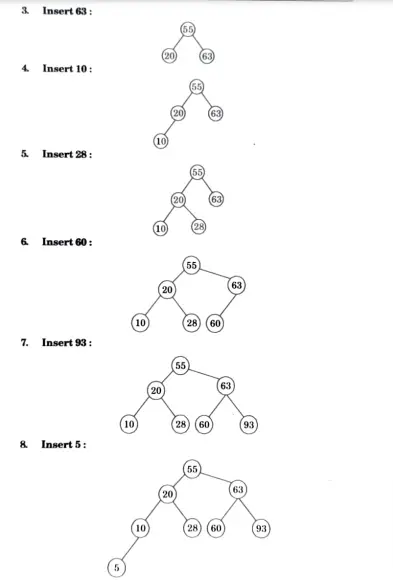


Q6. Write a short note on graph coloring
- Ans.
1. Suppose that G (V, E) is a graph with no multiple edges, a vertex colouring of G is an assignment of colours. - 2. A graph G is m-colourable if there exists a colouring of G which uses m colours.
- 3. Proper colouring refers to colouring the vertices so that no two adjacent vertices have the same colour. Improper colouring refers to colouring the vertices in any other way.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Discrete Structures and Theory of Logics Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Discrete Structures and Theory of Logics Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
