Unit 3 of Discrete Structure for Btech AKTU’s “LATTICES & BOOLEAN ALGEBRA” investigates lattices, Boolean algebra, and its applications, including lattice theory, operations, and logic circuits.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Discrete Structures and Theory of Logics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. Explain types of lattice.
Ans. Types of lattice:
1. Bounded lattice: A lattice L is said to be bounded if it has a greatest element 1 and a least element 0. In such lattice we have



2. Complemented lattice: Let L be a bounded lattice with greatest element l and least element 0. Let a ∈ L then an element a’ ∈ L is complement of a if,
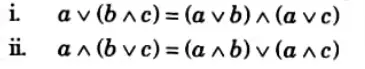
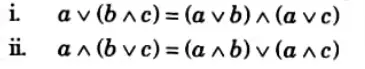
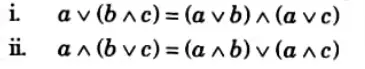
A lattice L is called complemented if is bounded and if every element in L has a complement.
3. Distributive lattice: A lattice L is said to be distributive if for any element a, b and c of L following properties are satisfied :
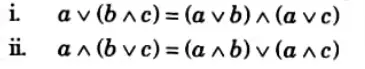
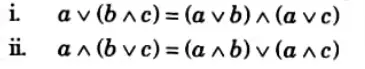
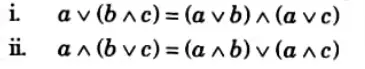
otherwise L is non-distributive lattice.
4. Complete lattice: A lattice L is called complete if each of its nonempty subsets has a least upper bound and greatest lower bound.
For example:



Q2. If the lattice is represented by the Hasse diagram given below:
- i. Find all the complements of ‘e’.
- ii. Prove that the given lattice is bounded complemented lattice.
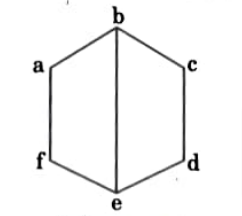


Ans. i. Complements of e are c and d which are as follows:
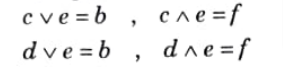
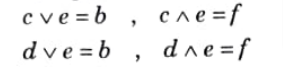
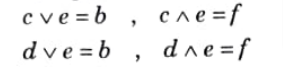
ii. A lattice is bounded if it has greatest and least elements. Here b is greatest and f is least element.
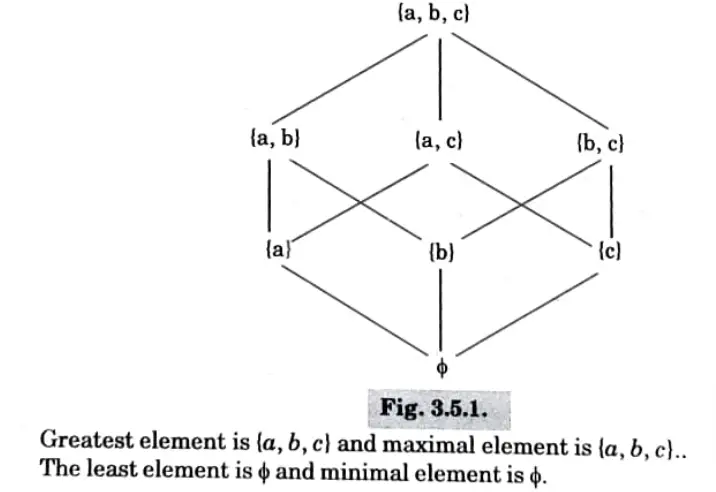
Q3. Let L be a bounded distributed lattice, prove if a complement exists, it is unique. Is D12 a complemented lattice ? Draw the Hasse diagram of [P (a,b,c), ≤ ] (Note: ‘≤’ stands for subset). Find greatest element, least element, minimal element and maximal element.
Ans.








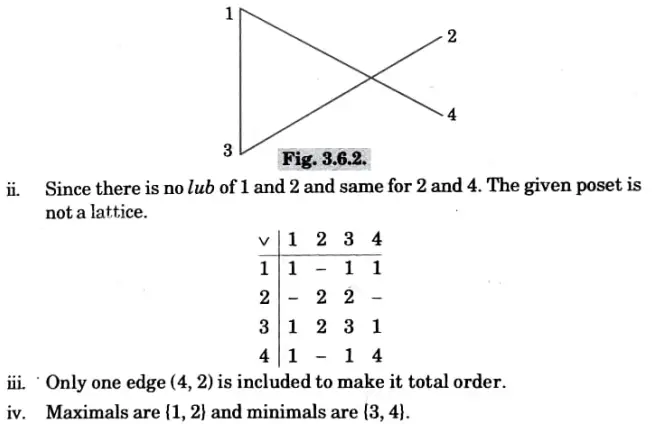
Q4. The directed graph G for a relation R on set A = {1,2,3, 4) is shown below :
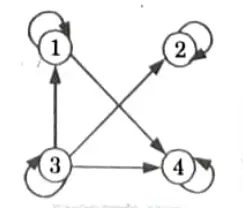


i. Verify that (A, R) is a poset and find its Hasse diagram.
ii. Is this a lattice ?
iii. How many more edges are needed in the Fig. to extend (A, R) to a total order?
iv. What are the maximal and minimal elements ?
Ans.





Q5. a. Prove that every finite subset of a lattice has an LUB and a GLB.
b. Give an example of a lattice which is a modular but not a distributive.
Ans. a. 1. The theorem is true if the subset has 1 element, the element being its own glb and lub.
2. It is also true if the subset has 2 elements.
3. Suppose the theorem holds for all subsets containing 1, 2, .., k elements, so that a subset a, G2, .., G of L has a glb and a lub.
4. If L contains more than k elements, consider the subset



12. IfL is finite and contains m elements, the induction process stops when k +1 =m.
b. 1. The diamond is modular, but not distributive.
2. Obviously the pentagon cannot be embedded in it.
3. The diamond is not distributive:



4. Each sublattice of a distributive lattice is a separate distributive lattice, and the distributive lattices are closed under them.
5. The lattice is not distributive if the diamond can be embedded in it because it has a sublattice that is not distributive.
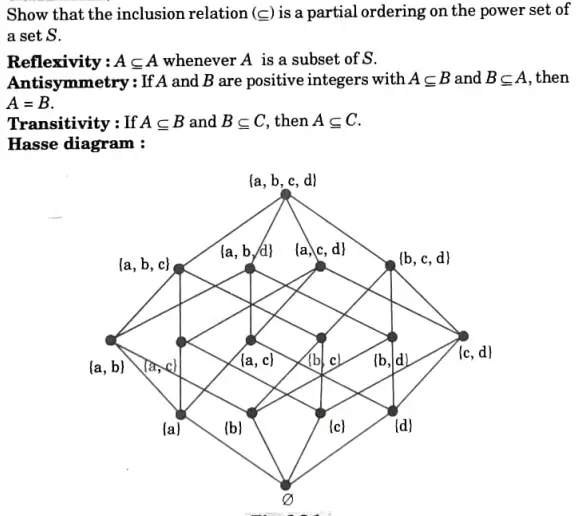
Q6. Show that the inclusion relation ⊆ is a partial ordering on the power set of a set S. Draw the Hasse diagram for inclusion on the set P(S), whereS= {a, b, c, d}. Also determine whether (P(S), ⊆) is a lattice.
Ans.








Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Discrete Structures and Theory of Logics Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Discrete Structures and Theory of Logics Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
