Unit 2 of “ALGEBRAIC STRUCTURES” in Btech Discrete Structure AKTU investigates groups, rings, and fields, as well as their characteristics and applications.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Discrete Structures and Theory of Logics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. What is algebraic structure ? List properties of algebraic system.
Ans. Algebraic structure: A non-empty set G with one or more binary operations is an algebraic structure. Assume that the binary operation * on G. If so, the structure (G, *) is algebraic.



Q2. Show that the set G = {x + y √2 |x,y ∊ Q} is a group with respect to addition.
Ans.
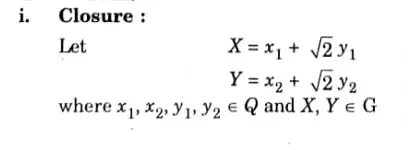
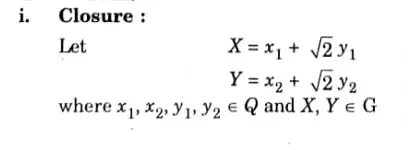
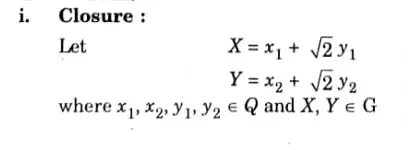






Q3. Prove that (Z6, (+6)) is an abelian group of order 6, where Z6={0,1,2, 3, 4, 5}.
Ans. The composition table is:
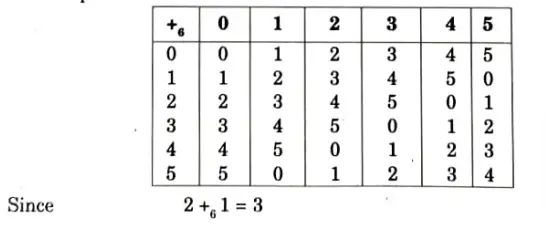


4 + 65 = 3
From the table we get the following observations
Closure: Since all the entries in the table belong to the given set Z6. Therefore, Z6 is closed with respect to addition modulo 6.
Associativity: The composition ‘+6’ is associative. If a, b, c are any three elements of Z6,
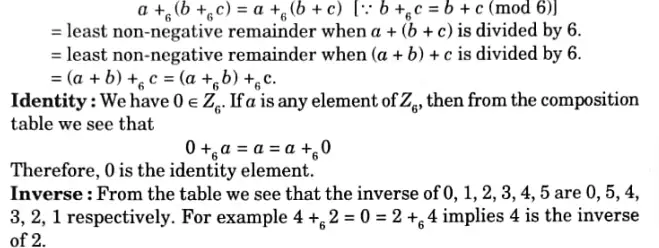
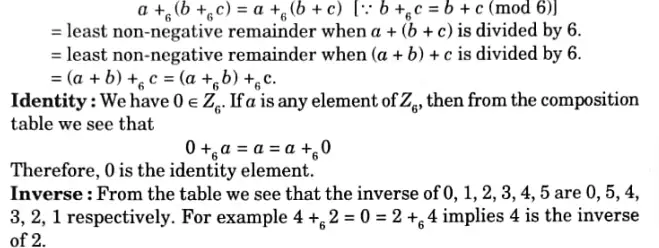
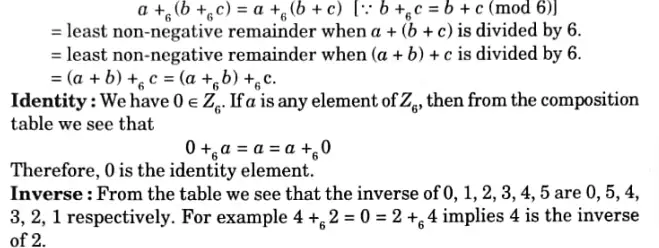
Commutative: The composition is commutative as the elements are symmetrically arranged about the main diagonal. The number of elements in the set Z6 is 6.
∴(Z6 + 6) is a finite abelian group of order 6.
Q4. Let G = {1, – 1, i, – i} with the binary operation multiplication be an algebraic structure, where i = √-1. Determine whether G is an abelian or not.
Ans. The composition table of G is
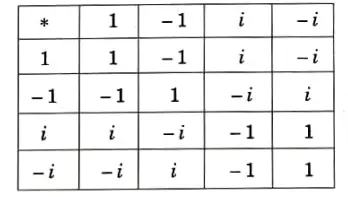


1. Closure property: Since all the entries of the composition table are the elements of the given set, the set G is closed under multiplication.
2. Associativity: Complex numbers make up the components of G, and we are aware that their multiplication is associative.
3. Identity: Here, 1 is the identity element.
4. Inverse: From the composition table, we see that the inverse elements of 1,-1, i,-i are 1,-1,-i, i respectively.
5. Commutativity: The table’s related rows and columns have the same contents. The binary operation is hence commutative. As a result, the group (G, *) is abelian.
Q5. Let G be a group and let a, b ∊ G be any elements.
Then
i. (a-1)-1 = a
ii. (a * b)-1 * a-1.
Ans.



Q6. Prove that the intersection of two subgroups of a group is also subgroup.
Ans.
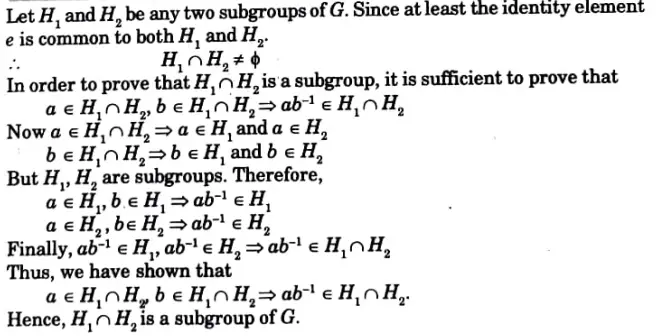
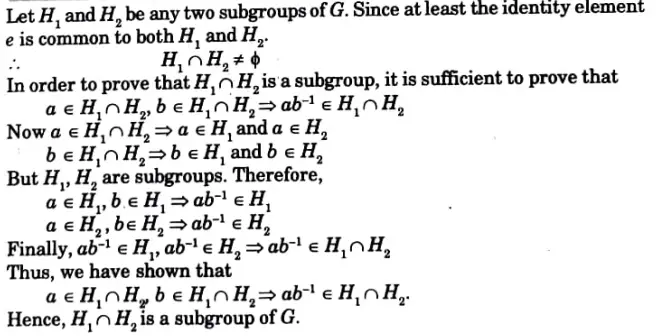
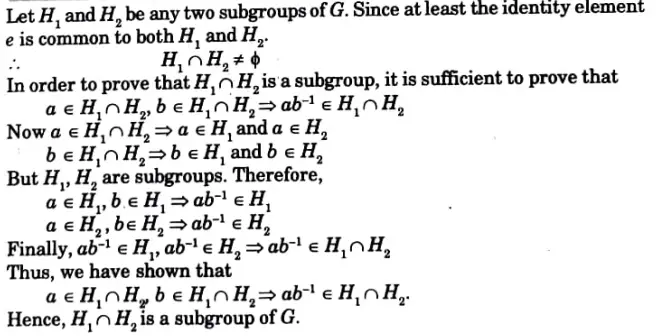



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Discrete Structures and Theory of Logics Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Discrete Structures and Theory of Logics Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |

3 thoughts on “UNIT – 2 : ALGEBRAIC STRUCTURES in Discrete structure Btech AKTU”