SETS, FUNCTIONS, AND NATURAL NUMBERS UNIT 01 in Discrete Structures Btech AKTU covers sets, functions, and natural numbers. Set operations, properties, function types, and applications are all included. Students will find this useful.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Discrete Structures and Theory of Logics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. What do you mean by multisets ?
Ans.
1. Multisets are sets where an element appear more than once,
For example: A = {1, 1, 1, 2, 2, 3}
B = {a, a, a, b, b, b, c, c}
are multisets.
2. The multisets A and B can also be written as
A = {3.1, 2.2, 1.3} and B = {3.a, 3.b, 2.c}
3. The multiplicity of an element in a multiset is defined to be the number of times an element appears in the multiset. In above examples, multiplicities of the elements 1,2,3 in multiset A are 3,2, 1 respectively.
4. Let A and B be two multisets. Then, A ◡ B, is the multiset where the multiplicity of an element is the maximum of its multiplicities in A and B.
5. The intersection of A and B, A റ B, is the multiset where the multiplicity of an element is the minimum of its multiplicities in A and B.
6. The difference between A and B, abbreviated as A-B, is the multiset whose multiplicity, if positive, equals the multiplicity of an element in A less the multiplicity of an element in B, and, if negative and zero, equals zero.
7. The sum of A and B, A + B, is the multiset where the multiplicity of an elements is the sum of multiplicities of the elements in A and B.
Q2. Prove for any two sets A and B that, (A ◡ B) = A’റB’.
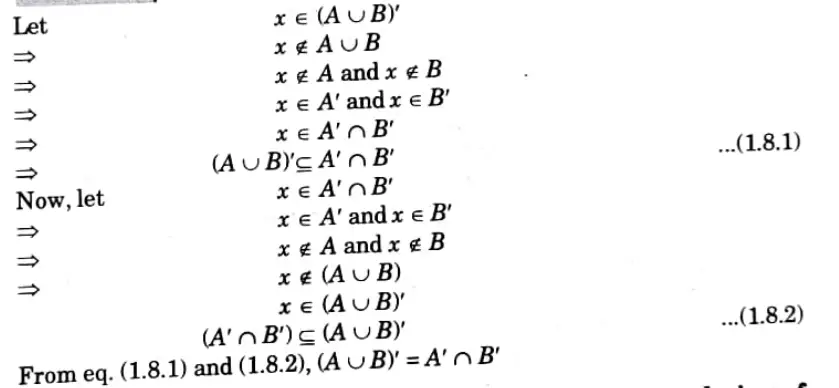
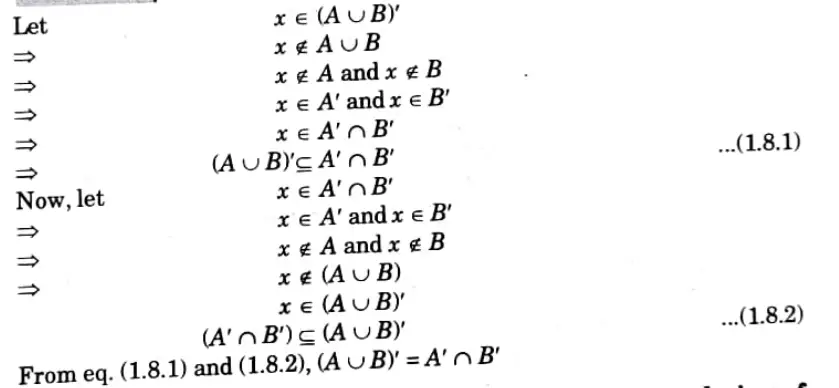
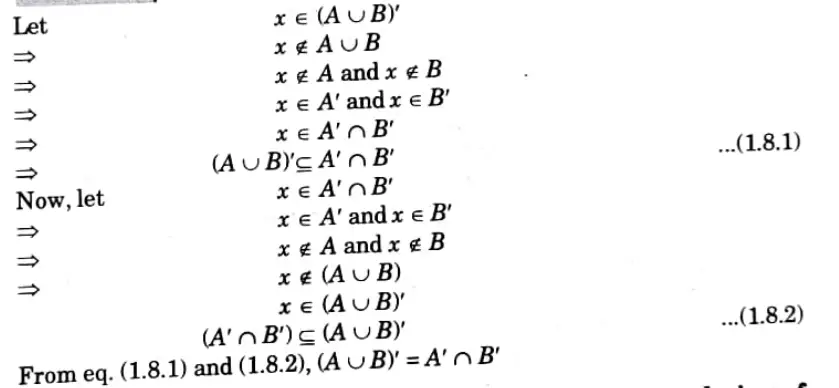
Q3. If A and B are two subsets of universal set, then prove the following:
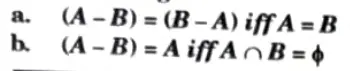
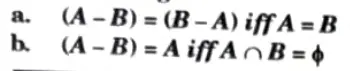
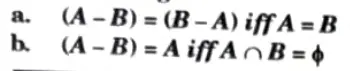
Ans.



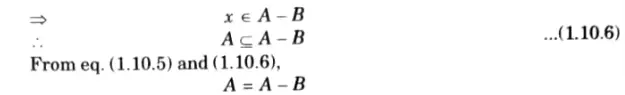
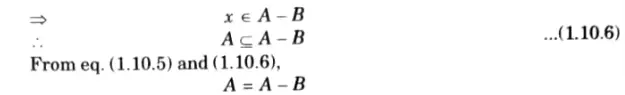
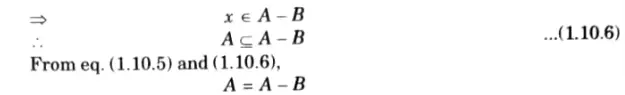
Q4. Explain operation on relation with example.
Ans. 1. Since relations are collections of ordered pairs, all set operations are applicable to them.
2. The resulting sets contain ordered pairs and are, therefore, relations.
3. If R and S denote two relations, then R റ S, known as intersection of R and S, defines a relation such that
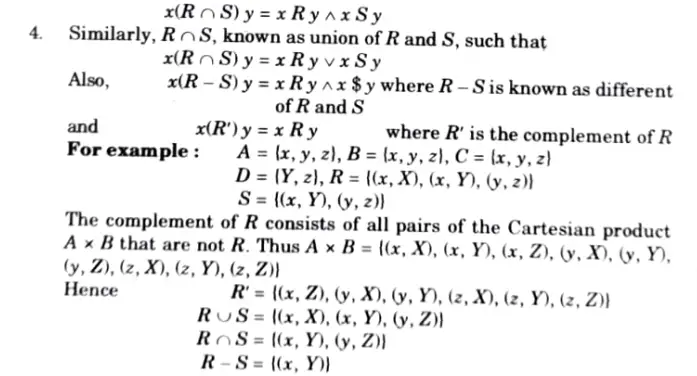
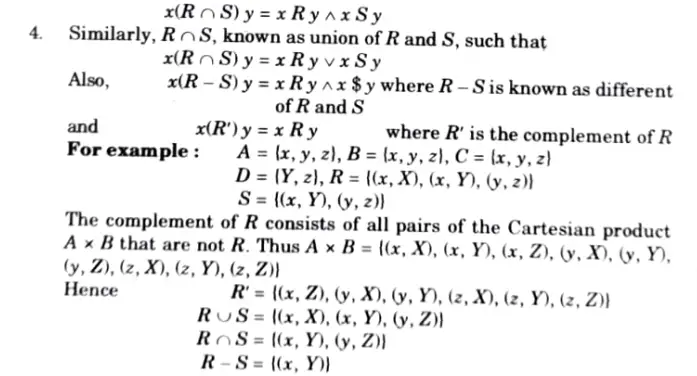
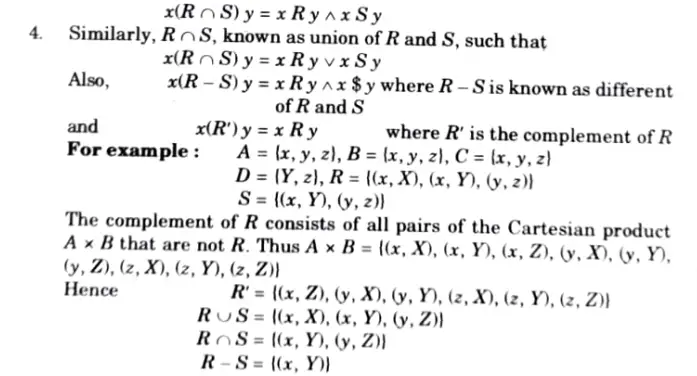
Q5. Show that R = {(a, b)|a ≡ b (mod m)) is an equivalence relation on Z. Show that if x1 ≡ y1 and x2 ≡ y2 then (x1 + x2) ≡ (y1 + y2).
Ans.



Q6. Let A(1,2, 3,…………., 13). Consider the equivalence relation on A xA defined by (a, b) R (c, d) if a + d = b+c. Find equivalence AKTU 2014-15, Marks 05 classes of (5, 8).
Ans.
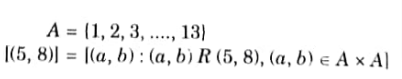
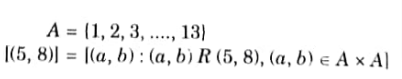
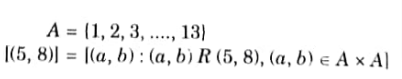
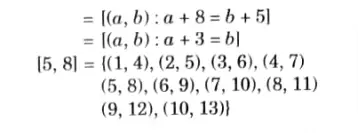
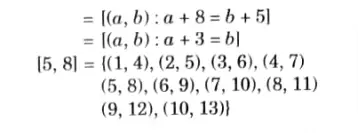
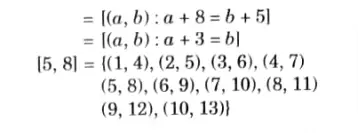



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Discrete Structures and Theory of Logics Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Discrete Structures and Theory of Logics Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |

4 thoughts on “Unit 01 SETS, FUNCTIONS & NATURAL NUMBERS in Discrete Structures Btech AKTU”