The Arithmetic and Logic Unit (ALU) is covered in Unit 02 of Computer Organization and Architecture. It is the CPU’s core component that performs arithmetic and logic tasks. This unit covers Boolean algebra, half and full adders, binary adders, subtractors, comparators, and multipliers.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Computer Organization and Architecture: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. Describe sequential Arithmetic and Logic Unit (ALU) using proper diagram.
Ans.
- 1. With the aid of a multiplexer, we may combine arithmetic and logic circuits to create arithmetic and logic units.
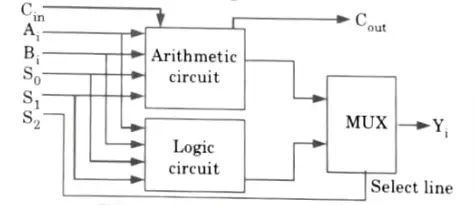


- 2. When the mode select line S2 =0, this ALU acts as an arithmetic circuit so the output of arithmetic circuit is transferred as final output.
- 3. Otherwise (S2 = 1) the output of the logic circuit is transferred as final output.
- 4. Based on the mode select S2 and input carry Cin. we increase or decrease the number of arithmetic and logic operations.
- 5. When S2 = 0, the ALU performs arithmetic operation and when S2 =1, with Cin = 0, the ALU performs logic operations.
- 6. We know that the carry input is not required in the logie circuits.
- 7. When logic operation is selected (S2 = 1), the carry input must be zero.
- 8. This given us the output sum in full adder circuit as



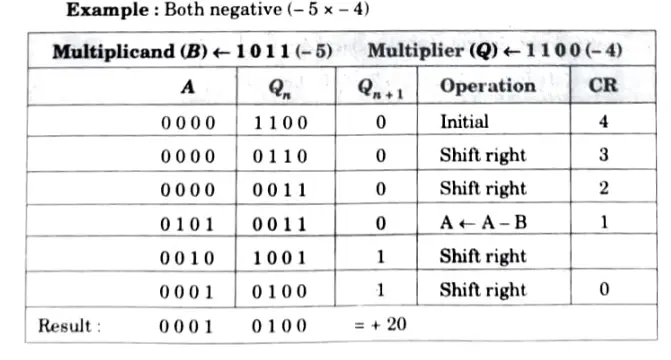
Q2. Explain Booth’s multiplication algorithm in detail.
Ans. The algorithm for 2’s complement multiplication is as follows:
Step 1: Load multiplicand in B, multiplier in Q. For negative numbers, 2’s complement format to be used.
Step 2 : Initialize the down counter CR by the number of bits involved.








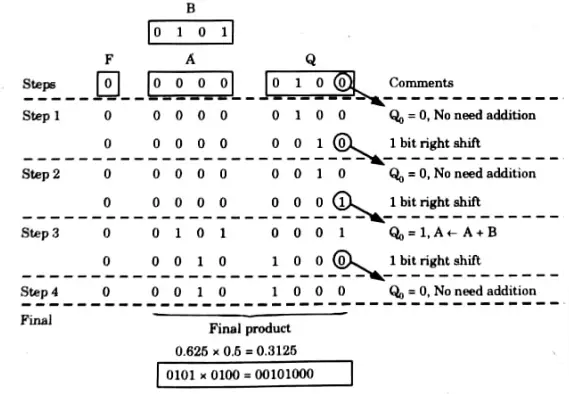
Q3. Give the Robertson multiplication algorithm for 2’s compliment fractions. Also illustrate the algorithm for 2’s compliment fraction by a suitable example.
Ans. Robertson algorithm:
1. A ← 0,B ← Multiplicand Q ← Multiplier and count ←n.
2. If Qo = 1 then perform A ← A+ B.
3.Shift right register F.A.Q by 1 bit F ← B [n – 1] AND Q [0] OR F and count ← count- 1.
4. If count > 1 Repeat steps 2 and 3, otherwise if Qo = 1 then perform A ← A-B and set Q [0] = 0.
For example: We perform the multiplication of fraction as:
Multiplicand = 0.625
Multiplier = 0.5
Equivalent binary representation 0.625 = 0101
2’s complement representation-0.625 = 1010 + 1(-0.625) = 1011
Equivalent binary representation +0.5 = 0100
2 complement representation – 0.5 = 1011 + 1-0.5 = 1100


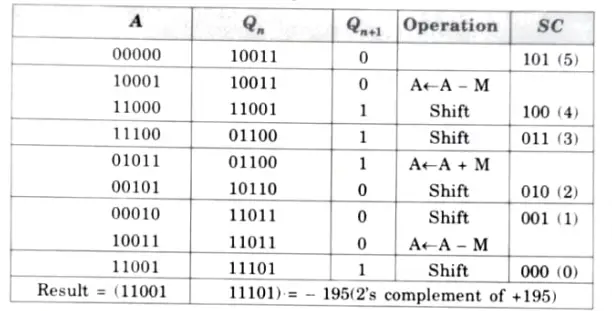
Q4. Show step by step the multiplication process using Booth’s algorithm when (+ 15) and (- 13) numbers are multiplied. Assume 5-bit registers that hold signed numbers.
Ans. 15 01111
– 13 = 2’s complement of 13 = 10011
Multiplicand (M) = 01111, Multiplier = 10011


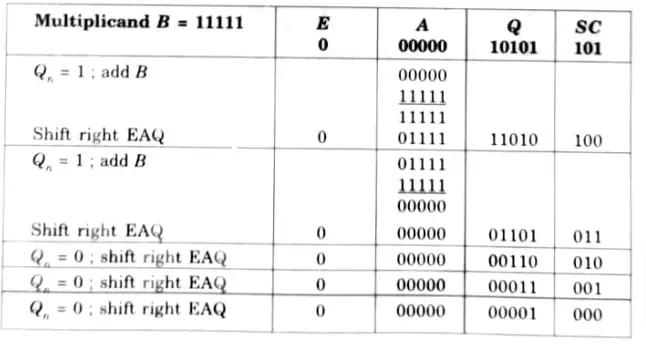
Q5. Show the contents of the registers E, A, Q, SC during the process of multiplication of two binary numbers 11111 (multiplicand) 10101 (multiplier). The signs are not included.
Ans.


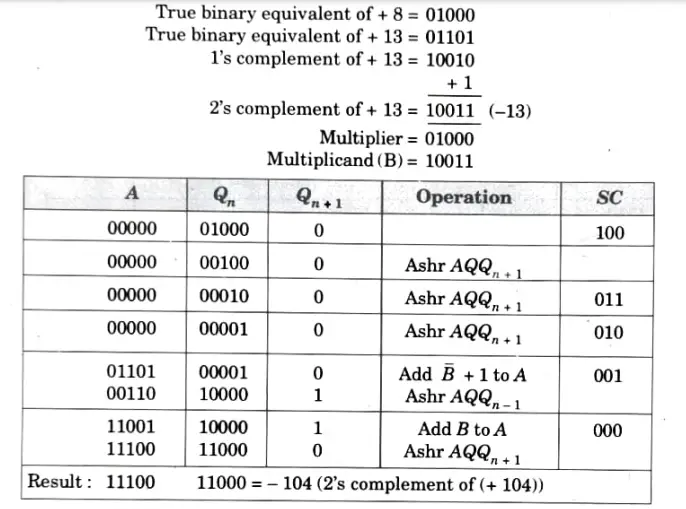
Q6. Show the multiplication process using Booth’s algorithm when the following numbers are multiplied: (-13) by (+8)
Ans.





Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Computer Organization and Architecture Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Computer Organization and Architecture Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |

1 thought on “Unit 02 Arithmetic and Logic Unit in Computer Organization and Architecture”