Achieve B.Tech success with Aktu’s Quantum Notes. Discover the world of Computer Graphics by reading these important notes that include important and recurrent questions. Exam excellence made simple! Unit-3 Three Dimensional
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Computer Graphics: *Quantum *B.tech-Syllabus *Circulars *B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. What do you mean by geometric primitives ? Discuss.
Ans. The fundamental geometrical shapes that go into creating computer graphics scenes and the finished visuals are known as geometric primitives.
Commonly used 3D geometric primitives include:
- 1. Points: A point is an exact position or location on a plane surface.
- 2 Line: Lines are employed to represent linear objects with insignificant width and height when geometry is used to model the real world.
- 3. Line segments: A line segment is a section of a line that has two end points and includes all of the points on the line in between them.
- 4. Planes: A plane is the two dimensional analogue of a point (zero dimensions), a line (one-dimension) and a space (three-dimensions).
- 5. Circles: A circle is a straightforward shape in Euclidean geometry made up of points on a plane that are equally spaced apart from a central point.
- 6. Ellipses: Ellipses, which emerge from the intersection of a circular cone with a plane that does not pass through its apex, are closed curves and the bounded case of conic sections.
- 7. Triangles: A triangle is a polygon with three line-segmented corners, or vertices, and three sides, or edges.
- 8. Polygons: Traditionally, a polygon is a plane figure with a closed path or circuit that is made up of a finite number of straight line segments.
- 9. Spline: A spline is a unique function that is better than polynomial interpolation and is defined piecewise by polynomials.
- 10. Spheres: A sphere, which has the form of a round ball, is a fully spherical geometrical object in three dimensions.
Q2. Write the steps involved in constructing 3D viewing transformation.
Ans. The steps involved in constructing 3D viewing transformations:
The complete three dimensional viewing process (without hidden surface removal) is described by the following steps:
- 1. Transform coordinates from world coordinates to normalized viewing coordinates by applying the transformation Npar Or Nper.
- 2. Clip in normalized viewing coordinates against the canonical clipping volumes.
- 3. Project onto the screen projection plane using the projections Par or Per.
- 4. Apply the appropriate (two dimensional) viewing transformation.
In terms of transformations, we can describe the above process in terms of a viewing transformation VT where
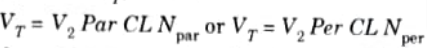
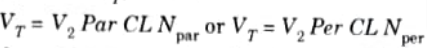
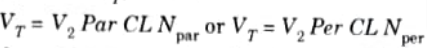
Here CL and V2 refer to the appropriate clipping operations and two dimensional viewing transformations.
Q3. What do you mean by projection ? Differentiate between parallel projection and perspective projection.
Ans. Projection:
- 1. A projection is a two-dimensional representation of a three-dimensional item or scene; it is the shadow of the object.
- 2. Projections convert coordinate system points of dimension ‘n’ into coordinate system points of dimension ‘n’ less.
Types of projections :
- 1. Parallel projection:
- a. Parallel lines are used to translate coordinate points to the view plane in a parallel projection.
- b. These are linear transforms that can be used to create scale drawings of three-dimensional objects for use in blueprints.
- 2 Perspective projection:
- a. A perspective projection transforms the locations of objects to the view plane via lines that converge at the centre of the projection.
- b. Calculating the point at which the projection lines and the view plane intersect provide the projected view of an object.
Difference:
| S. No. | Parallel projection | Perspective projection |
| 1. | When an object is projected in parallel, parallel lines are drawn from each of its vertices all the way to the view plane. | Perspective projection produces realistic view. |
| 2. | Lines of projection are parallel. | Lines of projection are not parallel. |
| 3. | These are linear transform. | These are non-linear transform. |
| 4. | In parallel projection, the center of projection is at infinity | In perspective projections, the center of projection is at a point. |
Q4. Explain the matrix for perspective projection for three vanishing points.
Ans. Matrix for perspective projection for three vanishing point :
- 1. A three vanishing point projection occurs when the three principal axes cross the projection plane, meaning that none of the axes is perpendicular to the projection plane.
- 2. To recreate the outline of a 3D object, three vanishing point perspective transformations are required.
- 3. The matrix representation of three vanishing point perspective transformation is
- 4. It has three center of projections, one on x-axis at [-1/p, 0,0,1], second on y-axis at [0, – 1/q, 0, 1] and third on z-axis at [0,0,-1/r,1].
- 5. It also has three vanishing points, one on X-axis [1/p, 0, 0, 1], one on y-axis at [0, 1/q, 0, 1] and third on z-axis at [0, 0, 1/r, 1|.
Q5. What do you mean by 3D clipping ? Discuss in detail.
Ans.
- 1. Extending techniques for two-dimensional clipping can be used to create three-dimensional clipping.
- 2. With 3D clipping, the objects are clipped against the view volume’s boundary planes.
- 3. We would need to test the relative location of the line using the boundary plane equations for the view volume in order to clip a line segment against it.
- 4. By modifying the plane equation of each boundary to include the line endpoint coordinates, which establishes whether the endpoint is inside or outside that boundary.
- a. An endpoint (x, y, z) of a line segment is outside a boundary plane if Ax + By + Cz + D > 0
- b. Similarly, the point is inside the boundary if Ax + By + Cz +D < 0.
- c. Lines with both endpoints outside a boundary plane are discarded, and those with both endpoints inside all boundary planes are saved.
- 5. The intersection of a line with a boundary is found using the line equations along with the plane equation.
- 6. Intersection coordinates (x1, y1, z1) are values that are on the line and that satisfy the plane equation Ax1+ By1 + Cz1 +D = 0, where A, B, C, and D are the plane parameters for that boundary.
Q6. Find the transformation for (a) cavalier with 𝛳 = 45° and (b) cabinet projection with 𝛳 = 30°.
Ans. a. A cavalier projection is an oblique projection where there is no foreshortening of line perpendicular to the xy plane. We then see for f = 1, with 𝛳 = 45°, we have
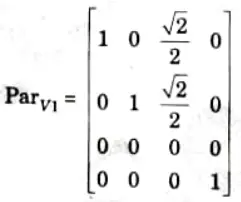
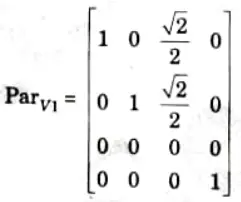
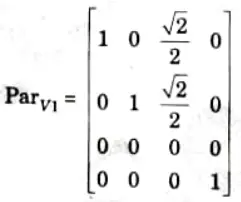






Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Computer Graphics Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Computer Graphics Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
