With Aktu’s Quantum Notes, you can unlock your success in B.Tech. Explore the world of Computer Graphics with these vital notes that include frequently asked questions. Exam success is now simple! Unit-2 Transformation
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Computer Graphics: *Quantum *B.tech-Syllabus *Circulars *B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. What do you understand by homogeneous coordinate ?
Ans. 1. The definition of homogeneous coordinates states that they are the coordinates that multiply all of the geometric transformation equations.
2. Coordinates are represented with three element column vectors, and transformation operations are written as 3 x 3 matrices. For translation we have:
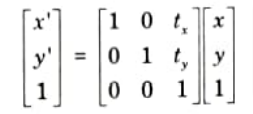
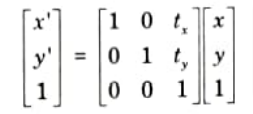
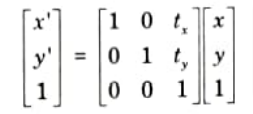
Which we can write in the abbreviated form as:
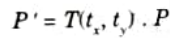
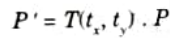
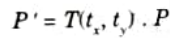
3. The inverse of translation matrix is obtained by replacing the translation parameters tx, and ty with their negatives i.e., -tx and -ty.
4. Rotation transformation equations about the coordinate origin are now written as:
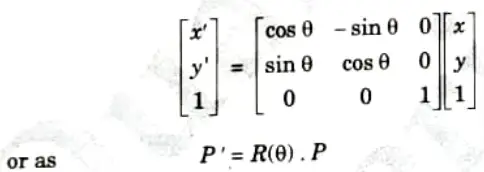
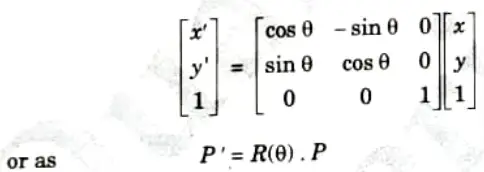
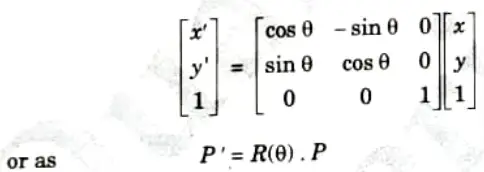
We get the inverse of rotation matrix when 𝛳 is replaced with – 𝛳.
5. Finally a scaling transformation relative to the coordinate origin is now expressed as matrix multiplication.
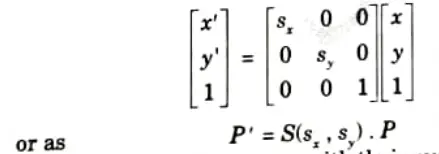
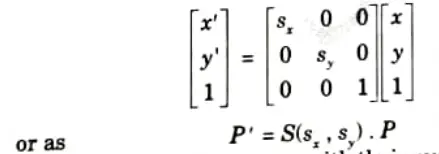
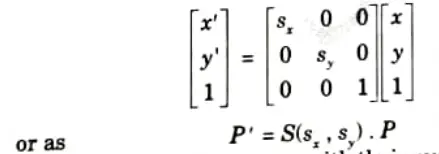
Replacing these parameters with their multiplicative inverse (1/sx and 1/sy) yields the inverse scaling matrix.
Q2. Write a procedure for rotation. Derive reflection metrics for reflection about X-axis.
Ans. Procedure for rotation: Rotation can be done in the following order
Step 1: Translate the object or body at the origin (translation).
Step 2: Rotate by any angle as given (rotation).
Step 3: Translate back to its original location (inverse translation).
In matrix form, it can be shown as
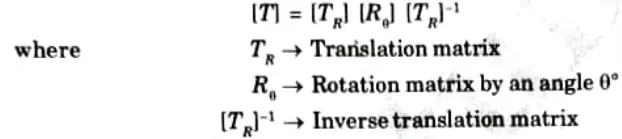
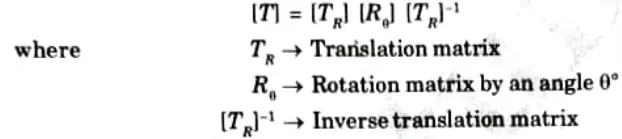
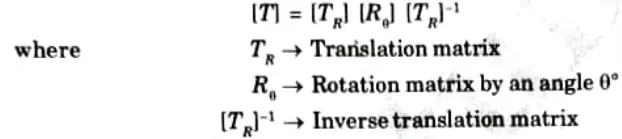
Reflection metrics: For reflection about x-axis, x coordinate is not changed and sign of y coordinate is changed. Thus if we reflect point (a, y) in the x-axis, we get (x, -y)



So, the transformation matrix for reflection about x-axis or y=0 axis is,
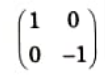
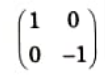
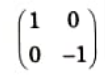
and the transformation is represented as
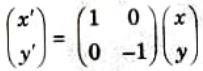
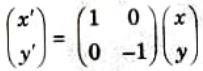
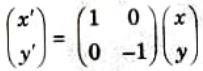
Q3. Show that the reflection about the line y = -x is equivalent to a reflection relative to the y-axis followed by an anticlockwise rotation of 90°.
Ans. Reflection matrix about the line y = -x






Reflection then rotation composite matrix is
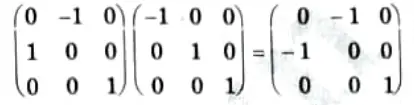
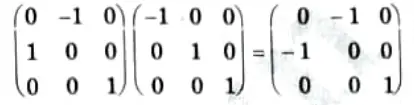
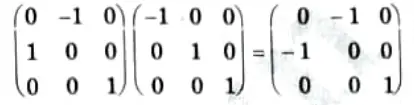
which is equal to the transformation matrix for reflection about the line y = -x.
Q4. What do you understand by the term “Clipping and Windowing” ?
Ans. Clipping:
- 1. The process of identifying the parts of a picture that are either inside or outside of a particular region of space is called clipping.
- 2. You can clip a point, line, area, or piece of text.
- 3. The clipping window is the area against which an object is to be clipped.
Windowing:
- 1. The practise of choosing and viewing a photograph from various angles is known as windowing.
- 2. A viewport is the portion of a display device to which a window is assigned.
- 3. In the typical position, a window and viewports are rectangles with their edges parallel to the coordinate axes.
Ans. Window to view point coordinate transformation: Window to viewport mapping or transformation is done in following three steps:
Step 1: When the window’s lower left corner reaches the origin, the object and its window are also translated.
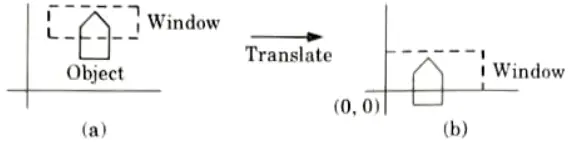


Step 2: The object and window are then scaled until the window and viewport have identical dimensions. In other words, the item is being transformed into an image and a window for the viewport.
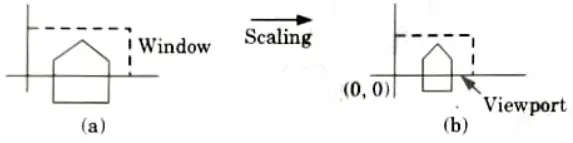


Step 3: Another translation is used as the last transformation step to reposition the viewport on the screen where it should be.
Issues related to multiple windowing:
- 1. A key problem in multi-windowing is how to automatically assign windows to the relevant areas within an image.
- 2. More difficult to work with several applications at once.
Q6. What is polygon mesh ? Discuss various ways to represent a polygon mesh with their merits and demerits.
Ans. Polygon mesh:
- 1. A polygon mesh is a 3D object’s collection of vertices, edges, and faces.
- 2. Whether they are utilized for 3D animated films, advertisements, or video games, every 3D character and item has a polygon mesh that specifies their shape and contour.
- 3. The x, y, and z coordinates are stored at each vertex of the polygon mesh.
- 4. The rendering engine uses surface information from each face of that polygon to generate lighting and shadows (among other things).
Representation of a polygon mesh: Polygon meshes may be represented in a variety of ways, using different methods to store the vertex, edge and face data. These include :
1. Vertex-vertex meshes: Only vertices that point to other vertices are represented by a vertex-vertex mesh. In the representation, the edge and face information are both implicit.
Merits: Vertex-vertex meshes benefit from small storage space and efficient morphing of shape.
Demerits: Due to the representation’s simplicity, meshes cannot be subjected to many effective operations.
2. Face-vertex meshes: A set of faces and a set of vertices are used to represent an object in pace-vertex meshes. As the input that most modern graphics hardware accepts, this is the mesh representation that is utilised the most frequently.
Merits: Explicit lookup of a face’s vertices and the faces that surround a vertex is possible with face-vertex meshes.
Demerits: Using face-vertex meshes, it is challenging to do dynamic operations like splitting or merging a face.
3. Winged-edge meshes:Each edge in a winged-edge mesh points to two vertices, two faces, and the four edges (clockwise and anticlockwise) that touch those points. Winged-edge meshes provide continuous time surface navigation.
Merits: Split and merge operations in winged-edge meshes can be completed quickly. The mesh geometry can be changed dynamically thanks to this, which offers significant flexibility.
Demerits: The main disadvantages are the high storage needs and heightened complexity brought on by the need to maintain numerous indexes.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Computer Graphics Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Computer Graphics Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
