Utilise Quantum Notes to improve your preparation for Strength of Materials. Find important questions that appear regularly in Aktu Btech exams. Get the advantage you require to succeed! Unit-3 Springs, Columns and Struts
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Strength of Material: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. A closed-coiled helical spring having 24 turns is made of 8 mm diameter wire. The mean diameter of the spring is 80 mm and it carries a load of 250 N. Determine the shear stress developed, the deflection and the stiffness of the spring. Take G = 84 GPa.
Ans. Given: Diameter of wire, d = 8 mm, Number of turns, n = 24, Mean
diameter of coil, D = 80 mm, Radius of coil, R = D/2= 80/2 = 40 mm,
Axial load, W = 250 N, Modulus of rigidity, G=84 GPa or 8.4 x 104 N/mm2
To Find: i. Shear stress developed.
ii. Deflection of the spring
iii. Stiffness of the spring
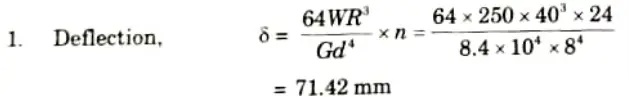
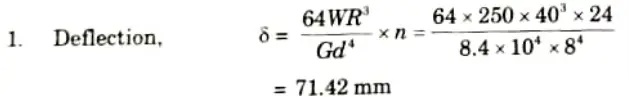
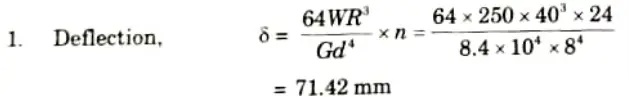
2. Stiffness of the spring,
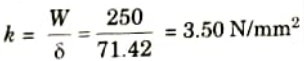
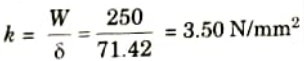
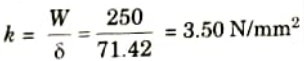
3. Maximum shear stress,
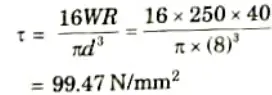
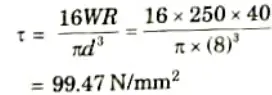
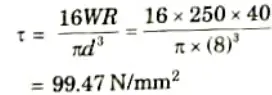
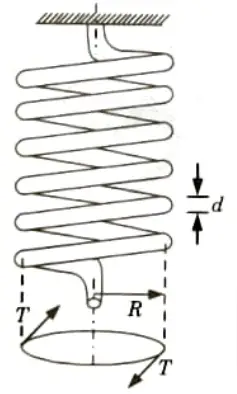
Q2. Find the expression for energy stored in closed coiled helical spring subjected to an axial torque.
Ans.
- 1. The axial torque T tends to wind up the spring by producing approximately a pure bending moment at all cross-sections (Fig.).
- 2. When bending moment is applied to curved bars with small curvature (T is the applied bending moment),
Where R and R’ are the radii of curvature before and after applying the bending moment.
- 3. Let n and n’ be the number of turns of the spring before and after applying the bending moment.
Then length of spring, l = 2𝝅nk = 2rn’R’ or n’ = n(R/R’)
- 4. If 𝝓 is the angle of rotation of one end of the spring relative to the other and about the axis,





5. Then strain energy due to torsional effect,
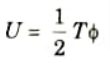
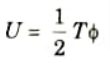
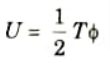
Q3. Explain middle quarter rule for circular sections.
Ans. 1. Consider a circular section of diameter d’ as shown in Fig.
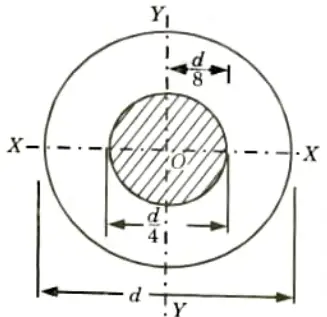


- 2. Let this section is subjected to a load which is eccentric to the axis Y-Y.
- 3. Let, P = E centric load, e = Eccentricity of the load



- 7. Now minimum stress is given by,



- 9. The above result shows that the eccentricity ‘e’ must be lesser than or equal to d/8.
- 10. It means that the load can be eccentric, on any side of the centre of the circle, by an amount equal to d/8.
- 11. Thus, if the line of action of the load is within a circle of diameter equal to one-fourth of the main circle as shown in Fig. then the stress will be compressive throughout the circular section.
Q4. Write the assumptions made in the Euler’s column theory. And also write different types of end conditions for long columns.
Ans. A. Assumptions made in the Euler’s Column Theory:
- 1. The load is applied axially to a perfectly straight column at first.
- 2. The column’s cross-section is constant along its whole length.
- 3. The column material complies with Hooke’s law and is completely elastic, homogenous, and isotropic.
- 4. As compared to the bending stress, the direct stress is quite low.
- 5. The column will collapse on its own.
- 6. The column’s self-weight is insignificant.
B. End Conditions for Long Columns: The following four types of end conditions of the columns are important:
- 1. Both the ends of the column are hinged (or pinned).
- 2. One end is fixed and the other end is free.
- 3. Both the ends of the column are fixed.
- 4. One end is fixed and the other is pinned.
Q5. Derive the expression for the critical buckling load for a column having one end fixed and the other end free.
Ans. 1. Take Y-axis towards right for positive value of y.
2. Viewing from the left end, P provides a clockwise bending moment P(a -y) on the left portion and is thus positive then,
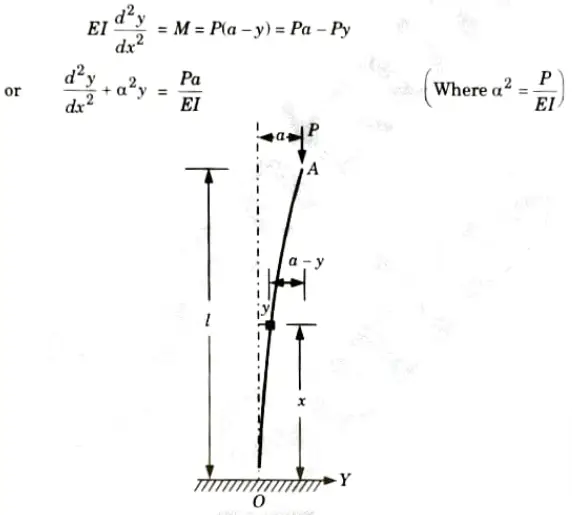


3. The solution is
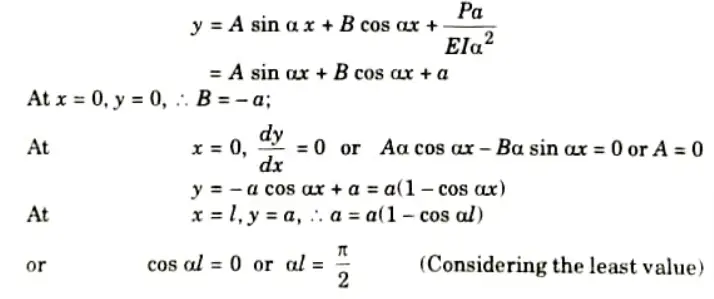
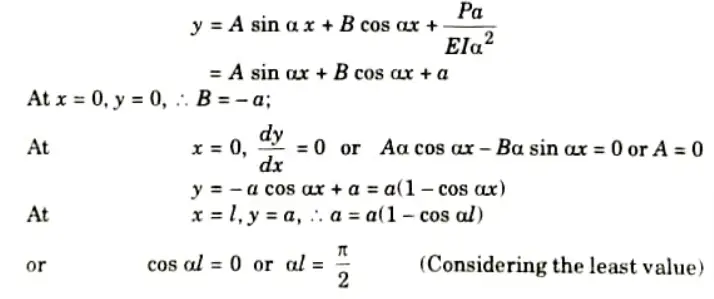
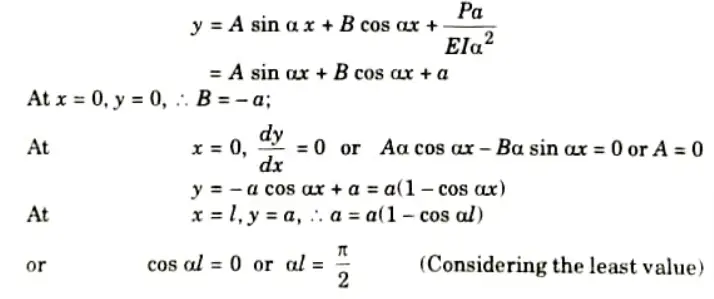



Q6. What are the limitations of Euler’s theory for buckling? Discuss Rankine-Gordon formula.
Ans. A. Limitations of Euler’s Theory for Buckling:
- 1. Euler’s formula is derived on the presumptions that the load is precisely axial and the struts are originally perfectly straight. But in reality, these presumptions are never true.
- 2. Initial curvature and some degree of eccentricity are always present. It should be noticed that Euler’s calculation does not include a strength attribute for the strut material.
- 3. E, which stands for the material’s stiffness properties, is the only property concerned.
- 4. As a result of these flaws, in real life struts deflect prior to the fatal load, and the deflection grows as the load increases. Because of this, the failure occurs due to stress rather than buckling and occurs before the Euler’s load is met.
B. Rankine-Gordon Formula:
- 1. Only very long, thin struts with very minor geometrical defects can be predicted to have buckling stresses using Euler’s formula.
- 2. Nevertheless, in actuality, the majority of struts experience plastic knockdown, and the experimentally reported buckling loads are significantly lower than the predictions of Euler.
- 3. For struts in this category, a suitable formula is the Rankine-Gordon formula which is a semi-empirical formula, and takes into account the crushing strength of the material, its Young’s modulus and its slenderness ratio, namely L/k



- 4. For a very short strut Pe is very large hence 1/Pe would be very small, so 1/Pe can be neglected.
- 5. Thus PR = Pc for very short strut and for very large struts, Pe is very small so 1/Pe would be large and 1/Pc can be neglected, hence PR = Pe.
- 6. The Rankine’s formula is therefore valid for extreme values of 1/k.
Thus, rewriting the formula in terms of stresses, we have
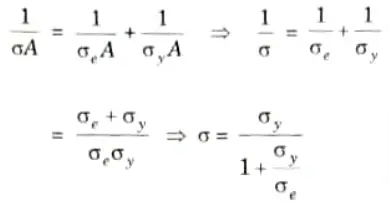
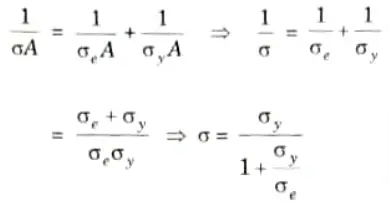
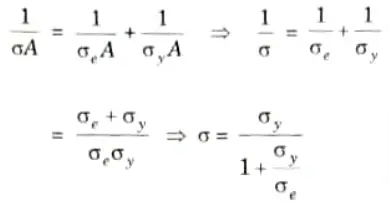
- 7. For struts with both ends pinned.
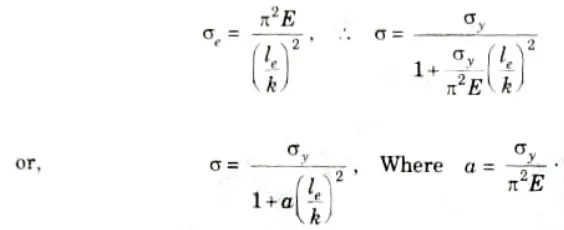
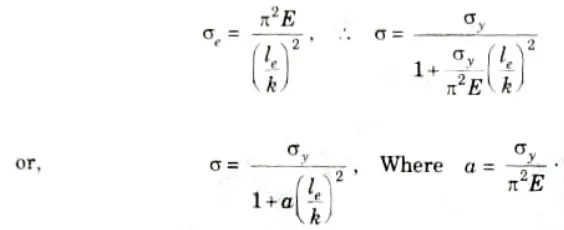
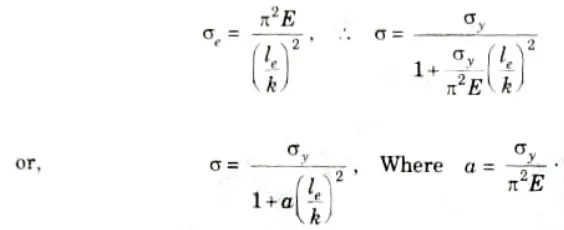



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Strength of Material Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Strength of Material Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One View) | Student Result |
