Quantum Notes will help you prepare for Strength of Materials. Discover the essential questions that appear regularly in Aktu Btech exams. Get the competitive edge you need! Unit-4 Cylinders and Spheres
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Strength of Material: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. A cylindrical shell is 3 m long, 1.5 m internal diameter and 20 mm metal thickness. Calculate the intensity of maximum shear stress induced and the change in dimensions of the shell and change in volume of the shell ifit is subjected to an internal pressure of 2 N/mm2. Take E = 2x 105 N/mm2 and 𝝁 = 0.3.
Ans. Given: Length of shell, L = 3 m= 300 cm, Internal diameter,
d = 1.5 m= 150 cm, Wall thickness, t = 20mm= 2 cm, Internal pressure,
P = 2 N/mm2, Young’s modulus, E = 2 x 105 N/mm2, Poisson’s ratio, 𝝁 = 0.3.
To Find: i. Intensity of maximum shear stress
ii. Change in dimensions and volume of the shell.
1. Maximum shear stress is given by,
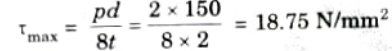
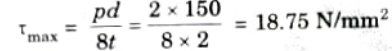
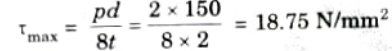
2. We know that,
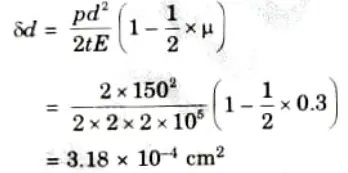
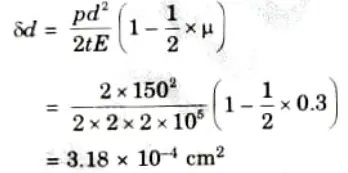
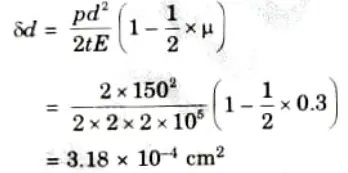
3. Change in length is given by.



4. We know that,



Q2. A spherical shell of 1.2 m internal diameter and 6 mm thickness is filled with water under pressure until its volume increases by 400 x 103 mm3. Find the pressure exerted by water on the shell. E = 200 GPa and 𝝁 = 0.3.
Ans. Given: d = 1.2 m = 1200 mm, t = 6 mm, 𝜟V = 400 x 103 mm3
E = 200 GPa = 2 x 10 N/mm2, 𝝁 = 0.3.
1. For spherical shell, volumetric strain is given as:



2. Original volume of shell,
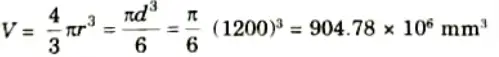
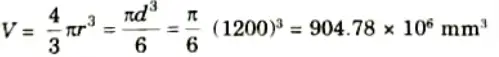
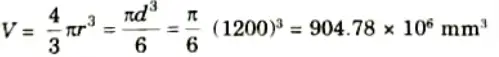
3. Now from eq. (4.8.1), we get
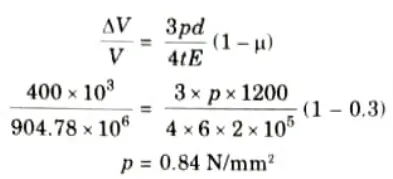
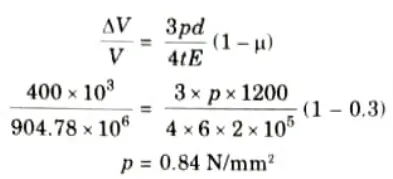
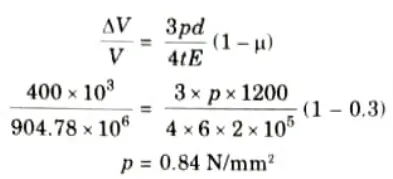
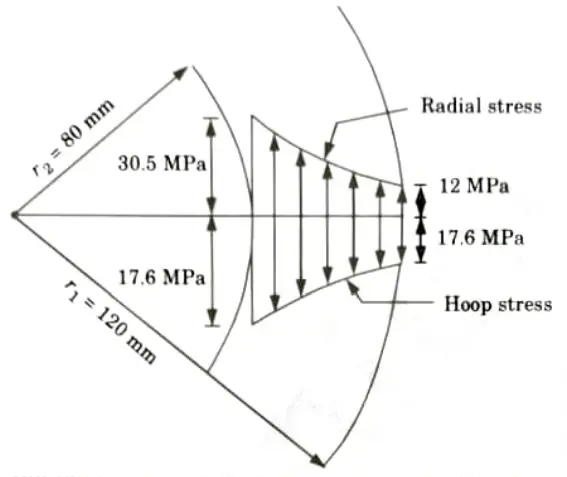
Q3. The maximum stress permitted in a thick cylinder, radii 8 em and 12 cm, is 20 N/mm2, the external pressure is 6 N/mm2, what internal pressure can be applied ? Plot curves showing the variation of hoop and radial stresses through the material.
Ans. Given: Internal radius, r2 = 8 cm = 80 mm, External radius, r1 = 12 cm = 120 mm, External pressure, p1 = 6 N/mm2
Maximum hoop stress, 𝝈x2 = 20 N/mm2
To Find: Internal pressure p2, hoop stress at outer face 𝝈x1
1. Hoop stress at inner face,
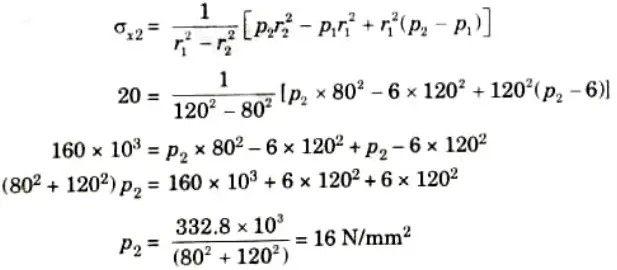
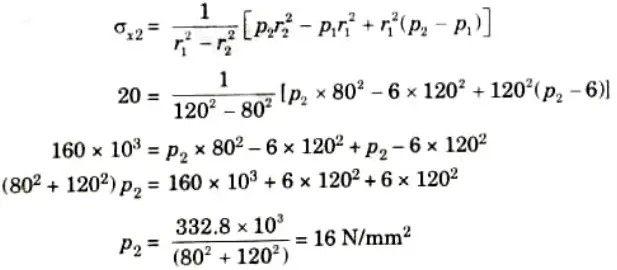
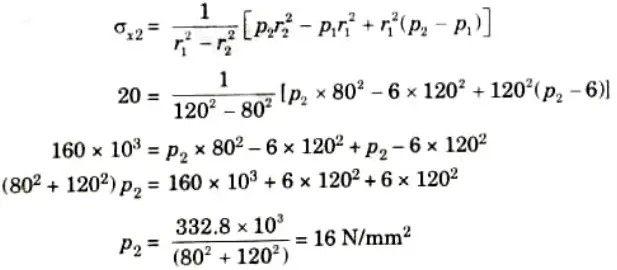
2. Hoop stress at outer face,
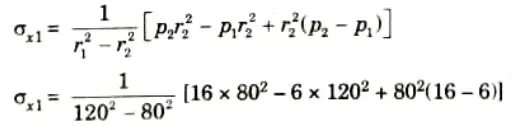
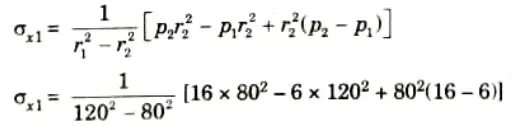
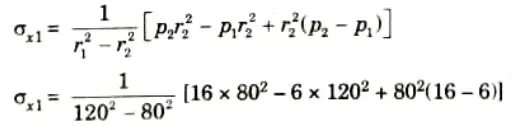
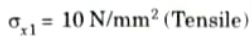
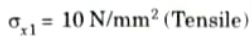
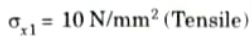
3. The variation of hoop and radial stresses through the material is shown in Fig.


Q4. The cylinder for a hydraulic press has an inside diameter of 300 mm. Determine the wall thickness required if the cylinder is to withstand an internal pressure of 60 MPa without exceeding a shearing stress of 90 MPa.
Ans. Given: d = 300 mm, p = 60 MPa, 𝝉max = 90 MPa
To Find: Wall thickness.
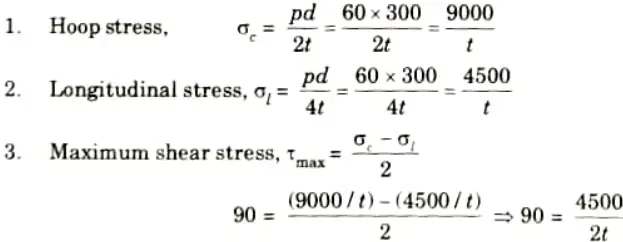
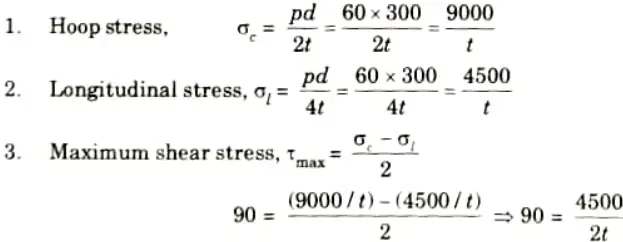
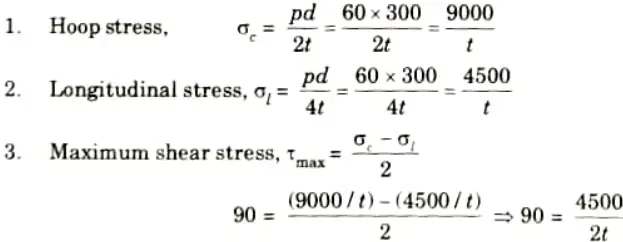
Thickness of wall, t = 25 mm
Q5. Derive the equations for circumferential stress and volumetric strain in a thin spherical shell under internal pressure.
Ans. A. Circumferential Stress:
- 1. Fig. shows a thin spherical shell of internal diameter d and thickness and subjected to an internal fluid pressure p.
- 2. The fluid inside the shell has a tendency to split the shell into two hemispheres along X-X axis.
- 3. The force (F) which has a tendency to split the shell
- 4. The area resisting this force = 𝝅dt
- 5. Hoop or circumferential stress (𝝈c) induced in the material of the shell is given by.
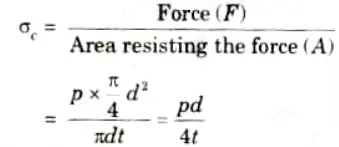
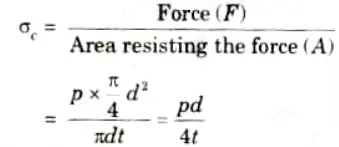
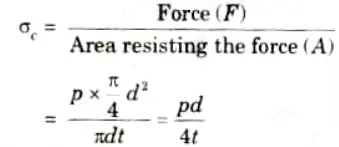
The stress 𝝈c is tensile in nature.
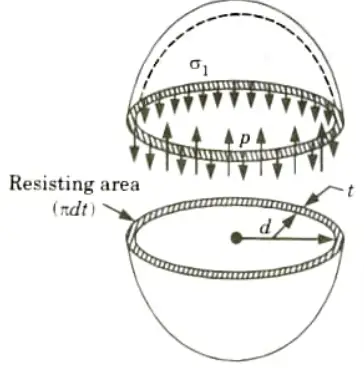


- 6. The fluid inside the shell is also having tendency to split the shell into two hemispheres along Y-Y axis. Then it can be shown that the tensile hoop stress will also be equal to pd/4t. Let this stress is 𝝈l.
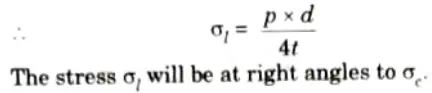
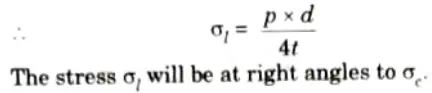
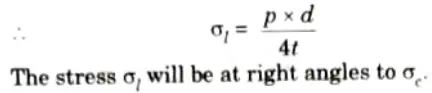
B. Volumetric Strain
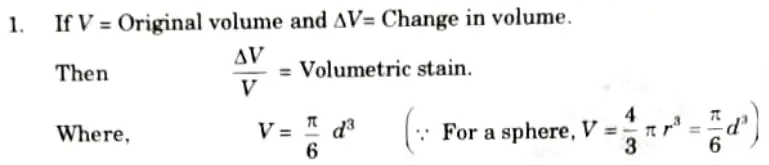
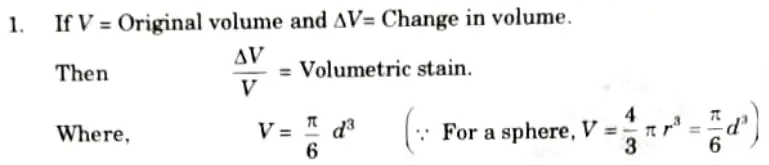
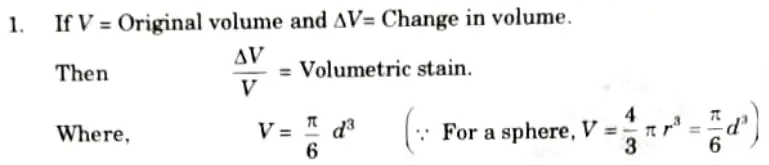
2. Taking the differential of the above equation,
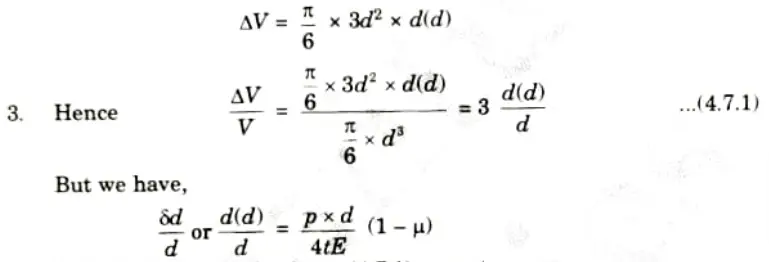
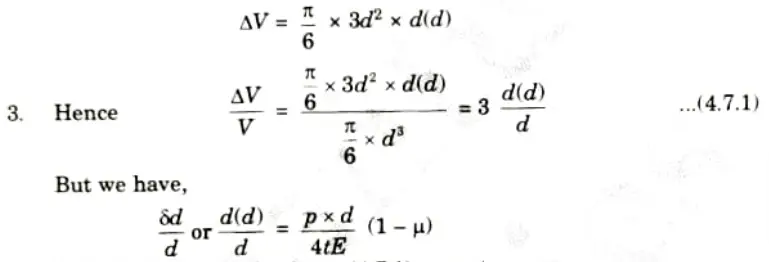
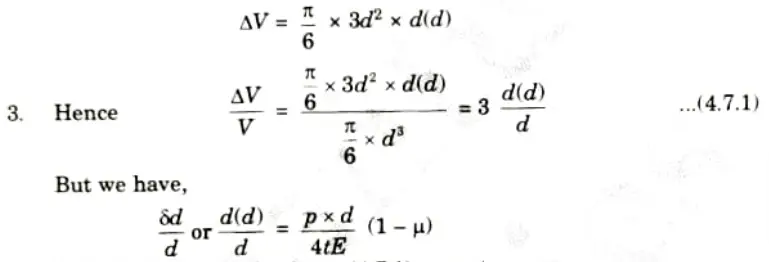
4. Substituting this value in eq. (4.7.1), we get
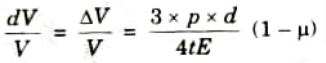
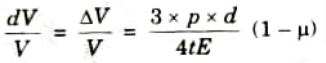
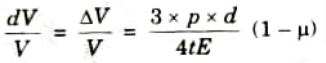
Q6. Discuss about the stresses induced in the compound thick cylindrical shells.
Ans. A. Stresses in Compound Thick Cylindrical Shells:
- 1. Both the inner and outer shells of the compound shell will experience hoop tensile stress when it is under internal pressure.
- 2. The resultant strains are more or less consistent as a result of both the initial stresses and those brought on by internal pressure.
- 3. Now consider a compound thick cylindrical shell made up of two tubes as shown in Fig.
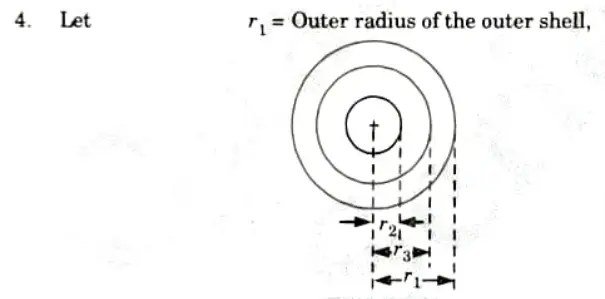





- 5. Now that the outside tube is exerting pressure on the inner shell, or in other words before the fluid under pressure is admitted into the inner shell, the Lame’s equations can be used with ease.
a. For Inner Tube:
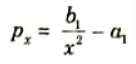
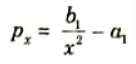
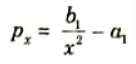
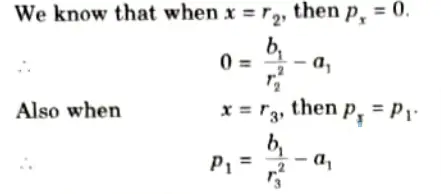
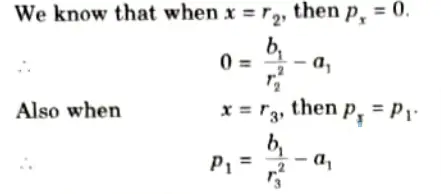
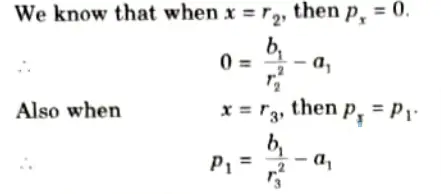
b. For Outer Tube:
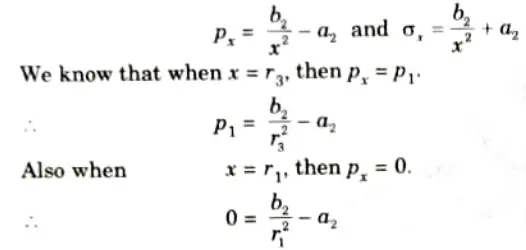
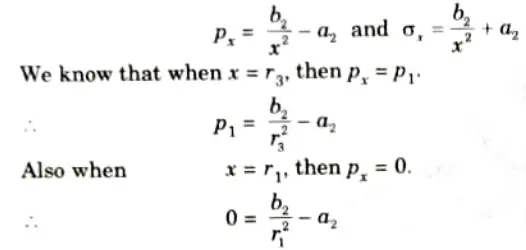
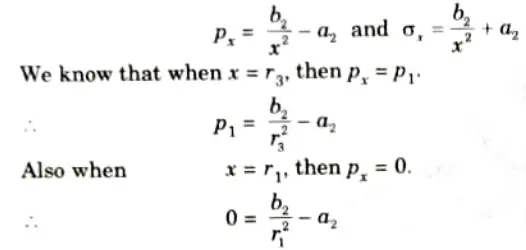
- 6. The values of a1, b1, a2, and b2, may be find out from the above four equations, if the radial pressure p1 at the junction of the two shells is known.
- 7. The hoop stress (𝝈x) may also be obtained with the help of relative expressions.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Strength of Material Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Strength of Material Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One View) | Student Result |
