Quantum Notes can help you prepare for Strength of Materials. Find crucial questions often asked in Aktu Btech exams. Get the competitive advantage you need! Unit-2 Beams and Torsion
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Strength of Material: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. A rectangular beam is to be cut out of a cylindrical log of wood with diameter d. Determine the ratio of depth to width of the strongest beam which can be had from log of wood.
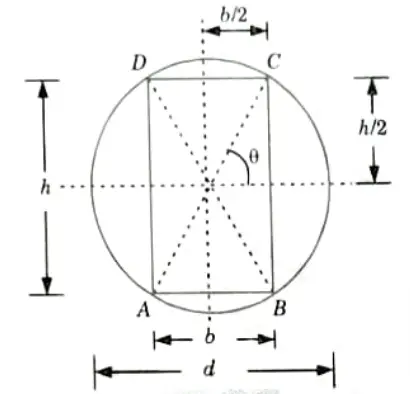


Ans. 1. Let ABCD be the strongest rectangular section which can be cut out of the cylindrical log.
2. Let, b = Width of section
h = Depth of section.
3. Now section modulus of the rectangular section is given as,
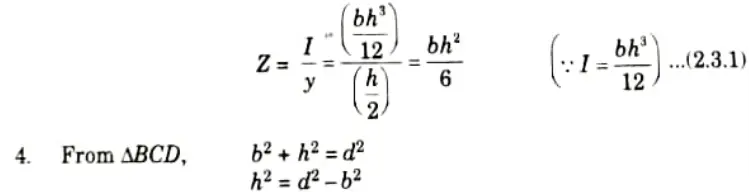
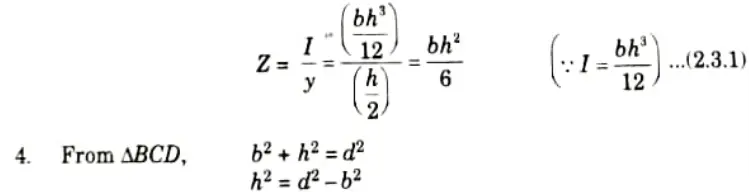
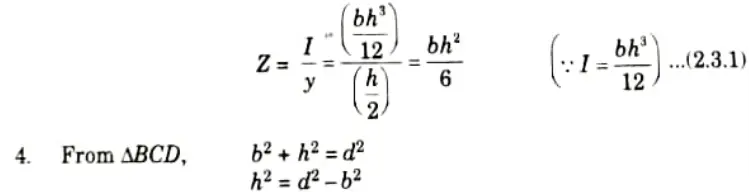
5. Substituting the value of h2 in eq. (2.3.1), we get
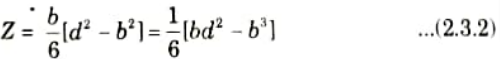
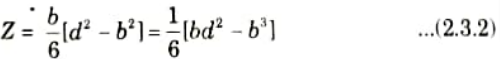
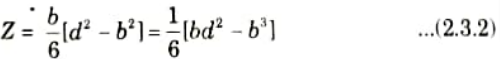
6. Now for the beam to be strongest, the section modulus should be maximum.
For maximum value of Z,
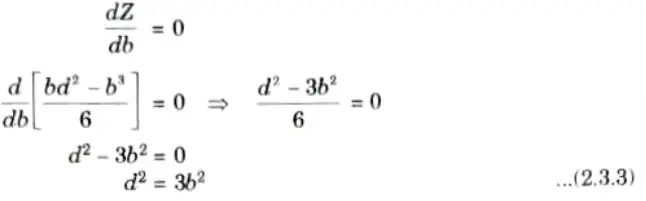
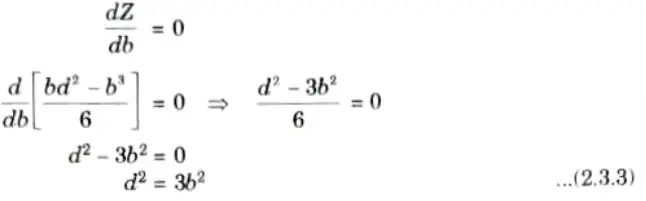
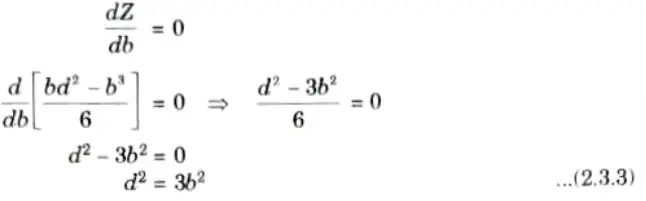
7. But from triangle BCD, we get



8. Substituting the value of d2 from eq. (2.3.4) in eq. (2.3.3), we get
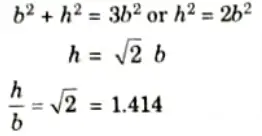
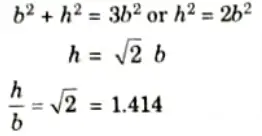
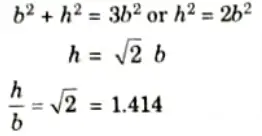
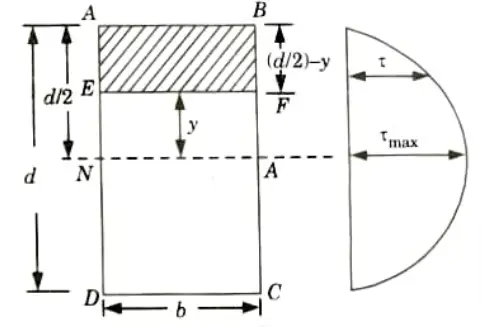
Q2. Show that for a rectangular section the maximum shear stress is 1.5 times the average stress.
Ans. 1. Let a rectangular section of width b and depth d is shown in Fig. and this section is subjected to shear force F. Consider a section EP at distance y from neutral axis.


2. Shear stress at this level is given by,



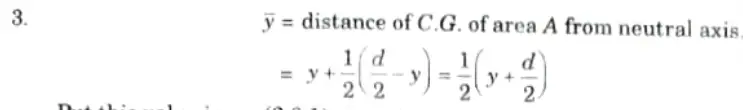
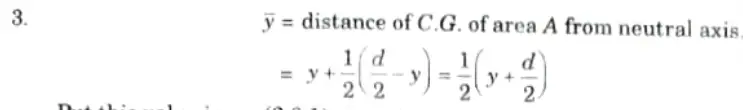
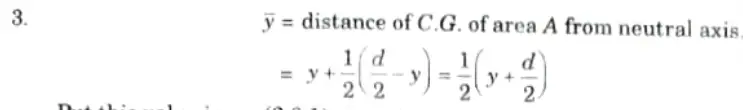
Put this value in eq. (2.8.1), we get
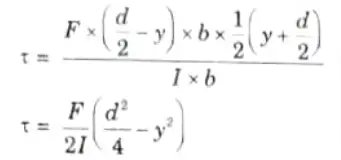
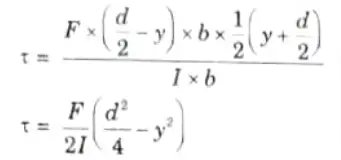
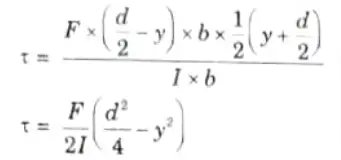
4. At the neutral axis shear stress is maximum.
Put y = 0 in above equation, we get
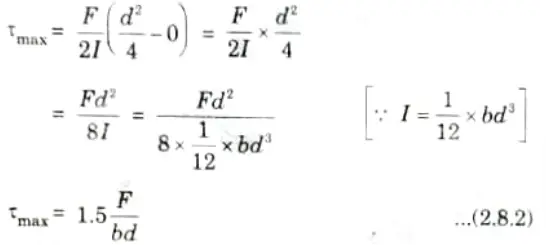
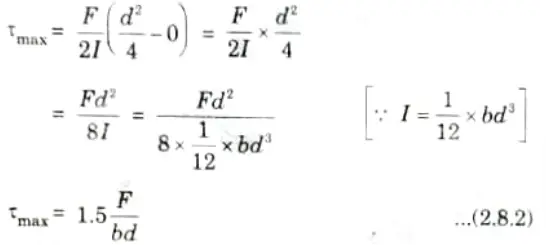
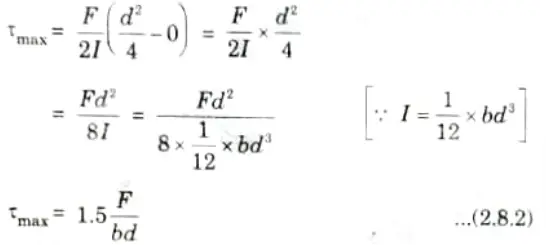
5. Average shear stress is given as,



6. From eq. (2.8.2) and eq. (2.8.3), we get
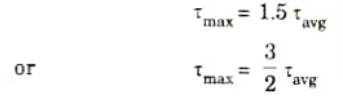
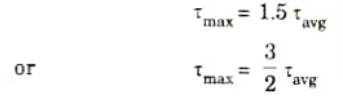
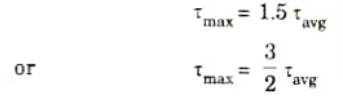
Q3. Derive an expression for the slope and deflection of a beam subjected to uniform bending moment.
Ans. 1. A beam AB of length L is subject to uniform bending moment M.
2. As shown in Fig. beam is subjected to a constant bending moment so it will bend into a circular arc.
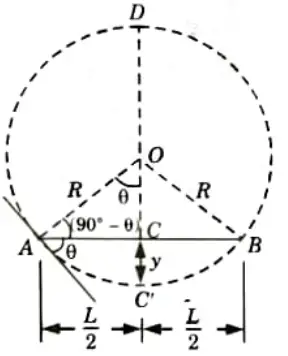


Here, R = Radius of curvature of the deflected beam,
Y = Deflection of beam at the center.
I = Moment of inertia of the beam,
E = Young’s modulus for beam material, and
𝜽 = Slope of the beam at the end.
3. Now, from the geometry of the circle
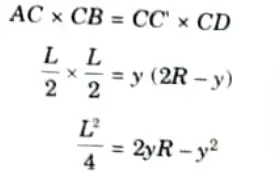
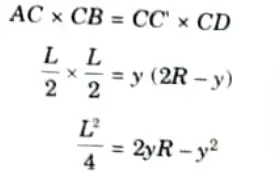
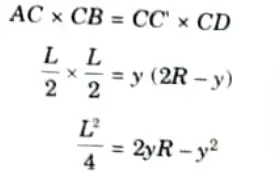
4. If deflection y is very small, then y2 is too small so we neglect it,
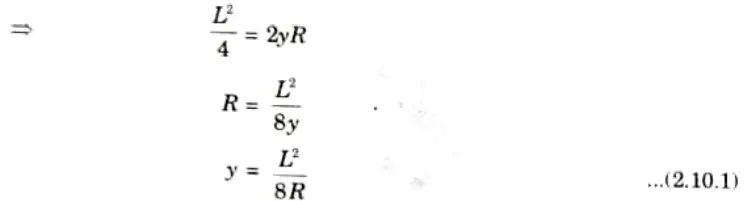
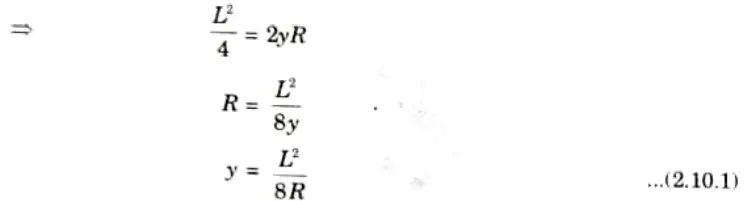
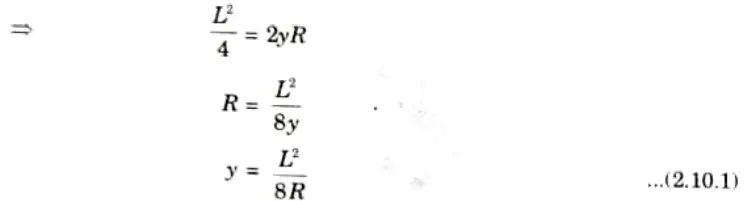
5. Now from bending equation, we get
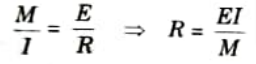
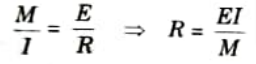
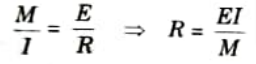
6. Put the value of R in eq. (2.10.1), we get
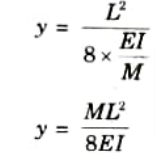
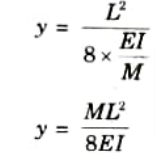
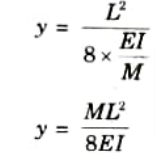
7. This equation gives the value of central deflection of beam.
Value of Slope:
1. From triangle AOC,
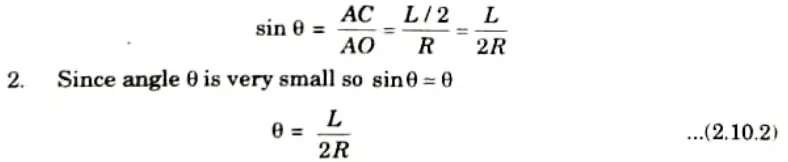
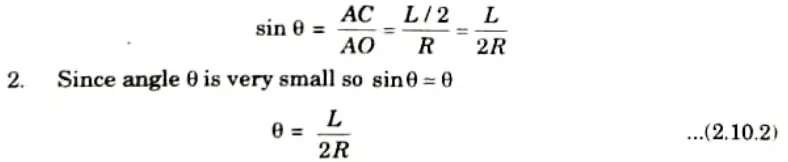
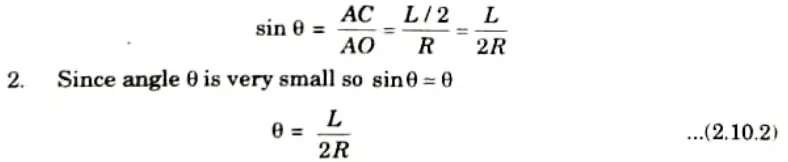
3. Put the value of R in eq. (2.10.2), we get
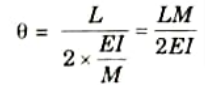
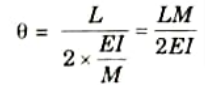
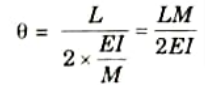
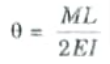
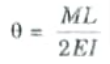
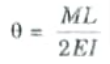
4. This is the value of slope of beam. Due to symmetry, slope at point A and B should be equal
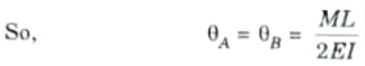
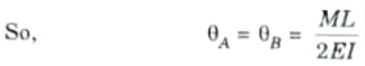
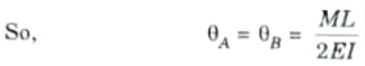
Q4. Establish the governing differential equation of beams. What are its limitations?
Ans. A. Derivation of Differential Equation of Deflection Curve:
1. Consider a small portion PQ of a beam, bent into an are as shown in Fig.
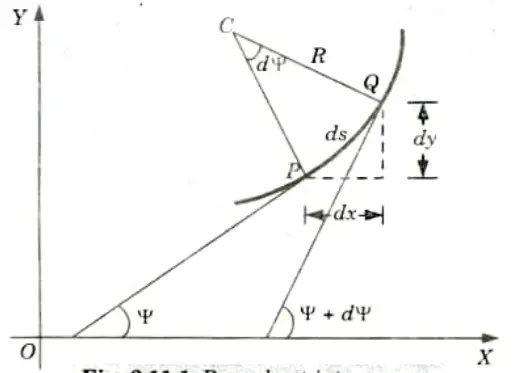





3. From the geometry of the figure, we find that



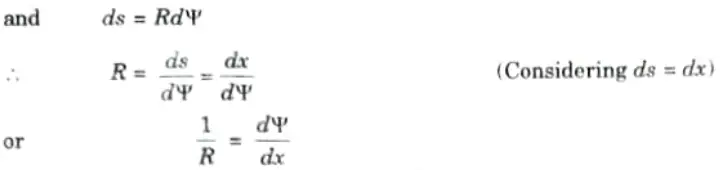
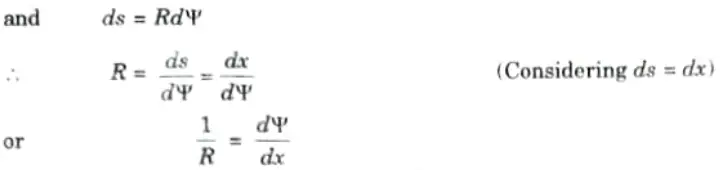
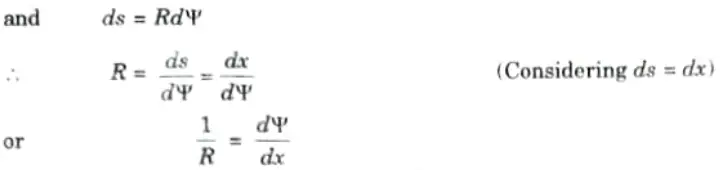
4. We know that if x and y be the coordinates of point P, then
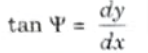
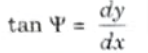
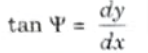
5. Since 𝜳 is a very small angle, therefore taking tan 𝜳 = 𝜳,



6. We also know that,
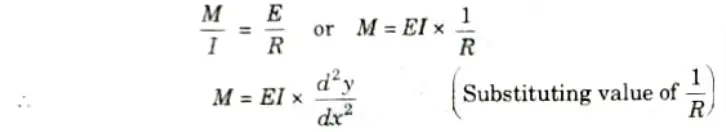
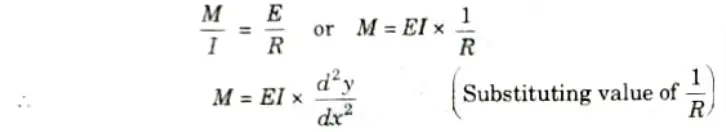
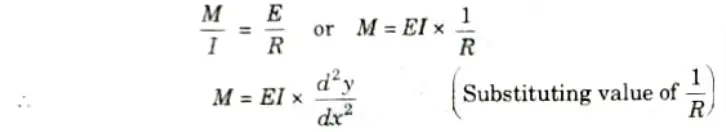
B. Limitations:
- 1. Not valid for the beams which do not obey Hook’s law.
- 2. Not applicable for the beams which have large curvature.
Q5. Compare the resistance to torsion of a hollow shaft to that of a solid shaft if the inside diameter of the hollow shaft is two third of the external diameter and the two shafts have the same material and weight and of equal length.
Ans. Given: dH = 2/3 DH
To Find: TH/TS
1. We know that,
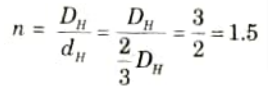
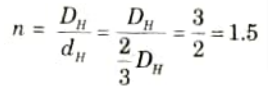
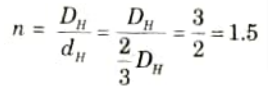
2. For same length, same material and same weight, the ratio of resistance to torsion is given as,
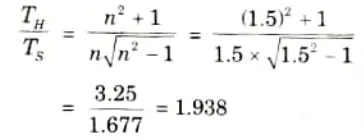
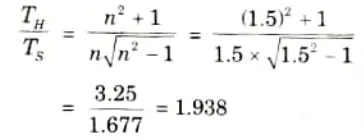
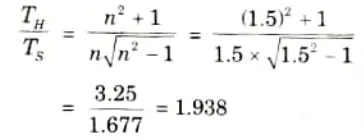
Q6. Determine the internal and external diameter of a hollow shaft whose internal diameter is 0.6 times external diameter and transmits 120 kW at 210 rpm and the allowable stress is limited to 75 MPa. If bending moment of 2800 N-m is applied to the shaft, find the speed at which the shaft must rotate to transmit the same power for the same value of maximum shear stress.
Ans. Given: Di = 0.6Do P= 120 kW, N= 210 rpm, 𝝉 = 75 MPa, M= 2800 N-m
To Find: i. Internal and external diameter of hollow shaft.
ii. Speed of shaft at applied bending moment.
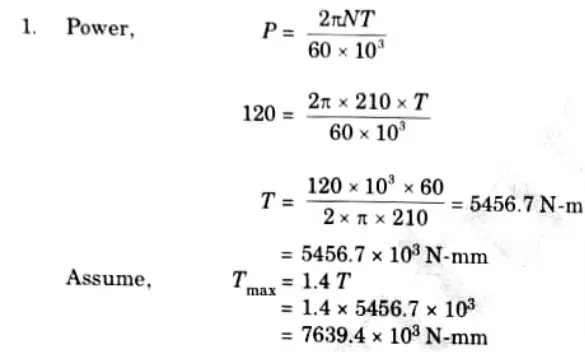
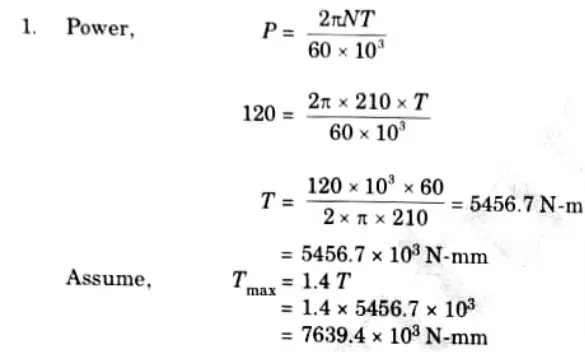
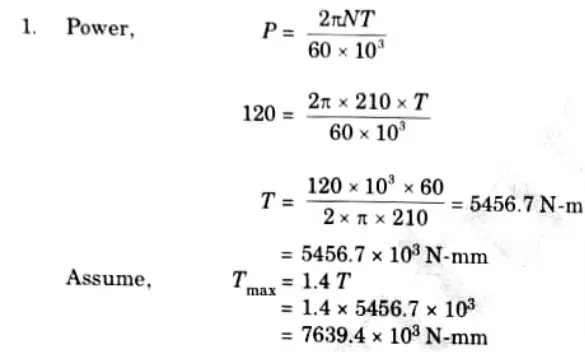



3. Maximum shear stress,
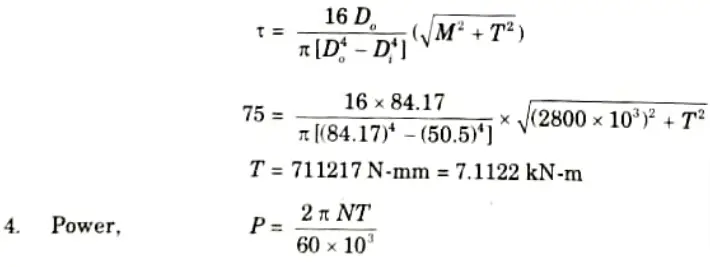
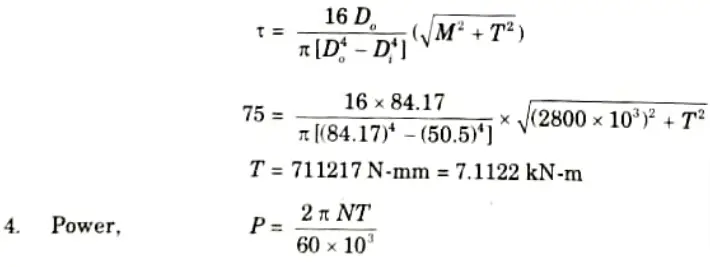
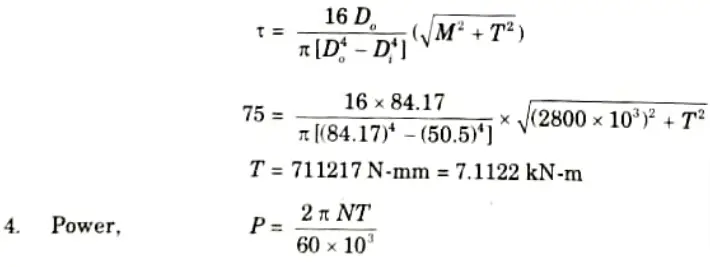
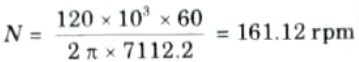
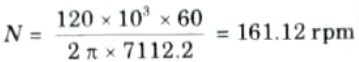
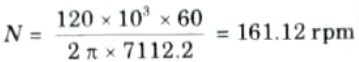



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Strength of Material Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Strength of Material Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One View) | Student Result |
