Discover B.Tech AKTU Quantum Book Short Question Notes on Strength of Material. Discover the fundamentals of structural mechanics, stress analysis, and material behaviour for reliable and secure engineering designs.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Strength of Material: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Unit-I: Compound Stress and Strains (Short Question)
Q1. What do you mean by stress?
Ans. Stress is the amount of resistance to deformation that a body offers per unit of its surface.
Q2. What is strain ?
Ans. Strain is defined as the difference between the original and changed dimensions of a body.
Q3. What do you mean by shear strain ?
Ans. Shear strain is a dimensionless quantity that is defined as the change in the element’s right angle, measured in radians.
Q4. Explain the following terms:
a. Youngs modulus, and
b. Modulus of rigidity.
Ans. a. Young’s Modulus: It is the ratio of either compressive stress to compressive strain or between tensile stress and tensile strain.
b. Modulus of Rigidity: It is defined as the ratio of shear stress to shear strain.
Q5. Define bulk modulus of elasticity.
Ans. The ratio of normal stress to volumetric strain is known as the bulk modulus of elasticity.
Q6. Define strain energy.
Ans. A body stores energy known as strain energy as a result of the work the load does to strain the material therein.
Q7. Differentiate between strain energy and shear strain energy.
Ans.
| S. No. | Strain Energy | Shear Strain Energy |
| 1. | Energy due to change in size. | Energy due to change in shape. |
| 2. | This is caused by normal stress acting on the material. | This is caused by shear stresses acting on the material. |
Q8. What do you mean by resilience ?
Ans. Resilience is the amount of strain energy a body can withstand before reaching its elastic limit under external load.
Q9. Explain the term proof resilience.
Ans. Proof resilience is the greatest strain energy that can be held in a body up to the elastic limit.
Q10. Define the modulus of resilience.
Ans. Modulus of resilience is defined as the proof resilience of a material per unit volume.
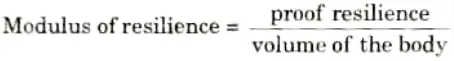
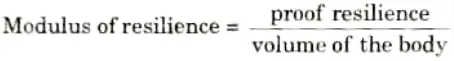
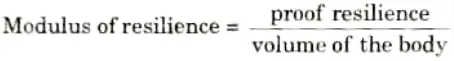
Q11. What is the difference between impact loading and gradual loading ?
Ans. The greatest stress that can be created during impact loading is twice as much as it is during progressive loading.
Q12. What is proof load ?
Ans. A proof load is the maximum force that a body can withstand before permanently deforming.
Q13. What are principal stresses and strains ?
Ans. Principal Stresses: Three planes that are mutually perpendicular and on each of which the resulting stress is entirely normal exist in complex systems of loading. They are referred to as principle planes, and principal stresses are the typical stresses that exist across these planes.
Principal Strain: Possible maximum and minimum normal strains at a certain location on a structure element. At the orientation where major strain occurs, shear strain is zero.
Q14. Explain Mohr’s circle.
Ans. When an element is subjected to two perpendicular loads, Mohr’s circle is a graphical approach for determining the normal and shear stresses on any interface of the element.
Q15. What do you mean by major principal plane and major principal stress ?
Ans. The major principal plane carries the most normal stress, and the major primary stress operating on it is referred to as the major principal stress.
Q16. What do you mean by minor principal plane and minor principal stress ?
Ans. The minor principle plane carries the least amount of normal stress, and the minor principal stress is the stress that is acting on it.
Q17. What is Hooke’s law ? Explain.
Ans. Hooke’s Law: It states, “When a material is loaded, within its elastic limit, the stress is proportional to the strain.” Mathematically
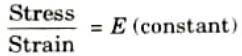
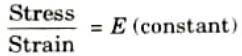
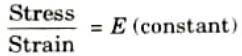
It may be noted that Hooke’s law equally hold good for tension as well as compression.
Q18. What are thermal stress and thermal strain ?
Ans.



Thermal stress is also known as temperature stress and thermal strain is also known as temperature strain.
Q19. If shear stress τ is induced in shaft due to torque T, then what will be the value of maximum normal stress induced in the shaft ?
Ans. The maximum normal stress is given as,
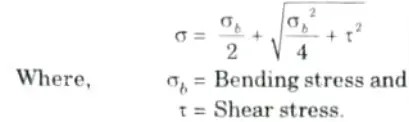
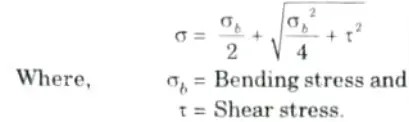
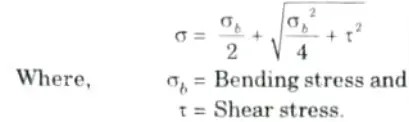
Q20. How does the complimentary shear stress affects the anisotropic materials ?
Ans. Complementary shear stress may cause anisotropic materials to fail prematurely.
Q21. When does the principle of superposition is not applicable to materials ?
Ans. Materials with non-linear stress-strain properties that do not obey Hooke’s law are not subject to the superposition principle.
Q22. Why are stresses called tensor ?
Ans. Stresses are called tensor because they can produce strain in all three directions.
Q23. Draw Mohr’s circle for pure shear in a two-dimensional stress field.
Ans.
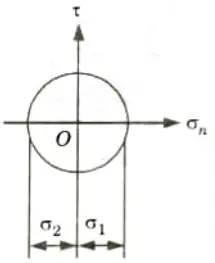


Unit-II: Beams and Torsion (Short Question)
Q1. What do you mean by bending stresses ?
Ans. Bending stresses are the stresses brought on by a bending moment.
Q2. Write down the bending equation for the beam.
Ans. The bending equation is given by,
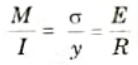
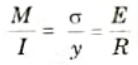
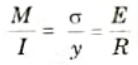
Q3. Define pure bending.
Ans. Pure bending is the process of a beam bending or attempting to bend into a circular arc while being subjected to a continuous bending moment.
Q4. What is neutral axis ?
Ans. The line where the neutral layer and the transverse section cross is referred to as the neutral axis.
Q5. What do you mean by composite beams ?
Ans. A composite beam is one that is composed of two or more materials that are thought to be rigidly coupled to one another and behave as a single unit.
Q6. Define neutral surface.
Ans. The neutral surface of a beam is defined as its surface when there are no bending stresses, which means it is neither in tension nor in compression.
Q7. Write down any two assumptions of simple theory of bending?
Ans. Following are the two assumptions of simple theory of bending:
- a. The material of beam is homogeneous.
- b. A plane before bending remains plane after bending.
Q8. Define elastic curves.
Ans. The elastic curve is a curve that forms when a weight acts on the neutral axis.
Q9. What are the different methods of finding slope and deflection of cantilever beam ?
Ans. Following are the different methods to determine the deflection of beams:
- a. Moment area method.
- b. Macaulay’s method.
- c. Double integration method.
- d. Conjugate beam method.
Q10. What are flitched beam and fixed beam ?
Ans. Flitched Beam: Flitched beams, such as hardwood beams strengthened by steel plates, are formed of two different materials.
Fixed Beam: A fixed beam is a beam that is designed to have both ends remain in a horizontal position.
Q11. Define continuous beam.
Ans. A continuous beam is one which is supported on more than two supports.
Q12. Define point of contraflexure.
Ans. A point of contraflexure is a point where the curvature of the beam changes sign.
Q13. What are the advantages of fixed beams over simply supported beams?
Ans. Following are the advantages of a fixed beam over a simply supported beam:
- a. A fixed beam’s maximum deflection is lower than a simply supported beam’s for a given loading.
- b. A fixed beam has zero slope at both ends.
- c. The beam is stronger and more steady.
Q14. Define torsion.
Ans. When a structural member is loaded by couplings that cause rotation about its longitudinal axis, it twists, which is known as torsion.
Q15. What are the main assumptions taken to derive the torsion equation?
Ans. Assumptions taken to derive the torsion equation are as follows:
- 1. The material is homogeneous and isotropic.
- 2. The shaft is circular in section.
- 3. The cross-section of the shaft remains uniform throughout.
- 4. The shaft is subjected to pure torque only.
Q16. What are the different torques acted on the shaft during power transmission ?
Ans. Shaft is subjected to following torques during power transmission:
- a. Driving torque at the input end.
- b. Resisting torque at the output end.
Q17. Write down the torsion equation for circular shafts.
Ans. The torsion equation is given by,
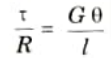
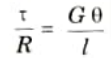
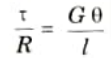
Q18. Define modulus of rupture.
Ans. The maximal fictional shear stress determined by the torsion formula using the maximum torque discovered experimentally to break a shatter is known as the modulus of rupture.
Q19. Write down any two assumptions made for a circular shaft subjected to torsion.
Ans. Following assumptions are made for a circular shaft subjected to torsion:
- a. The twist along the length of shaft is uniform throughout.
- b. The material of shaft is uniform throughout.
Q20. What do you mean by polar modulus ?
Ans. The ratio of the polar moment of inertia to the shaft’s radius is known as the polar modulus.
Q21. What do you mean by strength of a shaft ?
Ans. The maximal torque or power that a shaft can convey is referred to as its strength.
Q22. What do you understand by the term torsional rigidity ?
Ans. The polar moment of inertia of the shaft and its stiffness modulus are combined to form the shaft’s torsional rigidity.
Q23. What is flexural rigidity ?
Ans. Flexural rigidity is the stiffness of a material when subjected to bending.
Q24. Compare the strength of hollow and solid shaft.
Ans. Let us assume that both the shafts have same length, material, weight and hence the same maximum shear stress.
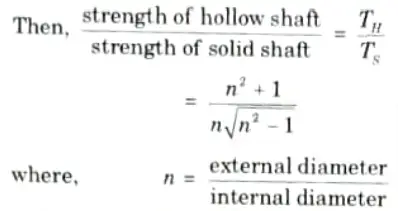
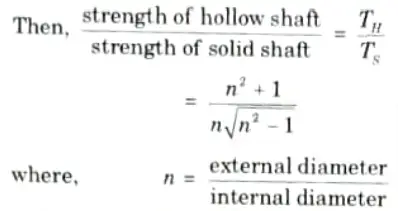
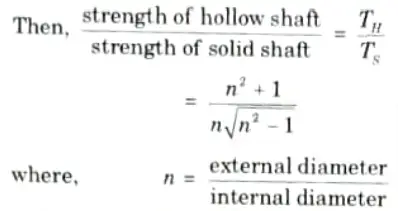
Since, n is always greater than 1. Hence, strength of hollow shafts is greater than solid shaft.
Q25. What is the difference between bending moment and twisting moment ?
Ans.
| Sending Moment | Twisting Moment |
| It is a moment that tends to bend a body in relation to its normal axis when it is applied in this way. | It is a moment that tends to cause a body to rotate around its axis when it is applied. |
Q26. Which method is used to determine the deflection of beam under several loads?
Ans. The deflection under various loads is calculated using Macaulay’s approach.
Q27. Which methods are used to determine deflection under single load ?
Ans. Deflection under a single load is calculated using the moment area method and the double integration method.
Q28. Write relation for maximum deflection and slope for simply supported beam subjected to uniformly distributed load over the whole span.
Ans. For maximum deflection,
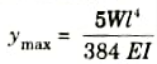
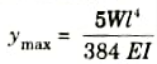
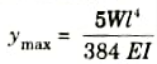
For maximum slope,
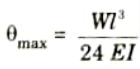
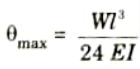
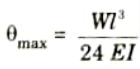
Q29. How differential equation of elastic curve is used to find slope and deflection of beam ?
Ans. The slope and beam deflection are determined by the differential equation’s first and second integrations, respectively. Boundary conditions are used to find the integration constants.
Unit-III: Springs, Columns and Struts (Short Question)
Q1. What is spring ? What are different types of spring?
Ans. Spring: Springs are elastic components that deform when subjected to force but return to their original shape once the force is withdrawn.
Types of Spring:
Following are the different types of springs :
a. Helical springs, b. Leaf springs,
c. Torsion springs, d. Circular springs,
e. Belleville springs, and f. Flat springs.
Q2. What do you mean by leaf spring ?
Ans. A leaf spring is constructed from many parallel plates that are strapped together and have the same width and thickness but differ in length.
Q3. What is bending spring ?
Ans. A spring is referred to as a bending spring when it only experiences bending and gains resilience as a result.
Q4. What do you mean by resilience of the spring ?
Ans. A spring is referred to as a bending spring when it only experiences bending and gains resilience as a result.
Q5. What are the various stresses induced in closed coil helical spring?
Ans. Following are the various stresses induced in closed coil helical spring:
- a. Direct shear stress, and
- b. Torsional stress.
Q6. Define stiffness,
Ans. The load necessary to produce a unit of deflection is what determines a spring’s stiffness.
Q7. Define spring index.
Ans. The ratio of mean coil diameter to wire diameter is known as the spring index. C is typically used to represent it.
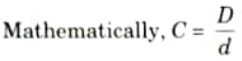
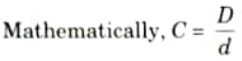
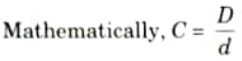
Q8. Write the relation for axial deflection for open coil helical spring subjected to axial twist.
Ans. Axial deflection,
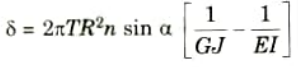
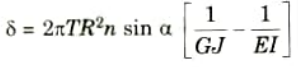
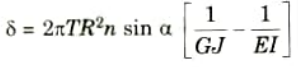
Q9. What are closed helical springs?
Ans. Closed helical springs are ones whose angle of helix is so narrow that, if the spring’s axis is vertical, the coils may be thought to be in a horizontal plane.
Q10. What is the difference in analysis of closed and open coiled springs?
Ans.
| S. No. | Closed Coiled Springs | Open Coiled Springs |
| 1. | It is known as torsion spring. | It is known as compression spring |
| 2. | Torsional stress is extremely high. | Torsional stress is extremely low. |
Q11. Write down the formula for proof load in a leaf spring.
Ans. Proof load in a leaf spring is given as,
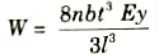
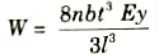
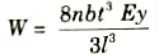
Q12. What is column ?
Ans. A column is a long, thin vertical bar or vertical part that is securely fastened at both ends and is under an axial compressive load.
Q13. Define strut.
Ans. A strut is a thin bar or member that is not vertical and that has one or both ends that are hinged or pin connected.
Q14. What is the difference between column and strut ?
Ans.
| S. No. | Column | Strut |
| 1. | It is a vertical member subjected to axial compressive load. | lt is an inclined member subjected to axial load. |
| 2. | It fails in compression. | It fails due to buckling. |
Q15. What is slenderness ratio and equivalent length of a column ?
Ans. Slenderness Ratio: It is the ratio of the column’s unsupported length to its minimal gyrating radius at its cross-sectional ends. Its symbol is “k,” and it has no dimensions.
Equivalent Length: Equivalent length, effective length, or simply column length are all terms used to describe the separation between adjacent points of inflexion. Every end of a column that is free to spin as well as any location where the axis changes have points of inflexion.
Q16. What is crippling load ?
Ans. The crippling or buckling load is the maximum limiting load at which the column tends to experience lateral displacement or buckles.
Q17. What do you understand by the term “buckling” of columns?
Ans. When a long column is compressed, it experiences compressive stress. If the load is continuously raised, the column will eventually reach a point where it begins to bend. We refer to this bending as buckling.
Q18. Define safe load.
Ans. The safe load, which is significantly less than the buckling load, is the load that a column is actually subjected to.
Mathematically,
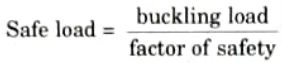
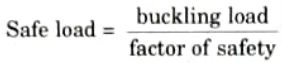
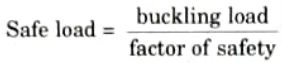
Q19. Write down Euler’s formula for calculation of critical load ?
Ans.
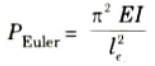
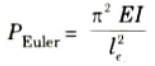
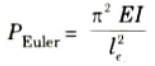
Q20. What are the limitations of Euler’s formula ?
Ans. Limitations for the use of Euler’s formula:
- i. It is applicable to an ideal strut only.
- ii. It takes no account of direct stress.
Q21. Write the relation for axial deflection for open coil helical spring subjected to axial twist.
Ans. Axial deflection,
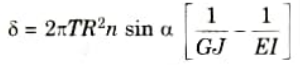
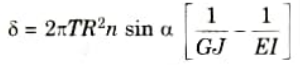
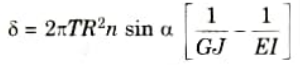
Q22. How will you define the strength of column ?
Ans. Strength of column is defined as the capacity of column to resist load.
Unit-IV: Cylinders and Spheres (Short Question)
Q1. What is thin cylinder ?
Ans. The cylindrical vessel is referred to as a thin cylinder if the thickness of its wall is less than one twentieth of its interior diameter.
Q2. Define longitudinal stress.
Ans. Laminar stress is defined as the force operating along the length of the cylinder, or in the longitudinal direction.
Q3. Establish the relation between circumferential stress and longitudinal stress.
Ans.
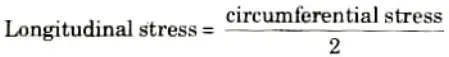
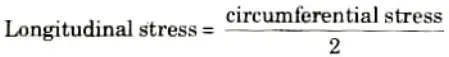
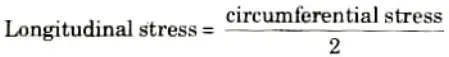
Q4. What is the difference between thin and thick cylinder ?
Ans.
| S. No. | Thick Cylinder | Thin Cylinder |
| 1. | The thickness of cylindrical vessel is greater than 1/20 of its internal diameter. | The thickness of the cylindrical vessel is less than 1/15 to 1/20 of its internal diameter. |
| 2. | The stresses are not uniform rather it varies along the thickness. | Stresses are assumed to be uniform throughout the wall thickness. |
Q5. What do you understand by autofrettage ? Explain it in brief.
Ans. A pressure vessel is put under extreme pressure during the autofrettage process, which causes interior parts of the part to give plastically. internal compressive residual stresses that appear after the pressure is released.
Q6. What is wire winding of thin cylinder ?
Ans. A thin cylinder is strengthened against internal pressure through the technique of “wire winding,” in which wire is wound around it under tension as the cylinder wall is compressed.
Q7. Write down any two assumptions of Lame’s theory.
Ans. Following assumptions are made in Lame.s theory:
- a. Material is homogeneous and isotropic.
- b. Material is stressed within elastic limit.
Q8. How can we obtain the variation in the radial as well as circumferential stresses across the thick cylinder ?
Ans. With the aid of Lame’s theory, it is possible to determine how the radial and circumferential stresses vary across the thick cylinder.
Q9. Explain the purpose of compounding thick cylinders.
Ans. The goal of compounding the cylinders is to increase a single cylinder’s capacity to withstand pressure.
Q10. Why is it necessary to strengthen the cylinder longitudinally ?
Ans. The likelihood of the cylinder bursting longitudinally is greater than the likelihood of the cylinder failing circumferentially. Consequently, longitudinal cylinder strengthening is required.
Q11. Why is wire winding used in thin cylinders ?
Ans. Wire winding is used in thin cylinders for following purposes:
- a. To increase the pressure carrying capacity of the cylinder.
- b. To reduce the chances of longitudinal burst.
Q12. At which part of the thick cylinder the hoop stress is maximum and minimum ?
Ans. In a thick cylinder, the hoop stress is highest at the inner circumference and lowest at the outside circumference.
Q13. Why spherical containers are more preferred to store the gases in comparison to cylindrical containers ?
Ans. Spherical containers are more preferred to store gases since their pressure is continuous throughout.
Unit-V: Curved Beam and Unsymmetrical Bending (Short Question)
Q1. Give the classification of curved bars.
Ans. The curved bars may be broadly grouped into the following two categories:
- a. Bars with a small initial curvature, and
- b. Bars with a large initial curvature.
Q2. What do you mean by neutral axis ?
Ans. A layer inside the beam known as the neutral axis experiences neither compressive nor tensile stress.
Q3. What is Winkler-Bach theory ?
Ans. When bending deeply curved beams and a simple bending formula is not applicable, Winkler-Bach theory is employed.
Q4. What is unsymmetrical bending?
Ans. Unsymmetrical bending is a term used to describe bending where the plane of stress is not constrained by the major centroidal axis of the cross-section.
Q5. Give the reasons of unsymmetrical bending.
Ans. Following are the two reasons of unsymmetrical bending:
- 1. The section is symmetrical but the load line is inclined to both the principal axes.
- 2. The section itself is unsymmetrical and the load line is along any centroidal axis.
Q6. Differentiate between pure and unsymmetrical bending.
Ans.
| S. No. | Pure Bending | Unsymmetrical Bending |
| 1. | A member is considered to be in pure bending if it is subjected to equal and opposite couples acting in the same longitudinal planes. | Unsymmetrical bending is defined as bending where the plane of loading or the plane of bending does not contain the main centroidal axis of the cross-section. |
Q7. State the parallel axes theorem for product of inertia.
Ans. A lamina’s moment of inertia about any axis in its plane is equal to the product of its area and the square of the distance between its two axes plus its moment of inertia about its parallel centroid axis.
Q8. What do you mean by principal axes ?
Ans. The two axes are referred to be the major axes if the two axes around which the product of inertia is discovered are such that the product of inertia becomes zero.
Q9. Explain section modulus and its significance.
Ans. i. Section Modulus: The ratio of a section’s moment of inertia around the neutral axis to the distance of the outermost layer from the neutral axis is what is meant by this word. It is denoted by Z.
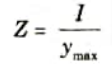
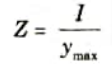
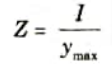
Significance: It is direct measure of the strength of the beam.
ii. Modular Ratio: The Young’s modulus of elasticity of two different materials used in composite construction is measured as it.
Q10. What is shear centre ?
OR
Define shear center and its importance.
Ans. The junction of the bending axis with the plane of transverse section defines the shear centre.
Importance: Shear centre is a location where there won’t be any bending of the section if the external force passes through it.
Q11. Write down some applications of curved beam with large initial curvature.
Ans. Applications of curved beam with large initial curvature are as follows:
- a. Crane hook,
- b. Making of flyover trusses, and
- c. Big structures of trusses.
Q12. Why is simple bending formula not applicable for deeply curved beams ?
Ans. Deeply curved beams cannot be bent using the simple bending formula because the neutral and centroidal axes are not parallel.
Q13. Why is trapezoidal section very commonly used in crane hooks ?
Ans. The neutral axis of the beam was moved closer to and towards the centre of curvature because of the trapezoidal cross-section. As a result, the hook’s ability to withstand bending stresses improves, as does its capacity to support weight.
Q14. Where does the maximum stress occur in the unsymmetrical bending ?
Ans. In a location that is furthest from the neutral axis, the most stress is felt.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Strength of Material Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Strength of Material Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One View) | Student Result |
