Quantum Notes will help you prepare for Strength of Materials. Find crucial questions that appear regularly in Aktu Btech exams. Get the competitive advantage you require! Unit-1 Compound Stress and Strains
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Strength of Material: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. Define stress and also classify it.
Ans. A. Stress:
- 1. Stress is the amount of resistance to deformation that a body offers per unit of its surface. The term “load” or “force” refers to the outside force operating on the body.
- 2. Mathematically, stress
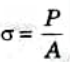
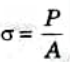
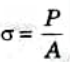
Where, σ = Stress (also called intensity of stress), P = External force or load, and A = Cross-sectional area.
- 3. Stress is expressed in N/m2.
- 4. There are two types of stresses :
- a. Normal stress, and
- b. Shear stress.
a. Normal Stress:
- 1. It is the stress which acts in a direction perpendicular to the area. It is represented byσ.
- 2. The normal stress is further divided into tensile stress and compressive stress.
i. Tensile Stress:
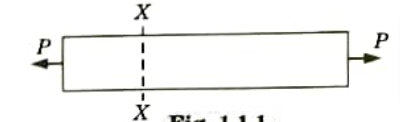
- 1. Tensile stress is the strain that a body experiences when it is subjected to two equal and opposite pulls that cause it to lengthen (Fig.).
- 2. The tensile stress acts normal to the area and it pulls on the area.


ii. Compressive Stress:
- 1. Compressive stress is the tension created in a body when it experiences two equal and opposite pushes that cause the body’s length to shrink (Fig.).



- 2. The compressive stress acts normal to the area and it pushes on the area.
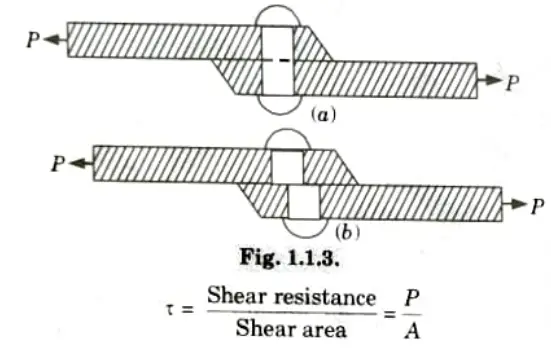
b. Shear Stress:
- 1. Shear stress is the tension created in a body when two equal and opposing pressures operating tangentially across the resistive section are applied; as a result, the body tends to shear off across the section (Fig.).
- 2. It is represented by 𝞃.


Q2. At a point in a beam the normal stress along the length is 80 Nmm2, The shear stress at that point is positive (CW) of magnitude 35 N/mm2. Find the stresses on a plane whose normal is inclined at 30° to the longitudinal axis. Also find the principal stresses and planes on which they act.
Ans.
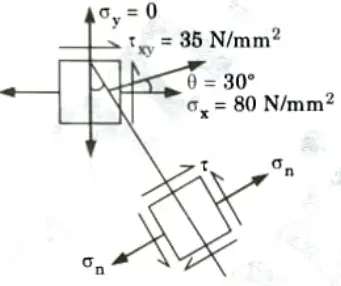


1. Normal stress is given by,
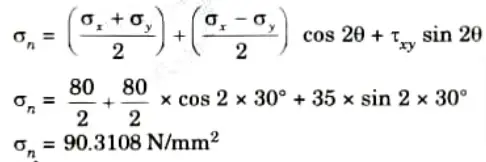
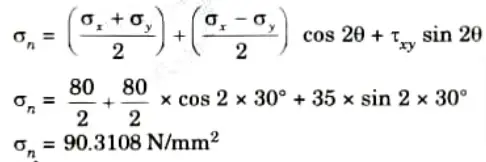
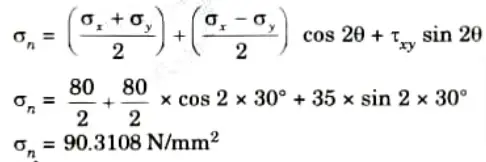
2. Shear stress is given by,
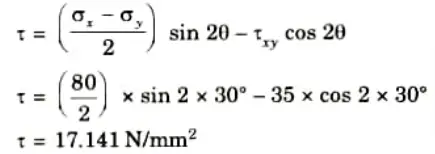
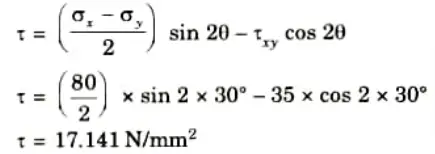
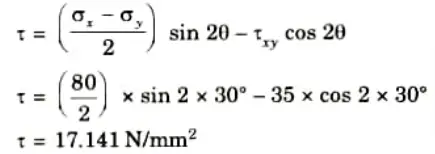
3. Principal Stresses are given by,
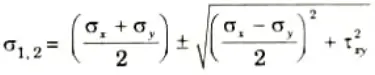
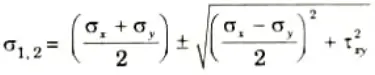
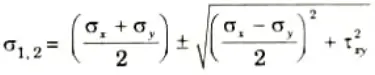
i. Major principal stress,
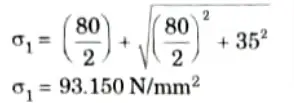
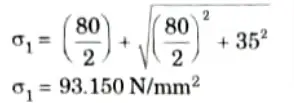
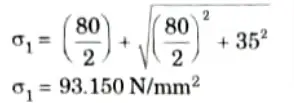
ii. Minor principal stress,
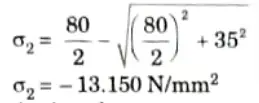
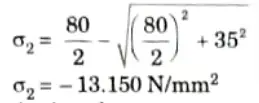
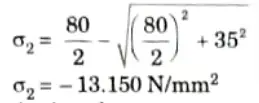
4. Plane of inclination is given by,
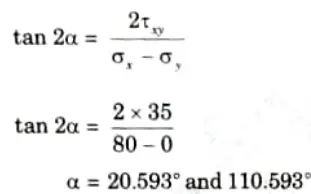
Q3. What do you understand by thermal stresses ? Explain.
Ans.
- 1. The stresses induced in a body due to change in temperature are known as thermal stresses.
- 2. Consider a body which is heated to a certain temperature.



- 3. If the rod is free to expand, then extension of the rod is given by
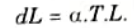
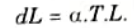
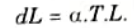
- 4. If the ends of the body are fixed to rigid supports, so that its expansion is prevented, then compressive stress and strain will be set up in the rod. These stresses and strains are known as thermal stresses and thermal strain.
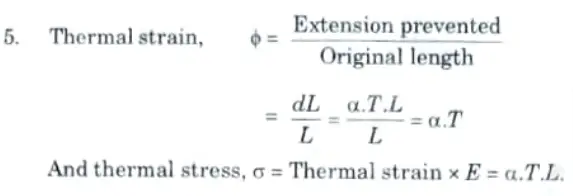
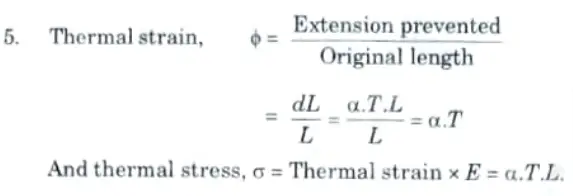
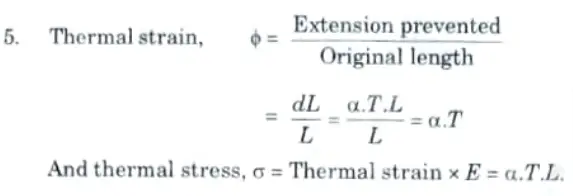
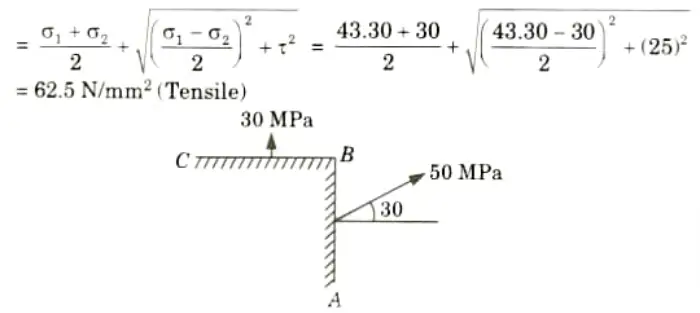
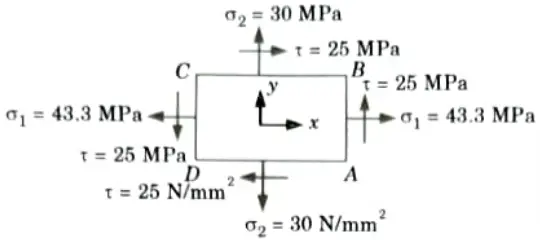
Q4. At a point in a material under stress, the intensity of the resultant stress on a certain plane is 50 MPa (tensile) inclined at 30° to the normal of that plane. The stress on a plane at right angle to this has a normal tensile component of intensity of 30 MPa, find:
i. The resultant stress on the second plane.
ii. The principal planes and stresses.
iii. The plane of maximum shear and its intensity.
Ans. Given: Resultant stress on plane AB = 50 MPa
Angle of inclination = 30°, Normal stress on plane BC= 30 MPa
To Find: i. The resultant stress on the second plane.
ii. Principal plane and stresses.
iii. Plane of maximum shear and its intensity.
1. The resultant stress 50 MPa on plane AB is resolved into normal and tangential stress.
The normal stress on plane AB = 50 x cos 30° = 43.30 N/mm2
The tangential stress on plane AB = 50 x sin 30° = 25 N/mm2
2. Resultant stress on the second plane BC
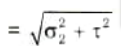
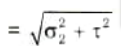
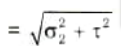
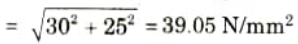
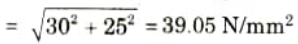
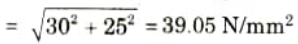
3. Major principal stress







5. The direction of principal stress,



Q5. Derive the expression for strain energy stored in a body when the load is applied gradually. Also write the expression for sudden load applied.
Ans.
- 1. Fig. shows load extension diagram of a body under tensile test upto elastic limit.
- 2. The tensile load P increases gradually from zero to the value of P and the extension of the body increases from zero to the value of x.
- 3. The load P performs work in stretching the body. This work will be stored in the body as strain energy which is recoverable after the load P is removed.
- 4. Let P = Gradually applied load, x = Extension of the body, A = Cross sectional area, L = Length of the body, V = Volume of the body, E Young’s modulus, U = Strain energy stored in the body, and 𝝈 = Stress induced in the body.
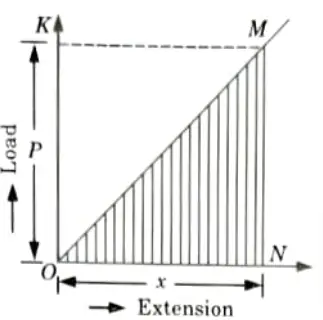


5. Now work done by the load = Area of load extension curve (Shaded area in Fig.)
= Area of triangle ONM



7. Substituting the values of P and x in eq. (1.13.1), we get
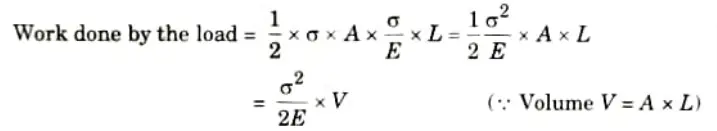
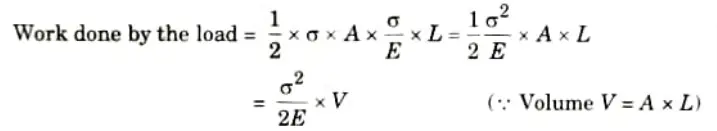
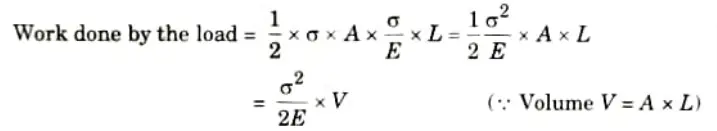
8. But the work done by the load in stretching the body is equal to the strain energy stored in the body.
Therefore, energy stored in the body,
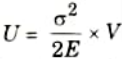
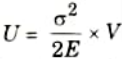
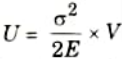
9. As the load is applied suddenly, the load Pis constant when the extension of the bar takes place.
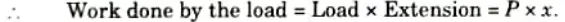
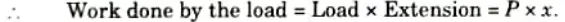
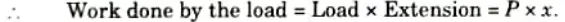
10. The maximum strain energy stored (i.e., energy stored upto elastic limit) in a body is given by






11. Equating the strain energy stored in the body to the work done, we get
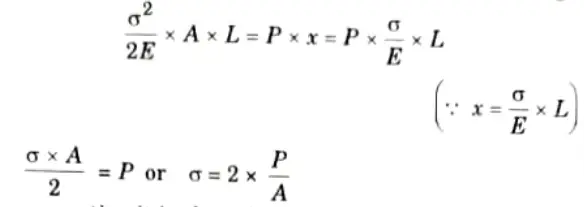
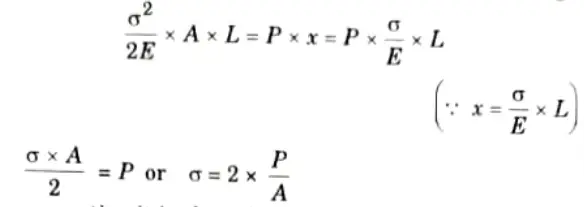
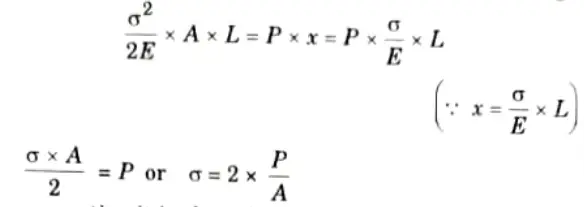
12. It is evident from the aforementioned equation that the greatest stress brought on by a load that is delivered suddenly is twice as much as the stress brought on by a load that is applied gradually.
Q6. A 1 m long bar of rectangular cross section 50 mm x 80 mm is subjected to an axial load of 1.2 kN. Determine the maximum stress and the strain energy developed in the bar if the load applied is:
i. Gradual,
ii. Sudden, and
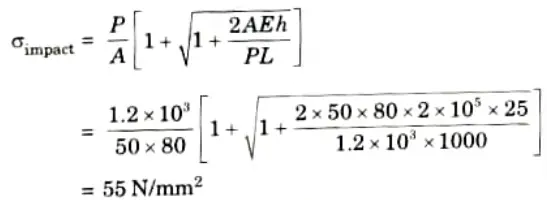
iii. Falls through a height of 25 mm.
Ans. Given: l = 1 m, P = 1.2 kN, Cross section 50 mm x 80 mm, h = 25 mm
Data Assumed: E =2 x 105 N/mm2
1. We know that,
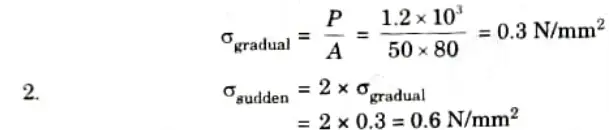
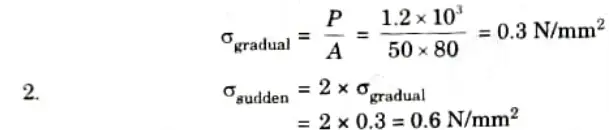
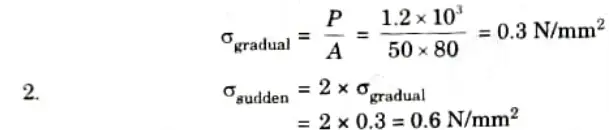
3. Maximum stress when load falls through a height


4. Strain energy in case of gradually applied load,
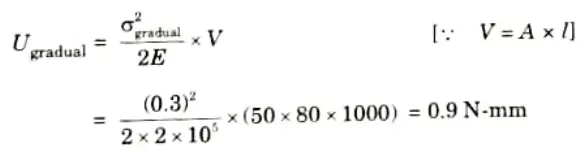
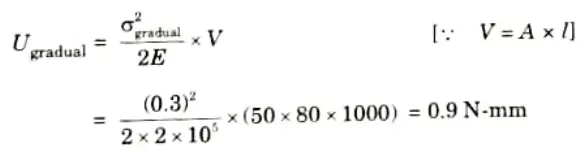
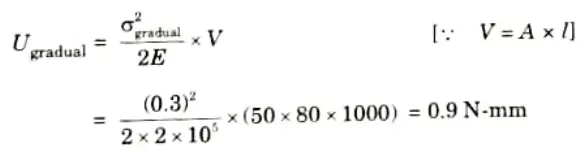
5. Strain energy in case of sudden applied load,
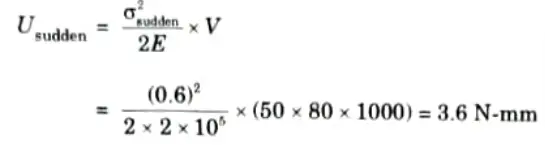
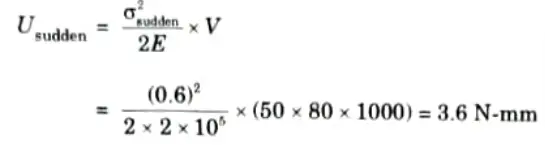
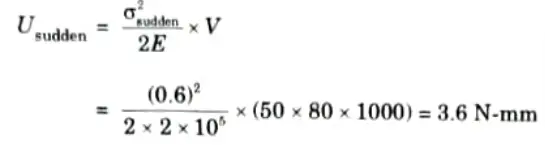
6. Strain energy in case of impact load,
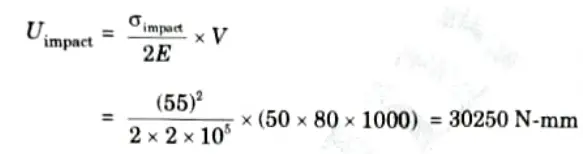
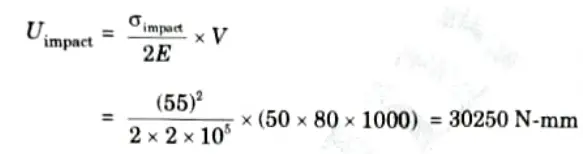
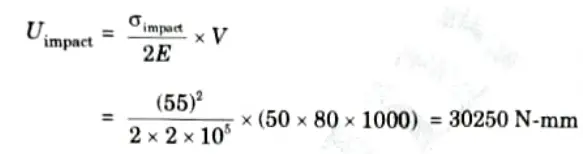



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Strength of Material Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Strength of Material Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One View) | Student Result |
