Looking for crucial Math-4 short questions for Btech AKTU? Check out our blog article that offers brief questions from all subjects to help you study for your examinations efficiently. Prepare to confidently tackle the arithmetic subjects!
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Math 4 (Mathematics 4): *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Unit -1 (Partial Differential Equations – 2 Marks Questions)
Q1. Find the particular integral of (D* + DD) 2 = sin (x+) where
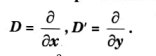
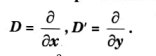
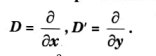
Ans:
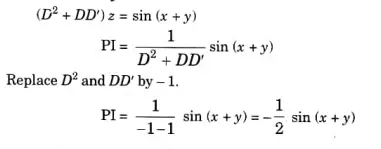
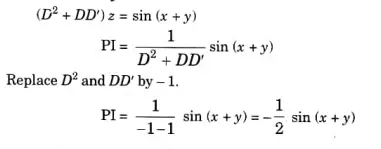
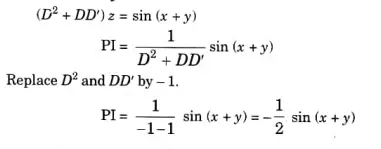
Q2. Find the particular integral of the following partial differential equation
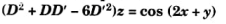
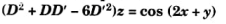
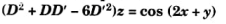
Ans:
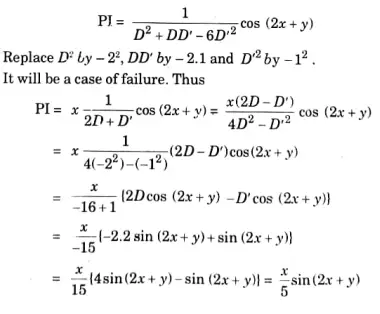
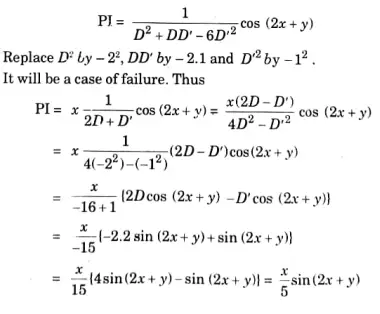
Q3. Solve: (D- 5D’+ 4)3z = 0
Ans:
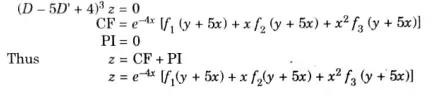
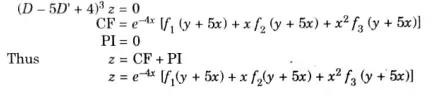
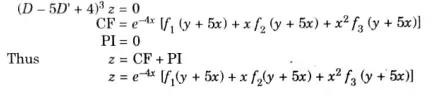
Q4. Solve: (D2-2D’) z = 0.
Ans:



Q5. Solve: (D3D’2+ D2D’3) z =0.
Ans:
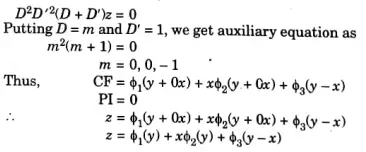
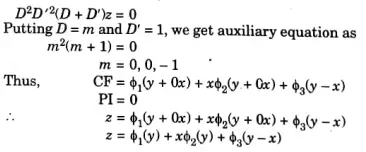
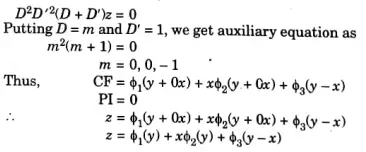
Q6. Solve the PDE (D-D’-1) (D+D’-2)z = e2x-y
Ans.
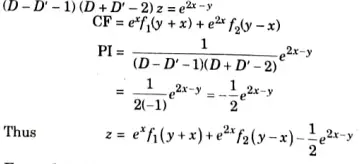
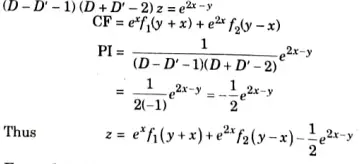
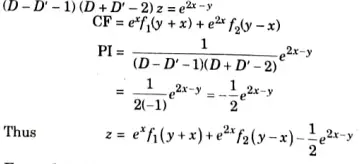
Q7. Formulate the PDE by eliminating the arbitrary function from
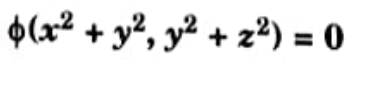
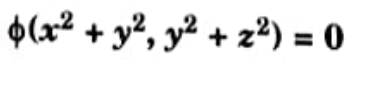
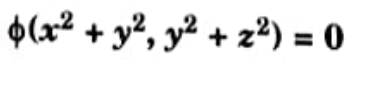
ANs.
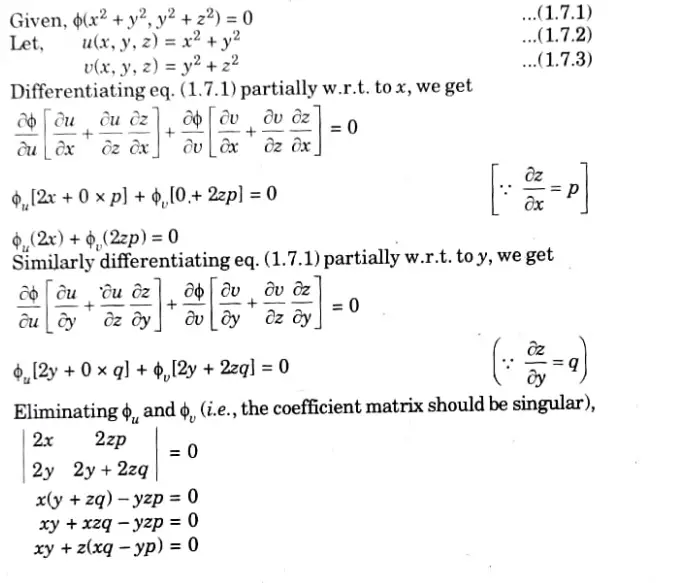
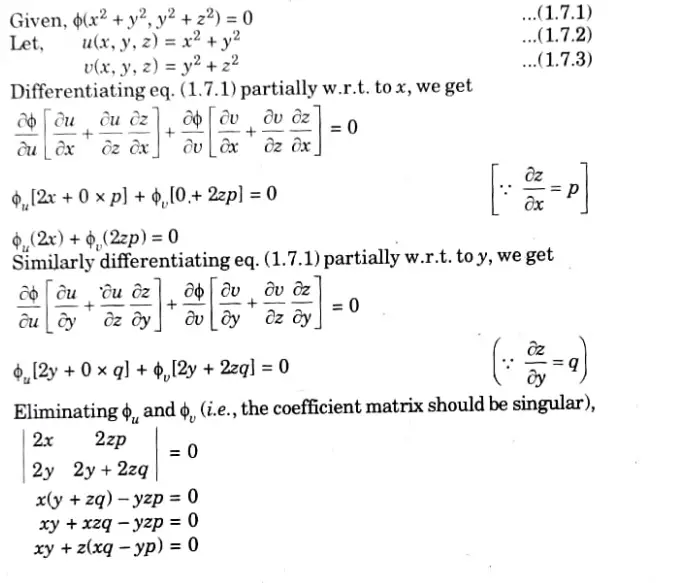
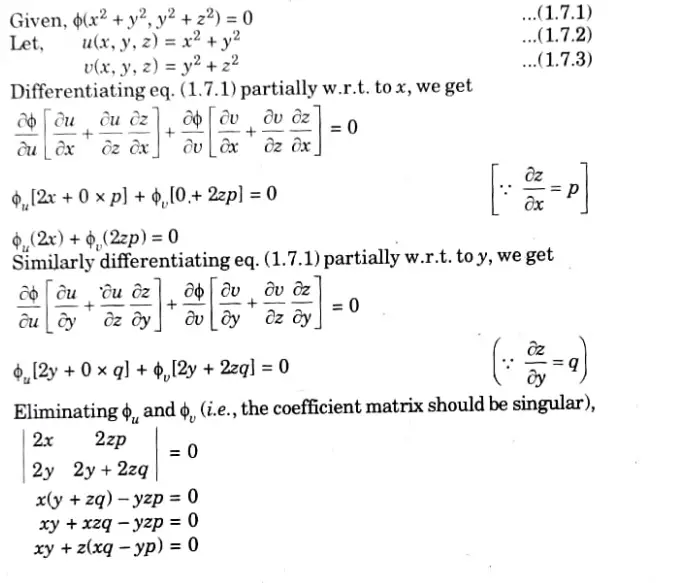
Q8. Solve p-q = 1.
Ans. The complete solution is z = ax +by + c where a -b=1 Hence z = ax + (a – 1)y +c is the desired solution.
Q9. Solve this
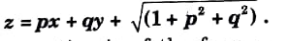
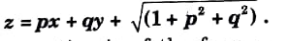
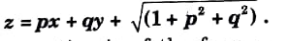
Ans.
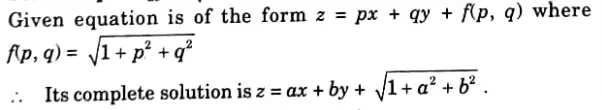
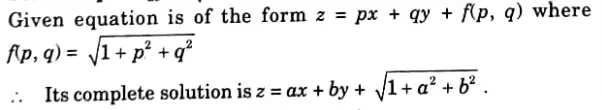
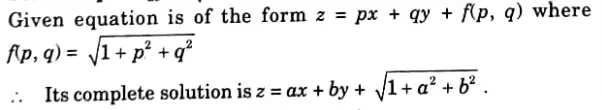
Q10. Find the particular integral of
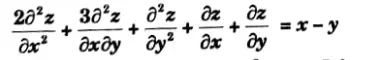
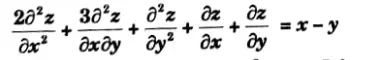
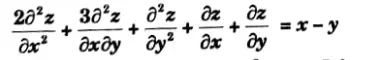
Ans.
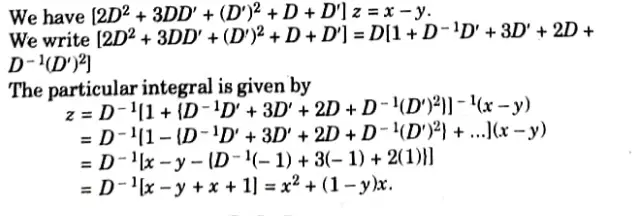
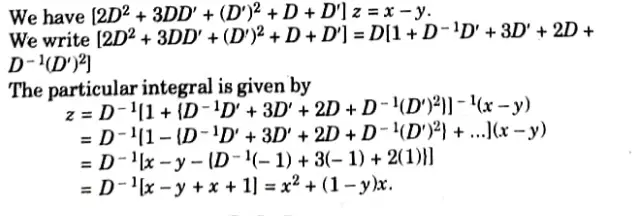
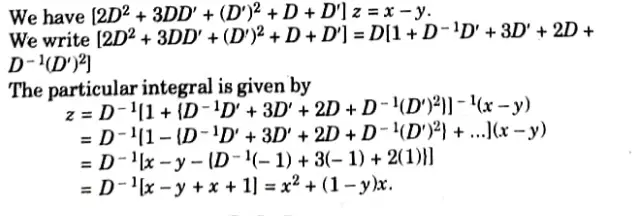
Unit-2 Application of Partial Differential Equations
Q1. For a second order Partial Differential Equation (PDE) in the function ‘u’ of two independent variables x, y given with usual symbols Auxx + Buxy + Cyy + F(u) = 0 then write the condition for type of the equation.
Ans.
- For a second order PDE
- Auxx + Buxy + Cyy + F(u) = 0 – 1
- Here, A, B, C are constants or continuous functions of x and y and A is positive.
- If B2-4 AC <0 then eq1 represents an elliptic equation.
- If B2-4AC = 0 then eq1 represents a parabolic equation.
- If B2-4AC>0 then eq. (2.1.1) represents the hyperbolic equation.
Q2. Classify the following differential equation in the first quadrant y2uxx – x2uyy = 0
Ans.
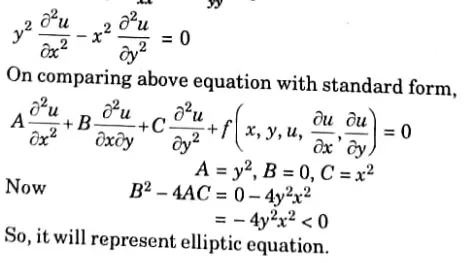
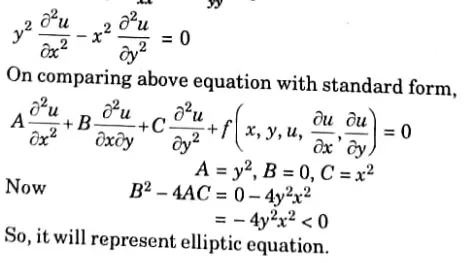
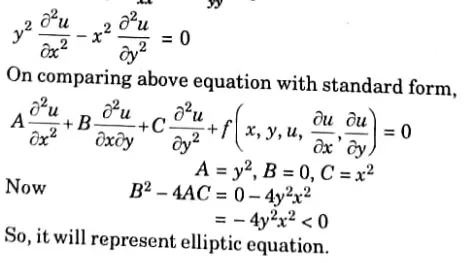
Q3. Classify the following partial differential equation
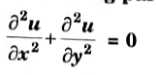
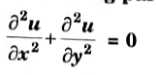
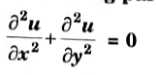
Ans. On comparing above equation with standard form,



Q4. Classify the equation uxx + 3uxy =uyy = 0
Ans.
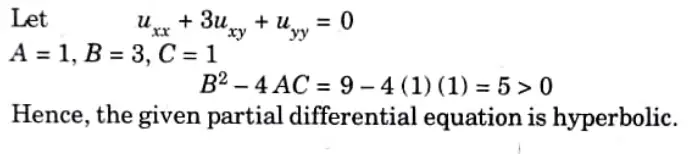
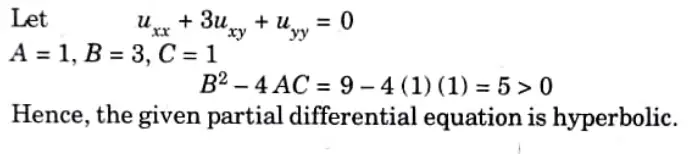
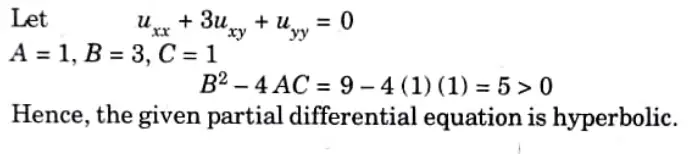
Q5. Solve using method of separation of variables.
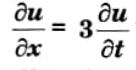
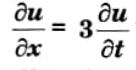
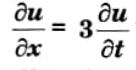
Ans.
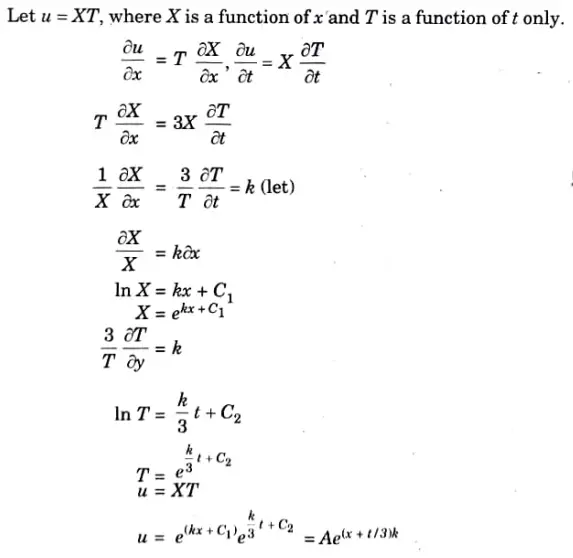
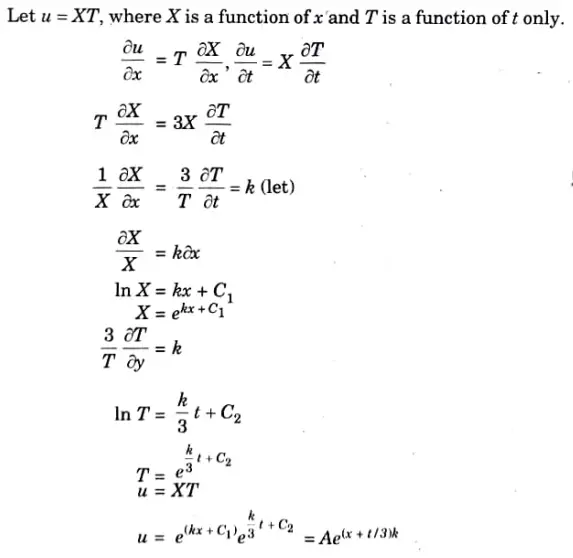
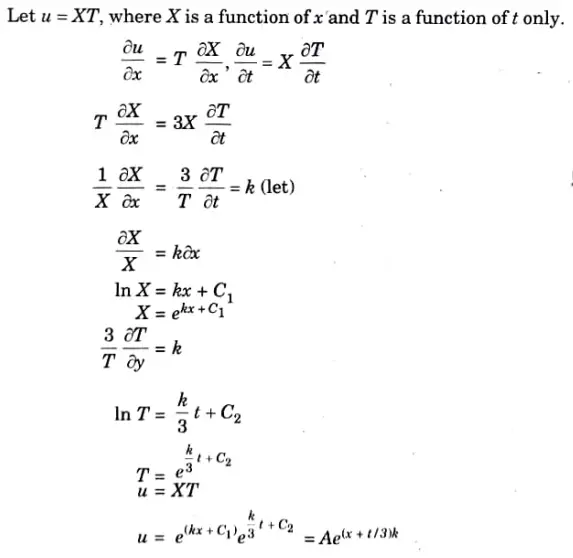
Q6. Write down the solution for the PDE
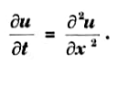
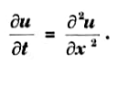
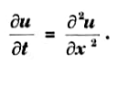
Ans.
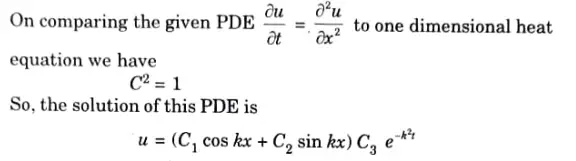
Q7. Find the steady state temperature distribution in a rod of 2m whose ends are kept at 30 °C and 70 °C respectively.
Ans.



Q8. Write two dimensional heat equation.
Ans.
Two dimensional heat equation is
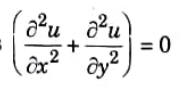
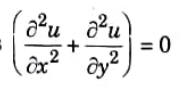
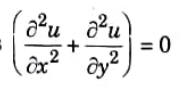
Q9. Write down transmission line equations.
Ans.
i. Telegraph equations:
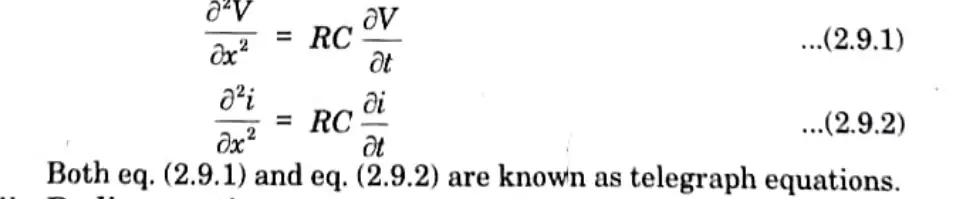
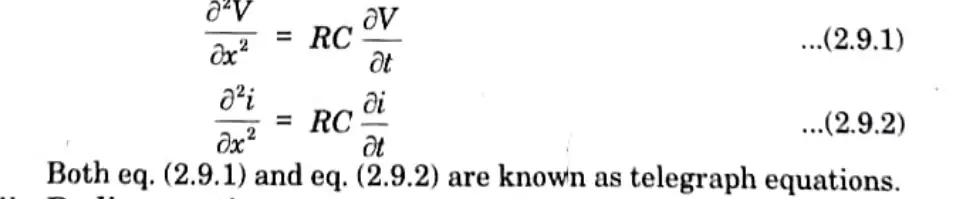
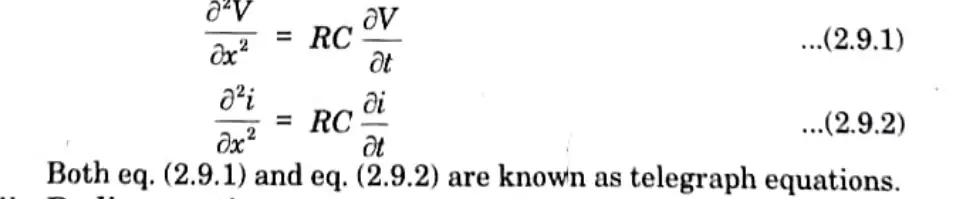
ii. Radio equations:
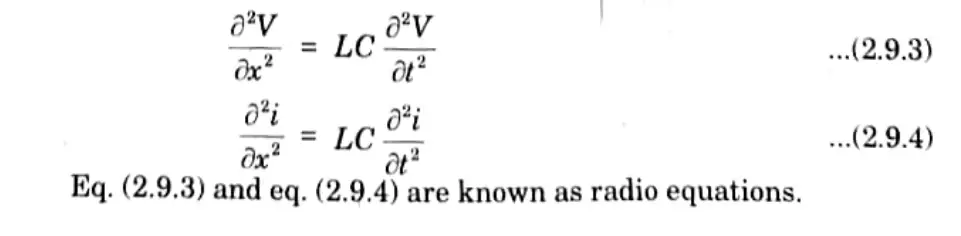
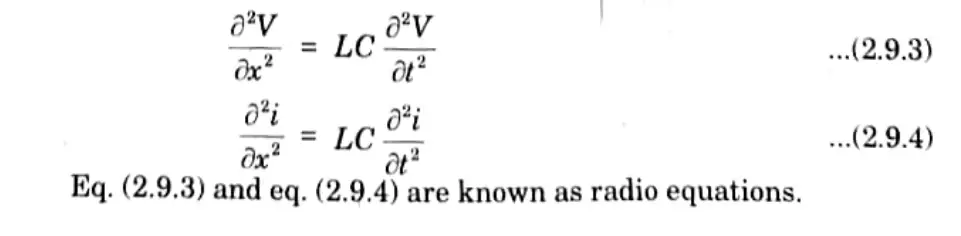
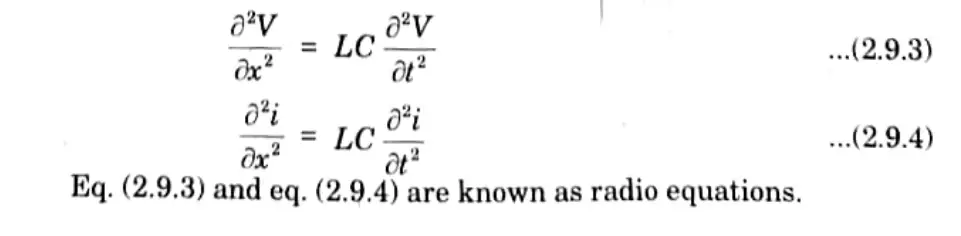
Q10. Write down the case (or equation) for submarine cable.
Ans.
. Transmission line equation is
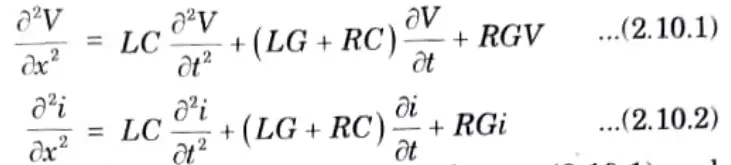
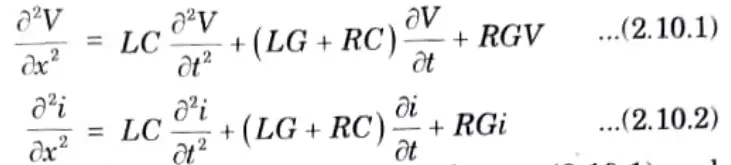
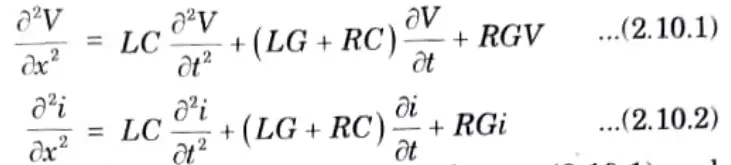
For submarine cables, L = C = 0 hence the eq. (2.10.1) and eq. (2.10.2) will reduce to
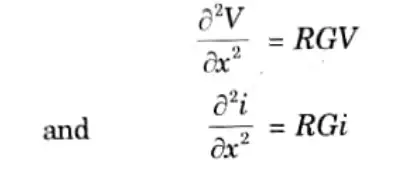
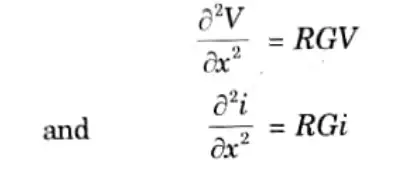
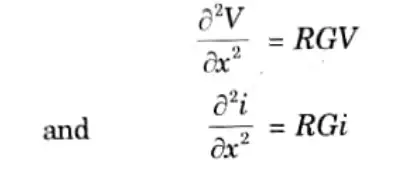
Q11. Specify with suitable examples the clarification of Partial Differential Equation (PDE) for elliptic, parabolic and hyperbolic differential equations.
Ans.
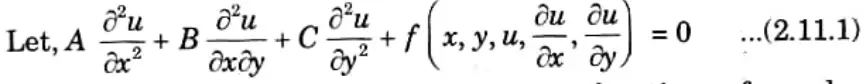
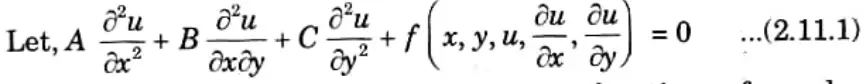
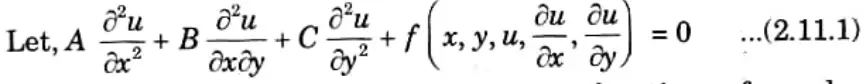
where A, B, C are constants or continuous functions of x and y possessing continuous partial derivatives and A is positive.
Now eq. (2.11.1) is
- Elliptic, if B2-4AC<0
- Hyperbolic, if B2 -44C>0
- Parabolic, if B2 -4AC = 0
Example : Consider partial differential equation as follows:
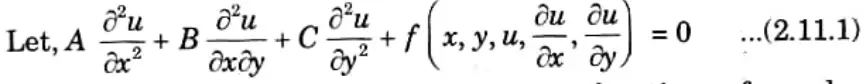
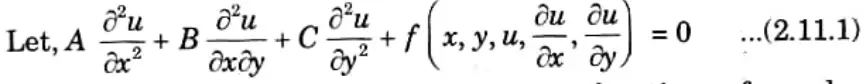
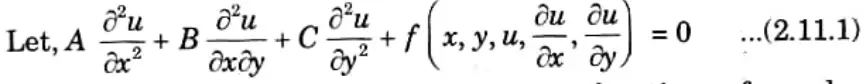
Unit 3 Statistical Techniques
Q1. What is the meaning of skewness?
Ans. The term skewness means lack of symmetry i.e When a distribution is not symmetric then it is called a skewed distribution and this distribution may be positively skewed or negatively skewed.
Q2. What do you understand by measure of kurtosis ? Discuss in brief.
Ans. Measure of kurtosis
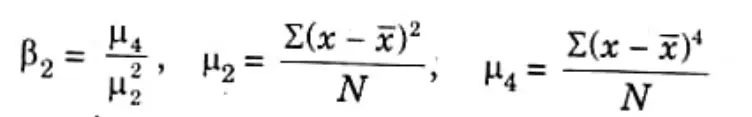
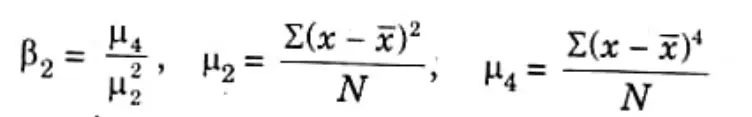
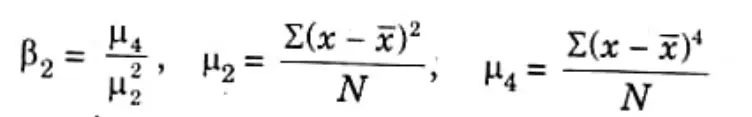



Q3. Discuss in brief the types of correlation.
Ans. Types of correlation:
1. Positive correlation: If a decrease in the value of one variable X results in a corresponding decrease in value of other variable Y on an average, the correlation is said to be positive.
2. Negative correlation: If the decrease in the values of one variable X results in the increase to a corresponding values of Y, the correlation between X and Y is said to be negative.
3. Linear correlation: When all the plotted point lies approximately on a straight line, then the correlation is said to be linear correlation.
4. Perfect correlation: If the deviation of one variable X is proportional to the deviation in other variable Y, then the correlation is said to be perfect correlation.
Q4. Define regression lines
Ans. A line of regre ssion is the straight line which gives the best fit in the least square to the given frequency
Q5. If covariance between x and y variable is 10 and the variance of x and y are respectively 16 and 9, find the coefficient of correlation.
Ans.



Q6. Write the normal equations to fit a curve y = ax2 + b by least square method. Ans. Normal equations for the given curve are:
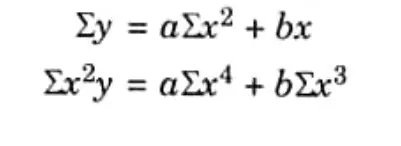
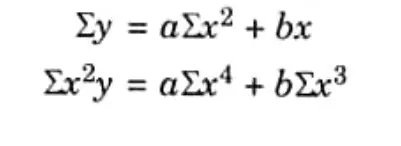
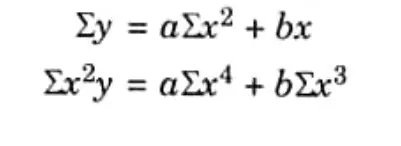
Q7. Write normal equation of
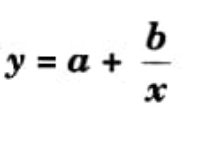
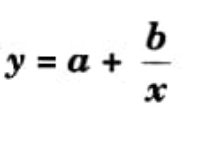
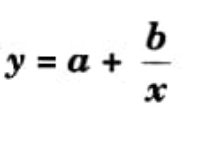
Ans.
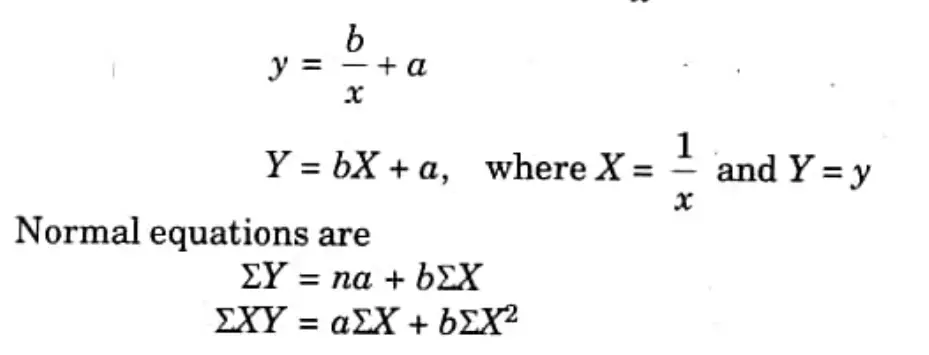
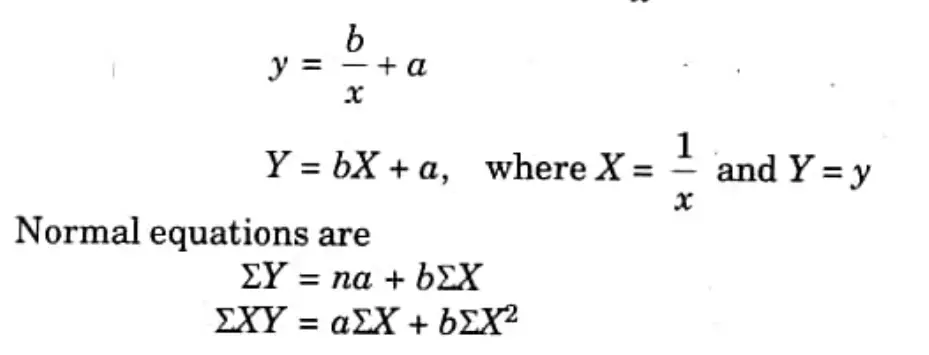
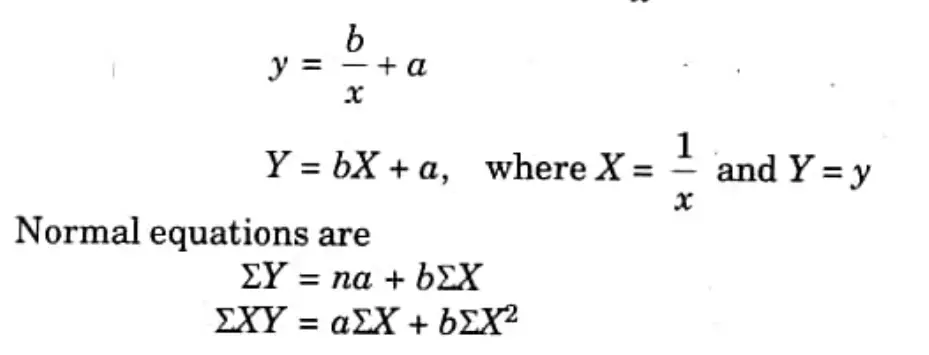
Q8. The regression equations calculated from a given set of observation for two random variables are x = -0.4y +6.4 and y=-0.6ar + 4.6.
Calculate mean values of x and y.
Ans.



Q.9. The first three central moments of a distribution are 0, 2.5, 0.7. Find the value of the moment coefficient of skewness.
Ans.



Q10. Differentiate between skewness & kurtosis.
| Skewness | Kurtosis |
| It Describes the tendency of a distribution that determines its symmetry about the mean. | Kurtosis mean the measure of the respective sharpness of the curve in the frequency distribution. |
| Skewness measures the degree of Lopsidedness in the distribution. | It measures the degree of tailedness in the distribution. |
Q.11. Fit the equation of straight line from the following data:
| x | 1 | 2 | 3 | 4 | 5 |
| y | 14 | 27 | 40 | 55 | 68 |
Ans.






Unit-4 Statistical Techniques II
Q1. Find the probability of getting sum as 9 when two dice are thrown.
Ans: Total number of possible ways of throwing two dice = 6×6=36
Number of ways getting 9, i.e., (3 +6),(4 +5), (5 + 4), (6+3) = 4
The required probability=4/36 = 1/9
Q2. From a pack of 52 cards, one is drawn at random. Find the probability of getting a king.
Ans:
A king can be chosen in 4 ways.
But a card can be drawn in 52 ways.
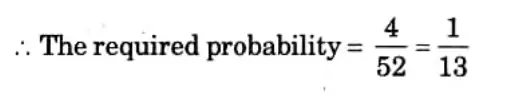
Q3. Solve this Problem
Ans.
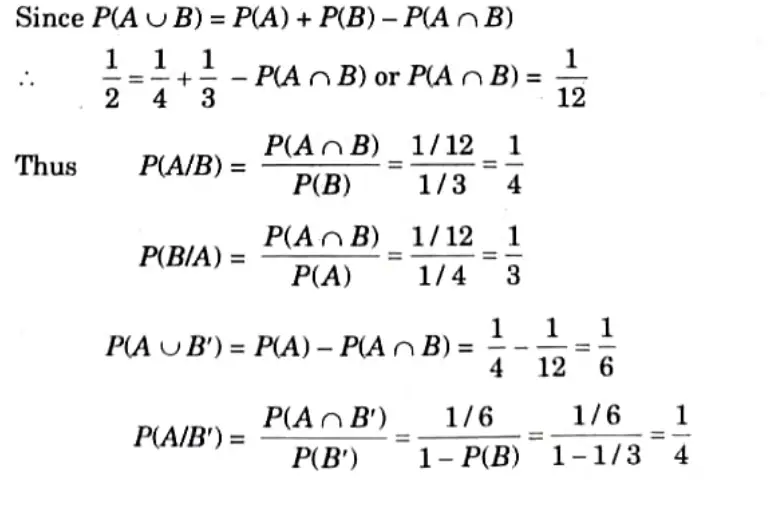
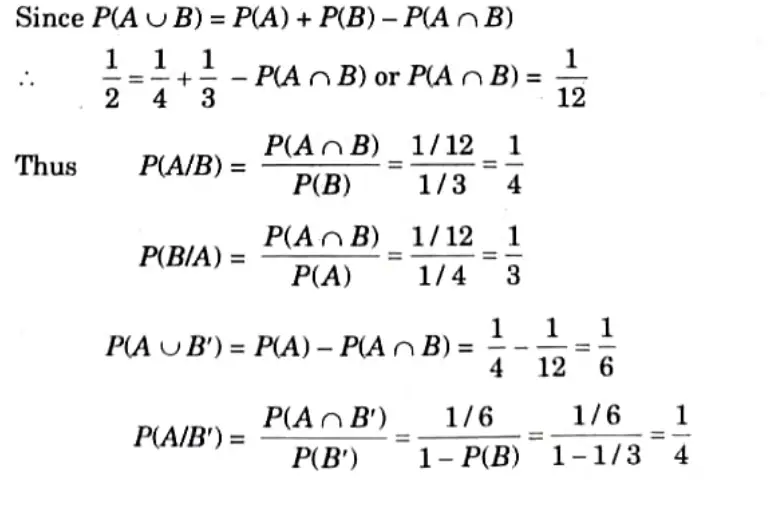
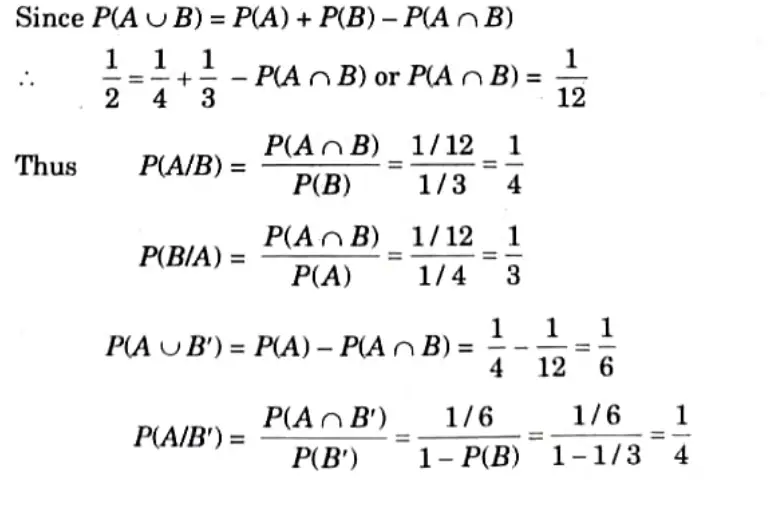
Q4. Find the chance of throwing (a) four, (b) an even number with an ordinary six faced die.
Ans.
a. There are six possible ways in which the die can fall out of which there is only one ways of getting 4.
Thus, the required chance = 1/6
b. There are six possible ways in which the die can fall out of which there are only 3 ways of getting 2, 4 or 6.
Thus, the required chance = 3/6 = ½.
Q5. A card is drawn from a well-shuffled pack of playing cards. What is the probability that it is either a spade or an ace?
Ans.
A = Event of drawing a spade
B = Event of drawing an ace
A and B are not mutually exclusive.
AB = Event of drawing the ace of spades



Q6. A problem in mechanies is given to three students A, B, C whose chances of solving it are ½, ⅓, ¼ respectively. What is the probability that the problem will be solved?
Ans:
The probabilities of A, B, C solving the problem are ½, ⅓, ¼
The probabilities of A, B, C not solving the problem are
1-½, 1-⅓, 1-¼ i.e, ½,⅔,¾.
The probability that the problem is not solved by any of them
½ * ⅔ * ¾ = ¼
Hence, the probability that the problem in solved by at least one of them
= 1-¼ = ¾.
Q7. What is the chance that a leap year selected at random will contain 53 sundays.
Ans.
A leap year consists of 366 days, so that there are 52 full weeks (and hence 52 Sundays) and two extra days. These two days can be (i) monday, tuesday (ii) tuesday, wednesday, (ii) wednesday, thursday iv) thursday, friday (v) friday, saturday (vi) saturday, sunday (vii) sunday, monday.
Out of these 7 cases, the last two are favorable and hence the required probability = 2/7.
Q8. Find the number of permutations of all the letters of the word i) Committee (ii) Engineering.
Ans.
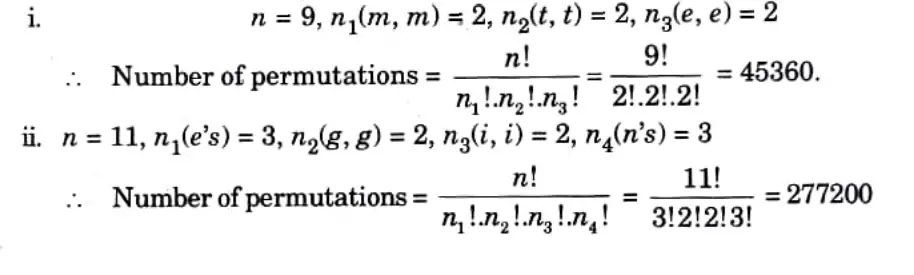
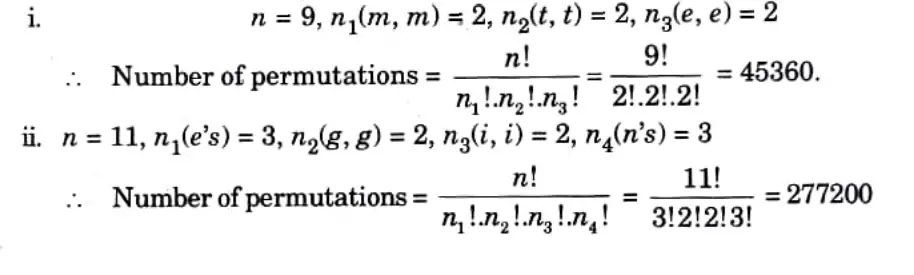
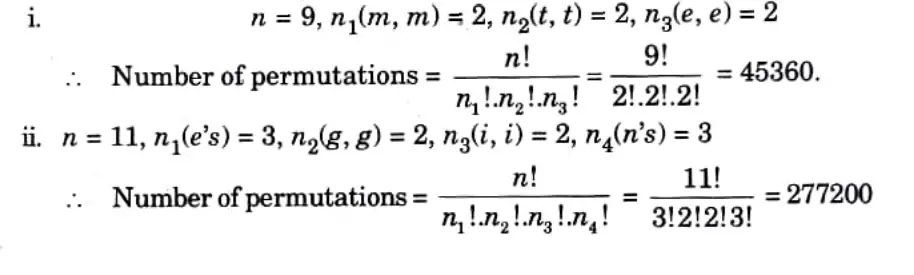
Unit-5 Statistical Techniques III
Q1. In two large populations there are 30 % and 25% respectively of fair haired people. Is this difference likely to be hidden in samples of 1200 and 900 respectively from the two populations ?
Ans.
Here
P1 = 0.3,
P2 = 0.25 So that
P1 – p2 = 0.05
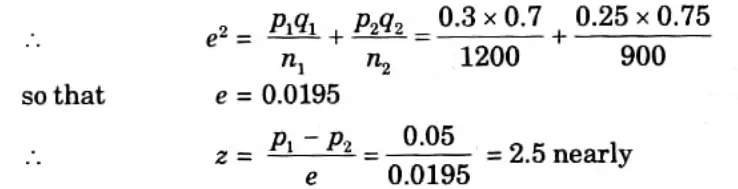
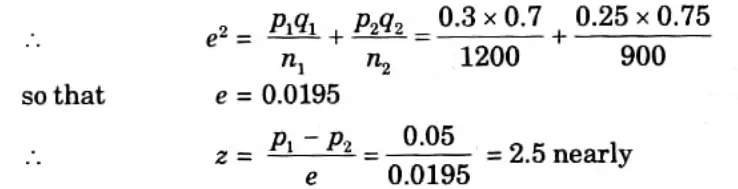
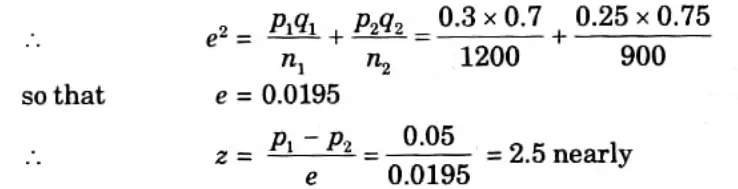
Hence, it is unlikely that the real difference will be hidden.
Q2. Explain sampling and its objectives.
Ans.
A part selected from the population is called a sample. The process of selection of a sample is called sampling. A random sample is one in which each member of the population has an equal chance of being included in it. There are C, different samples of size n that can be picked up from a population of size N.
Objective of sampling:
1. Gathering the maximum information about the population with the minimum effort, cost and time.
2. To obtain the best possible values of the parameters under specified conditions.
3. The logic of the sampling theory is the logic of induction in which we pass from a particular (sample) to the general population.
Q3. Define statistical hypothesis.
Ans.
Statistical hypothesis is an assumption on conjecture or guess about the parameters of population distribution. When more than one population is considered, the statistical hypothesis consists of the relationship between the parameter of the populations.
Q4. Define null hypothesis.
Ans. Null hypothesis denoted by H0 is the statistical hypothesis which is to be actually tested for acceptance or rejection.
Q5. What is upper control limit?
Ans. Upper Control Limit (UCL) the highest value that a quality characteristic can take before the process becomes out of control.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Math -4 Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Electronic Engineering Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
Important Links-Btech (AKTU)

1 thought on “Math-4 Important Short Question-Btech AKTU”