The Btech Math 4 previous year question paper for AKTU might assist students prepare for their examinations. It comprises questions from all sections on the curriculum and can provide students an indication of the question formats, grading, and difficulty level. Practicing these papers can help them enhance their skills and shortcomings.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Math 4 (Mathematics 4): *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Section A: Short Important Question- 2023
a. Solve the following partial differential equation (D2 + DD’) z = 0.
Ans.



b. Derive a partial differential equation by eliminating the constants a and b from z = ax + a2y2 + b.
Ans. Differentiating z partially w.r.t x and y
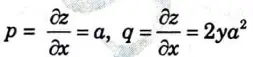
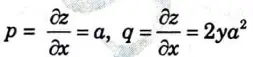
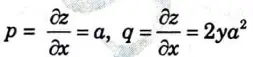
Substituting for a and b in the given equation we get
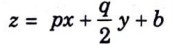
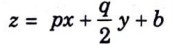
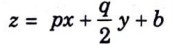
Constant b cannot be eliminated
c. Write radio wave equations.
Ans.
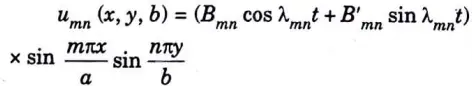
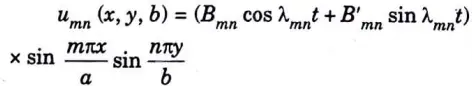
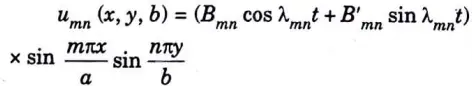
d. Classify the partial differential equation uxx + 3uxy +uyy = 0
Ans. uxx + 3uxy +uyy = 0 ……(i)
Comparing equation and with
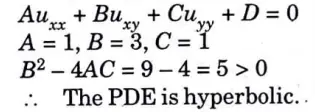
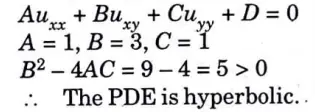
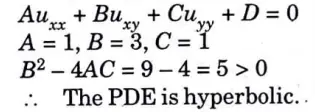
e. In an asymmetrical distribution mean is 16 and median is 20. Calculate the mode of the distribution.
Ans. Mode = 3 Median – 2 Mean
= 3 x 20 – x 16
= 60 – 32
= 28
f. The lines of regression of y on x and x on y are respectively y = x + 5 and 16x – 9y = 94. Find the correlation coefficient.
Ans. Given equation of regression lines are,



Multiply equation (i) by 9 and add equation (ii)



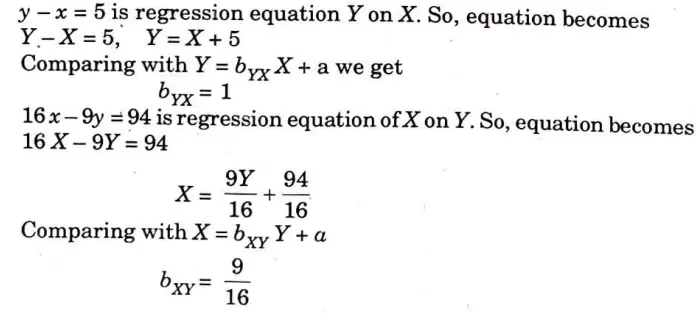
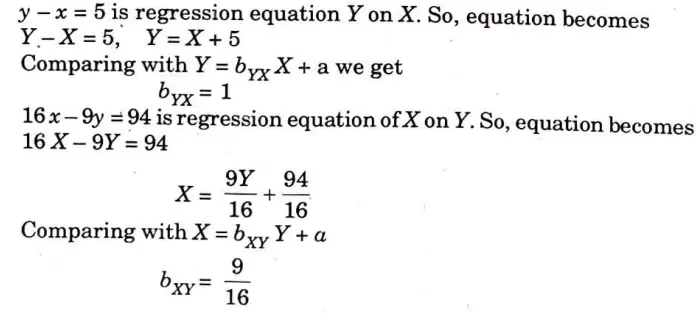
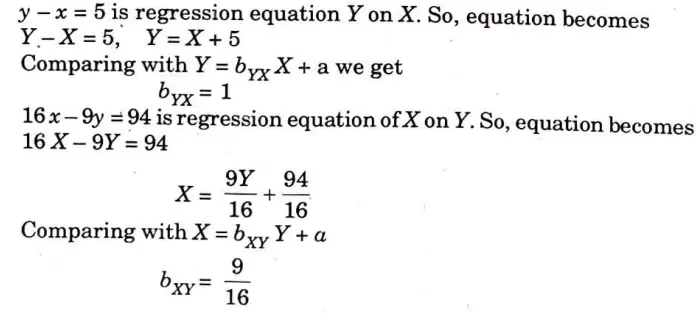
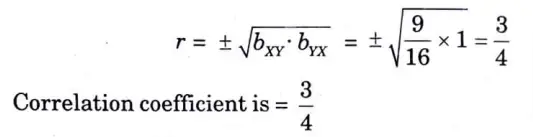
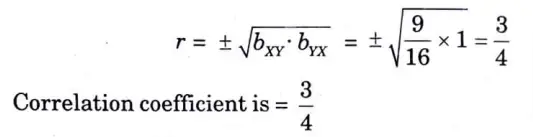
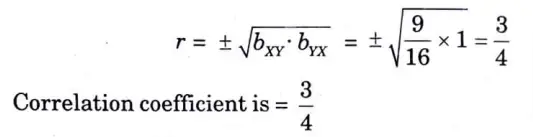
g. Four persons are chosen at random from a group containing 3 men, 2 women and 4 children. Prove that the chance that exactly two of them will be children is 10/21.
Ans. Total number of ways = 9C4 = 126 ways
There are 4 children, and we have to select exactly 2 children.
Henc, we have 4C2 ways = 6 ways.
Also, choose other two people from men and women. So we have, 5C2 ways = 10 ways.
Hence, the required probability = (6 x 10)/126 = 10/21.
h. If the probability density functions (fig A) find the value of ‘k’. Also find the probability between x = 1/2 & x=3/2.
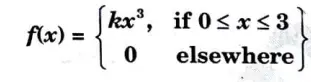
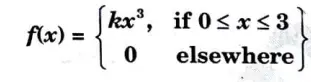
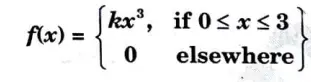
Ans.
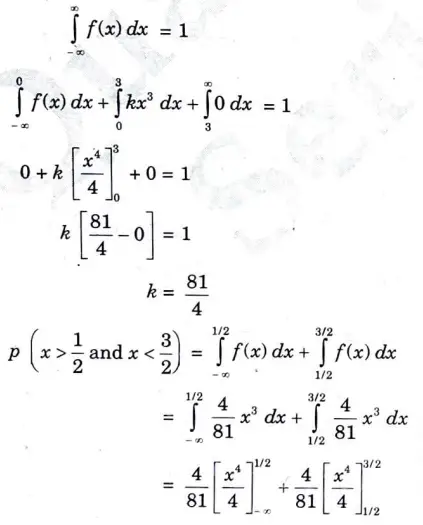
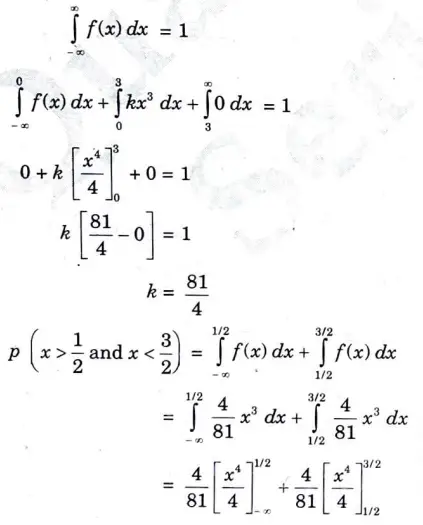
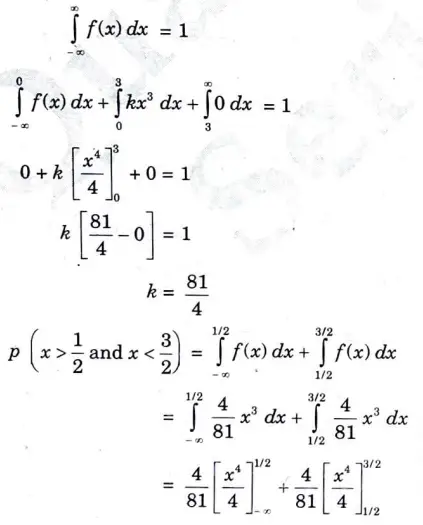
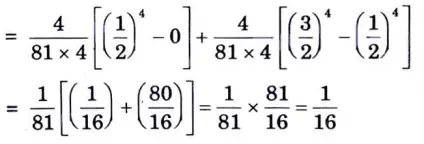
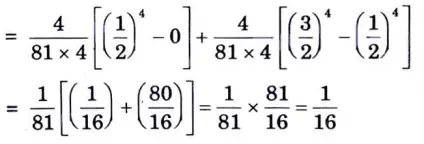
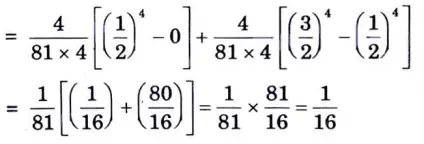
i. Explain t – test for “small samples”.
Ans. The t – distribution is used to test the significance of:
i. The mean of a small sample.
ii. The difference between the means of two small samples or to compare two samples.
iii. The correlation coefficient.
Let x1, x2,….., xn, be the members of random sample drawn from a normal population with mean μ. If X̄ be the mean of the sample then
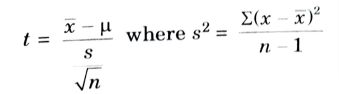
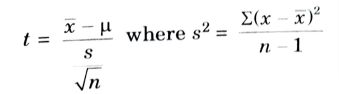
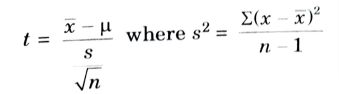
j. What do you mean by statistical quality control (SQC)?
Ans. Statistical quality control can be simply defined as an economic and effective system of maintaining and improving the quality of outputs throughout the whole operating process specification, production and inspection based on continuous testing with random samples.
Section B : Long Important Question Answer Math-4 Btech
a. Solve the partial differential equation (D – D’ -1) (D – D’ – 2) = sin (2x + 3y)
Ans.
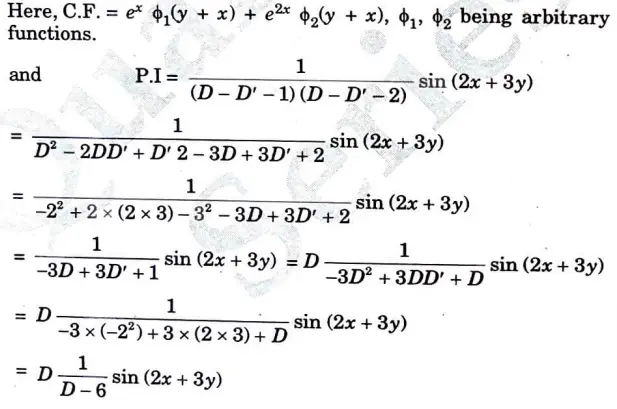
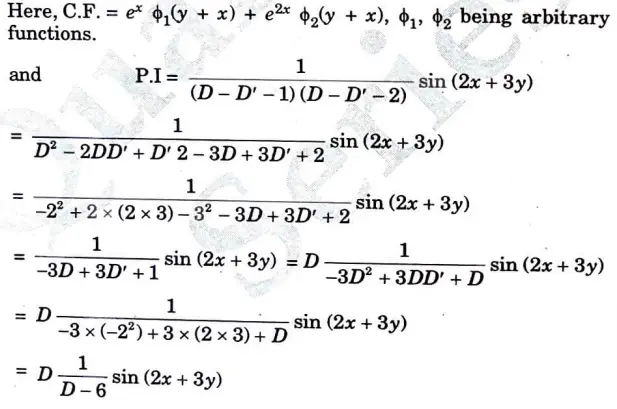
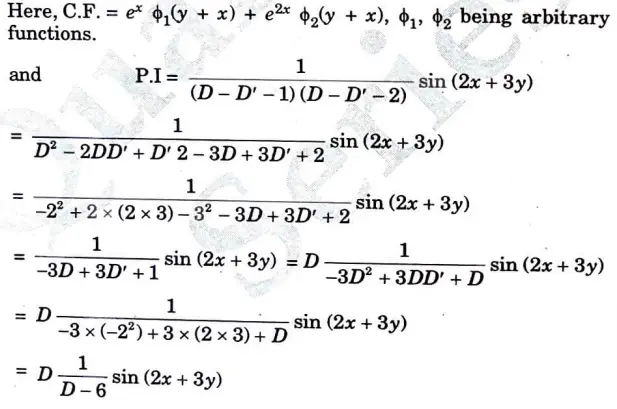
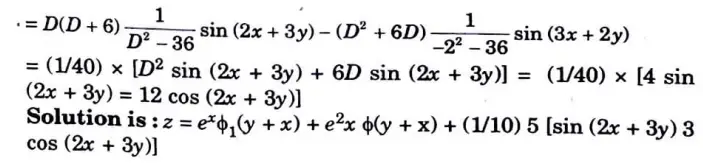
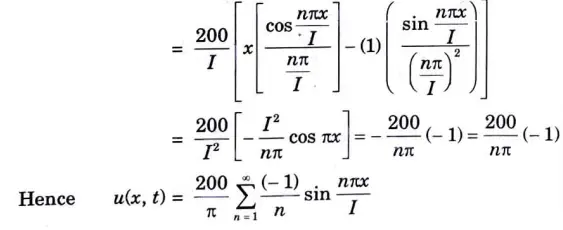
b. A laterally insulated bar of length has its ends A and B maintained at 0°C and 100°C respectively until steady state conditions prevail. If the temperature at B is suddenly reduced to 0°C and kept a while that of A is maintained at 0°C. Find the temperature at a distance x from A at any time t.
Ans. The temperature function u(x, t) satisfies the differential equation
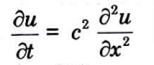
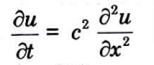
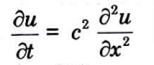
The boundary conditions associated with the problem are



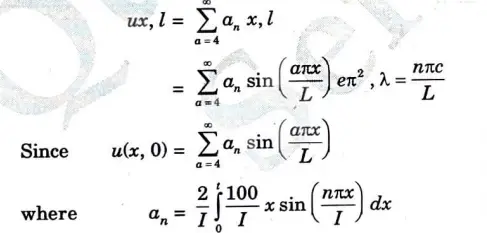
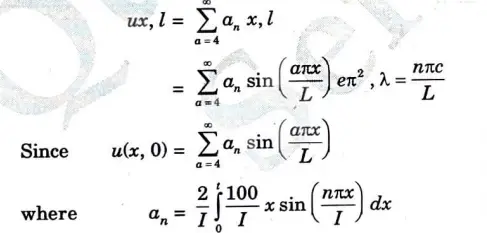
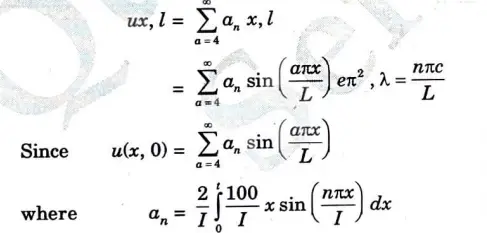


c. Calculate the first four central moments about the mean of the following data



Ans.
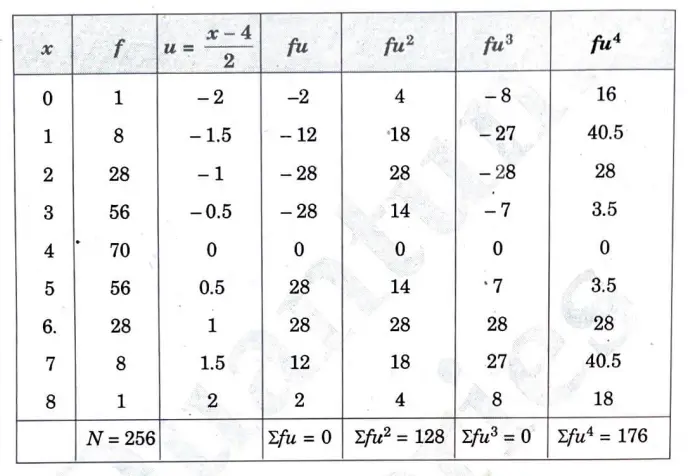


Moments about 4:



Moments about mean:
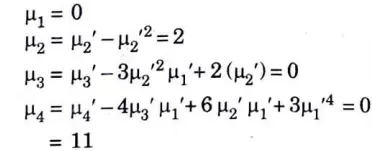
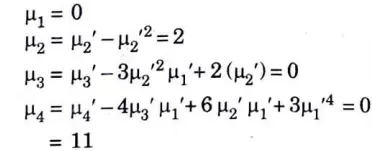
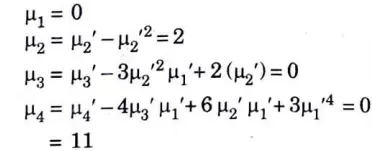
d. In a sample of 1000 cases, the mean of a certain test 14 and S.D is 2.5. Assuming the distribution to be normal, find
i. How many students score between 12 and 15?
ii. How many score above 18?
iii. How many score below 8?
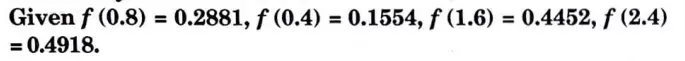
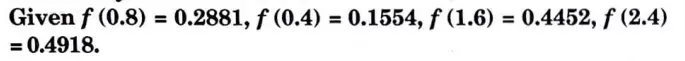
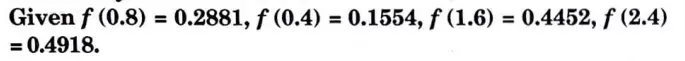
Ans.






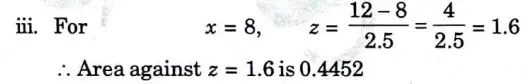
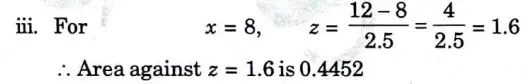
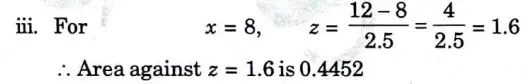



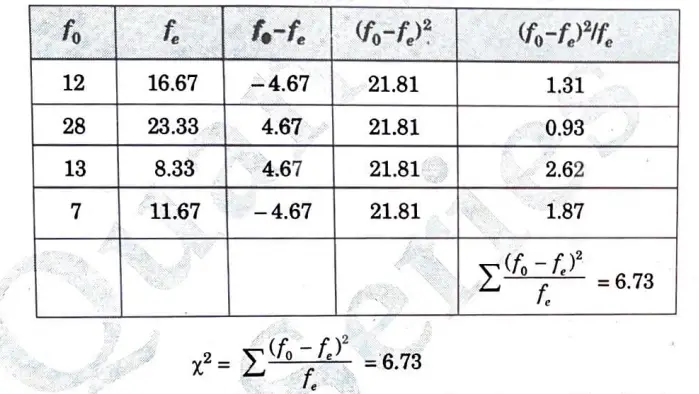
e. In an experiment on immunization of cattle from tuberculosis the following results were obtained:
| Affected | Unaffected | |
| Inoculated | 12 | 28 |
| Not inoculated | 13 | 7 |
Examine the effect of vaccine in controlling the incidence of the disease.



Ans.
| Affected | Unaffected | |
| Inoculated | 12 | 28 |
| Not inoculated | 13 | 7 |
| Total | 25 | 60 |
Let us suppose the null hypothesis is that there is no effect of vaccine in controlling the incidence of the disease.








Section 3: Long Questions Math 4 Btech AKTU
a. Solve (y + zx) p – (x + yz) q = x2 – y2
Ans. Given, (y + zx) p – (x + yz) q = x2 – y2
This equation is of the form Pp +Qq = R (Lagrange’s linear partial differential equation).
Here, P = y + xz, Q = -(x +yz), R = x2 – y2
The subsidiary equations are
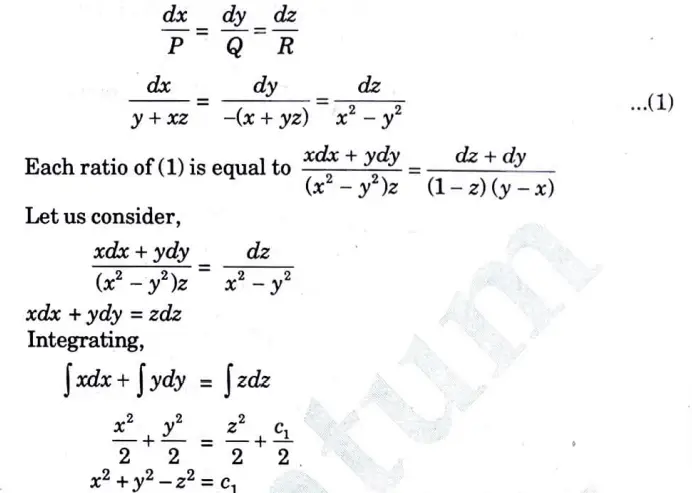
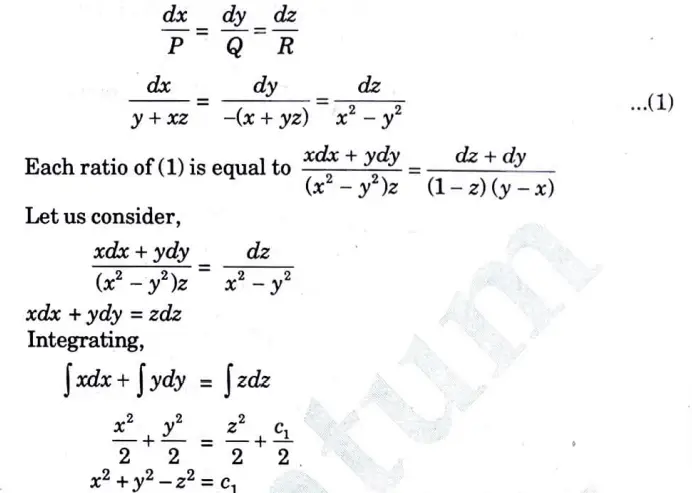
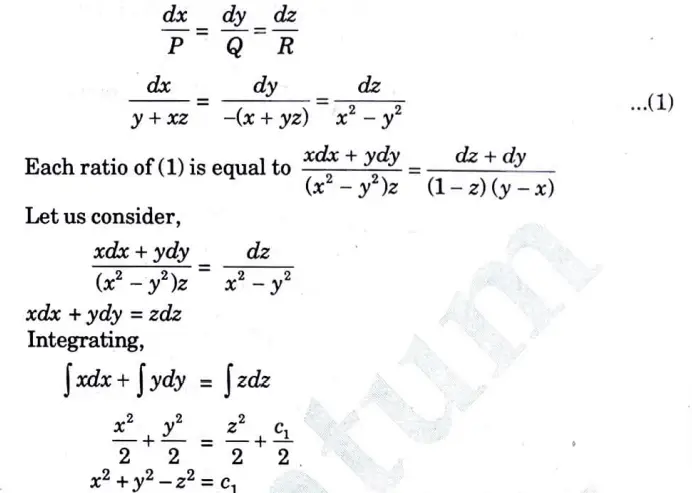
Consider
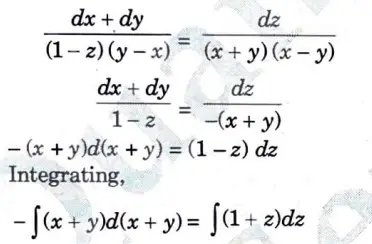
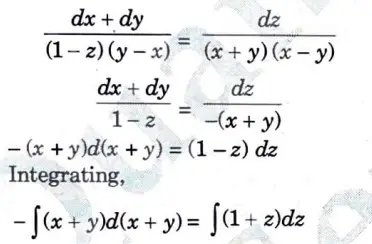
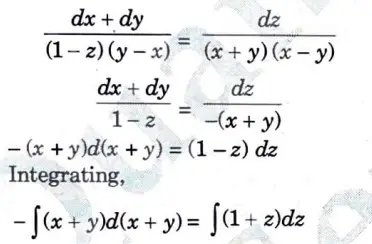
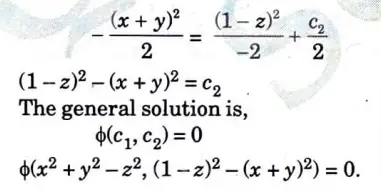
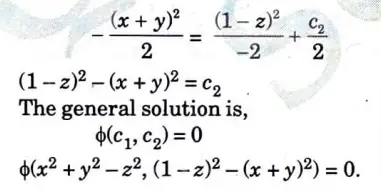
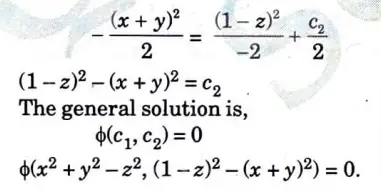
Section 4: Long Question
a. Solve the following partial differential equation by using method of separation of variables:



Ans. Applying the method of separation of variables, let z = X(x) Y(y).
Putting this with given equation, we get
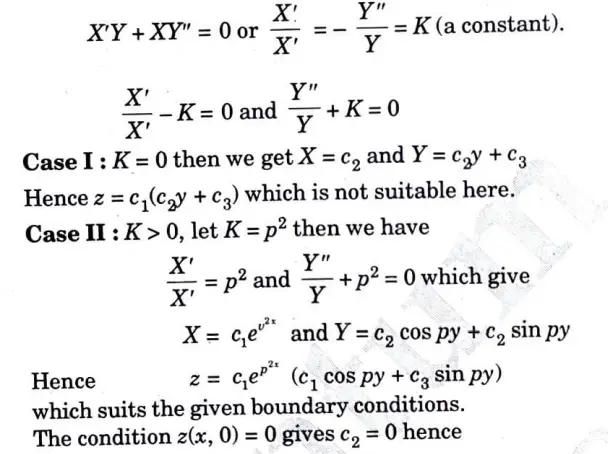
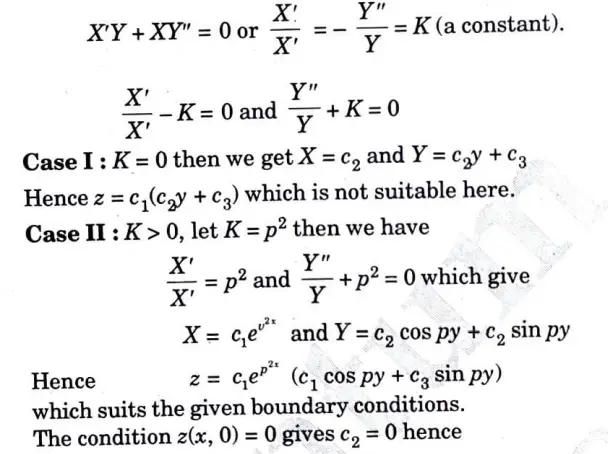
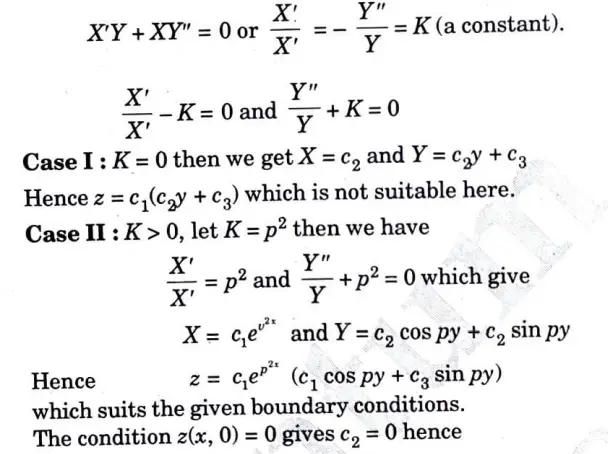
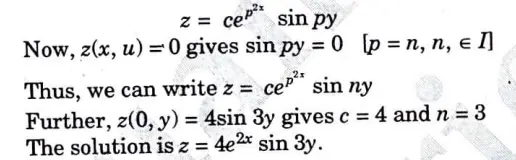
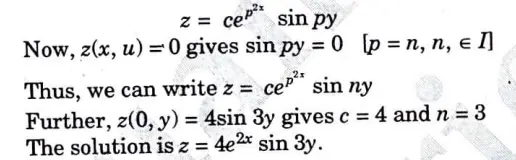
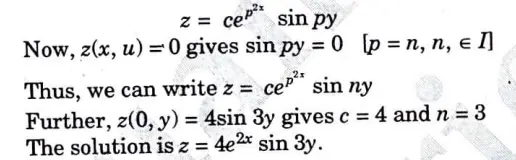
b. A string is stretched and fastened to two points/m apart. Motion is started by displacing the string in the form u(x,0) = A Sin πx/l from which it is released at time t = 0. Show that the displacement of any point at a distance x from one end at time t is given by u(x,t) = A Sin πx/l Cos πct/l
Ans. The equation of string is given by



Since, the string is displaced from the initial position at time t = 0
hence the initial displacement is given is



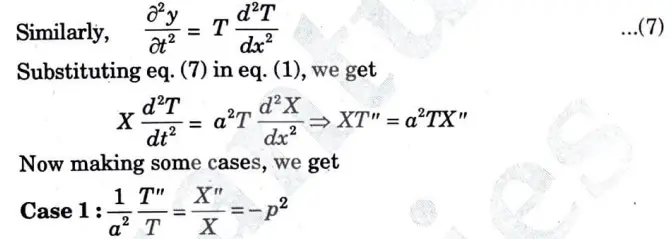
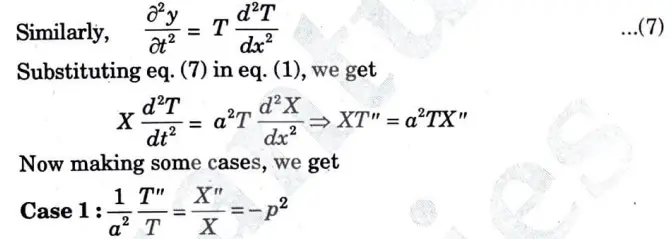
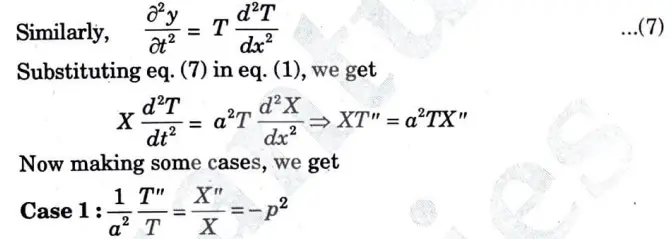



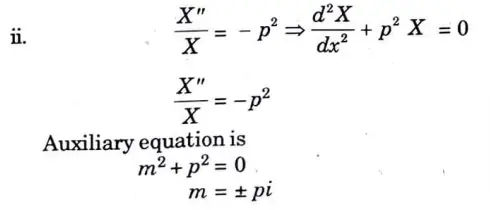
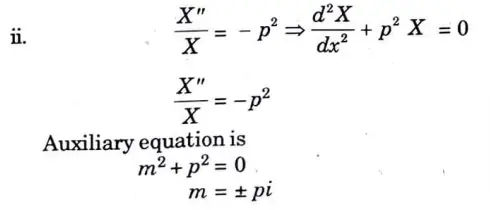
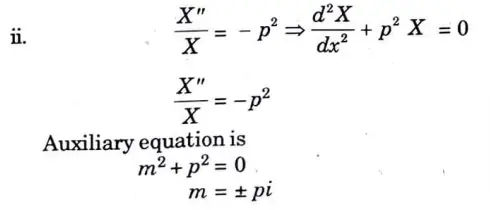






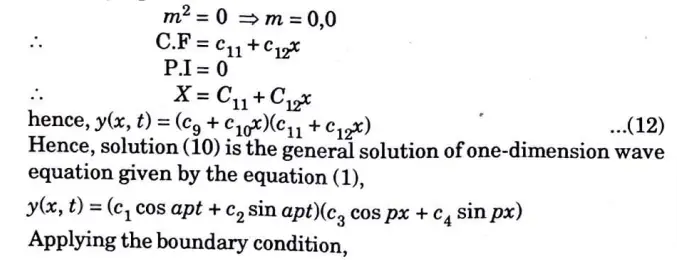
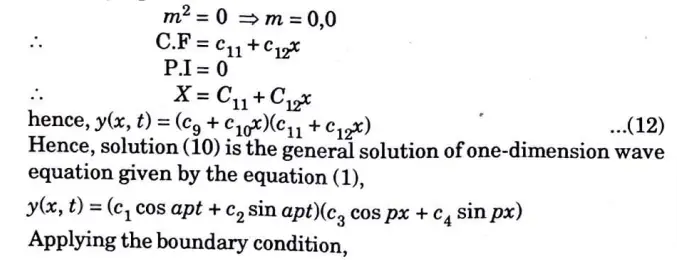
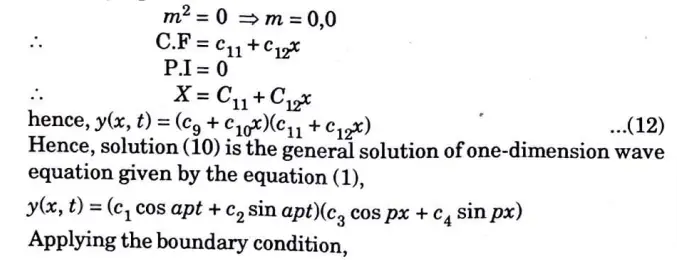
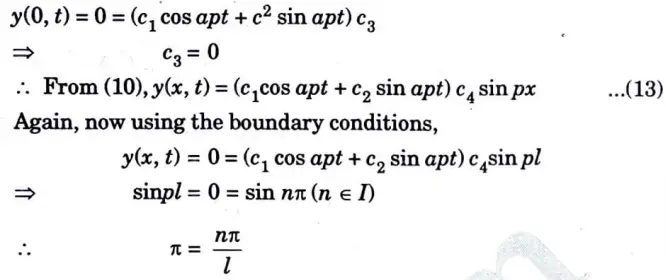
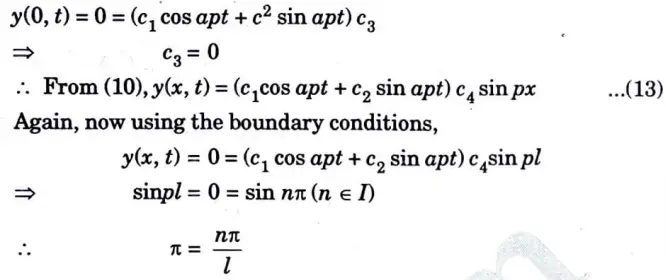
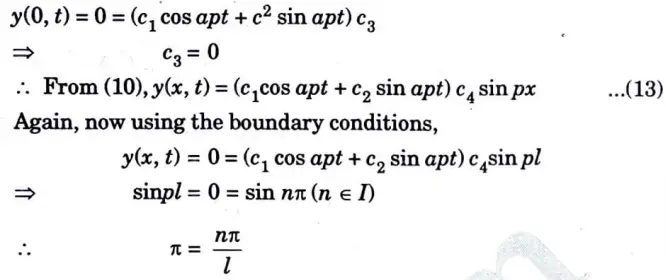



Section 5: Long Question
a. Fit a parabolic curve of regression of y on x to the following data:



Ans. We shift the origin to (2.5, 0) and take 0.5 as the new unit. This changes the variable x to X, by the relation X = 2x – 5.
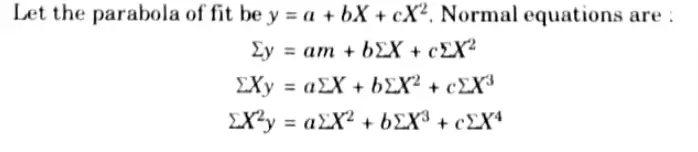
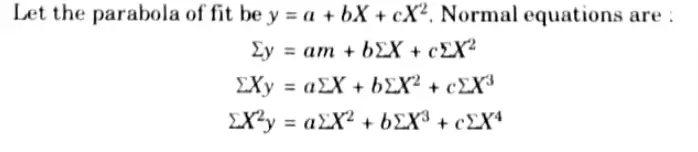
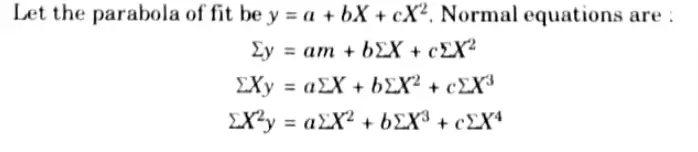
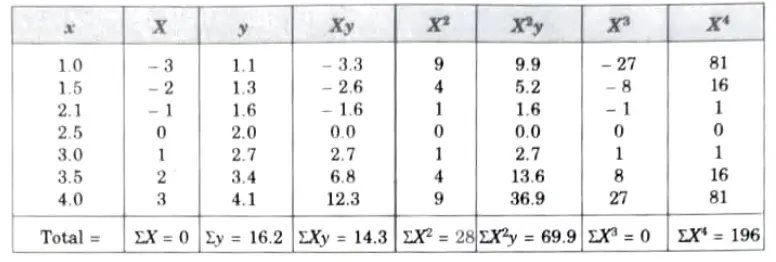


Substituting the values in normal equations, we get
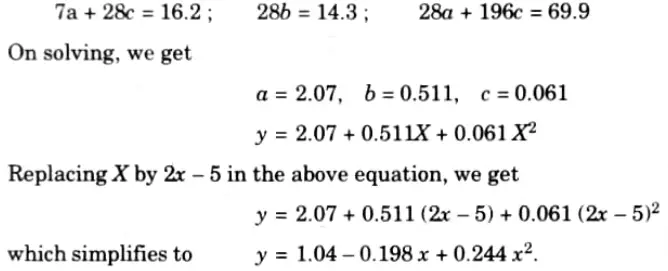
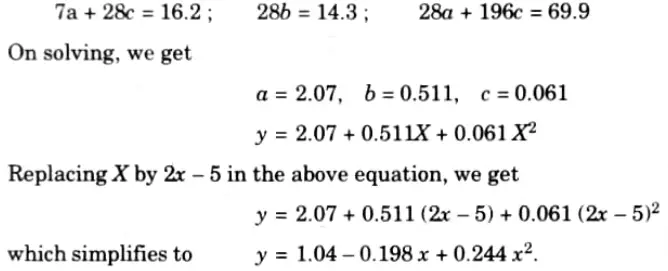
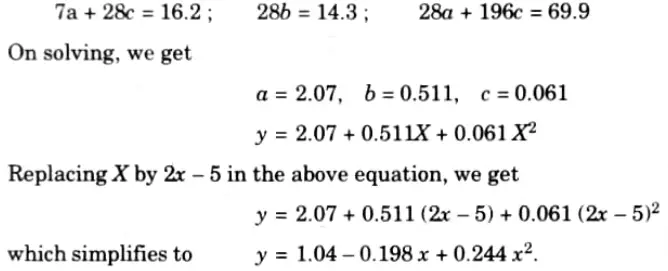
This is the required parabola of best fit.
b. Let the random variable X assume the value ‘r’ with the probability law p(X = r) = qr-1 p; r = 1,2,3 …. Find the m.g.f. of X and hence it’s mean and variance.
Ans. By the definition of m.g.f.



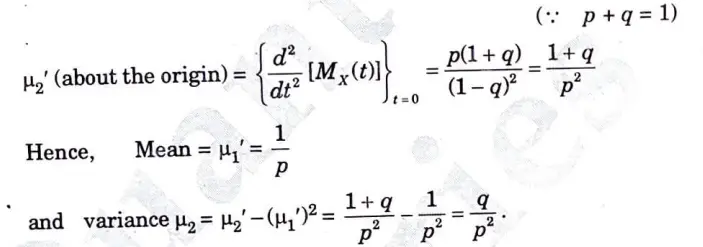
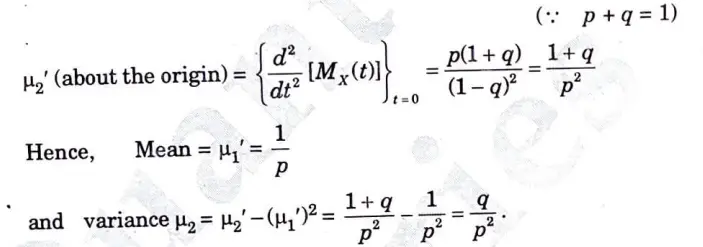
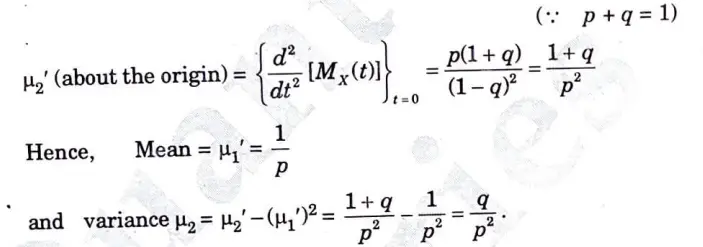
Section 6: Long Solved Question
b. The number of accidents in a year involving taxi drivers in a city follows a Poisson distribution with mean equal to 3. Out of 1000 taxi drivers, find approximately the number of drivers such that
i. No accident in a year
ii. More than three accidents in a year.
(give, e-3 = 0.04979).
Ans.
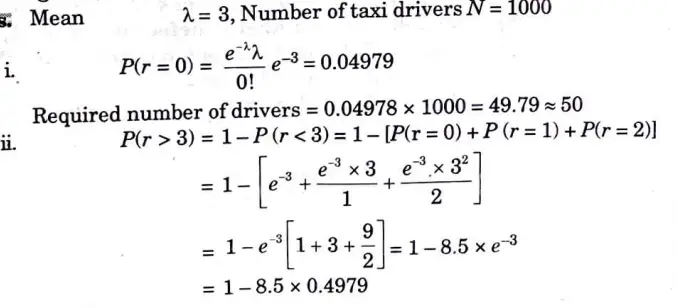
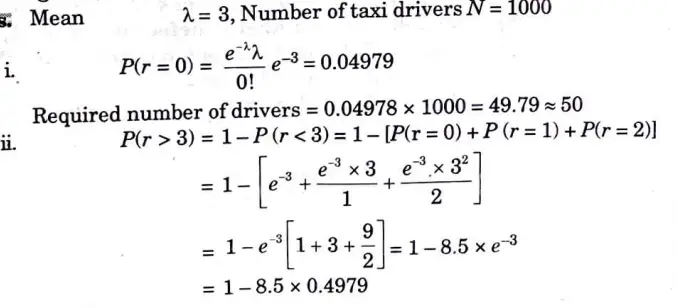
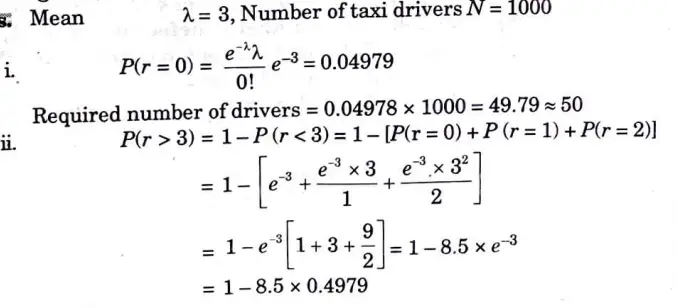
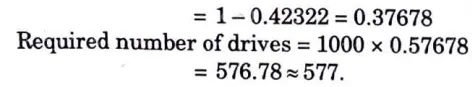
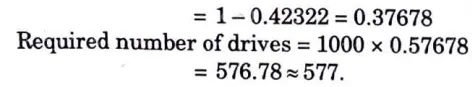
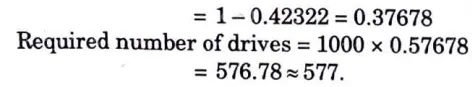
Section 7 : Long Question Answer
a. In two independent sample of size 8 and 10, the sum of square of deviations of the sample values from the respective means were 84.4 and 102.6. Test whether the difference of variances of population is segment or not. Use a 5% level of significance. [F005(7.9) = 3.29]
Ans.
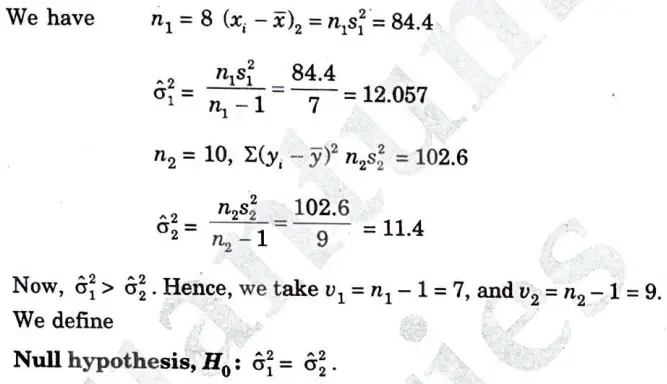
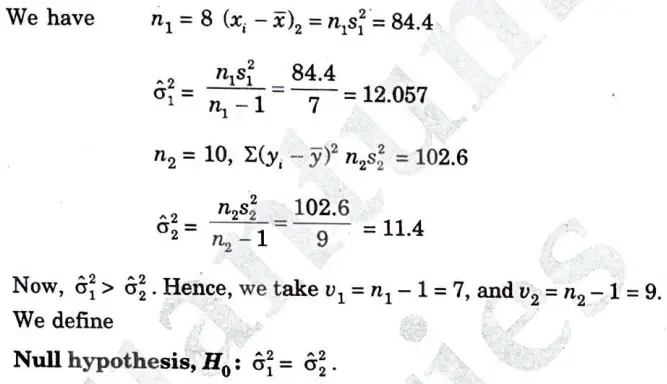
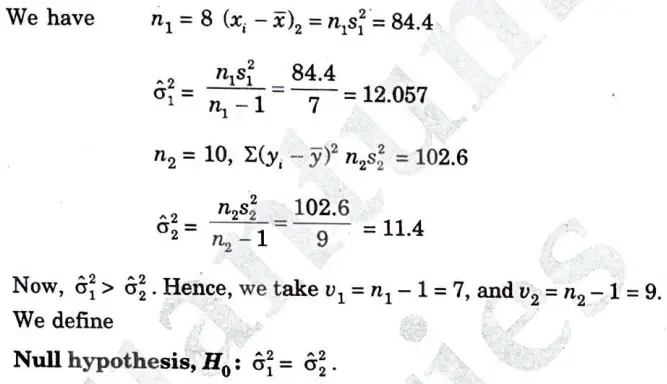
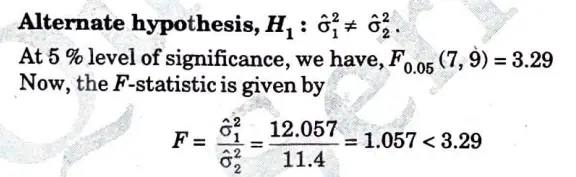
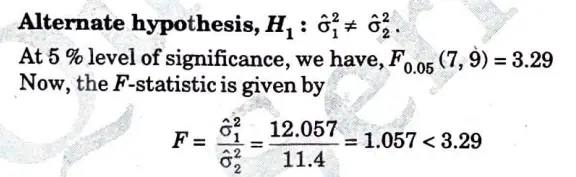
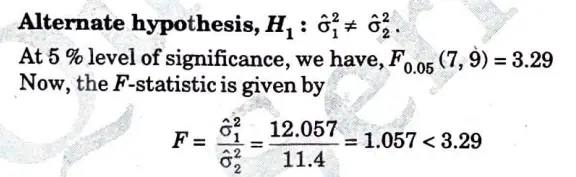
Therefore, we accept the null hypothesis. There is no significant difference between the population variance.
b. An inspection of 10 samples of size 400 each from 10 lots revealed the following number of defective units: 17, 15, 14, 26, 9, 4, 19, 12, 9, ,15. Draw the np-charts and state whether the process is under control or not.
Ans. Here, we have
Total number of items in 10 samples = N = 10 x 400 = 4000
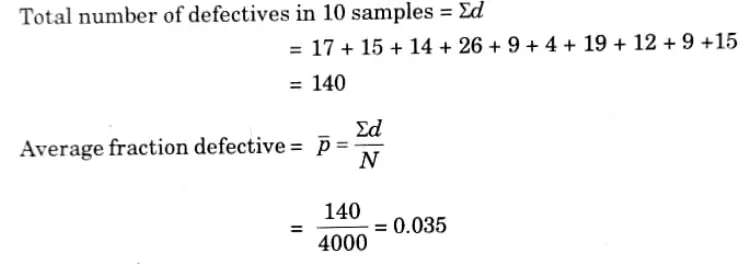
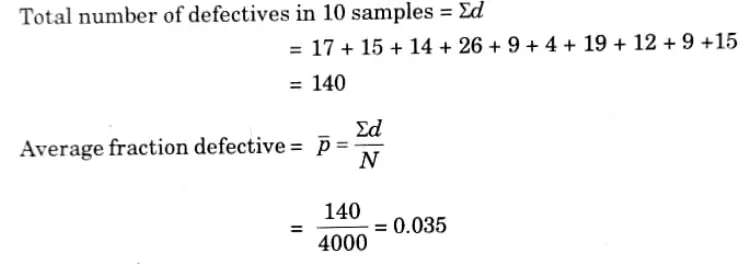
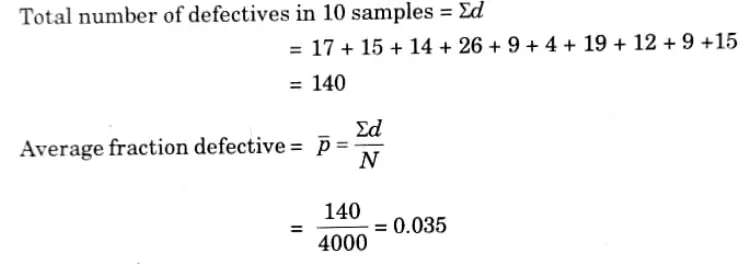
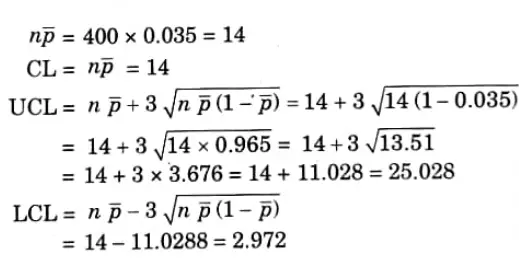
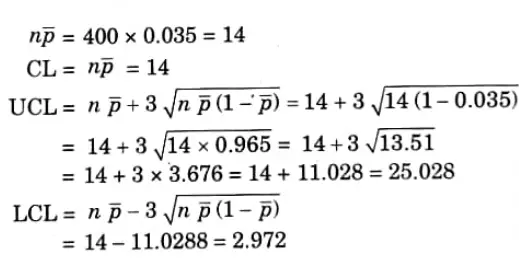
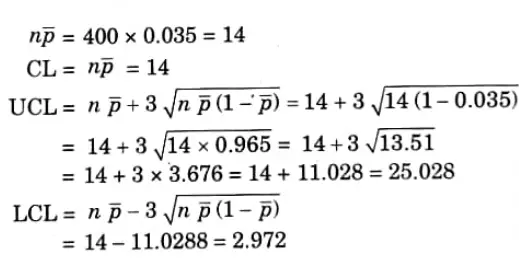
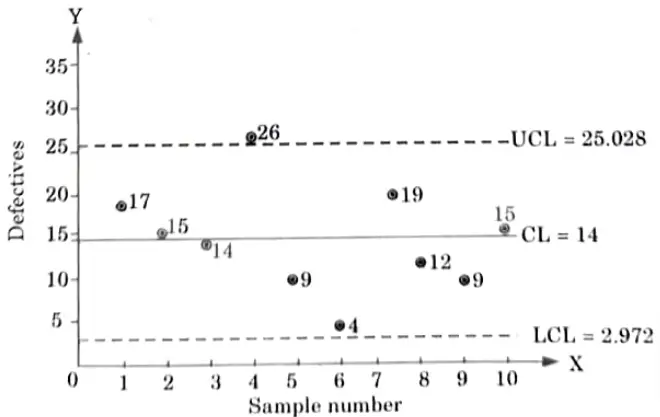


The number of defective units 26 in the 4th sample is greater than the value of the upper control limits of 25. Hence, the sample point falls outside the upper control limit, so, the process is not under control.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Math -4 Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Math 4 Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
