Students study about the kinematics of rigid bodies in Unit 05 of Engineering Mechanics for AKTU B.Tech. By studying this course, students will be able to understand and solve issues relating to the kinematics of rigid bodies, which is useful in many domains of engineering.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Engineering Mechanics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. Discuss the various types of plane motion.
Ans. Generally a body undergoes the following three types of plane motion:
i. Translation:
- 1. A straight line drawn on the moving body stays parallel to its original place at all times because the particles have the same velocity and acceleration throughout translation.
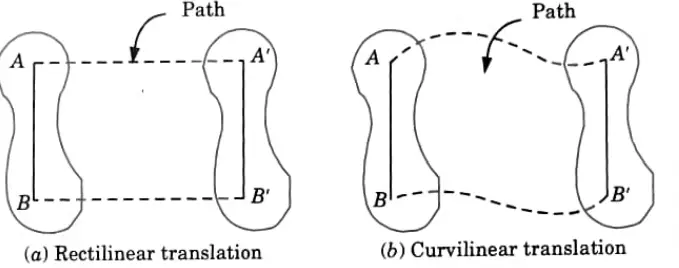


- 2. Rectilinear translation is described as a motion in which the particles follow a straight line as they move (Fig. 5.4.1). (a).
- 3. Curvilinear translation is the name for a motion in which a particle follows a curved route (Fig. 5.4.16).
ii. Rotation:
- 1.All of the particles that make up the body move in a circular motion as it rotates around a fixed point.
- 2. The fixed point that the body rotates around is known as the point of rotation, and the axis that passes through it is known as the axis of rotation.
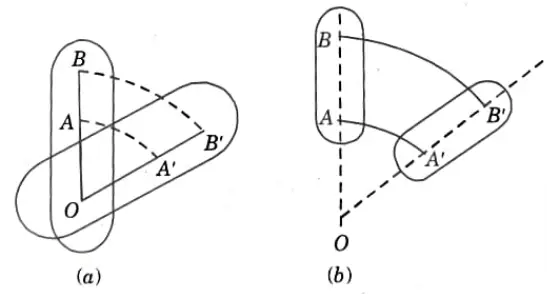


iii. General Plane Motion (Combined Motion of Translation and Rotation):
- 1. General plane motion is the term used to describe when a body exhibits both translation and rotation motions at the same time.
Example: (i) Motion of roller without slipping, motion of wheel of a locomotive train, truck and car etc.,
(ii) Arod sliding against a wall at one end and floor at the other end.
Q2. A particle of mass 1 kg moves in a straight line under the influence of a force which increases linearly with time at the rate of 60 N per sec. At time t = 0, the initial force may be taken as 50 N. Determine the acceleration and velocity of the particle 4 sec after it started from the rest at the origin.
Ans.



1. Force is increasing linearly with time. Hence applied force on the particle is a function of time.



where, A and B are constant.
2. When t = 0, F = 50 N. Now eq. (5.5.1) becomes,
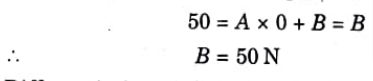
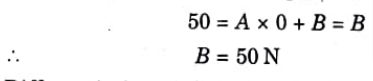
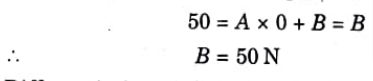
3. Differentiating eq. (5.5.1), we get
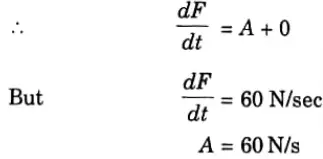
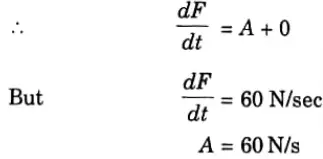
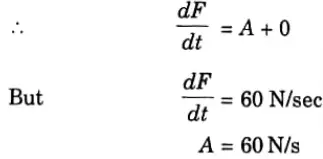
4. Substituting the value A and B in eq. (5.5.1), we get
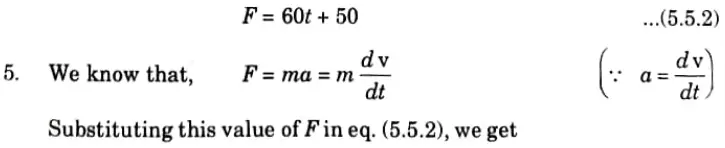
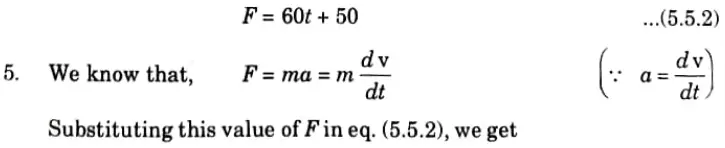
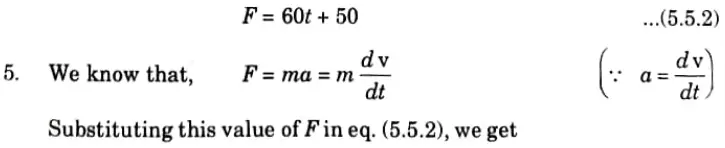



6. Integrating the eq. (5.5.4) w.r.t time, we get



7. From eq. (5.5.3), we have
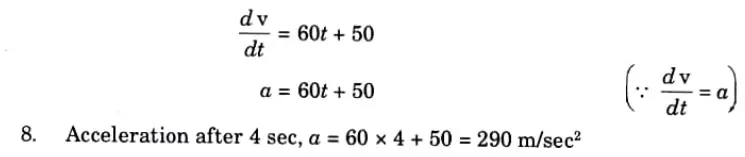
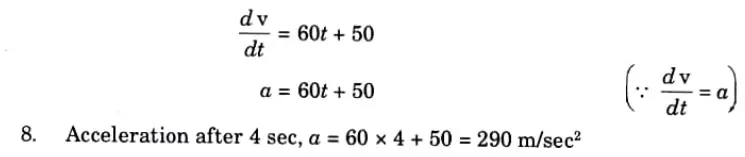
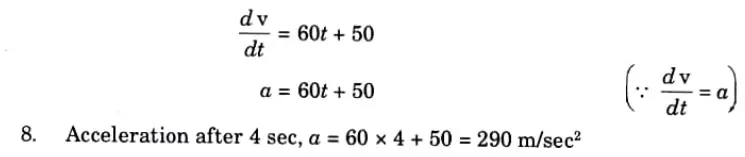
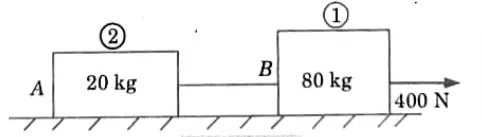
Q3. Two bodies of masses 80 kg and 20 kg are connected by a thread along a rough horizontal surface under the action of a force 400 N applied to the first body of mass 80 kg as shown in Fig. The coefficient of friction between the sliding surfaces of the bodies and plane is 0.3. Determine the acceleration of two bodies and tension in the thread using D’Alembert’s principle.


Ans.
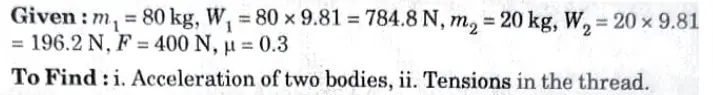
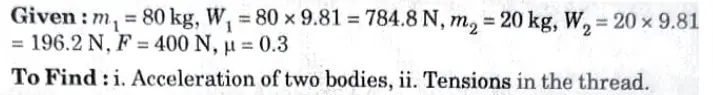
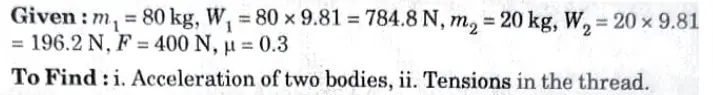
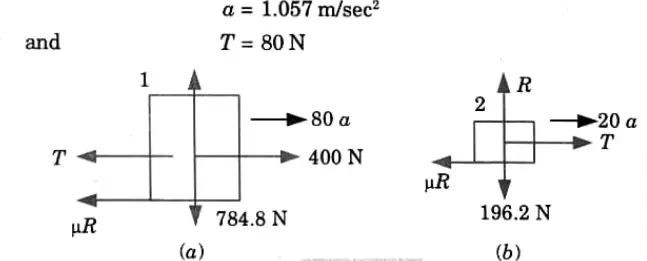
1. Let us consider, both the blocks are moving with acceleration and tension developed in thread is T.
2. Considering FBD of Block 1 (Fig. 5.10.2 (a)
Using D’Alembert’s principle,



3. Considering FBD of Block 2 (Fig. 5.10.2(b))
Using D’Alembert’s principle,



4. On solving the eq. (5.10.1) and eq. (5.10.2), we get


Q4. A system of weight connected by string passing over pulleys A and B shown in Fig. Find the acceleration of three weights. Assuming string is weightless and ideal condition for pulleys.
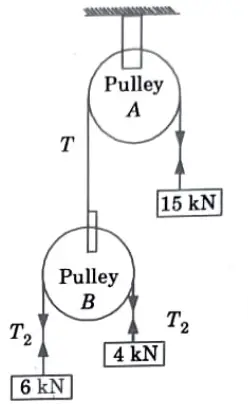


Ans. Given: Fig.
To Find: Acceleration of three weight.
1. Considering FBD for block 4 kN (Fig.)
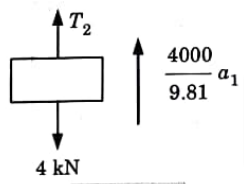





2. Considering FBD for block 6 kN (Fig.)



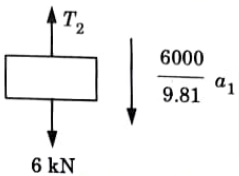





Negative sign of accelerations indicates that the direction is opposite to the direction as shown in Fig. 5.11.4.
Q5. A body of mass 30 kg is projected up an incline of 30 with an initial velocity of 10 m/sec. The friction coefficient between the contacting surfaces is 0.2. Determine distance travelled by the body before coming to rest.
Ans. Given: m= 30 kg, u =10 m/sec, v = 0 rest), μ = 0.2
To Find: Distance travelled by the body before coming to rest.
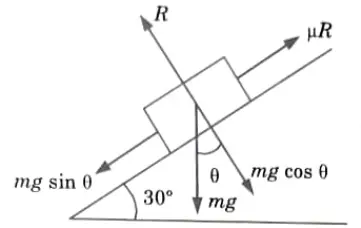


1. Resultant force acting on the block,
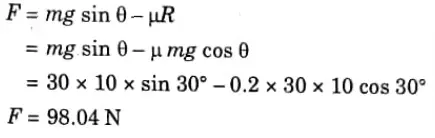
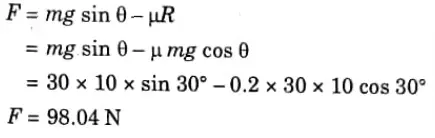
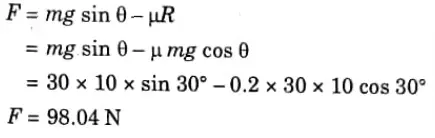
2. Using the work-energy balance equation,
Work done by the block = Kinetic energy of the block
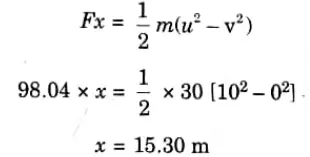
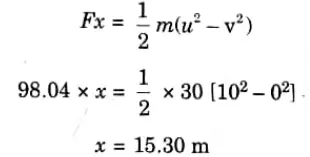
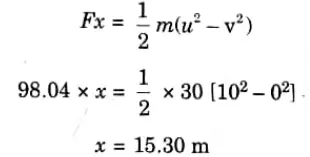
Q6. Discuss in short about work done on a particle and work done on a rigid body.
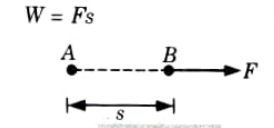
Ans. i. Work Done on a Particle:
1. A force that acts on a particle that is free to move results in the displacement of the particle. The force is said to have worked on the particle at that point.
2. Then, we define work done on the particle as the sum of the force’s magnitude and the particle’s displacement. Mathematically, we can write this as


ii. Work Done on a Rigid Body:
1. We are aware that inflexible bodies experience moments in addition to forces. Moments produce angular displacements in a manner similar to how forces produce linear displacements.
2. If a moment M acting on a rigid body causes an angular displacement then work done by the moment on the rigid body is defined as the product of moment and angular displacement, i.e.
W = Mθ,



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Engineering Mechanics Quantum, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Engineering Mechanics Quantum PDF: | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
