Here we are discussing for Important short question in AKTU Btech Engineering Mechanics.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Engineering Mechanics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Unit – 1 (Introduction to Engineering Mechanics)
Q1. What do you understand by a particle and a rigid body?
Ans. Particle: A particle is a body with an infinitely small volume, and it is thought to have its mass concentrated at a single location.
Rigid Body: A hard body is one that does not deform when subjected to external forces.
Q2. Give the effect of force and moment on a body.
Ans. While a moment produces an angular displacement, a force acting on a body produces a linear displacement.
Q3. What are the steps in making of a free body diagram?
Ans. The steps in making a free body diagram are as follows:
- i. By removing the supporting surfaces, a drawing of the body is created.
- ii. Include on this diagram all active or applied forces that tend to move the body, such as those brought on by the body’s weight or external forces, etc.
- iii. Include all reactive forces, such as those brought on by restrictions or supports that tend to inhibit motion, in this diagram as well.
- iv. The sketch displays all necessary distances, angles, and reference axes.
Q4. Define resultant of forces.
Ans. The resultant of forces is a single force that can replace many forces operating on a body and have the same consequence.
Q5. The resultant of two forces 3P and 2P is R. If the first force is doubled the resultant is also doubled, determine the angle between the two forces.
Ans. Given: P=3P,Q= 2P, P = 6P,R’= 2R
To Find: Angle between the two forces, 𝛉.
1. From parallelogram law of forces,
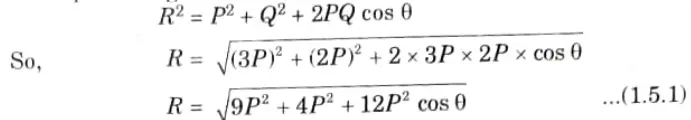
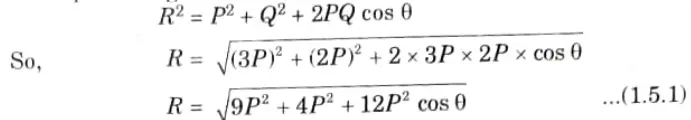
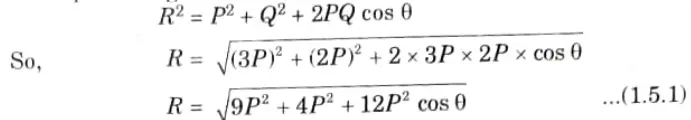
2. Now according to changed values,
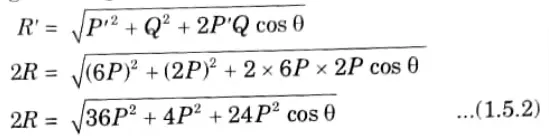
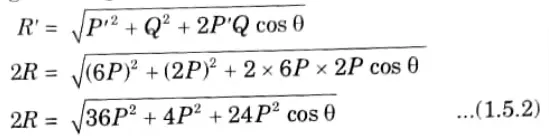
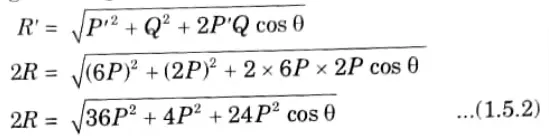
3. From eq. (1.5.1) and eq. (1.5.2), we have
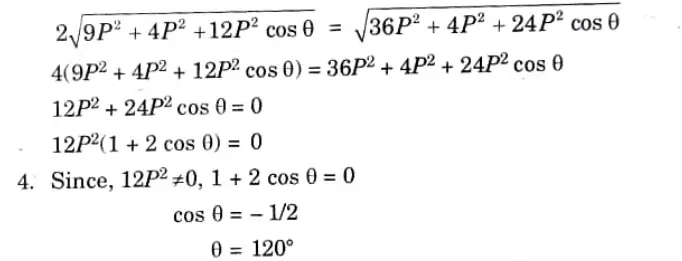
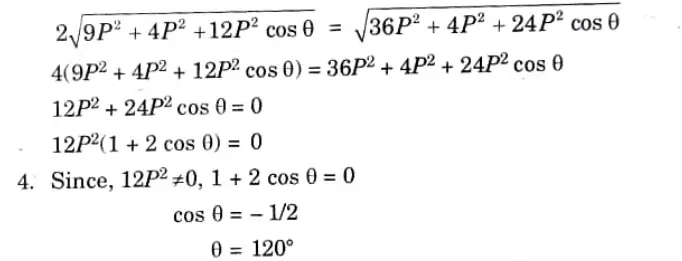
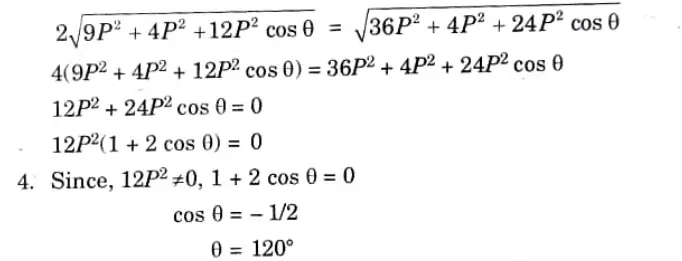
Q6. What is static equilibrium? Write down sufficient condition of static equilibrium for a coplanar concurrent and non-concurrent force system.
OR
Explain condition of equilibrium of coplanar-non concurrent forces.
Ans. Static Equilibrium: If all of the forces operating on a body, whether it is at rest or in motion, are in balance, the body is said to be in static equilibrium.
Conditions of Static Equilibrium for a Coplanar Concurrent Force System:
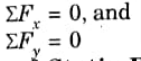
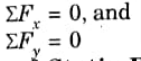
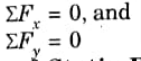
Conditions of Static Equilibrium for a Coplanar Non Concurrent Force System:
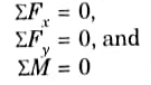
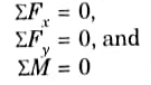
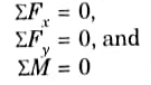
Q7. How do you find the resultant of non-coplanar concurrent force system?
Ans. By adding the components of the forces acting in the X, Y, and Z axes, one may force analytically determine the resultant of multiple forces acting in a non-coplanar concurrent system, i.e., resultant R can be obtained by,
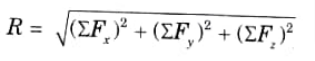
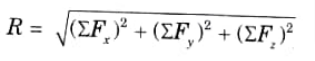
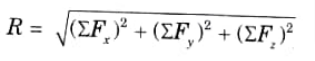
Q8. “Friction is both desirable and undesirable”. Explain
Ans. Friction facilitates the operation of friction brakes and clutches, belt and rope drives, holding and fastening mechanisms, but it can also impair the performance of power screws, bearings, and gears, as well as the flow of fluid via pipes. Thus, friction can be characterised as both desirable and undesired.
Q9. Explain the relationship between angle of friction and angle of repose.
Ans. Angle of friction = Angle of repose
Q10. A block of mass m on an inclined plane is kept in equilibrium and prevented from sliding down by applying a force of 500 N. If the angle of the inclination is 30° and coefficient of friction for the contact surface is 0.35, determine the weight of the block.
Ans. Given: F=500 N, 0= 30°, μ = 0.35
To Find: Weight of block.
1. Fig. shows the block resting on inclined plane
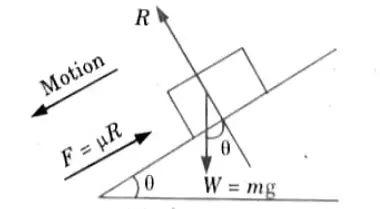


2. FBD of block is as shown in Fig.
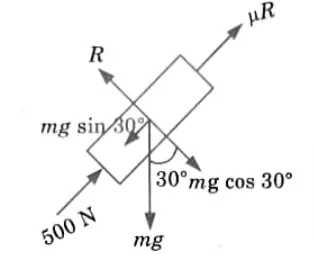


3. Equation of equilibrium along plane,
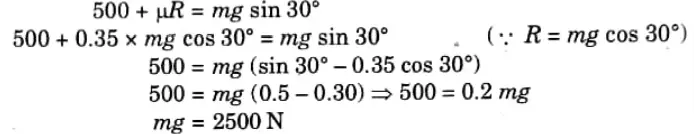
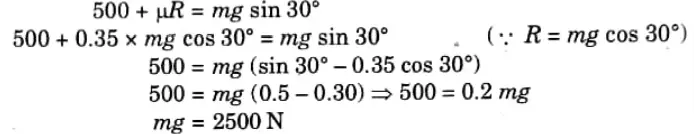
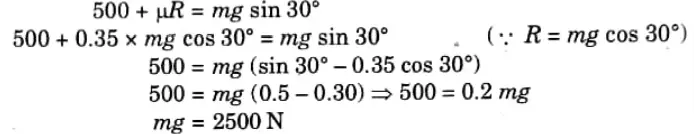
Q11. Write any four engineering applications of friction.
Ans. Following are the engineering applications of friction :
- i. In producing relative motion between bodies.
- ii. In transmitting power.
- iii. In braking system to stop the vehicle.
- iv. In lifting the heavy blocks, machinery etc., over wedges.
Q12. State Varignon’s theorem of moments.
Ans. According to Varignon’s theorem of moments, the moment of a system of coplanar forces about the same moment centre is equal to the algebraic sum of those forces’ individual moments.
Q13. Define the principle of transmissibility.
Ans. According to the principle of transmissibility, if a force operating on a rigid body is replaced by another force of the same magnitude and direction acting anywhere on the body along the line of action of the replaced force, the state of rest or motion of the rigid body remains unaffected.
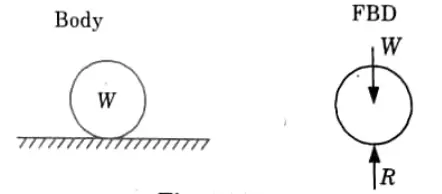
Q14. Explain free body diagram with example.
Ans. Free Body Diagram: A body can have multiple components and supports. By correctly considering the effect of forces, any element or support can be isolated from the rest of the system. Free body diagrams show the isolated element or part of the body along with the net influence of forces (FBD).
Example :


Q15. Define parallelogram law of forces.Ans. According to the parallelogram law of forces, if two forces acting simultaneously on a body at a point are represented by two adjacent sides of a parallelogram in magnitude and direction, their resultant will be represented in magnitude and direction by the parallelogram’s diagonal that passes through the point of intersection of the two sides representing the forces.
Unit – 2 Centroid and Centre of Gravity | Important Notes
Q1. What is the difference between centroid and centre of gravity?
Ans. While centroid refers to lines, planes, areas, and volumes, the phrase centre of gravity is used to describe weighted bodies.
Q2. Define axis of symmetry.
Ans. The axis of symmetry is the point at which the figure can be divided into equal halves.
Q3. Determine the centroid of a circular are having radius 20 mm and central angle 180°.
Ans.



Q4. What is the centroid of segment of a circular disc of radius 5 cm and subtended angle of 120?
Ans.
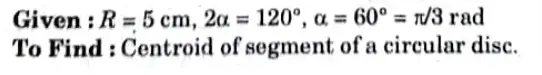
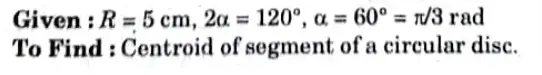
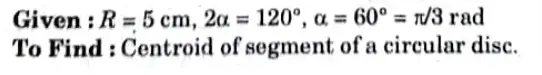
1. Centroid of circular lamina is given as,
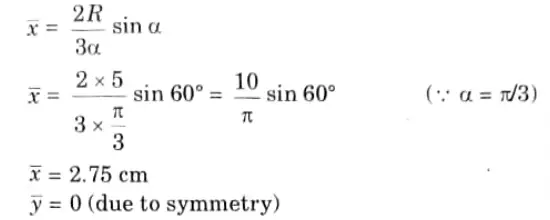
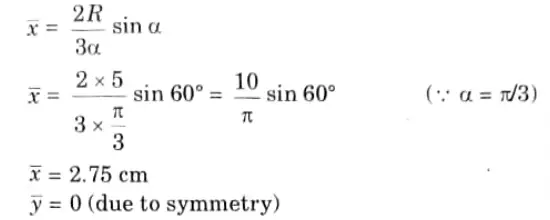
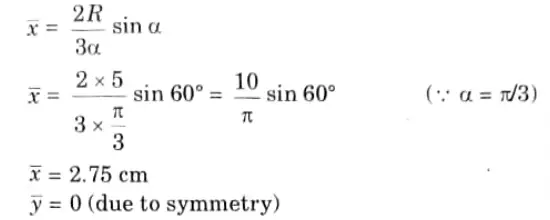
Q5. Explain polar moment of inertia.
Ans. The polar moment of inertia is the moment of inertia about an axis perpendicular to the plane of an area.
Q6. Find the polar moment of inertia of a circular area of diameter 5 mm.
Ans. Given: D = 5 mm
To Find: Polar moment of inertia
1. Polar moment of inertia of a circular disc is given as,
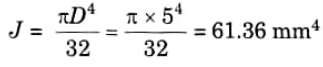
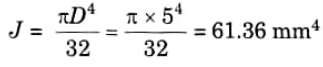
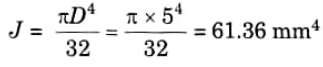
Q7. What do you understand by radius of gyration?
Ans. The radius of gyration is the length, which, when multiplied by the area and squared, produces the area’s moment of inertia.
Q8. State perpendicular axis theorem.
OR
State and explain perpendicular axis theorem.
Ans. According to the perpendicular axis theorem, the sum of the moments of inertia about any two mutually perpendicular axes passing through the same point O and lying in the plane of the area is equal to the moment of inertia of an area about an axis perpendicular to its plane (polar moment of inertia).Mathematically, IZZ = IXX+IYY
Q9. State parallel axis theorem.
Ans. According to the parallel axis theorem, the moment of inertia around any axis in the plane of an area is equal to the product of the area’s product and the square of the distance between the two parallel axes, as well as the moment of inertia about a parallel centroidal axis.
Q10. Define mass moment of inertia. Ans. A body’s mass moment of inertia around an axis is calculated as the sum of the products of the masses of its constituent parts multiplied by the square of their distance from the axis.
Unit – 3 Basic Structural Analysis Important Notes
Q1. Write the different types of support.
Ans. Following are the different types of support:
- i. Simple support or knife edge support,
- ii. Roller support,
- iii. Pin joint or hinged support,
- iv. Smooth surface support, and
- v. Fixed or built-in support.
Q2. List the various types of loads to which the beam can be subjected.
Ans. Following are the different types of loads to which the beam can be subjected:
- i. Concentrated or point load,
- ii Uniformly distributed load (UDL), and
- iii. Uniformly varying load (UVL).
Q3. Differentiate between perfect and imperfect truss.
Ans.
| S. No. | Perfect Truss | Imperfect Truss |
| 1. | Perfect trusses never lose their form. | When loaded, flawed trusses cannot maintain their shape and distort. |
| 2. | (2j-3) is the number of members in a perfect truss, where j is the number of joints. | There are either more or fewer members than 2j – 3. |
Q4. What do you understand by point of contraflexure?
Ans. The part of the beam where the bending moment is zero or changes its sign is represented by the point of contraflexure.
Q5. A truss structure is made up of five members. If the number of joints in the truss is four then state the nature of truss.
Ans. Given: m = 5, j = 4
To Find: Nature of truss
1. Nature of truss can be determine by the following formula,
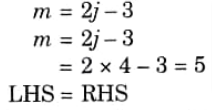
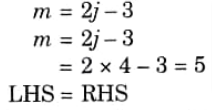
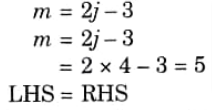
So, the given truss is a perfect truss.
Q6. What are the different methods of analyzing a frame?
Ans. A frame is analyzed by the following methods :
- i. Method of joints,
- ii. Method of section, and
- iii. Graphical method.
Q7. What assumptions are made while determining stresses in a truss ?
Ans. Following are the àssumptions made while determining stresses in a truss:
- i. The frame should be a perfect frame.
- ii. The frame carries load at the joints.
- iii. All the members are pin-joined.
Q8. Discuss the conditions under which the method of section is preferred over method of joints in analysis of truss.
Ans. The method of sections is chosen above the method of joints in the following two circumstances:
i. When applying forces to a big truss, just a few members are needed.
ii. In the event that the joints technique fails, analysis should begin or continue.
Q9. Define zero force members.
Ans. Zero force members are those truss members whose net force is zero.
Q10. With neat sketches describe in brief different types of beams.
Ans. Following are the different types of beams:
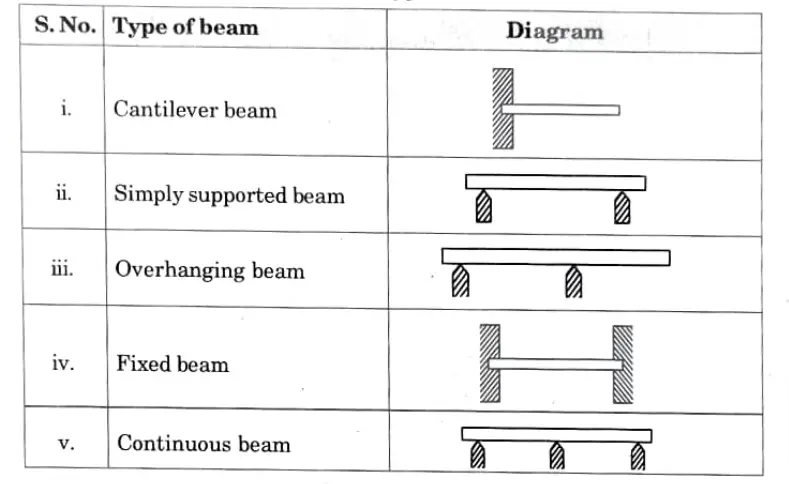


Q11. Determine the maximum bending moment in a simply supported beam having span of 5m and carrying aa uniformly distributed load of 10 kN/m throughout its span.
Ans. Given: l=5 m, w 10x 103 kN/m
To Find: Maximum bending moment.
1. We know maximum bending moment for simply supported beam carrying uniformly distributed load is given as,
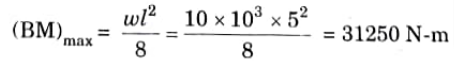
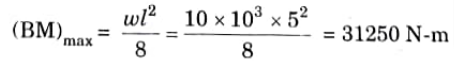
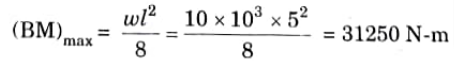
Q12. Determine the maximum bending moment in a simply supported beam of span 5 m, carrying uniformly distributed load of 2 kN/m over its entire span.
Ans. Given: w = 2 kN/m, l = 5 m
To Find: Maximum bending moment.
1. Maximum bending moment for a simply supported beam carrying uniformly distributed load is given by as,
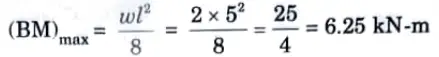
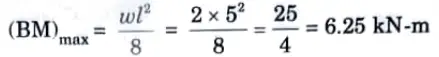
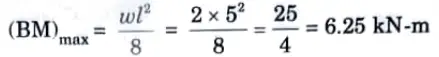
Unit – 4 Review of Particle Dynamics Important Notes
Q1. Define rectilinear motion.
Ans. Rectilinear motion is the term for a body’s motion in a straight line.
Q2. A mass of 3 kg is dropped from a height from rest. Find the distance travelled in 5 seconds.
Ans. Given: Mass 3 kg, t = 5 sec,
To Find: Distance travelled in 5 sec.
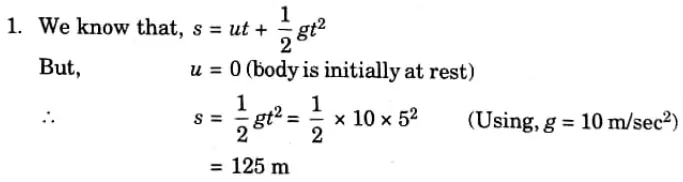
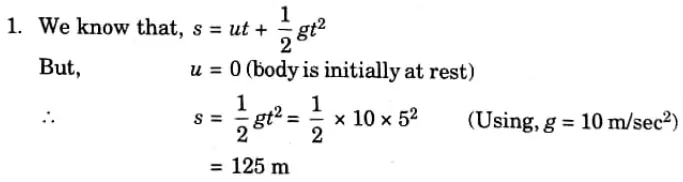
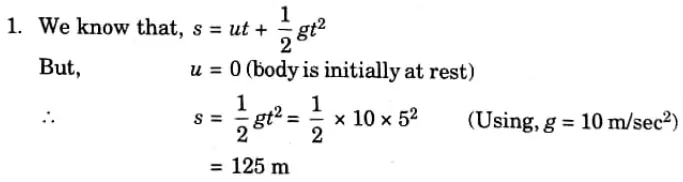
Q3. The equation of motion for motion of a particle is given by s = 18t + 3t2 – 2t3. Find acceleration and velocity at t = 2 sec.
Ans. Given: s = 18t + 3t2 – 2t3
To Find: Acceleration and velocity at t= 2 sec.
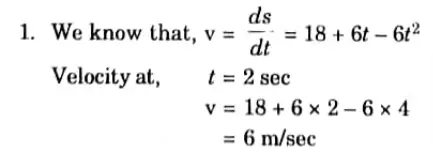
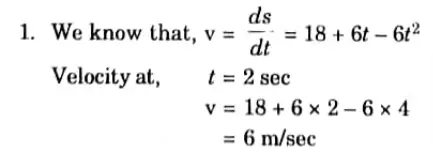
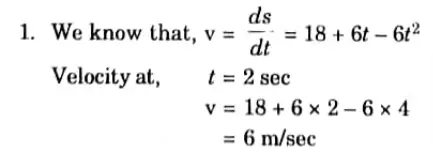
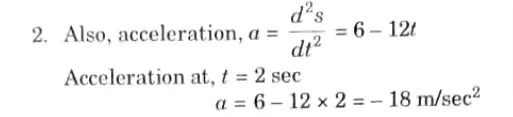
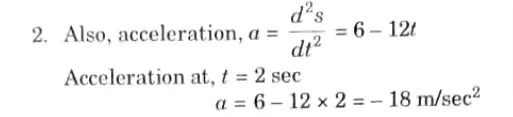
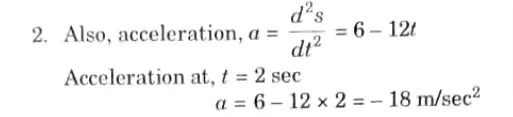
Q4. What do you understand by plane curvilinear motion?
Ans. Plane curvilinear motion is the term for a body moving in a plane in a circular route.
Q5. Define relative motion.
Ans. The relative motion of the first body with respect to the second body describes how one moving body moves in relation to another moving one.
Q6. Define work.
Ans. The result of force and displacement is called work. Joule is its measure (J).
Q7. What do you mean by energy ?
Ans. The ability to perform tasks is referred to as energy. It is the end result of time and power.
Q8. Define kinetic energy and potential energy.
Ans. Kinetic Energy : Kinetic energy is the energy that a body possesses as a result of its motion. It is given by,
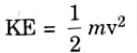
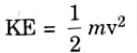
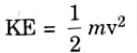
Potential Energy : Potential energy is the energy that arises from a body’s position in relation to a certain reference or datum. It is given by,
PE = mgh
Q9. Define impulse and momentum.
Ans. Impulse: Impulse is the end result of force and time.
Momentum: Momentum is the result of a body’s mass and velocity.
Q10. What do you understand by angular momentum ?
Ans. Angular momentum is the result of the rotating body’s angular velocity and mass moment of inertia.
Q11. State the law of conservation of energy. Ans. Energy cannot be created or destroyed, according to the law of conservation of energy, but it can be changed from one form into another.
Unit – 5 (Introduction to Kinetics of Rigid Bodies)
Q1. State Newton’s second law of motion.
Ans. According to Newton’s second rule of motion, a body’s rate of change in momentum is inversely proportional to the external force acting on it, and it moves in the same direction as the force.
Q2. Define instantaneous centre of rotation.
Ans. The instantaneous centre of rotation is the location where a body’s motion, which includes both translational and rotational motion, is thought to be pure rotational motion.
Q3. State and explain D’Alembert’s principle.
OR
State D-Alembert’s principle.
Ans. According to D’Alembert’s principle, the system’s net external force and the ensuing inertia force are in a condition of equilibrium.
Q4. What do you understand by work-energy principle ?
Ans. According to the work-energy principle, a body’s change in kinetic energy during any displacement is equal to the work that it does.
Q5. Write D’Alembert’s principle for rotary motion.
Ans. The algebraic sum of all the torques acting on the system as a result of external forces and reversed active forces, including the inertia torque, is zero when external torques act on a system with rotating motion, according to D’Alembert’s principle.
Q6. Give the expression for the kinetic energy of rotating bodies.
Ans.
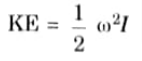
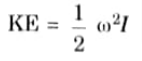
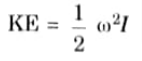
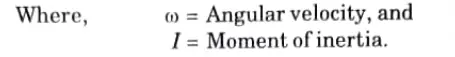
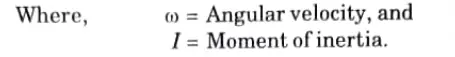
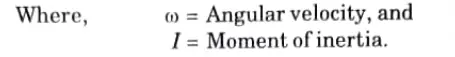
Q7. Define virtual displacement.
Ans. Virtual displacement is the movement of a partially confined body that exists only in the mind and not in reality.
Q8. Write principle of virtual work for a particle and for a rigid body.
Ans.
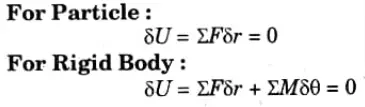
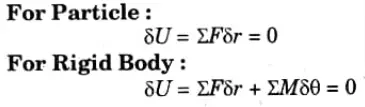
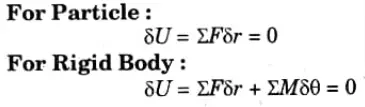
Q9. Write the different types of motion.
Ans. Following are the different types of motion:
- i. Translation,
- ii. Rotation, and
- iii. General plane motion (combined motion of translation and rotation).



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Engineering Mechanics Quantum, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Engineering Mechanics Quantum PDF: | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
