Centroid and Center of Gravity are the main topics in Engineering Mechanics Unit 2. Students will gain knowledge about how to determine the centroid and center of gravity of various forms and structures in this subject. Numerous engineering specialties, including as civil, mechanical, and aerospace engineering, depend heavily on these ideas. Students’ ability to solve problems with locating the centroid and center of gravity will be aided by the Important Questions in this course.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Engineering Mechanics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. A wire is bent into a closed loop A-B-C-D-E-A as shown in Fig. in which portion AB is circular arc. Determine the centroid of the wire.
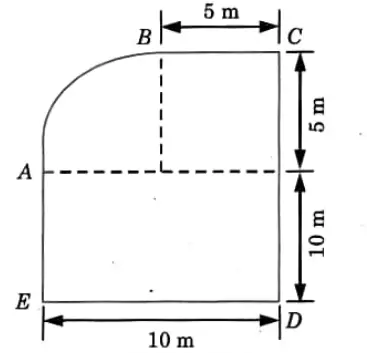


Ans. Given: Fig
To Find: Centroid of the wire.
1. Consider ED as X-axis and AE as Y-axis or AE and ED as reference axes to determine the centroid.
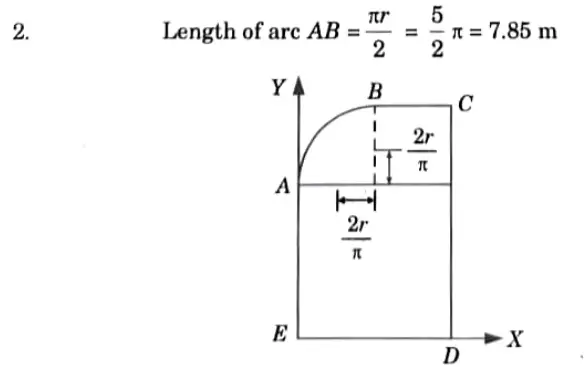


3 Position of centroid for arc,
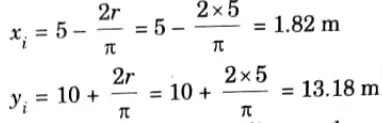
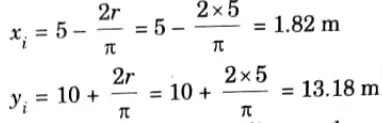
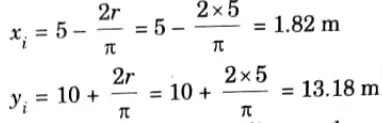
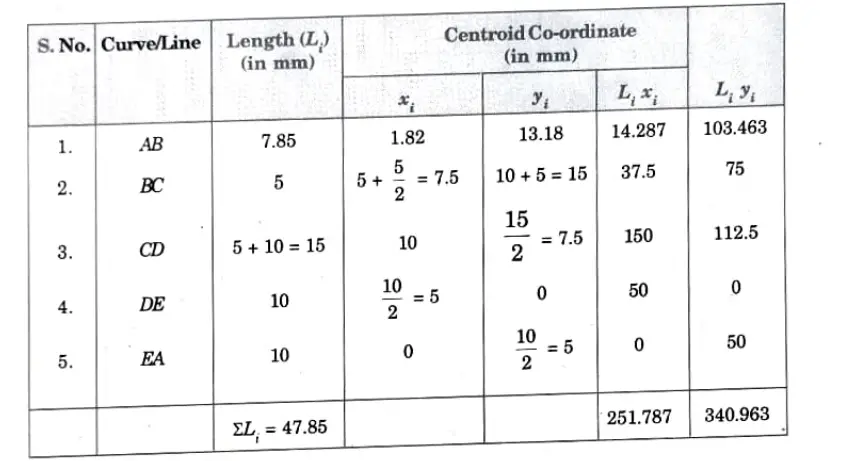
4. The coordinates for the centroid of various lines and curves are shown in table given below:


5. Centroid of the given figure is,
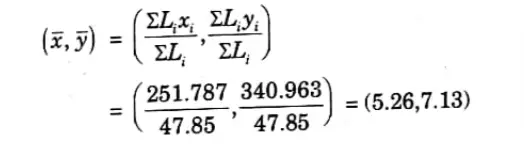
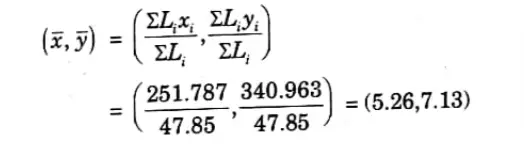
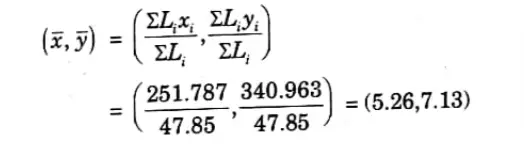
Q2. Discuss in brief about centroid of composite figures.
Ans. 1. Finding the centroid of a composite region is a common task in engineering. Such a region could be made up of standard geometric shapes like rectangles, triangles, circles, semicircles, and quarter circles, among others.
2. In these situations, we divide the area into predictable geometric shapes whose centroids are easily recognised.
3. Let Ai be the area of an element and (x̄i , ȳi) be the respective centroidal coordinates. Then for the composite area,
Q3. Find out the centroid of an L-section of 120 mm x 80 mm x 20 mm as shown in Fig.
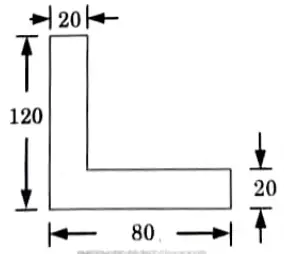


Ans. Given: Fig.
To Find: Centroid of L-section1. The given L-section is not symmetrical about any section. Hence, in this case, there will be two axes of references. The lowest line of the figure i.e., line GF) will be taken as axis of reference for calculating ȳ and the left line of the L-section (i.e., line AG) will be taken as axis of reference for calculating x̄.
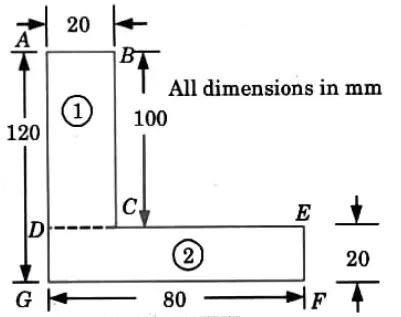


2. The given -section is split up into two rectangles ABCD and DEFG, as shown in Fig.






Hence, the centroid of the L-section is at a distance of 43.33 mm from the bottom line GF’ and 23.33 mm from the left line AG.
Q4. Define the following terms :
i. Polar moment of inertia, and
ii. Radius of gyration.
Ans. i. Polar Moment of Inertia:
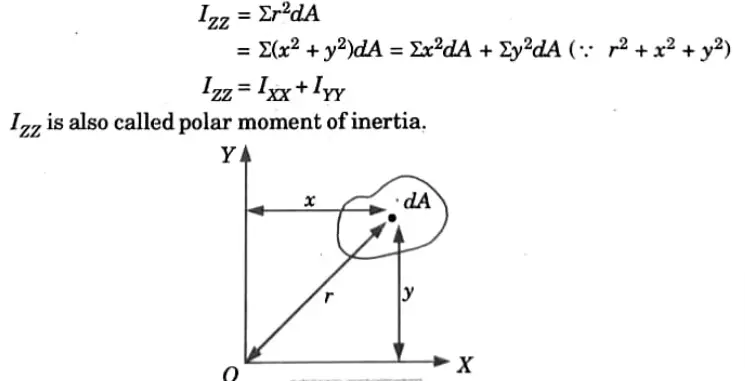
1. If an elemental area dA is at a distance r from origin of the coordinate axes then its polar moment of inertia is given by,



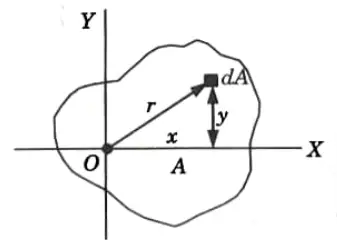


3. To put it another way, we can say that an area’s polar moment of inertia is its moment of inertia about the Z-axis.
ii. Radius of Gyration: The distance that results in the moment of inertia of that area when squared and multiplied by area is known as the radius of gyration.



Q5. State and prove perpendicular axis theorem.
Ans. A. Perpendicular Axis Theorem:
1. The polar moment of inertia is the sum of the moment of inertia about any two mutually perpendicular axes passing through the same point O and lying in the plane of the provided area. It is the moment of inertia of an area about an axis perpendicular to its plane.
B. Proof :
1. Consider an elemental area dA at distance r from point O.
2. Let dA have coordinates x and y, then from the definition,


Q6. Find the moment of inertia of a semicircle and quarter circle.
Ans. i. Moment of Inertia of a Semicircle:
a. About Diametral Axis:
- 1. If the limit of integration is put as 0 to π instead of 0 to 2 π in the derivation for the moment of inertia of a circle about diametral axis the moment of inertia of a semicircle is obtained.
- 2. It can be observed that the moment of inertia of a semicircle (Fig. 2.19.1) about the diametral axis AA’ is,
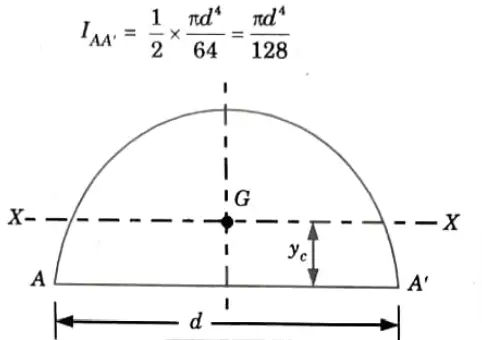


b. About Centroidal Axis X-X:
1. Now, the distance of centroidal axis yc from the diametral axis is given by,
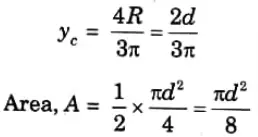
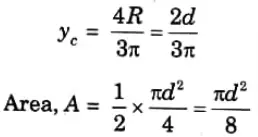
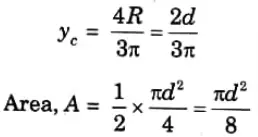
2. From parallel axis theorem,
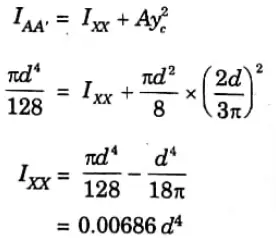
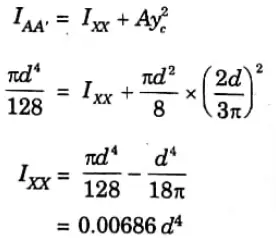
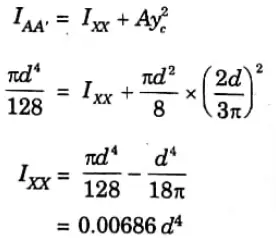
ii. Moment of Inertia of a Quarter of a Circle:
a. About the Base:
1. If the limit of integration is put as 0 to π/2 instead of 0 to 2π in the derivation for moment of inertia of a circle, the moment of inertia of a quarter of a circle is obtained.
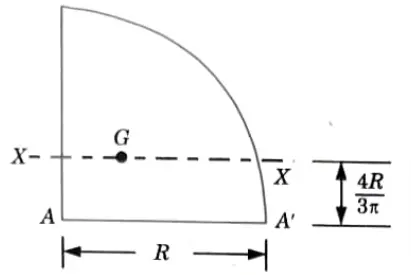


2. It can be observed that moment of inertia of the quarter of a circle about the base AA’ is,
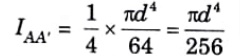
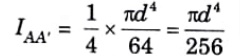
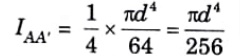
b. About Centroidal Axis X-X:
1. Now, the distance of centroidal axis yc from the base is given by
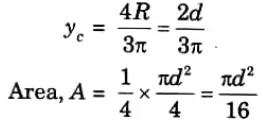
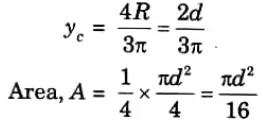
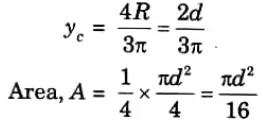
2. From parallel axis theorem,



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Engineering Mechanics Quantum, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Engineering Mechanics Quantum PDF: | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |

3 thoughts on “Important Questions for Unit 02: Centroid and Center of Gravity in Engineering Mechanics.”