Quantum Notes will reveal the secrets of algorithm design and analysis. Prepare for Aktu Btech examinations by reviewing frequently asked questions. Today, excel in your academic route! Unit-4 Dynamic Programming and Backtracking
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Design and Analysis of Algorithm: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. What is dynamic programming ? How is this approach different from recursion? Explain with example.
Ans.
- 1. Dynamic programming is a stage-wise search method suitable for optimization problems whose solutions may be viewed as the result of a sequence of decisions.
- 2. It is used when the sub-problems are not independent.
- 3. Dynamic programming takes advantage of the duplication and arranges to solve each sub-problem only once, saving the solution (in table or something) for later use.
- 4. Dynamic programming can be thought of as being the reverse of recursion. Recursion is a top-down mechanism i.e., we take a problem, split it up, and solve the smaller problems that are created. Dynamic programming is a bottom-up mechanism i.e., we solve all possible small problems and then combine them to odtain solutions for bigger problems.
Difference:
- 1. In recursion, sub-problems are solved multiple times but in dynamic programming sub-problems are solved only one time.
- 2. Recursion is slower than dynamie programming.
For example:
Consider the example of calculating nth Fibonacci number.
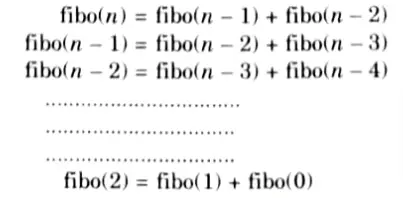
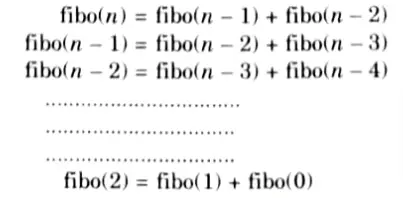
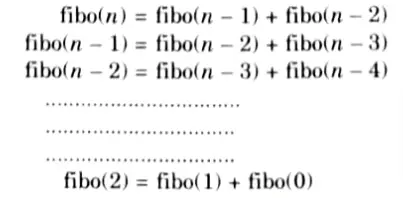
In the first three steps, it can be clearly seen that fibo (n -3) is calculated twice. If we use recursion, we calculate the same sub-problems again and again but with dynamic programming we calculate the sub-problems only once.
Q2. Discuss the elements of dynamic programming.
Ans. Following are the elements of dynamic programming:
- 1. Optimal sub-structure: Optimal sub-structure holds ifoptimal solution contains optimal solutions to sub-problems. It is often easy to show the optimal sub-problem property as follows:
- i. Split problem into sub-problems.
- ii. Sub-problems must be optimal; otherwise the optimal splitting would not have been optimal.
- iii. There is usually a suitable “space” of sub-problems. Some spaces are more “natural” than others. For matrix chain multiply we choose subproblems as sub-chains.
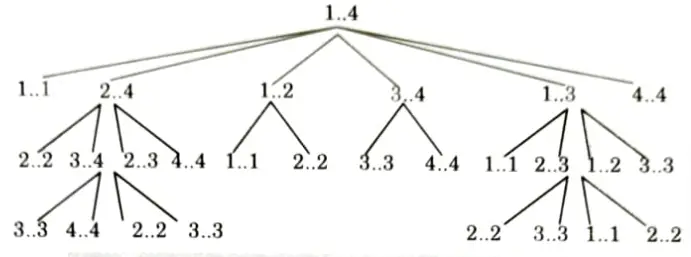
- 2. Overlapping sub-problem:
- i. Overlapping sub-problem is found in those problems where bigger problems share the same smaller problems. This means, while solving larger problems through their sub-problems we find the same sub-problems more than once. In these cases a sub-problem is usually found to be solved previously.
- ii. Overlapping sub-problems can be found in Matrix Chain Multiplication (MCM) problem.


- 3. Memoization:
- i. The memoization technique is the method of storing values of solutions to previously solved problems.
- ii. This generally means storing the values in a data structure that helps us reach them efficiently when the same problems occur during the program’s execution.
- iii. The data structure can be anything that helps us do that but generally a table is used.
Q3. What is backtracking? Write general iterative algorithm for backtracking.
Ans.
- 1. Backtracking is a general algorithm for finding all solutions to some computational problems.
- 2. Backtracking is an important tool for solving constraint satisfaction problems, such as cro5swords, verbal arithmetic, and many other puzzles.
- 3. It is often the most convenient (if not the most efficient) technique for parsing, for the knapsack problem and other combinational optimization problem.
- 4. It can be applied only for problems which admit the concept of a “partial candidate solution” and a relatively quick test ofwhether it can possibly be completed to a valid solution.
Iterative backtracking algorithm:






Q4. Write short notes on graph colouring.
Ans.
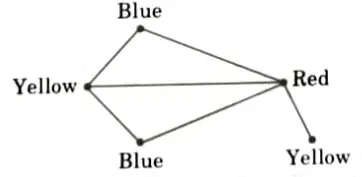
- 1. Graph colouring is a simple way of labelling graph components such as vertices, edges, and regions under some constraints.
- 2. In a graph, no two adjacent vertices, adjacent edges, or adjacent regions are coloured with minimum number of colours. This number is called the chromatic number and the graph is called a properly coloured graph.
- 3. While graph colouring, the constraints that are set on the graph are colours, order of colouring, the way of assigning colour, etc.
- 4. A colouring is given to a vertex or a particular region. Thus, the vertices or regions having same colours form independent sets.
For example:


Q5. Write pseudocode for 8-Queens problem.
Ans.
- 1. In N-Queens problem, the idea is to place queens one by one in different columns, starting from the leftmost column.
- 2. When we place a queen in a column, we check for clashes with already placed queens.
- 3. In the current column, if we find a row for which there is no clash, we mark this row and column as part of the solution.
- 4. If we do not find such a row due to clashes then we backtrack and return false.
Procedure for solving N-Queens problem:
- 1. Start from the leftmost column.
- 2. If all queens are placed return true.
- 3. Try all rows in the current column. Do following for every tried row:
- a. If the queen can be placed safely in this row then mark this Irow, columnl as part of the solution and recursively check if placing queen here leads to a solution.
- b. If placing queen in [row, column] leads to a solution then return true.
- c. If placing queen does not lead to a solution then unmark this [row, column] (backtrack) and go to step (a) to try other rows.
- 4. If all rows have been tried and nothing worked, return false to trigger backtracking.
Algorithm/pseudocode for N-Queens problem:
N-Queens are to be placed on an n xn chessboard so that no two attack i.e., no two Queens are on the same row, column or diagonal.
PLACE (k, i)
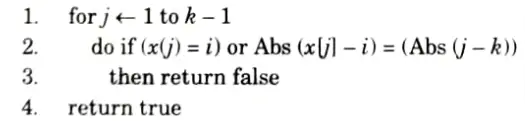
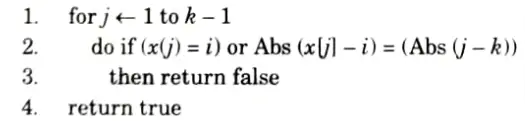
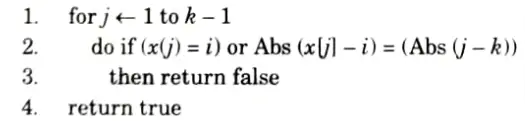
Place (k, i) returns true if a queen can be placed in the kth row and ith column otherwise return false.
x [ ] is a global array whose first k-1 values have been set. Abs(r) returns the absolute value of r.
N-Queens (k, n)
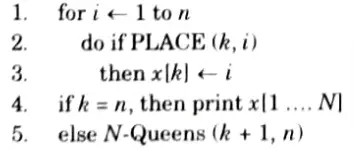
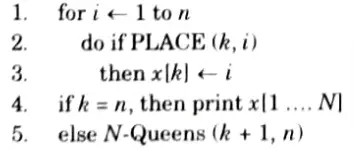
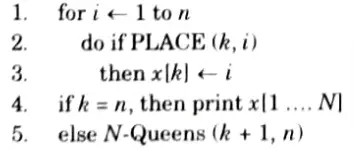
[Note: For 8-Queen problem put n = 8 in the algorithm.]
Q6. What is branch and bound technique ? Find a solution to the 4-Queens problem using branch and bound strategy. Draw the solution space using necessary bounding funetion.
Ans. Branch and bound technique:
- 1. It is a systematic method for solving optimization problems.
- 2. It is used where backtracking and greedy method fails.
- 3. It is sometimes also known as best first search.
- 4. In this approach we calculate bound at each stage and check whether it is able to give answer or not.
- 5. Branch and bound procedure requires two tools :
- a. The first one is a way of covering the feasible region by several smaller feasible sub-regions. This is known as branching.
- b. Another tool is bounding, which is a fast way of finding upper and lower bounds for the optimal solution within a feasible sub-region.
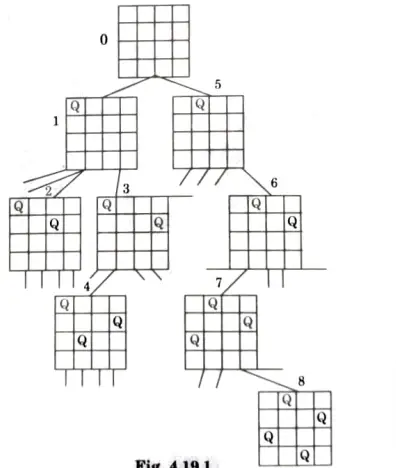
Solution to 4-Queens problem:
Basically, we have to ensure 4 things:
- 1. No two queens share a column.
- 2. No two queens share a row.
- 3. No two queens share a top-right to left-bottom diagonal.
- 4. No two queens share a top-left to bottom-right diagonal.
Number 1 is automatic because of the way we store the solution. For number 2, 3 and 4, we can perform updates in O(1) time and the whole updation process is shown in Fig.





Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Design and Analysis of Algorithm Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Design and Analysis of Algorithm Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
