With Quantum Notes, you may learn how to design and analyse algorithms. With essential, commonly asked questions, get ready for the Aktu Btech exams. Your academic career will flourish now. Unit-3 Graph Algorithms
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Design and Analysis of Algorithm: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. Describe a solution for matrix multiplication problem using divide and conquer technique.
Ans. Strassen’s matrix multiplication:
- 1. It is an application of divide and conquer technique.
- 2. Suppose we wish to compute the product C = AB where each A, B and C are n x n matrices.
- 3. Assuming that n is an exact power of 2. We divide each of A, B and C into four n/2 x n/2 matrices.
Rewriting the equation C = AB as
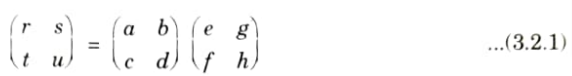
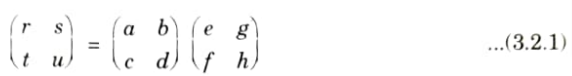
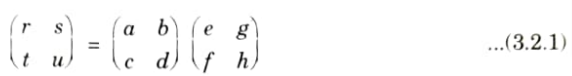
- 4. For convenience, the sub-matrices of A are labelled alphabetical from left to right, whereas those of B are labelled from top to bottom. So that matrix multiplication is performed.
Equation (3.2.1) corresponds to the four equations :



- 5. Each of these four equations specifies two multiplications of n/2 x n/2 matrices and the addition of their n/2 x n/2 products.
- 6. Using these equations to define a straight-forward divide and conquer strategy. We derive the following recurrence for the time T(n) to multiply two n x n matrices:
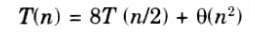
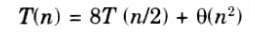
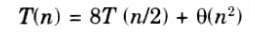
- 7. Unfortunately, this recurrence has the solution T(n) = 𝜣(n3) and thus, this method is no faster than the ordinary one.
Q2. Explain DFS. Also give DFS algorithm.
Ans. Depth First Search Algorithm:
- 1. Algorithm starts at a specific vertex S in G, which becomes current vertex.
- 2. Then algorithm traverse graph by any edge (u, v) incident to the current vertex u.
- 3. If the edge (u, v) leads to an already visited vertex v, then we backtrack to current vertex u.
- 4. If, on other hand, edge (u, v) leads to an unvisited vertex v, then we go to v and v becomes our current vertex.
- 5. We proceed in this manner until we reach to “dead end”. At this point we start backtracking.
- 6. The process terminates when backtracking leads back to the start vertex.
- 7. Edges leads to new vertex are called discovery or tree edges and edges lead to already visited vertex are called back edges.
Algorithm:
In DPS, each vertex v has two timestamps: the first timestamp d[v] ie., discovery time records when u is first discovered i.e., grayed, and the second timestamp f[u] i.e. finishing time records when the search finishes examining v’s adjacency list i.e., blacked. For every vertex dul < f[u].
DFS(G):



DFS-VISIT(u):



Q3. What are the four functions included in greedy algorithm? Write structure of greedy algorithm.
Ans. The greedy algorithm consists of four functions:
- i. A function that checks whether chosen set of items provide a solution.
- ii. A function that checks the feasibility of a set.
- iii. The selection function tells which of the candidates are most promising.
- iv. An objective function, which does not appear explicitly, gives the value of a solution.
Structure of greedy algorithm:
- i. Initially the set of chosen items is empty i.e., solution set.
- ii. At each step
- a. Item will be added in a solution set by using selection function.
- b. If the set would no longer be feasible
- Reject items under consideration (and is never consider again)
- c. Else if set is still feasible
add the current item.
Q4. What do you mean by spanning tree and minimum spanning tree ?
Ans. Spanning tree:
- 1. A spanning tree of a graph is a subgraph that contains all the vertice and is a tree.
- 2. A spanning tree of a connected graph G contains all the vertices and has the edges which connect all the vertices. So, the number of edges will be 1 less the number of nodes.
- 3. If graph is not connected, i.e., a graph with n vertices has edges less than n -1 then no spanning tree is possible.
- 4. A graph may have many spanning trees.
Minimum spanning tree:
- 1. Given a connected weighted graph G, it is often desired to create a spanning tree T for G such that the sum of the weights of the tree edges in Tis as small as possible.
- 2. Such a tree is called a minimum spanning tree and represents the “cheapest” way of connecting all the nodes in G.
- 3. There are number of techniques for creating a minimum spanning tree for a weighted graph but the most famous methods are Prim’s and Kruskal’s algorithm.
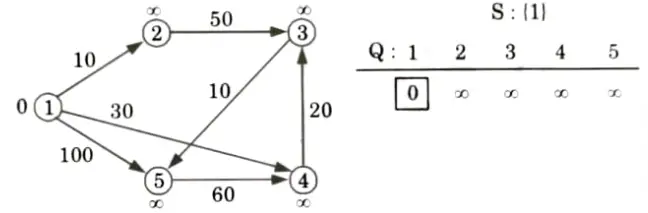
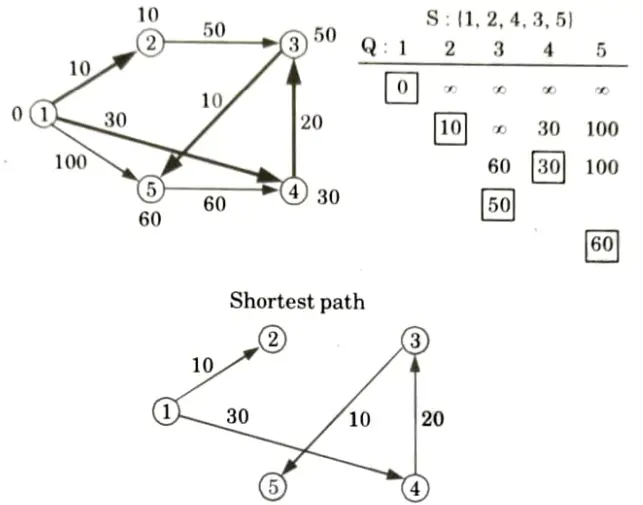
Q5. Find the shortest path in the below graph from the source vertex 1 to all other vertices by using Dijkstra’s algorithm.
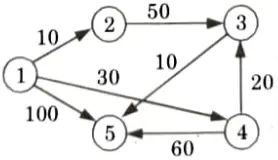


Ans. Initialize:
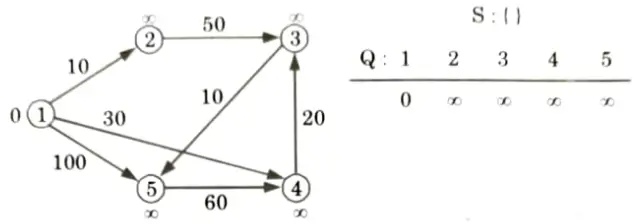


Extract min (1):


All edges leaving (1):
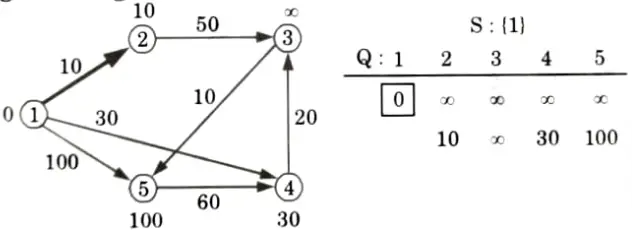


Extract min(2):
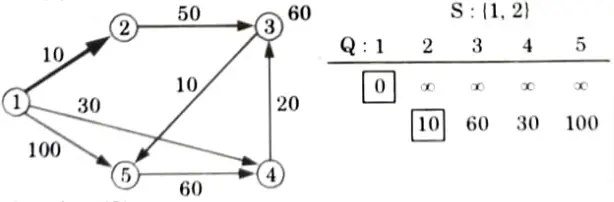


All edges leaving (2):
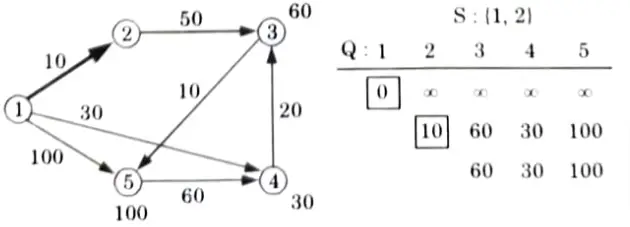


Extract min(4):
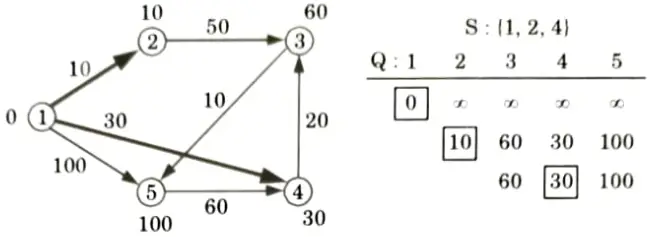


All edges leaving (4):
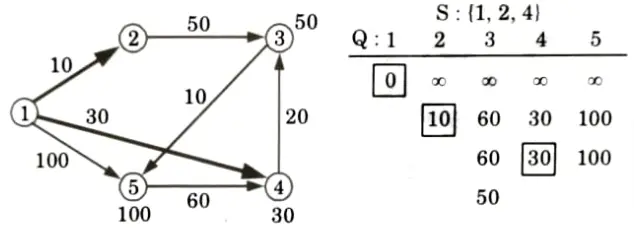


Extract min(3):
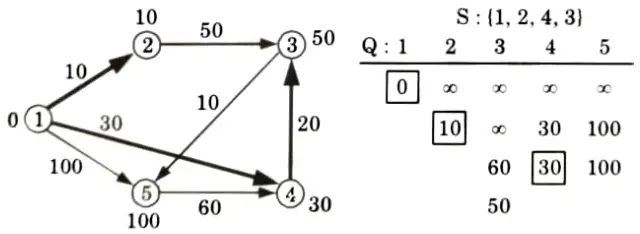


All edges leaving (3):
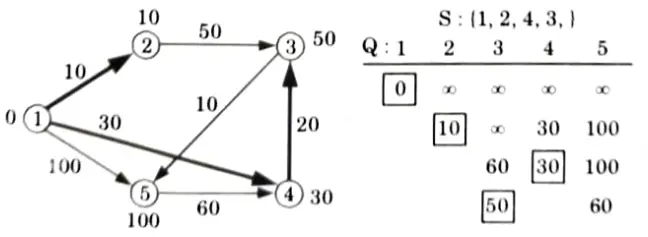


Extract min (5):


Q6. State Bellman-Ford algorithm.
Ans.
- 1. Bellman-Ford algorithm finds all shortest path length from a source s 𝜖 V to all v 𝜖 V or determines that a negative-weight cycle exists.
- 2. Bellman-Ford algorithm solves the single source shortest path problem in the general case in which edges of a given digraph G can have negative weight as long as G contains no negative cycles.
- 3. This algorithm, uses the notation of edge relaxation but does not use with greedy method.
- 4. The algorithm returns boolean TRUE if the given digraph contains no negative cycles that are reachable from source vertex otherwise it returns boolean FALSE.
Bellman-Ford (G, w, s):



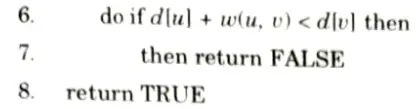
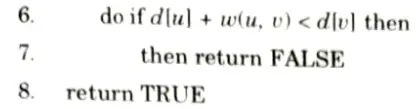
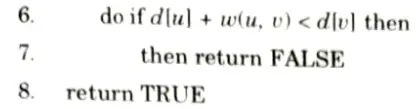
RELAX (u, v, w):
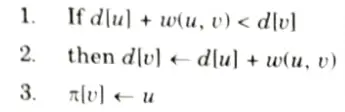
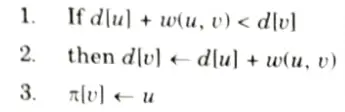
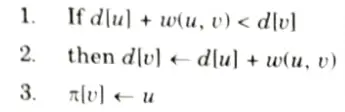
If Bellman-Ford returns true, then G forms a shortest path tree, else there exists a negative weight cycle.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Design and Analysis of Algorithm Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Design and Analysis of Algorithm Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
