The B.Tech AKTU Quantum Book Short Question Notes on Design and Analysis of Algorithm may be found here. Utilise effective methods for designing algorithms and develop knowledge to solve challenging computational issues.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Design and Analysis of Algorithm: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Unit-I: Introduction (Short Question)
Q1. Define the term algorithm.
Ans. An algorithm is a set of rules for performing calculations by hand or on a machine. It is a specific step-by-step technique for achieving a specific result.
Q2. What are the steps needed to be followed while designing an algorithm ?
Ans. Steps of designing an algorithm:
- 1. Understanding the problem.
- 2. Decision making on capabilities of computational devices.
- 3. Specification of algorithm.
- 4. Algorithm verification.
- 5. Analysis of algorithm.
- 6. Implementation or coding of algorithm.
Q3. Define the following terms:
i. Time efficiency
ii. Space efficiency
Ans. i. Time efficiency: The amount of time required to run an algorithm or programme to completion is referred to as its time efficiency.
ii. Space efficiency: The quantity of memory required to run an algorithm or programme to completion is referred to as its space efficiency.
Q4. Give an example of worst case time complexity.
Ans. By utilising the linear searching method to find a certain element, if the sought element is at the end of the list, we receive the worst time complexity.
Q5. Compare time complexity with space complexity.
Ans.
| S. No. | Time complexity | Space complexity |
| 1. | Time complexity is the amount of time required for an algorithm to complete its process. | Space complexity is the amount of memory needed for an algorithm to solve the problem. |
| 2. | It is expressed using Big| Oh(O), theta (𝛉) and omega (𝛀) notation. | It is expressed only using Big Oh (O) notation. |
Q6. What are the characteristics of the algorithm ?
Ans. Characteristics of algorithm :
- 1. Input and output: The algorithm must accept zero or more inputs and must produce at least one output.
- 2. Definiteness: Each step of algorithm must be clear and unambiguous.
- 3. Effectiveness: Every step must be basic and essential.
- 4. Finiteness: Total number of steps used in algorithm should be finite.
Q7. What do you mean by asymptotic notations ?
Ans. Asymptotic notation is a shorthand manner of representing an algorithm’s fastest and slowest running times.
Q8. Why are asymptotic notations important ?
Ans. Asymptotic notations are important because:
- i. They give a simple characterization of algorithm efficiency.
- ii. They allow the comparisons of the performances of various algorithms.
Q9. Solve the given recurrence T(n) = 4T (n/4) + n.
Ans. T(n) = 4T (n/4) + n
We will map this equation with
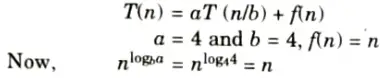
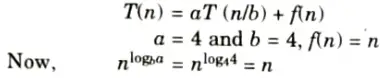
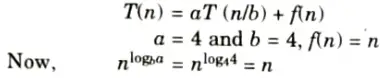
i.e., case 2 of Master’s theorem is applied. Thus, resulting solution is
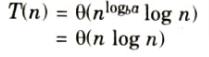
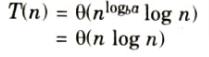
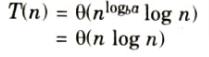
Q10. What is a heap ? What are the different types of heaps?
Ans. Heap: A heap is a specialized tree-based data structure that satisfies the heap property.
Different types of heap are:
- 1. Min-heap
- 2. Binary heap
- 3. Binomial heap
- 4. Fibonacci heap
- 5. Max-heap
- 6. Radix heap
Q11. Justify why quick sort is better than merge sort?
Ans. In theory, both quick sort and merge sort use O (n log n) time, therefore the time required to sort the items remains constant. In terms of space, however, rapid sort outperforms merge sort.
Merge sort is an in-place sorting algorithm, whereas quick sort is not. Sorting in-place ensures that no additional storage space is required. Merge sort requires a temporary array to merge the sorted arrays, hence it is not in-place.
Q12. Why counting sort is stable ?
Ans. Counting sort is stable because integers with the same value appear in the output array in the same order as they do in the input array.
Q13. What are the fundamental steps involved in algorithmic problem solving ?
Ans. Steps involved in algorithmic problem solving are:
- i. Characterize the structure of optimal solution.
- ii. Recursively define the value of an optimal solution.
- iii. By using bottom-up technique, compute value of optimal solution.
- iv. Compute an optimal solution from computed information.
Q14. Write recursive function to find nth Fibonacci number.
Ans.



Q15. Write the names of various design techniques of algorithm.
Ans. Various design techniques of algorithm are:
- 1. Divide and conquer
- 2. Greedy approach
- 3. Dynamic programming
- 4. Branch and bound
- 5. Backtracking algorithm
Q16. Solve the following recurrence using master method:
T(n) = 47T (n/3) + n2
Ans.
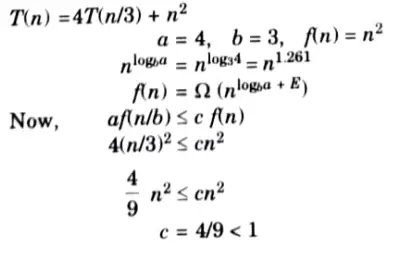
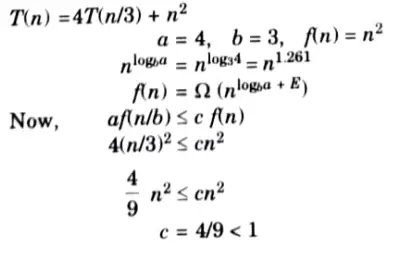
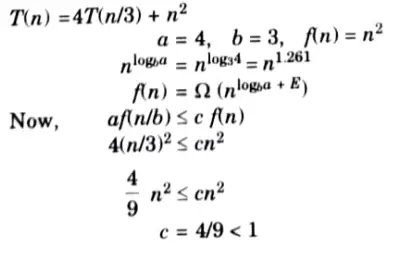
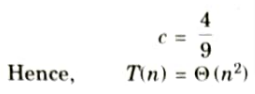
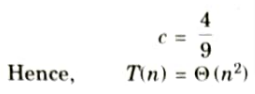
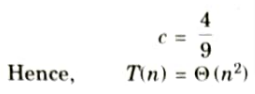
Q17. Name the sorting algorithm that is most practically used and also write its time complexity.
Ans. Quick sort algorithm is most practically used in sorting.
Time complexity of quick sort is O(n log n).
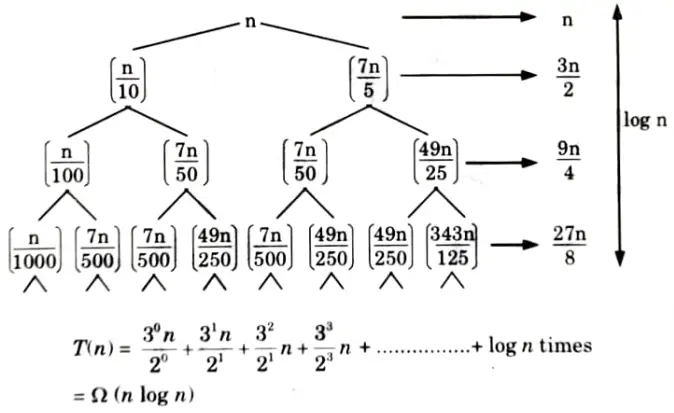
Q18. Find the time complexity of the recurrence relation
T(n) = n + T(n/10) + T(7n/5)
Ans.


Q19. What is priority queue ?
Ans. A priority queue is a collection of elements such that each element has been assigned a priority. The order in which the elements are deleted and processed according to the following rules:
i. An element of higher priority is processed before any element of lower priority.
ii. Two elements with the same priority are processed according to the order in which they were added to queue. This can be implemented as linked list, or as 2D array.
Q20. How do you compare the performance of various algorithms ?
Ans. To compare the performance of various algorithms, we first measure their performance, which is affected by the time required and the size of the task. We measure the time and space complexity of several algorithms, which are classified as worst case, average case, and best case.
Q21. Rank the following by growth rate :
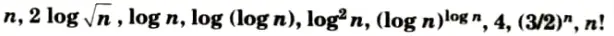
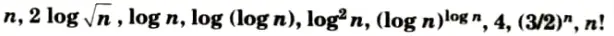
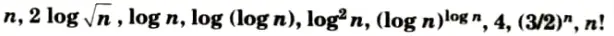
Ans. Rank in increasing order of growth rate is given as:
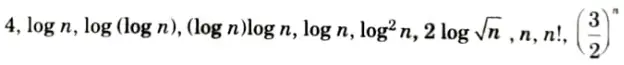
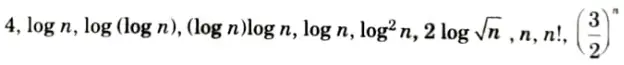
Q22. What do you mean by stability of a sorting algorithm ? Explain its application.
Ans. Stability of a sorting algorithm: Let A be an array, and let < be a strict weak ordering on the elements of A.
Sorting algorithm is stable if:
I < j and A[i] = A[j] i.e., A[i] comes before A[j].
Stability means that equivalent elements retain their relative positions, after sorting.
Application: Sorting a list with a primary and secondary key is one use for stable sorting algorithms. For example, imagine we want to sort a deck of cards so that the suits are in the order clubs, diamonds, hearts, and spades, and the cards within each suit are sorted by rank. This can be accomplished by first sorting the cards by rank (using any sort) and then by suit.
Unit-II: Advanced Data Structures (Short Question)
Q1. What are the advantages of red-black tree over binary search tree ?
Ans. The red-black tree is a self-balancing tree that guarantees O(log N) worst-case time complexity with N nodes, whereas the binary search tree guarantees O(log N) worst-case time complexity (N). As a result, searching for any node in the RB-tree becomes more efficient than searching in the binary search tree.
Q2. What is the largest possible number of internal nodes in a red-black tree with black height k?
Ans. Consider a red-black tree with black height k. If every node is black, then total number of internal nodes is 2k – 1.
Q3. Discuss the different kinds of rotations in RB-tree.
Ans. Rotations in RB-tree:
- 1. Left rotation: When left rotation on node “x” is made then its right child becomes its parent.
- 2. Right rotation: When right rotation on node “y” is made then its left child becomes its parent.
Q4. What is the running time of RB-Delete ?
Ans. Running time of RB-delete is O(log n) time.
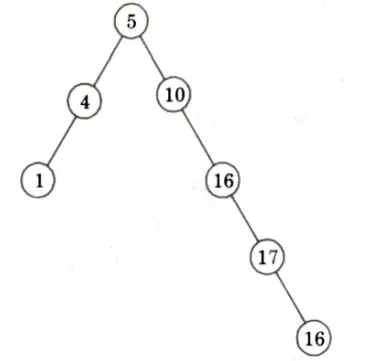
Q5. Draw BSTs of height 2,3 and 4 on the set of keys {10, 4, 5, 16, 1, 17, 21}
Ans. Keys = {10, 4, 5, 16, 1, 17, 21}
BST of height 2:
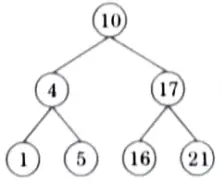


BST of height 3:
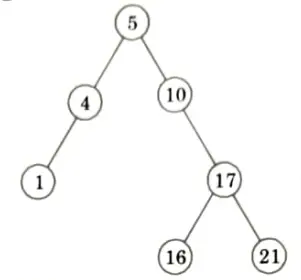


BST of height 4:


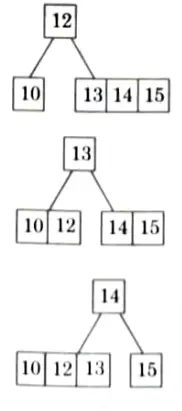
Q6. Draw all legal B-trees of minimum degree 2 that represent {10, 12, 13, 14, 15}.
Ans. Keys 10, 12,13, 14, 15
Minimum degree: 2


Q7. What are the operations performed for mergeable heaps?
Ans. Various operations performed for mergeable heaps are:
- i. Make-heap ( )
- ii. Insert (H, x)
- iii. Minimum (H)
- iv. Extract-min (H)
- v. Union (H1, H2)
Q8. Explain binomial heap with properties.
Ans. Binomial heap is a type of data structure which keeps data sorted and allows insertion and deletion in amortized time.
Properties of binomial heap:
- i. There are 2k nodes.
- ii. The height of the tree is k.
- iii. There are exactly (k/i) nodes at depth i for i = 0, 1,… k (this is why the tree is called a “binomial” tree).
- iv. Root has degree k (children) and its children are Bk-1, Bk-2,……,B0 from left to right.
Q9. Discuss the application of Fibonacci heaps.
Ans. Application of Fibonacci heaps:
- i. In Dijkstra’s algorithm for computing shortest path.
- ii. In Prim’s algorithm for finding minimum spanning tree.
Q10. What is a disjoint set ?
Ans. A disjoint set is a data structure S = {S1,……,Sk}, or a collection of disjoint dynamic sets. Each set has a representative element, which never changes unless union with another set.
Q11. Define binary heap.
Ans. The binary heap data structure is an array that represents an entire binary tree. Each node of the binary tree corresponds to an array entry. Except for the lowest level, the tree is totally filled.
Q12. Differentiate between complete binary tree and binary tree.
Ans.
| S. No. | Complete binary tree | Binary tree |
| 1. | In a complete binary tree every level, except possibly the last is completely filled, and all nodes in the last level are as far left as possible. | A binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child. |
| 2. | It can have between 1 and 2h-1 nodes at the last level h. | It can have between 2h+1 and 2h+1-1 nodes at the last level h. |
Q13. What is advantage of binary search over linear search? Also, state limitations of binary search.
Ans. Advantages of binary search over linear search:
- 1. Input data needs to be sorted in binary search but not in linear search.
- 2. Linear search does the sequential access whereas binary search access data randomly.
- 3. Time complexity of linear search is O(n) where binary search has time complexity O(log n).
Limitation of binary search:
- 1. List must be sorted.
- 2. It is more complicated to implement and test.
Q14. Prove that if n> = 1, then for any n-key B-tree of height h and minimum degree t> = 2, h <= logt (n + 1/2).
Ans. 1. The root contains at least one key.
2. All other nodes contain at least t – 1 keys.
3. There are at least 2 nodes at depth 1, at least 2t nodes at depth 2, at least 2ti-1 nodes at depth i and 2th-1 nodes at depth h.
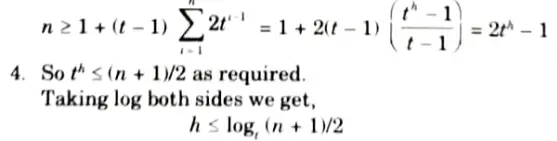
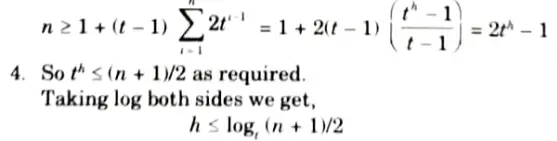
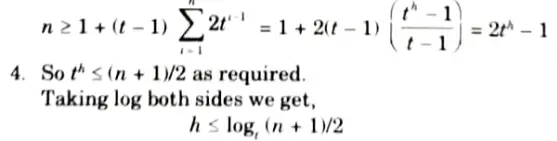
Unit-III: Graph Algorithm (Short Question)
Q1. Describe the general method for divide and conquer.
Ans. In divide and conquer method, a given problem is:
- i. Divided into smaller sub-problems.
- ii. These sub-problems are solved independently.
- iii. Combining all the solutions of sub-problems into a solution of the large problem.
Q2. Give various applications of divide and conquer.
Ans. Various applications divide and conquer strategy are:
- i. Binary search
- ii. Merge sort
- iii. Quick sort
- iv. Strassen’s matrix multiplication
- v. Finding maximum and minimum element
Q3. Describe convex hull problem.
Ans. A set of points on a plane is said to be convex if the complete line segment with end points at A and B belongs to the set for any two points A and B in the set.
Q4. Define activity selection problem.
Ans. Activity selection problem is a problem of scheduling a resource among several competing activity.
Q5. List out the disadvantages of divide and conquer algorithm.
Ans. Disadvantages of divide and conquer algorithm:
- i. Recursion is slow.
- ii. Algorithm becomes complicated for large value of n.
Q6. When we can say that optimization problem has overlapping sub-problem ?
Ans. When a recursive method returns to the same problem over and over, we say the optimisation problem has overlapping sub-problems.
Q7. Define greedy technique.
Ans. Greedy technique solves problem by making the choice that seems best at the particular moment.
Greedy technique works if a problem exhibit two properties:
- i. Greedy choice property
- ii. Optimal sub-structure
Q8. Compare between greedy method and divide and conquer algorithm.
Ans.
| S. No. | Greedy algorithm | Divide and Conquer |
| 1. | It is used to obtain optimum solution. | It is used to obtain solution to given problem. |
| 2. | In greedy method, a set of feasible solution is generated and optimum solution is picked up. | In this technique, the problem is divided into smaller sub-problems. |
Q9. How greedy method is used to solve the optimization problem ?
Ans. The greedy technique computes the solution over a series of steps. The partially formed solution is expanded in each stage. This technique is repeated until the problem is completely solved.
Q10. Give comparison between Prim’s and Kruskal’s algorithm.
Ans.
| S. No. | Prim’s algorithm | Kruskal’s algorithm |
| 1. | It is used to obtain minimum spanning tree (MSTT). | It is also used to obtain minimum spanning tree (MST). |
| 2. | It starts to build MST from any of the node. | It starts to build MST from minimum weighted edge in the graph. |
| 3. | Run faster in dense graph. | Run faster in sparse graph. |
Q11. Discuss principle of optimality.
Ans. The optimality principle states that each subsequence in an optimal sequence of decisions or choices must likewise be ideal.
Q12. Define bottleneck spanning tree.
Ans. An undirected graph bottleneck spanning tree T G is a spanning tree of G with the smallest edge weight among all spanning trees of G.
Q13. Can the minimum spanning tree change ?
Ans. Yes, the spanning tree will change only in the case when some of the weights of edges are changed.
Q14. Explain element searching techniques using divide and conquer approach.
Ans. Binary search is a search method that employs divide and conquer. The method compares the value of the centre element in the array to the input element x at each iteration. If the values match, return the middle index. Otherwise, if x is less than the middle element, call the method for the left side of the middle element recursively, else call the procedure for the right side of the middle element recursively.
Q15. What are greedy algorithms ? Explain their characteristics ?
Ans. Greedy algorithms: Greedy algorithms use a short-sighted approach in that they make judgements based on the information at hand without considering the impact these decisions may have in the future.
Characteristics of greedy algorithm:
- 1. Greedy algorithms are most efficient.
- 2. For every instance of input greedy algorithms makes a decision and continues to process further set of input.
- 3. The other input values at the instance of decision are not used in further processing.
Q16. Define feasible and optimal solution
Ans. Feasible solution: A feasible solution is a set of decision variable values that satisfy all of an optimisation problem’s constraints. The feasible region of the problem is defined as the set of all feasible solutions.
Optimal solution: A practicable optimal solution is one in which the objective function obtains its highest (or least) value.
Unit-IV: Dynamic Programming, Backtracking and Branch and Bound (Short Question)
Q1. Describe dynamic programming
Ans. Dynamic programming is a technique for solving problems with overlapping subproblems.
Q2. Give two differences between dynamic programming and divide and conquer techniques.
Ans.
| S. No. | Dynamic programming | Divide and conquer |
| 1. | Several decision sequences are formed in dynamic programming, and all overlapping sub-instances are considered. | The problem is broken down into smaller subproblems. These subproblems are tackled separately. |
| 2. | In dynamic computing, duplication in solutions is avoided totally. | In this method, duplications in subsolutions are neglected. |
Q3. Explain dynamic programming. How it is different from greedy approach ?
OR
Differentiate between greedy technique and dynamic programming.
Ans. Dynamic programming is a problem-solving technique that uses overlapping subproblems.
Problems in dynamic programming are solved by employing the divide and conquer strategy, but problems in greedy programming are solved by selecting the choice that appears best at the time.
Difference:
| S. No. | Dynamic programming | Greedy method |
| 1. | Dynamic programming is a type of ‘smart’ recursion. It is frequently necessary to divide a problem into smaller components that may be cached. | A greedy algorithm is one that performs a local optimisation at a specific moment in time. |
| 2. | Dynamic programming would solve all dependent subproblems and then choose the one that leads to the best solution. | Greedy algorithms select the subproblem that will result in the best solution locally. |
Q4. State the single source shortest path.
Ans. Single source shortest path problem states that in a given graph G = (V, E) we can find a shortest path from given source vertex s 𝜖 V to every vertex u 𝜖 V.
Q5. What is the purpose of Floyd-Warshall’s algorithm ?
Ans. Floyd-technique Warshall’s seeks the shortest path between all pairs of vertices in a graph. It employs a set of matrices of size n x n, where n is the number of vertices.
Q6. What are the constraints used for solving the problem in backtracking algorithm ?
Ans. There are two types of constraints used to solve the problem in backtracking:
- i. Explicit constraints
- ii. Implicit constraints
Q7. Write the major advantage of backtracking algorithm.
Ans. The main advantage of the backtracking technique is that it allows us to recognise that the partial vector generated does not result in an optimal solution. In this case, the vector can be ignored.
Q8. State the difference between backtracking and branch and bound.
Ans.
| S. No. | Backtracking | Branch and bound |
| 1. | Solution for backtracking is traced using depth first search. | It is not required to utilise depth first search to find the solution in this method; instead, breadth first search or best first search can be used. |
| 2. | Typically decision problems can be solved using backtracking. | Typically optimization problems can be solved using branch and bound. |
Q9. What is the running time complexity of 8-Queens problem ?
Ans. The running time complexity of 8-Queens problem is O(P(n)n!) where Pln) is polynomial in n.
Q10. Define graph colouring.
Ans. Graph colouring is a problem of colouring each vertex in graph in such a way that no two adjacent vertices have same colour and m-colours are used.
Q11. What is optimal colouring?
Ans. If the degree of given graph is d then we colour it with d + 1 colours. The least number of colours needed to colour the graph is called its chromatic number. Such type of colouring is called optimal colouring.
Q12. What is Travelling Salesman Problem (TSP) ?
Ans. The travelling salesman problem is one in which a salesman visits’m’ places in such a way that all cities must be visited at the same time, and then returns to the city from whence he started at the lowest possible cost.
Q13. Mention the three common techniques used in amortized analysis and write the characteristics of one of its technique.
Ans. Three common techniques used in amortized analysis are:
- i. Aggregate method
- ii. Accounting method
- iii. Potential method
Characteristics of aggregate method are:
- i. The amortized cost is T\n/n per operation.
- ii. It gives the average performance of each operation in the worst case.
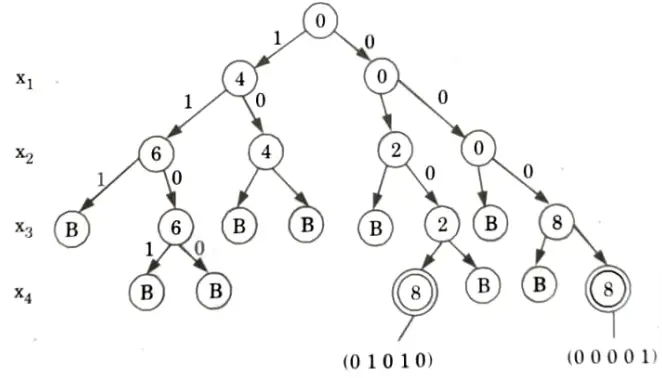
Q14. Find the subsets of sum of following problem. Given total elements are (S) = {4, 2, 7, 6, 8} and maximum SUM is (X) = 8.
Ans.


Q15. Explain application of graph colouring problem.
Ans. Application of graph colouring problem:
- 1. Sudoku: Sudoku is a type of graph colouring problem in which each cell represents a vertex. If two vertices are in the same row, column, or block, there is an edge between them.
- 2. Register allocation: Register allocation is the process of assigning a high number of target programme variables to a small number of CPU registers in compiler optimisation. This is a graph colouring problem as well.
- 3. Bipartite graphs: We can tell if a graph is bipartite or not by colouring it with two different colours. If a graph can be coloured in two ways, it is bipartite; otherwise, it is not.
- 4. Map colouring: Geography maps of countries or states in which no two nearby cities can have the same colour.
Unit-V: Selected Topics (Short Question)
Q1. Define Fast Fourier Transformation (FFT).
Ans. The Fast Fourier Transform (FFT) is an algorithm that computes an n-length vector’s Discrete Fourier Transform (DFT) in O(n log n) time. We use the divide and conquer technique to polynomial evaluation in the FFT algorithm by recognising that if n is even, we can divide a degree (n – 1) polynomial.
Q2. Discuss the term string matching.
Ans. String matching algorithms are a type of string algorithm that attempts to locate a location within a bigger string or text where one or more strings (also known as patterns) can be discovered.
Q3. Write about Knuth-Morris-Pratt algorithm.
Ans. It is the first algorithm for matching strings in linear time. We must evaluate all of the characters in the text and pattern at least once. The execution time is O(n + m).
Q4. Differentiate between decision problem and optimization problem.
Ans.
| S. No. | Decision problem | Optimization problem |
| 1. | Any problem for which answer is either yes or no is called decision problem. | Any problem that involves the identification of optimal cost is called optimization problem. |
| 2. | The algorithm for decision problem is called decision algorithm. | Typically optimization problems can be solved using branch and bound. |
Q5. Define P, NP and NP-complete in decision problems.
Ans. P-polynomial time: These problems can be solved in polynomial time, which take time like O(n), O(n2), O(n3) like finding maximum element in an array or to check whether a string is palindrome or not are P problems.
Non deterministic polynomial time: These problem cannot be solved in polynomial time like TSP (Traveling Salesman Problem) or subset sum are NP problem.
But NP problems are checkable in polynomial time means that given a solution of a problem, we can check that whether the solution is correct or not in polynomial time.
NP-complete: The group of problems which are both in NP and NP-hard are known as NP-complete problem.
Q6. Describe satisfiability.
Ans. A given boolean formula is satisfiable if there is a way to assign truth values (0 or 1) to the variable such that the final result is 1.
Q7. Define circuit satisfiability.
Ans. A combinational circuit is called circuit satisfiable if for set of inputs applied, output of this circuit should always be one.
Q8. Name some NP-complete problems.
Ans. NP-complete problems are:
- i. The 0/1 knapsack problem
- ii. Hamiltonian cycle
- iii. Travelling salesman problem
Q9. Name any three problems that cannot be solved by polynomial time algorithm.
Ans. Three problems that cannot be solved by polynomial time algorithm are:
- 1. Halting problem
- 2. Decision problem
- 3. Optimization problem
Q10. What are polynomial-time solvable and polynomial-time verifiable algorithms?
Ans. Polynomial-time solvable algorithm:
An algorithm is said to be solvable in polynomial time if the number of steps required to complete the algorithm for a given input is O(nk) for some non-negative integer k where n is the complexity of input.
Polynomial-time verifiable algorithm: A polynomial-time algorithms.A is said to be polynomial time verifiable if it has following properties:
- 1. The input to A consists of an instance I of XX is a decision problem) and a string s such that the length of s is bounded by some polynomials in the size of I.
- 2. The output of A is either yes or no.
- 3. If l is a negative instance of X. Then the output of A is “no’ regardless of the value of s.
- 4. If l is a positive instance of X1 then there is at least one choice of s for which A output “yes”.
Q11. List three problems that have polynomial time algorithm.
Ans. Problems that have polynomial time algorithm are:
- i. Binary search
- ii. Evaluation of polynomial
- iii. Sorting a list
Q12. List any two approximation algorithms.
Ans. Two approximation algorithms are:
- i. Vertex cover
- ii. Bin packing
Q13. Mention the types of randomized algorithms.
Ans. Two types of randomized algorithms are:
- i. Las Vegas algorithms
- ii. Monte Carlo algorithm
Q14. Describe the advantages of randomized algorithms.
Ans. Advantages of randomized algorithms are:
- i. These algorithms are simple to implement.
- ii. These algorithms are many times efficient than traditional algorithms.
Q15. Explain applications of FFT.
Ans. Application of Fast Fourier Transform:
- 1. Signal processing.
- 2. Image processing
- 3. Fast multiplication of large integers.
- 4. Solving Poisson’s equation nearly optimally.
Q16. What do you mean by polynomial time reduction ?
Ans. A polynomial time reduction is a method of solving one problem with the help of another. For instance, if a hypothetical subroutine exists to solve the second problem, the first problem can be handled by translating or reducing it to inputs for the second problem and invoking the subroutine one or more times.
Q17. What are approximation algorithms ? What is meant by p(n) approximation algorithms?
Ans. Approximation algorithm: An approximation algorithm is a way of dealing with NP-completeness for optimization problem. This technique does not guarantee the best solution.
p(n) approximation algorithm: A is a p(n) approximate algorithm if and only if for every instance of size n, the algorithm achieves an approximation ratio of p(n). It is applied to both maximization (0 < C (i) ≤ C*(i)) and minimization (0 < C* (i) ≤ C(i)) problem because of the maximization factor and costs are positive. pn) is always greater than 1.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Design and Analysis of Algorithm Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Design and Analysis of Algorithm Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |

1 thought on “Btech Design and Analysis of Algorithm KCS-503 Aktu Short Question, Notes Pdf”