With Quantum Notes, you can learn the secrets of algorithm design and analysis. Prepare for Aktu Btech examinations by answering frequently asked questions. Today, succeed in your academic route! Unit-5 Selected Topics
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Design and Analysis of Algorithm: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. What are the different types of string matching? Explain one of them.
Ans. Basic types of string matching algorithms are:


Naive string matching:
The Naive approach simply test all the possible placement of pattern P[1.. m] relative to text T[1 .. n]. Specifically, we try shifts s = [0, 1, .., n – m], successively and for each shift, s, compare T[s + 1 ..s +m] to P[1.. m].
Naive string matcher (T, P)



The Naive string matching procedure can be interpreted graphically as a sliding a pattern P[1. m] over the text T[1.. m] and noting for which shift all of the characters in the pattern mateh the corresponding characters in the text.
To analyze the time of Naive matching, the given algorithm is implemented as follows, note that in this implementation, we use notation P[1.. j] to denote the substring of P from index i to index j. That is, P[1 … j] = P[i] P[i +1] P[j].
Naive string matcher (T, P)
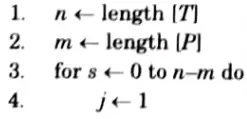
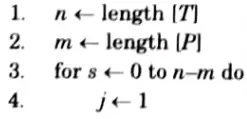
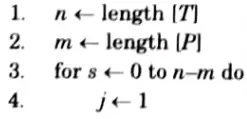
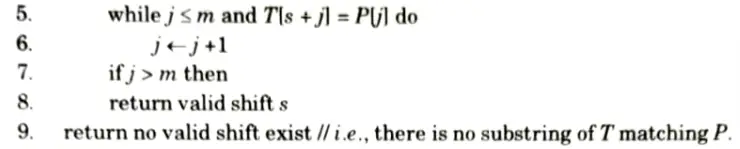
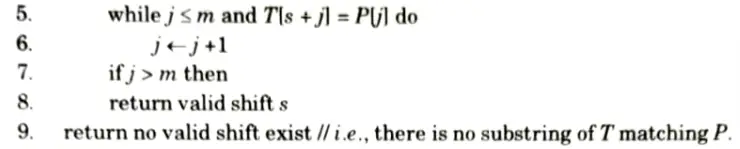
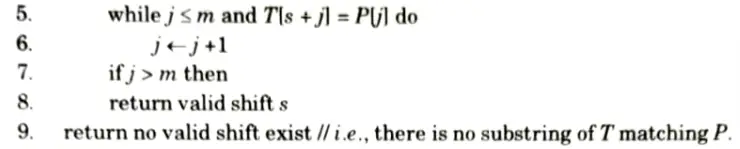
Q2. Discuss the problem classes P, NP and NP-complete.
Ans. P: Class P are the problems which can be solved in polynomial time, which take time like O(n), O(n2), O(n3).
Example: Finding maximum element in an array or to check whether a string is palindrome or not. So, there are many problems which can be solved in polynomial time.
NP: Class NP are the problems which cannot be solved in polynomial time like TSP (travelling salesman problem).
Example: Subset sum problem is best example of NP in which given a set of numbers, does there exist a subset whose sum is zero, but NP problems are checkable in polynomial time means that given a solution of a problem, we can check that whether the solution is correct or not in polynomial time.
NP-complete: The group of problems which are both in NP and NP-hard are known as NP-complete problem.
Now suppose we have a NP-complete problem R and it is reducible to then Qis at least as hard as R and since R is an NP-hard problem, therefore Qwill also be at least NP-hard, it may be NP-complete also.
Q3. Differentiate NP-complete with NP-hard.
Ans.
| S. No. | NP-complete | NP hard |
| 1. | An NP-complete problems is one to which every other polynomial-time nondeterministic algorithm can be reduced in polynomial time. | NP-hard problems is one to which an NP-complete problem is Turing-reducible. |
| 2. | NP-complete problems do not corresponds to an NP-hard problem. | NP-hard problems correspond to an NP-conmplete problem. |
| 3. | NP-complete problems are exclusively decision problem. | NP-hard problems need not to be decision problem. |
| 4. | NP-complete problems have to be in NP-hard and also in NP. | NP-hard problems do not have to be in NP. |
| 5. | For example: 3-SAT vertex cover problem is NP-complete. | For example: Halting problem is NP-hard. |
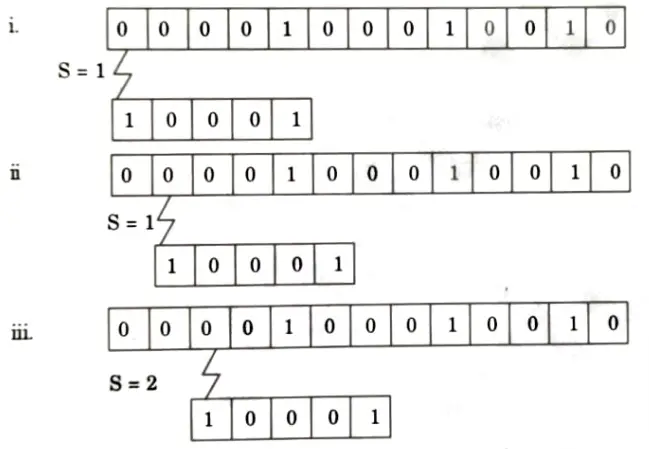
Q4. Show the comparisons that Naive string matcher makes for the pattern P = {10001} in the text T= {0000100010010}
Ans. Given, P = 10001
T = 0000100010010


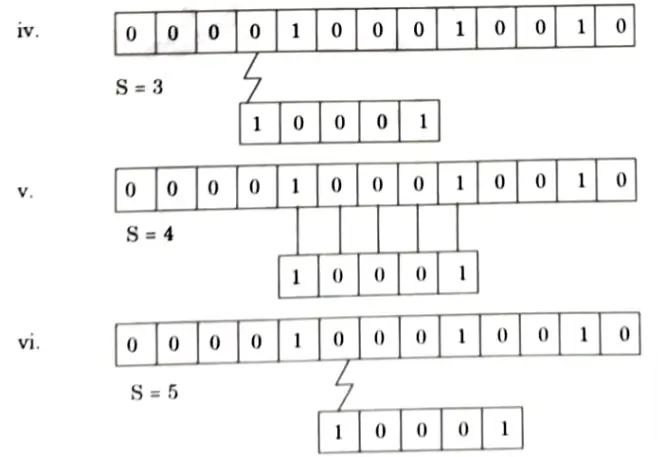


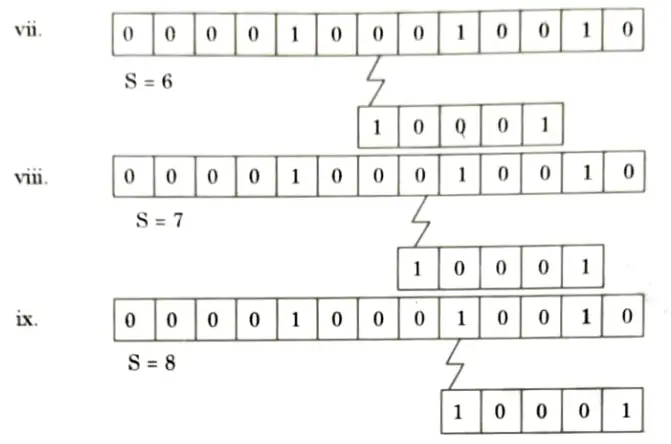


Q5. Write down Knuth-Morris-Pratt algorithm for string matching. Find the prefix function of the string ababababca.
Ans. Knuth-Morris-Pratt algorithm for string matehing:
COMPUTE-PREFIX-FUNCTION (P)
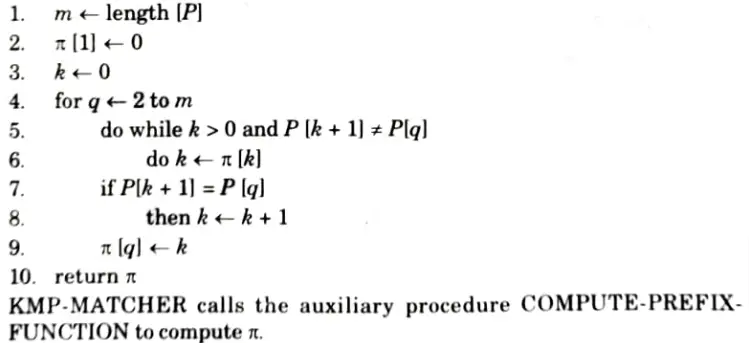
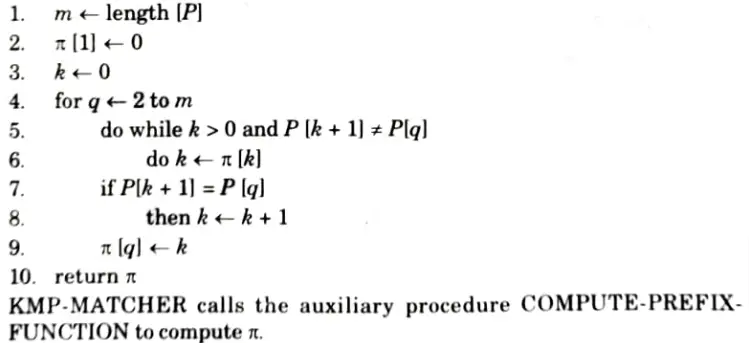
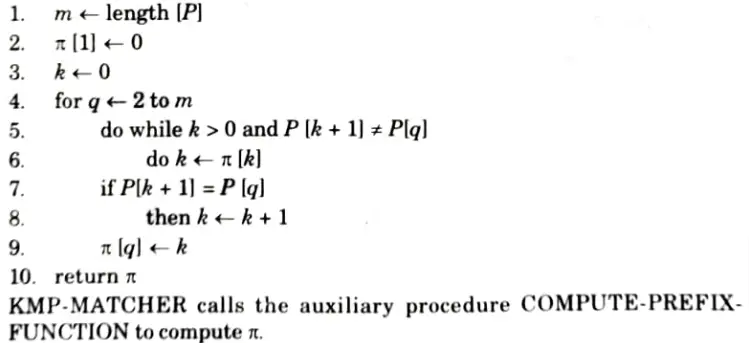
KMP-MATCHER (T, p)
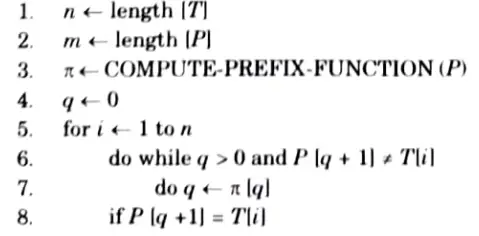
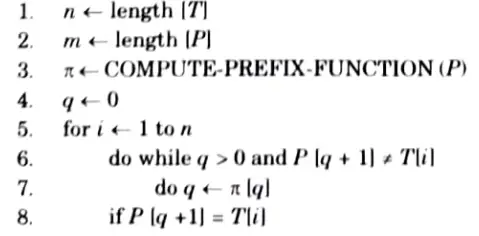
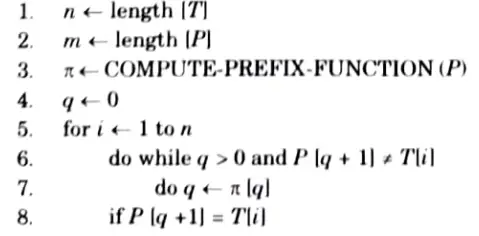
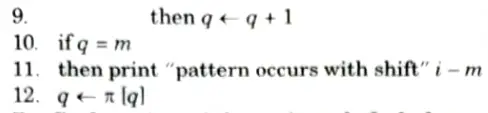
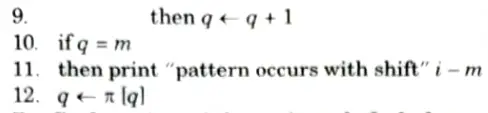
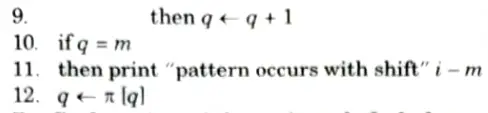
Prefix function of the string ababababea:
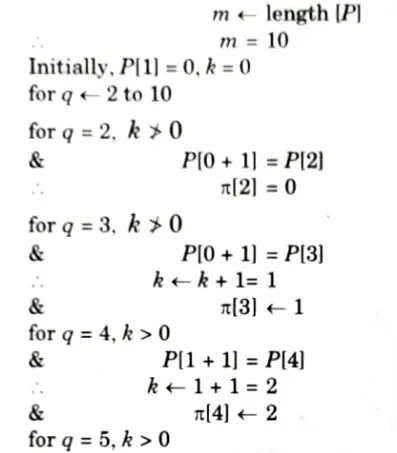
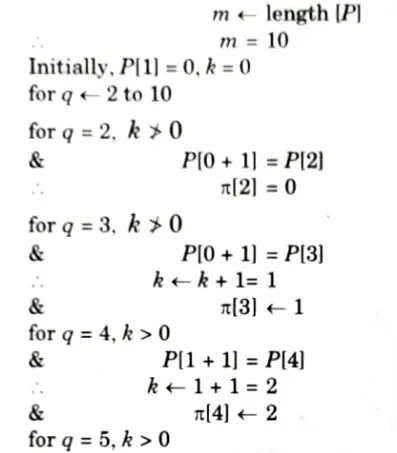
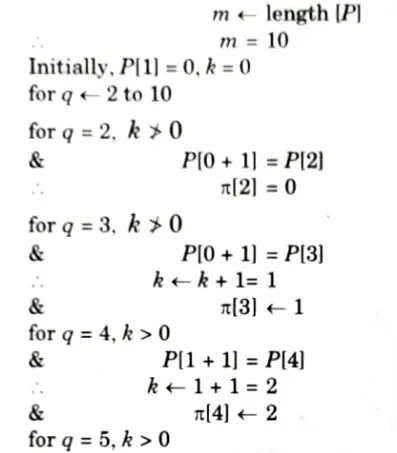
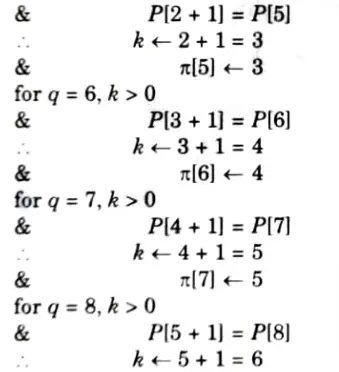
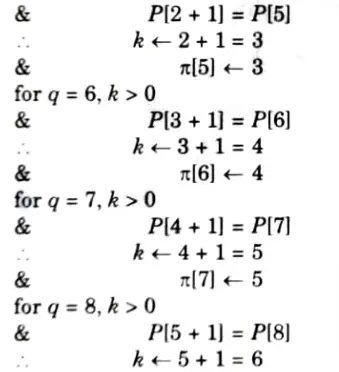
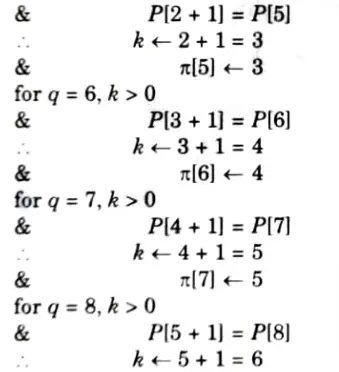
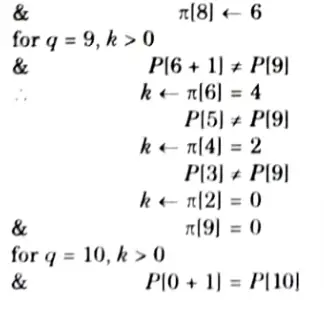
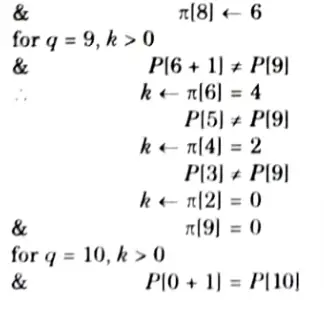
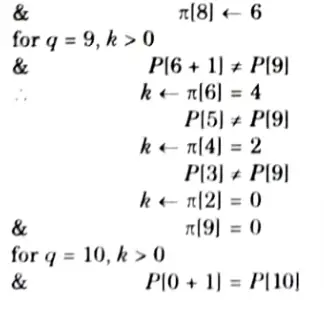
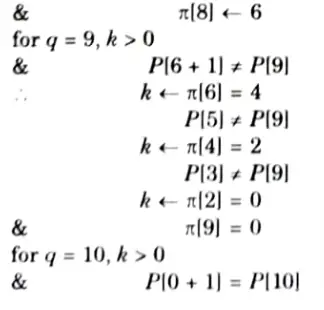
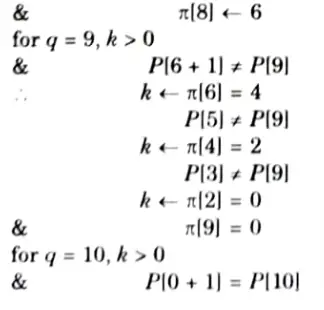
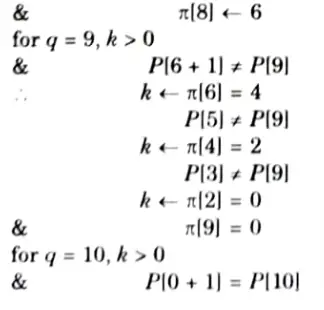
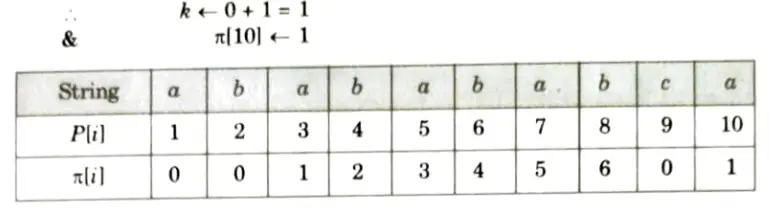


Q6. Write a short note on randomized algorithm. Write itss merits, and applications.
Ans. Randomized algorithm:
- 1. A randomized algorithm is defined as an algorithm that is allowed to access a source of independent, unbiased bits and it is then allowed to use these random bits to influence its computation.
- 2. An algorithm is randomized ifits output is determined by the input as well as the values produced by a random number generator.
- 3. A randomized algorithm makes use of a randomizer such as a random number generator.
- 4. The execution time of a randomized algorithm could also vary from run to run for the same input.
- 5. The algorithm typically uses the random bits as an auxiliary input to guide its behaviour in the hope of achieving good performance in the “average case”.
- 6. Randomized algorithms are particularly useful when it faces a malicious attacker who deliberately tries to feed a bad input to the algorithm.
Merits:
- 1. Simple.
- 2. High efficiency.
- 3. Better complexity bounds.
- 4. Random selection of good and bad choices.
- 5. Cost efficient.
Applications:
- 1. Randomized quick sort algorithm
- 2. Randomized minimum-cut algorithm
- 3. Randomized algorithm for N-Queens problem
- 4. Randomized algorithm for majority element



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Design and Analysis of Algorithm Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Design and Analysis of Algorithm Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
