Design and Analysis of Algorithm Aktu Question Paper Quantum Notes Pdf 22-23

Design and Analysis of Algorithm Important Questions 2022–2023 in Quantum Book Pdf with Solved Exam Paper, Repetition of Most Important Questions, Syllabus, and Aktu Notes

Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well.

Important Questions For Design and Analysis of Algorithm:
* Aktu Quantum          * B.tech-Syllabus
* Circulars                     * B.tech AKTU RESULT
* Btech 3rd Year

Section A: Design and Analysis of Algorithm Aktu Notes Short Answers

a. How analyze the performance of an algorithm in different cases ?

Ans. Analysis/complexity of an algorithm: 

The complexity of an algorithm is a function g(n) that gives the upper bound of the number of operation (or running time) performed by an algorithm when the input size is n.

Types of complexity: 

Space complexity: Space complexity of an algorithm is the amount of memory it needs to run to complection, including the space for input values for execution.

Time complexity: Time complexity of an algorithm is the number of times a statement executes. It is not the actual time required to execute a particular code. 

Cases of complexity:

• 1. Worst case: It is the upper bound on the running time of an algorithm. It is the case that causes a maximum number of operation to be executed.
• 2. Average case complexity: The running time for any given size input will be the average number of operations over all problem instances for a given size.
• 3. Best case complexity: The best case complexity of the algorithm is the function defined by the minimum number of steps taken on any instance of size n.  

b. Derive the time complexity of merge sort.

Ans. 

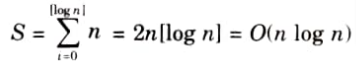
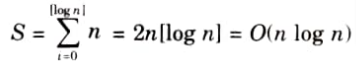
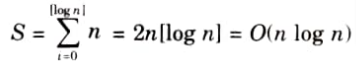
c. Explain left rotation in RB tree. 

Ans.

• 1. In rotation operation, the positions of the nodes of a subtree are interchanged. 
• 2. Rotation operation is used for maintaining the properties of a red black tree when they are violated by other operations such as insertion and deletion. 
• 3. In left-rotation, the arrangement of the nodes on the right is transformed into the arrangements on the left node.  

d. Write down the properties of Fibonacci Heap. 

Ans. Fibonacci Heap is a collection of trees with min-heap or max-heap property. In Fibonacci Heap, trees can have any shape even all trees can be single nodes. Fibonacci Heap maintains a pointer to minimum value (which is root of a tree). 

e. Explain greedy programming in brief.  

Ans. Greedy is an algorithmic paradigm that builds up a solution piece by piece, always choosing the next piece that offers the most obvious and immediate benefit. So the problems where choosing locally optimal also leads to global solution are best fit for Greedy. 

A Greedy algorithm makes greedy choices at each step to ensure that the objective function is optimized. 

f. What do you mean by convex hull ?

Ans. There exists a set of points on a plane which is said to be convex if for any two pointsA and B in the set, the entire line segment with the end points at A and B belongs to the set.

g. Write down the Floyd Warshal algorithm. 

Ans. 

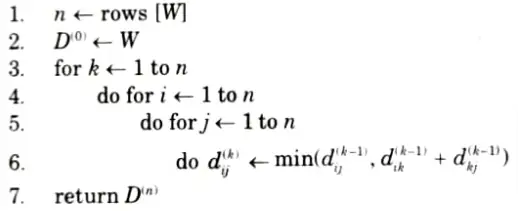
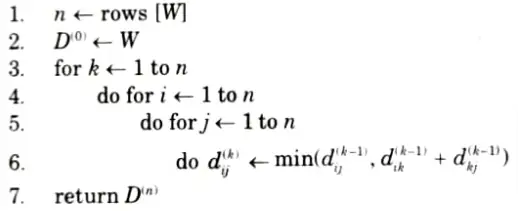
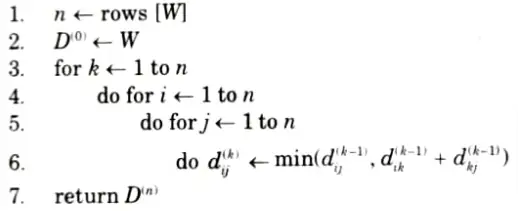
h. Explain branch and bound method in brief. 

Ans. Branch and bound is one of the techniques used for problem solving. It is similar to the backtracking since it also uses the state space tree. It is used for solving the optimization problems and minimization problems. If we have given a maximization problem then we can convert it using the Branch and bound technique.  

i. Explain randomized algorithm in brief. 

Ans.

• 1. A randomized algorithm is defined as an algorithm that is allowed to access a source of independent, unbiased bits and it is then allowed to use these random bits to influence its computation. 
• 2. An algorithm is randomized if its output is determined by the input as well as the values produced by a random number generator.
•  3. A randomized algorithm makes use of a randomizer such as a random number generator.
• 4. The execution time of a randomized algorithm could also vary from run to run for the same input. 
• 5. The algorithm typically uses the random bits as an auxiliary input to guide its behaviour in the hope of achieving good performance in the “average case”.
• 6. Randomized algorithms are particularly useful when it faces a malicious attacker who deliberately tries to feed a bad input to the algorithm. 

j. Explain NP-complete and NP-Hard. 

Ans. NP-complete : The group of problems which are both in NP and NP-hard are known as NP-complete problem. 

NP-Hard: 

• 1. We say that a decision problem P_i is NP-hard if every problem in NP is polynomial time reducible to P_i.
• 2. In symbols,

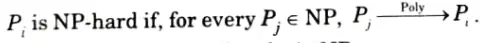
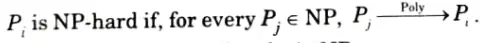
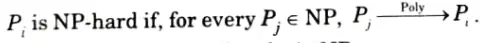
• 3. This does not require P_i to be in NP.
• 4. Highly informally, it means that P_i is ‘as hard as’ all the problem in NP.  
• 5. If P_i can be solved in polynomial time, then all problems in NP.
• 6. Existence of a polynomial time algorithm for an NP-hard problem implies the existence of polynomial solution for every problem in NP.  

Section B: Aktu Long Questions of Design and Analysis of Algorithm

a. Solve the recurrence  

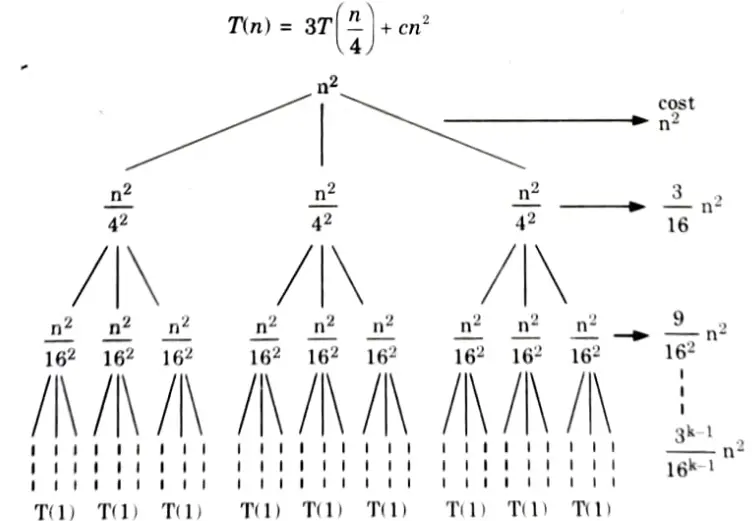
i. T (n) = 3T (n/4) + cn² using recursion tree method. 

ii. T (n) =n + 2T (n/2) using iteration method. (Given T (1) = 1) 

Ans. i. 

ii. 

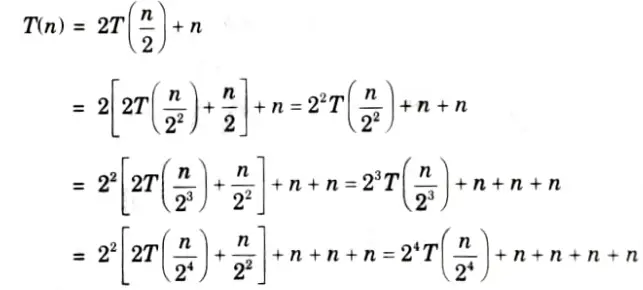
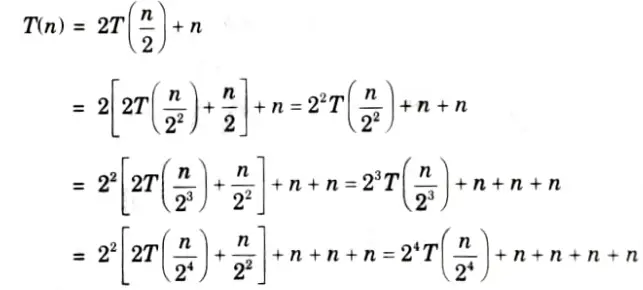
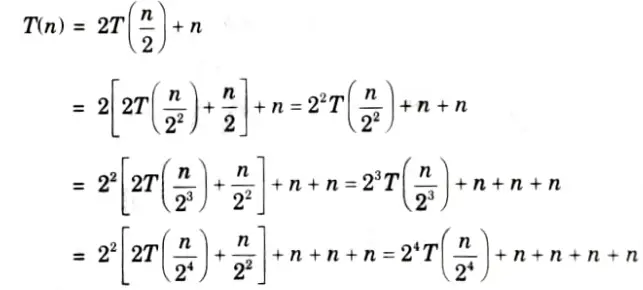
Repeat upto k times  

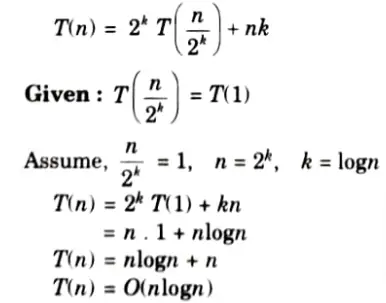
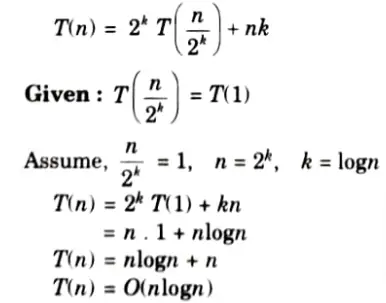
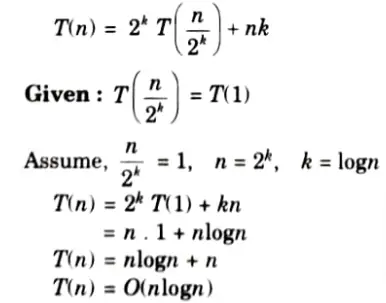
b. What is Binomial Heap ? Write down the algorithm for decrease key operation in Binomial Heap also write its time complexity. 

Ans. Binomial heap: 

1. Binomial heap is a type of data structure which keeps data sorted and allows insertion and deletion in amortized time. 

2. A binomial heap is implemented as a collection of binomial tree.  

Decrease key operation: BINOMIAL-HEAP-DECREASE-KEY (H, x, k) 

Deleting a key: The operation BINOMIAL-HEAP-DELETE (H,x) is used to delete a node x’s key from the given binomial heap H. The following implementation assumes that no node currently in the binomial heap has a key of – ∞. 

BINOMIAL-HEAP-DELETE (H, x) 

1. BINOMIAL-HEAP-DECREASE-KEY (H, x, ∞) 

2. BINOMIAL-HEAP-EXTRACT-MINED 

Time complexity: The time complexity of finding the minimum key in binomial heap is O(logn).

c. Write and explain the Kruskal algorithm to find the Minimum Spanning Tree of a graph with suitable example. 

Ans. Kruskal algorithm: 

i. In this algorithm, we choose an edge of G which has smallest weight among the edges of G which are not loops. 

ii. This algorithm gives an acyclic subgraph T of G and the theorem given below proves that Tis minimal spanning tree of G. Following steps are required:

Step1: Choose e₁, an edge of G, such that weight of e₁ w(e₁) is as small as possible and e₁ is not a loop. 

Step 2: If edges e₁,e₂,……..,e_i have been selected then choose an edge e_i+1 not already chosen such that

Step 3: If G has n vertices, stop after n – 1 edges have been chosen. Otherwise repeat step 2.

If G be a weighted connected graph in which the weight of the edges areall non-negative numbers, let T be a subgraph of G obtained by Kruskal’s algorithm then, T is minimal spanning tree.

Example:

Step 1: Arrange the edge of graph according to weight in ascending order. 

Step 2: Now draw the vertices as given in graph, 

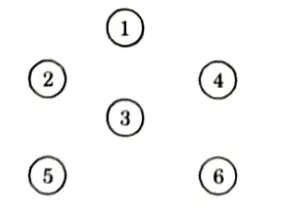
Now draw the edge according to the ascending order of weight. If any edge forms cycle, leave that edge. 

Step 3: Select edge 13 

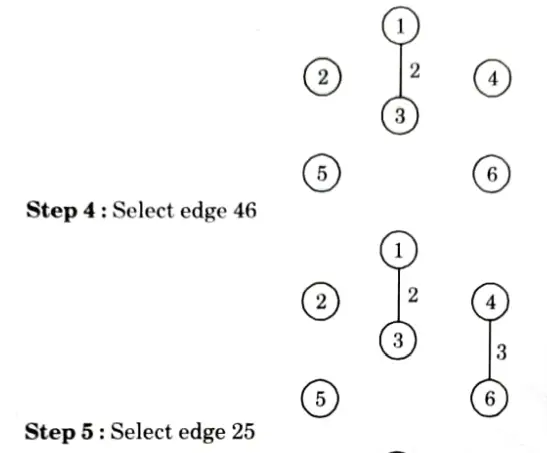
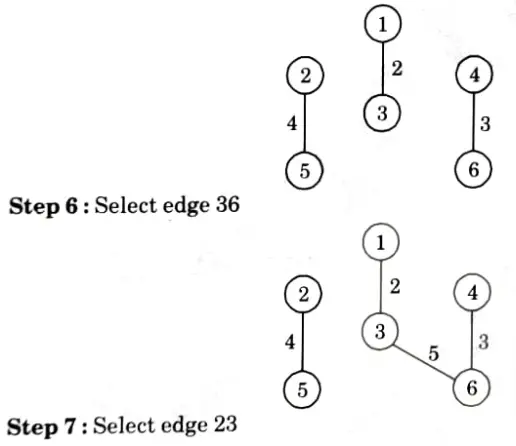
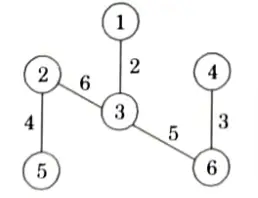
All the remaining edges, such as 34, 41, 12, 35, 56 are rejected because they form cycle. 

All the vertices are covered in this tree. So, the final tree with minimum cost of given graph is 

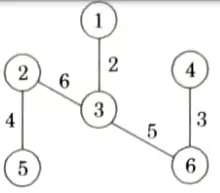
Minimum cost = 2+3+ 4+ 5 +6 20 

d. What is N queens problem ? Draw a state space tree for 4 queens problem using backtracking. 

Ans. N-Queens problem:

• 1. In N-Queens problem, the idea is to place queens one by one in different columns, starting from the leftmost column.
• 2. When we place a queen in a column, we check for clashes with already placed queens.
• 3. In the current column, if we find a row for which there is no clash, we mark this row and column as part of the solution.
• 4. If we do not find such a row due to clashes then we backtrack and return false. 

4-Queens problem:

• 1. Suppose we have 4 x 4 chessboard with 4-queens each to be placed in non-attacking position.  

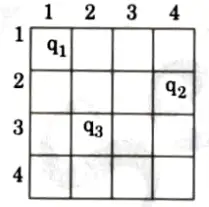
• 2. Now, we will place each queen on a different row such that no two queens attack each other.
• 3. We place the queen q₁ in the very first accept position (1, 1).
• 4. Now if we place queen q₂ in column 1 and 2 then the dead end is encountered.  
• 5. Thus, the first acceptable position for queen q₂ is column 3 ie., (2, 3) but then no position is left for placing queen q₃ safely. So, we backtrack one step and place the queen q₂ in (2, 4). 
• 6. Now, we obtain the position for placing queen q₃ which is (3, 2). But later this position lead to dead end and no place is found where queen q₂ can be placed safely.  

• 7. Then we have to backtrack till queen q₁ and place it to (1, 2) and then all the other queens are placed safely by moving queen q₂ to (2, 4), queen q₃ to (3, 1) and queen q₄ to (4, 3) i.e., we get the solution < 2, 4, 1, 3>. This is one possible solution for 4-queens problem. 

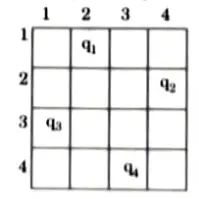
• 8. For other possible solution the whole method is repeated for all partial solutions. The other solution for 4-queens problem is <3, 1, 4, 2> i.e., 

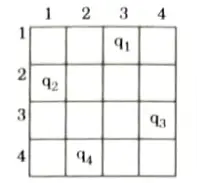
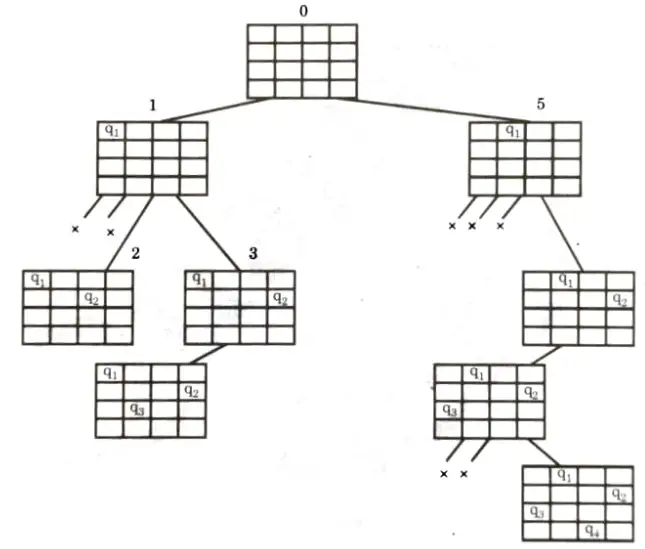
• 9. Now, the implicit tree for 4-queen for solution <2, 4, 1,3> is as follows: 
• 10. Fig. shows the complete state space for 4-queens problem. But we can use backtracking method to generate the necessary node and stop if next node violates the rule i.e., if two queens are attacking.  

Section 3: Design and Analysis of Algorithm Quantum Pdf

a. Write merge sort algorithm and sort the following sequence {23, 11, 5, 15, 68, 31,4, 17} using merge sort.

Ans. Merge sort algorithm:

• 1. Merge sort is a sorting algorithm that uses the idea of divide and conquer.
• 2. This algorithm divides the array into two halves, sorts them separately and then merges them.
• 3. This procedure is recursive, with the base criteria that the number of elements in the array is not more than 1. 

Algorithm: 

MERGE_SORT (a,p, r) 

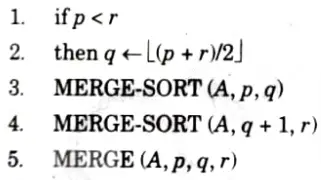
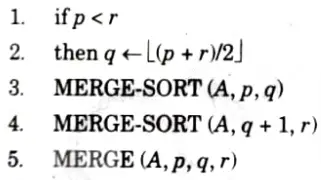
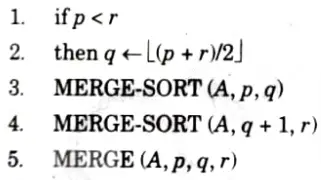
MERGE (A,p, q,r) 

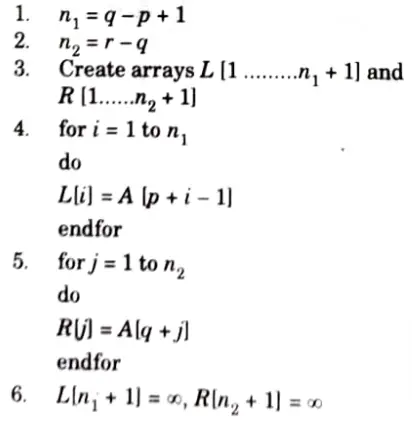
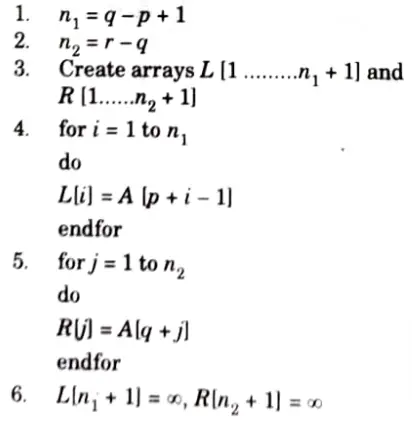
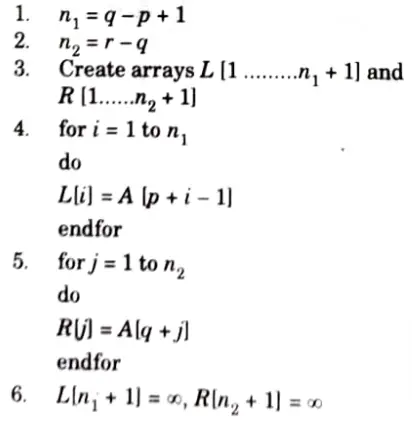
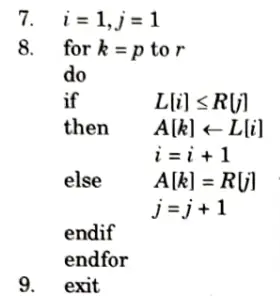
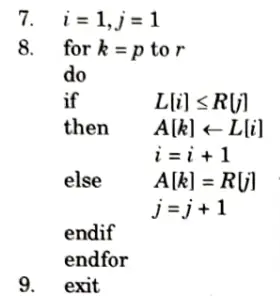
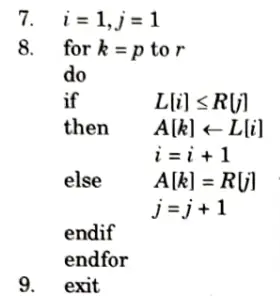
Numerical: 

Given array: {23, 11, 5, 15, 68, 31, 4, 17}

1. Divide into two halves:

2. Consider first part: Again divide into two sub arrays 

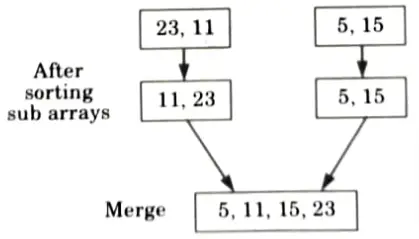
3. Consider the second half: Again divide into two sub arrays 

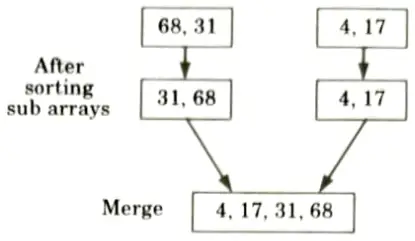
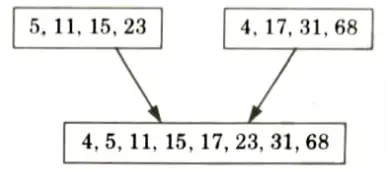
4. Merge these two sorted sub arrays 

b. What do you understand by stable and unstable sorting? Sort the following sequence {25, 57, 48, 36, 12, 91, 86, 32} using heap sort. 

Ans. Stable sorting: 

• 1. A sorting algorithm is said to be stable if two objects with equal keys appear in the same order in sorted output as they appear in the input sorted array.
• 2. A stable sort is one where the initial order of equal items is preserved.
• 3. Some sorting algorithms are stable by nature, such as bubble sort, insertion sort, merge sort, counting sort etc.
• 4. Let A be an array, and let < be a strict weak ordering on the elements of A. Sorting algorithm is stable if:

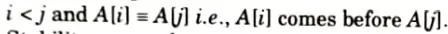
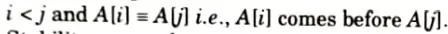
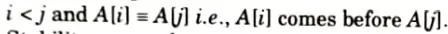
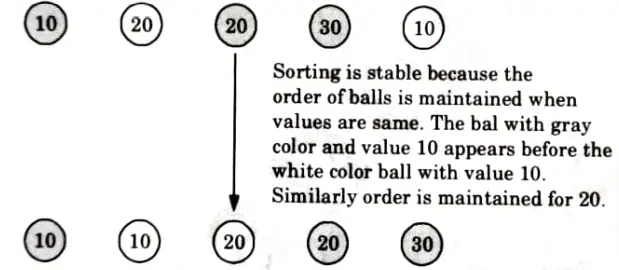
• 5. Stability means that equivalent elements retain their relative positions, after sorting.  

For example:  

Unstable sorting: In an unstable sorting algorithm the ordering of the same values is not necessarily preserved after sorting. 

Unstable sorting 

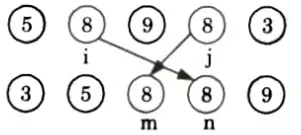
Sorting algorithms which are not considered stable are selection sort, shellsort, Quicksort, Heapsort. 

Numerical: 

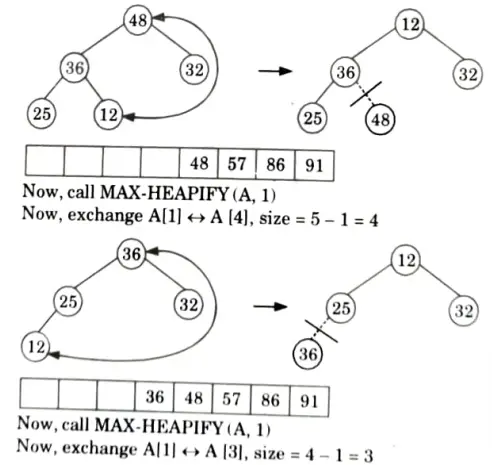
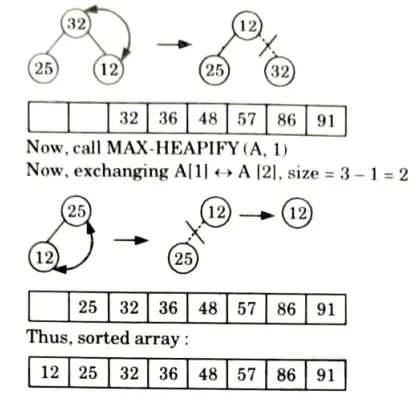
Originally the given array: A[25, 57, 48, 36, 12, 91, 86, 32]

First we call BUILD-MAX HEAP

heap size [A] = 8

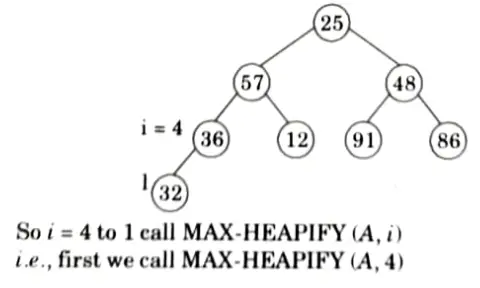
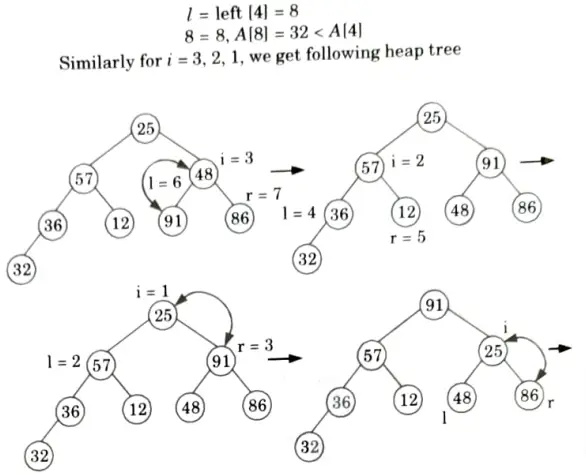
So, final tree after BUILD-MAX heap is 

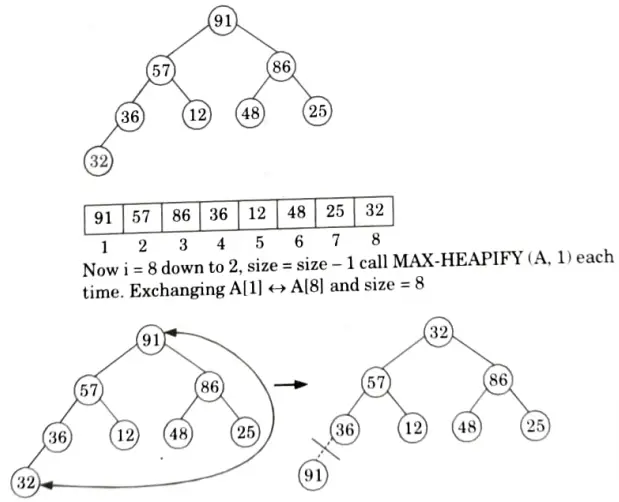
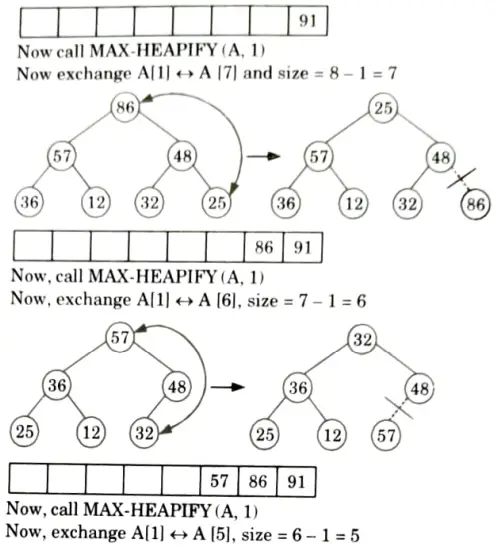
Section 4: Aktu Quantum Pdf of Design and Analysis of Algorithm

a. Discuss the various cases for insertion of key in red-black tree for given sequence of key in an empty red-black tree {15, 13, 12, 16, 19, 23, 5, 8}.

Ans. Insertion: 

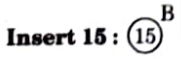
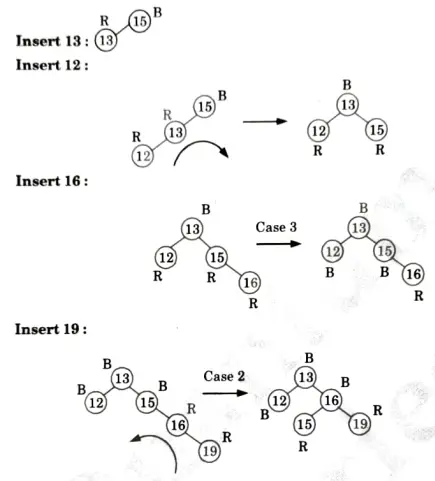
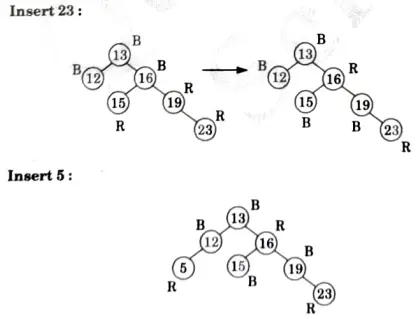
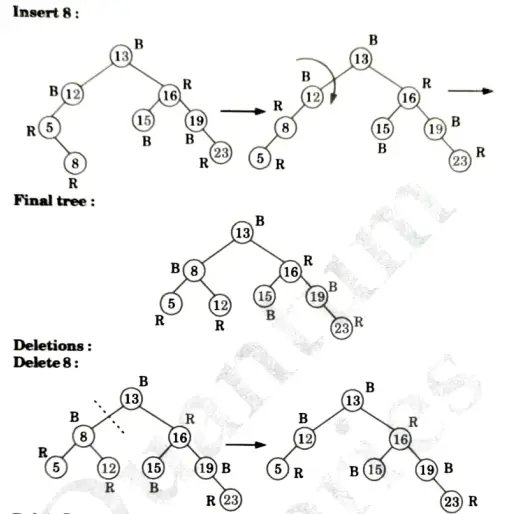
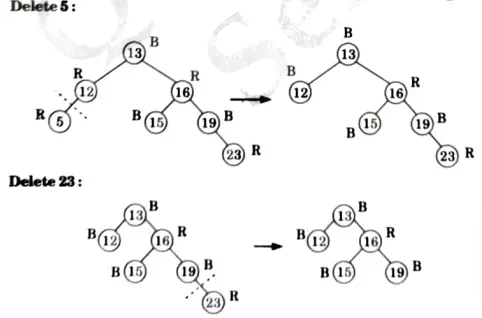
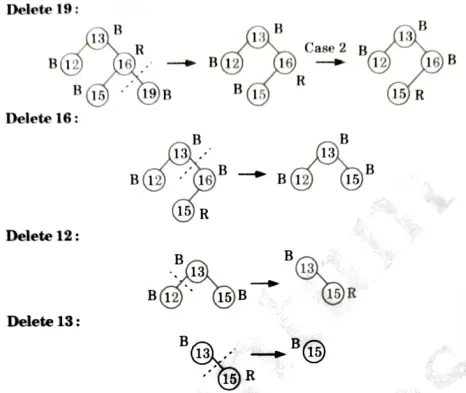
Delete 15: No tree 

b. What is skip list ? Explain the search operation in skip list with suitable example also write its algorithm. 

Ans. Skip list:

• 1. A skip list is built in layers. 
• 2. The bottom layer is an ordinary ordered linked list.
• 3. Each higher layer acts as an “express lane”, where an element in layer i appears in layer (i+ 1) with some fixed probability p (two commonly used values for p are ½  and ¼ .).
• 4. On average, each element appears in 1/(1-p) lists, and the tallest element (usually a special head element at the front of the skip list) in all the lists.
• 5. The skip list contains log_1/p n (i.e., logarithm base 1/p of n). 

Searching operations algorithm:

Example: 

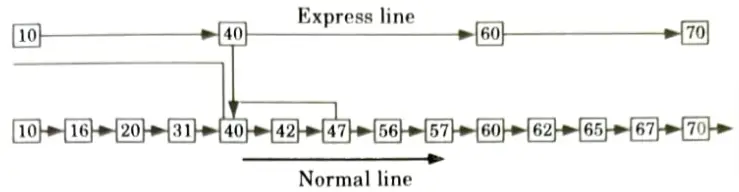
• 1. Let’stake an example to understand the working of the skip list. In this example, we have 14 nodes, such that these nodes are divided into two layers, as shown in the diagram. 
• 2. The lower is a common line that links all nodes, and the top layer is an express line that links only the main nodes, as you can see in the diagram. 
• 3. Suppose you want to find 47 in this example. You will start the search from the first node of the express line and continue running on the express line until you find a node that is equal a 47 or more than 47. 
• 4. You can see in the example that 47 does not exist in the express line, so you search for a node of less than 47, which is 40. Now, you go to the normal line with the help of 40, and search the 47, as shown in the diagram. 

Section 5: Design and Analysis of Algorithm Aktu Solved Question Paper

a. What is Knapsack problem ? Solve Fractional Knapsack problem using greedy programming for the following four items with their weights w = {3,5, 9, 5} and values P = {45, 30, 45, 10} with Knapsack capacity is 16. 

Ans. Knapsack problem:

• 1. The knapsack problem is a problem in combinatorial optimization.
• 2. Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.  

Approach use to solve the problem: 

• 1. In knapsack problem, we have to fill the knapsack of capacity W, with a given set of items I₁, I₂…..I_n having weight w₁, w₂…..w_n in such a manner that the total weight of items cannot exceed the capacity of knapsack and maximum possible value (v) can be obtained. 
• 2. Using branch and bound approach, we have a bound that none of the items can have total sum more than the capacity of knapsack and must give maximum possible value. 
• 3. The implicit tree for this problem is a binary tree in which left branch implies inclusion and right implies exclusion. 
• 4. Upper bound of node can be calculated as:

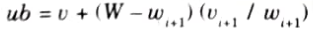
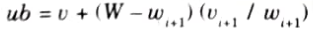
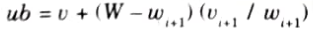
Numerical: 

Given:  

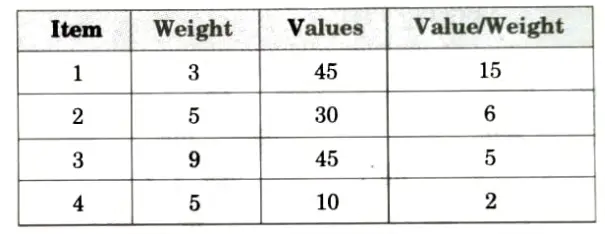
To fulfill capacity W= 16 we will have 

1. Add item of weight 3, W = 16 – 3 = 13 

2. Add item of weight 5, W = 13 – 5 = 8 

3. Skip item of weight 9 

4. Add item of weight 5, W= 8 – 5 = 3 

Total maximum value = 45 + 30 + 10 = 85

b. Write Clown the Bellman Ford algorithm to solve the single source shortest path problem also write its time complexity. 

Ans. Bellman Ford algorithm:  

• 1. Bellman-Ford algorithm finds all shortest path length from a source s 𝜖 V to all u 𝜖 V or determines that a negative-weight cycle exists. 
• 2. Bellman-Ford algorithm solves the single source shortest path problem in the general case in which edges of a given digraph G can have negative weight as long as G contains no negative cycles. 
• 3. This algorithm, uses the notation of edge relaxation but does not use with greedy method. 
• 4. The algorithm returns boolean TRUE if the given digraph contains no negative cycles that are reachable from source vertex otherwise it returns boolean FALSE. 

Bellman-Ford (G, w, s): 

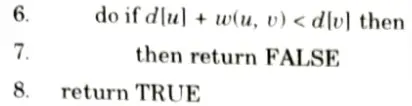
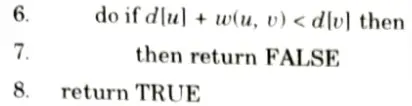
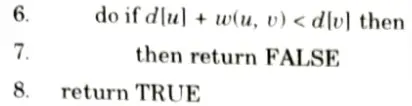
RELAX (u, v, w): 

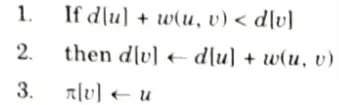
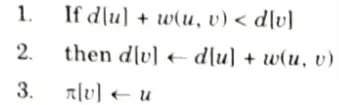
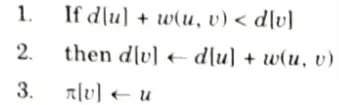
If Bellman-Ford returns true, then G forms a shortest path tree, else there exists a negative weight cycle. 

Time complexity: Time complexity of Bellman-Ford algorithm is OVE), where V is vertex and E is edge of the graph.  

Section 6: Aktu Btech Notes Pdf Design and Analysis of Algorithm

a. What is travelling Salesman Problem (TSP) ? Find the solution of following TSP using branch and bound method. 

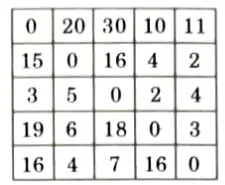
Ans. Travelling Salesman Problem (TSP): Travelling salesman problem is the problem to find the shortest possible route for a given set of cities and distance between the pair of cities that visits every city exactly once and returns to the starting point.

Numerical: 

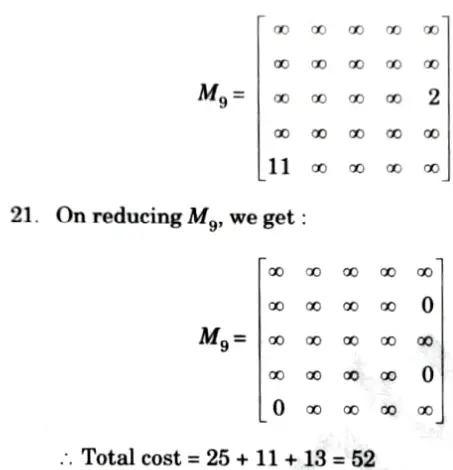
1. Reduce each column and row by reducing the minimum value from each element in row and column. 

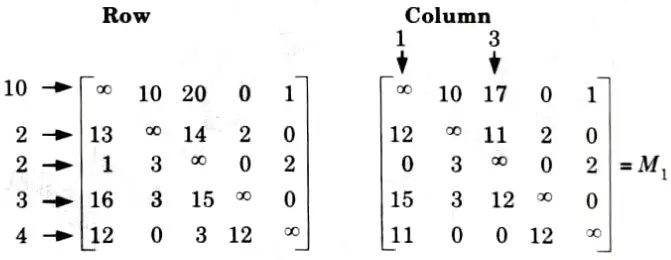
2. So, total expected cost is: 10 + 2 + 2 + 3 + 4 + 1 + 3 = 25. 

3. We have discovered the root node V₁ so the next node to be expanded will be V₂, V₃, V₄, V₅ Obtain cost of expanding using cost matrix for node 2.

4. Change all the elements in 1^st row and 2^nd column.

5. Now, reducing M₂ in rows and columns, we get:   

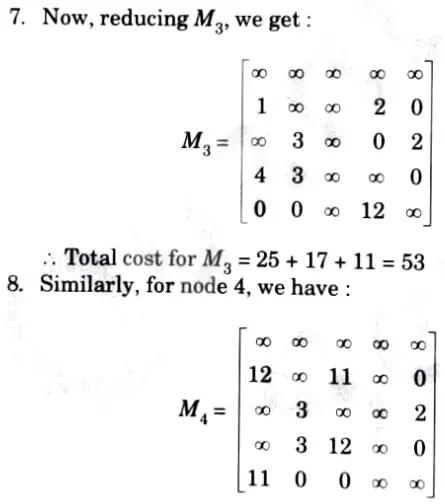
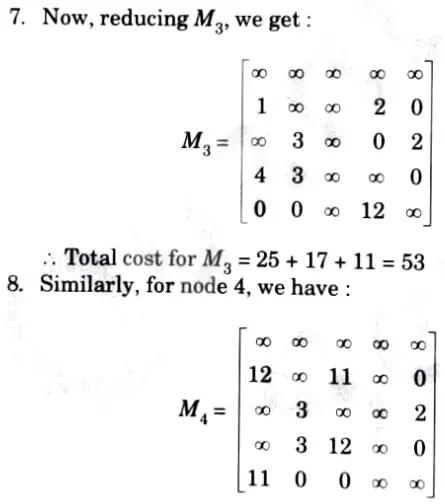
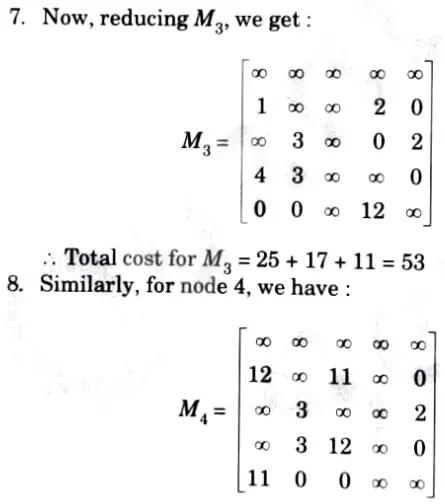
Find the solution of following TSP using branch and bound method. 

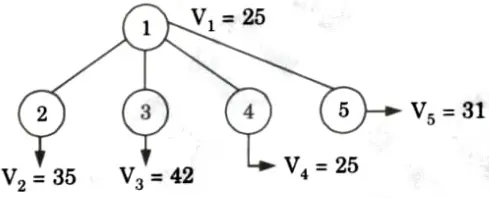
12. Now, the promising node is V₄ = 25. Now, we can expand V₂, V₃, and V₅. Now, the input matrix will be M₄. 

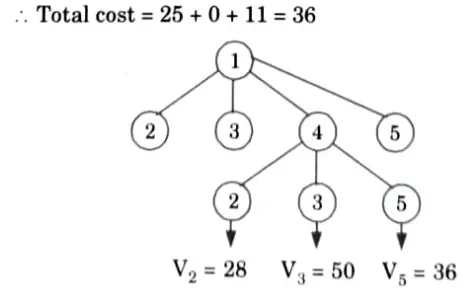
19. Now, promising node is V₂ = 28. Now, we can expand V₁ and V_5. Now, the input matrix will be M₇.

20. Change all the elements in 2^nd row and 3^rd columnn. 

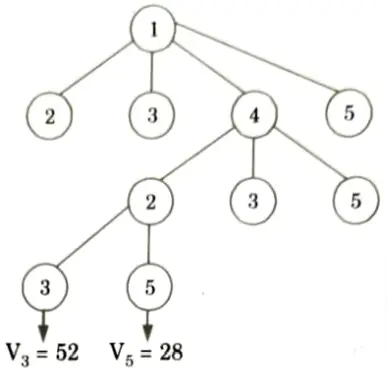
24. Here V₅ is the most promising node so next we are going to expand this node further. Now, we are left with only one node not yet 5. traversed which is V₅.

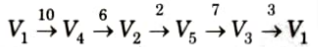
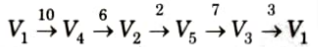
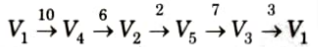
So, total eost of traversing the graph is:

10 + 6  +2 + 7 + 3 = 28 

b. Explain the method of finding Hamiltonian cycles in a graph using backtracking method with suitable example. 

Ans.

• 1. Given a graph G = (V, E), we have to find the Hamiltonian circuit using backtracking approach.
• 2. We start our search from any arbitrary vertex, say ‘a’. This vertex ‘a’ becomes the root of our implicit tree. 
• 3. The first element ofour partial solution is the first intermediate vertex of the Hamiltonian cycle that is to be constructed. 
• 4. The next adjacent vertex is selected on the basis of alphabetical (or numerical) order.  
• 5. If at any stage any arbitrary vertex makes a cycle with any vertex other than vertex ‘a’ then we say that dead end is reached.
• 6. In this case we backtrack one step, and again search begins by selecting another vertex and backtrack the element from the partial solution must be removed. 
• 7. The search using backtracking is successful if a Hamiltonian cycle is obtained. 

Section 7: Design and Analysis of Algorithm Pdf notes of Aktu Quantum

a. Write and explain the algorithm to solve vertex cover problem using approximation algorithm.  

Ans. A vertex cover of an undirected graph G = (V, E) is a subset of V’ ⊆ V such that if edge (u, v) 𝜖 G then u 𝜖 V or v 𝜖 V (or both).  

Problem: Find a vertex cover of maximum size in a given undirected graph. This optimal vertex cover is the optimization version of an NP-Complete problem but it is not too hard to find a vertex cover that is near optimal.  

Approx-vertex-cover (G: Graph)

Analysis: It is easy to see that the running time of this algorithm is O(V+ E), using adjacency list to represent E’.

b. Explain and write the Knuth-Morris-Pratt algorithm for pattern matching also write its time complexity.  

Ans. Knuth-Morris-Pratt algorithm:

COMPUTE-PREFIX-FUNCTION (P)  

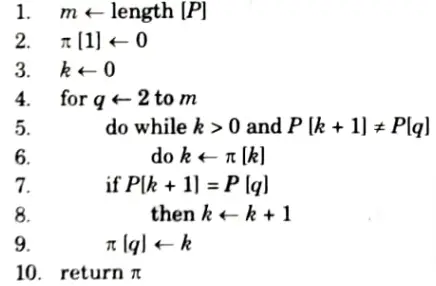
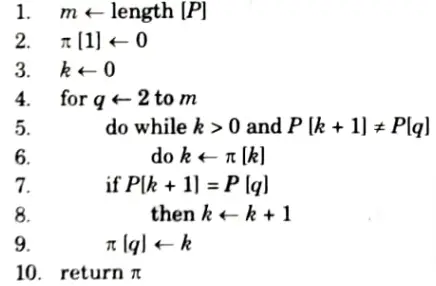
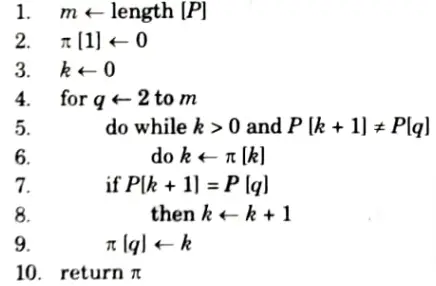
KMP-MATCHER calls the auxiliary procedure COMPUTE-PREFIX-FUNCTION to compute 𝜋.

KMP-MATCHER (T, p)  

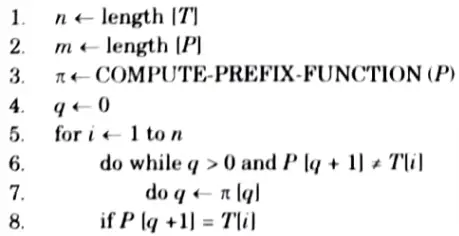
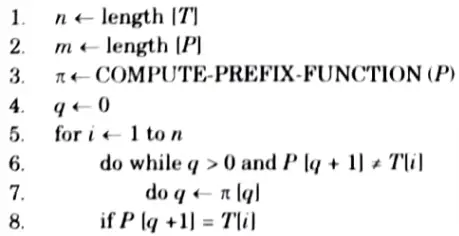
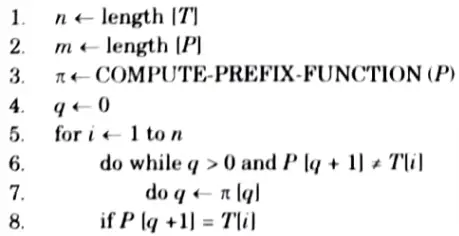
Time complexity: The time complexity of KMP algorithm is O(n) in the worst case.