Utilise Quantum Notes to reveal the techniques of algorithm design and analysis. Utilise important, commonly asked questions to prepare for the Aktu Btech examinations. Do well in your academic endeavours today! Unit-2 Advanced Data Structure
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Design and Analysis of Algorithm: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. Define a red-black tree with its properties. Explain the insertion operation in a red-black tree.
Ans. Red-black tree:
A red-black tree is a binary tree where each node has colour as an extra attribute, either red or black. It is a self-balancing Binary Search Tree (BST) where every node follows following properties:
- 1. Every node is either red or black.
- 2. The root is black.
- 3. Every leaf (NIL) is black.
- 4. If a node is red, then both its children are black.
- 5. For each node, all paths from the node to descendent leave contain the same number of black nodes.
Insertion:
i. We begin by adding the node as we do in a simple binary search tree and colouring it red.
RB-INSERT (T, z)



ii. Now, for any colour violation, RB-INSERT-FIXUP procedure is used.
RB-INSERT-FIXUP (T, z)



Cases of RB-tree for insertion:
Case 1:
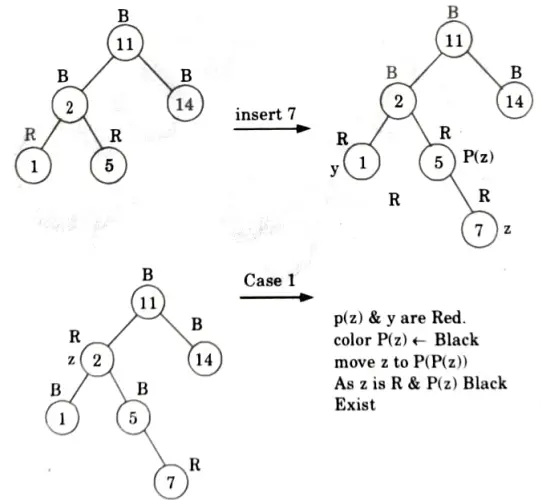


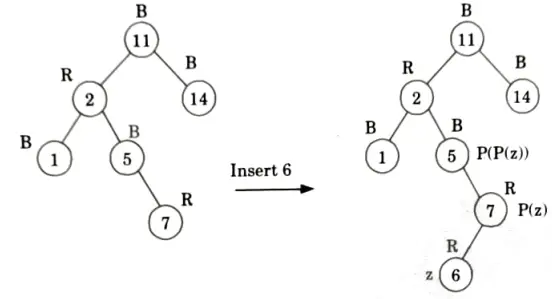


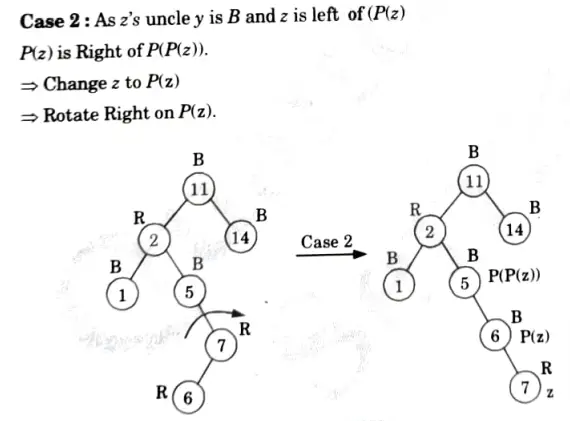





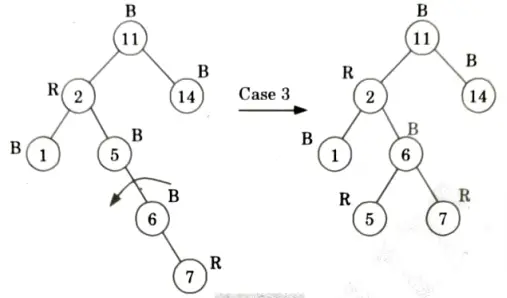


Q2. Insert the nodes 15, 13, 12, 16, 19, 23, 5, 8 in empty red-black tree and delete in the reverse order of insertion.
Ans. Insertion:
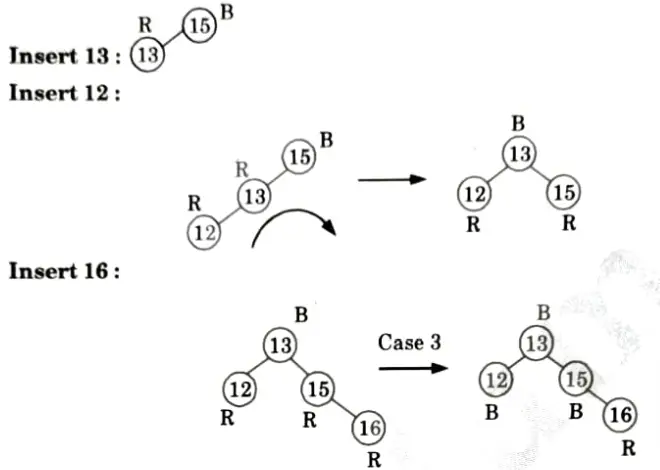


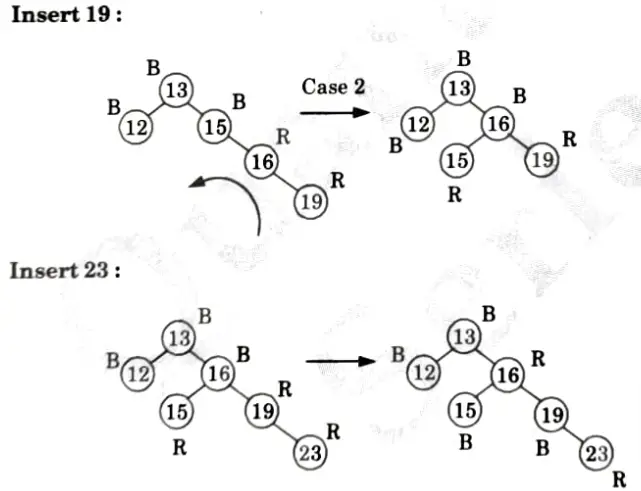


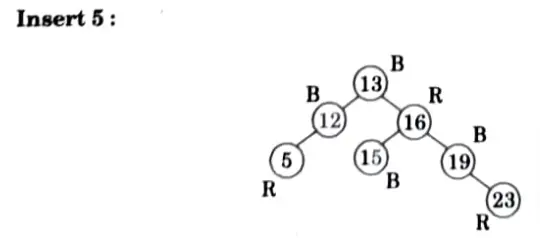


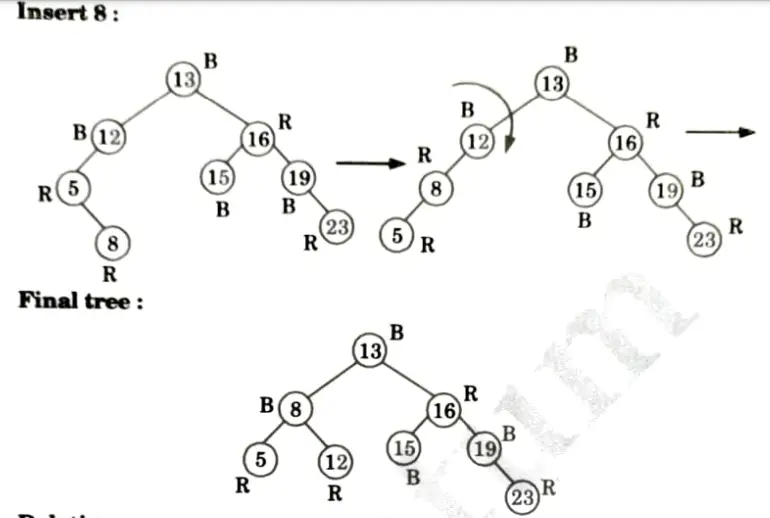


Deletions:
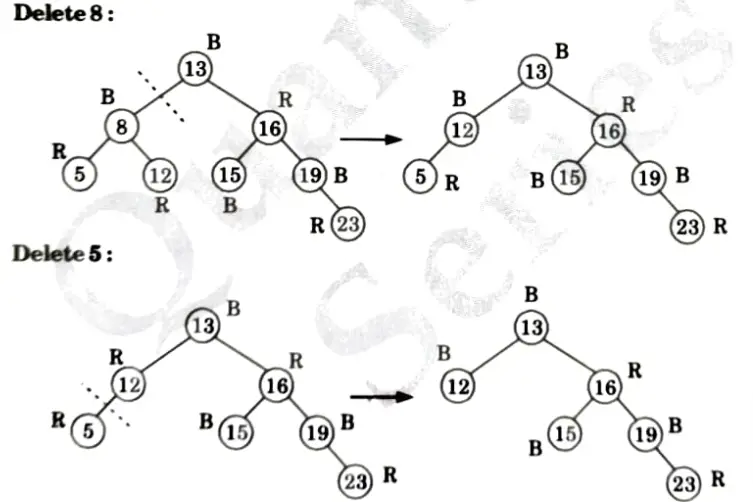


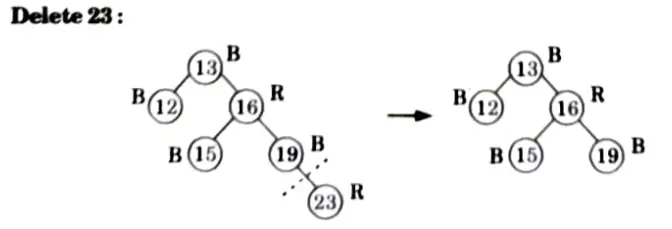


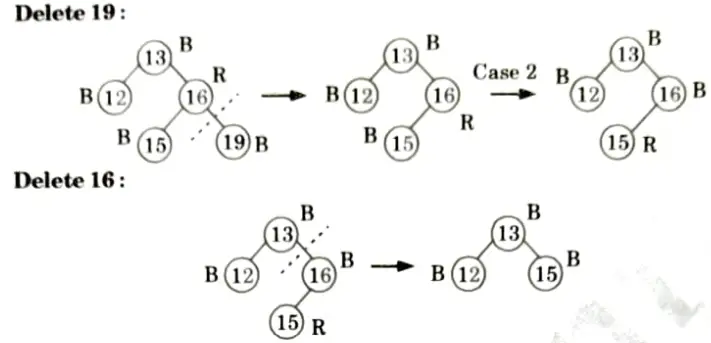


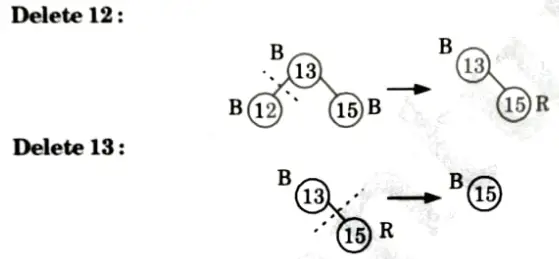


Delete 15:
No tree
Q3. Define a B-tree of order m. Explain the searching and insertion algorithm in a B-tree.
Ans. AB-tree of order m is an m-ary search tree with the following properties:
- 1. The root is either leaf or has atleast two children.
- 2. Each node, except for the root and the leaves, has between m/2 and m children.
- 3. Each path from the root to a leaf has the same length.
- 4. The root, each internal node and each leaf is typically a disk block.
- 5. Each internal node has upto (m – 1) key values and upto m children.
SEARCH (x, k)



B-TREE-INSERT (T, k)



B-TREE SPLIT CHILD (x, i, y)
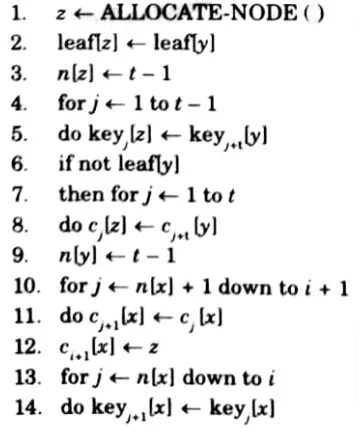
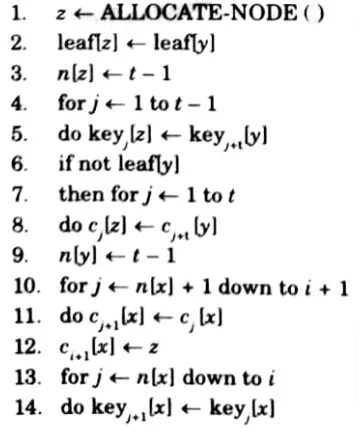
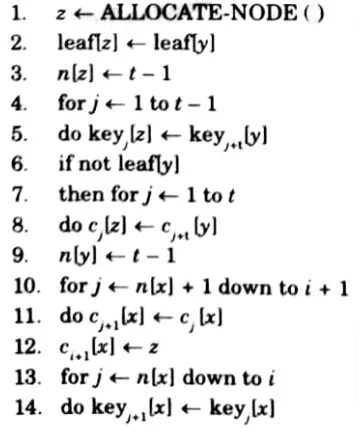



B-TREE-NSERT-NONFULL (x, k)



Q4. What are the characteristics of B-tree ? Write down the steps for insertion operation in B-tree.
Ans. Characteristic of B-tree:
- 1. Each node of the tree, except the root node and leaves has at least m/2 subtrees and no more than m subtrees.
- 2. Root of tree has at least two subtree unless it is a leaf node.
- 3. All leaves of the tree are at same level.
Insertion operation in B-tree:
In a B-tree, the new element must be added only at leaf node. The insertion operation is performed as follows:
- Step 1: Check whether tree is empty.
- Step 2: If tree is empty, then create a new node with new key value and1 insert into the tree as a root node.
- Step 3: If tree is not empty, then find a leaf node to which the new key value can be added using binary search tree logic.
- Step 4: If that leaf node has an empty position, then add the new key value to that leaf node by maintaining ascending order of key value within the node.
- Step 5: If that leaf node is already full, then split that leaf node by sending middle value to its parent node. Repeat the same until sending value is fixed into a node.
- Step 6: If the splitting is occurring to the root node, then the middle value becomes new root node for the tree and the height of the tree is increased by one.
Q5. How B-tree differs with other tree structures ?
Ans.
- 1. In B-tree, the maximum number of child nodes a non-terminal node can have is m where m is the order of the B-tree. On the other hand, other tree can have at most two subtrees or child nodes.
- 2. B-tree is used when data is stored in disk whereas other tree is used when data is stored in fast memory like RAM.
- 3. B-tree is employed in code indexing data structure in DBMS, while, other tree is employed in code optimization, Huffman coding, etc.
- 4. The maximum height of a B-tree is log mn (m is the order of tree and n is the number of nodes) and maximum height of other tree is log, n (base is 2 because it is for binary).
- 5. A binary tree is allowed to have zero nodes whereas any other tree must have atleast one node. Thus binary tree is really a different kind of object than any other tree.
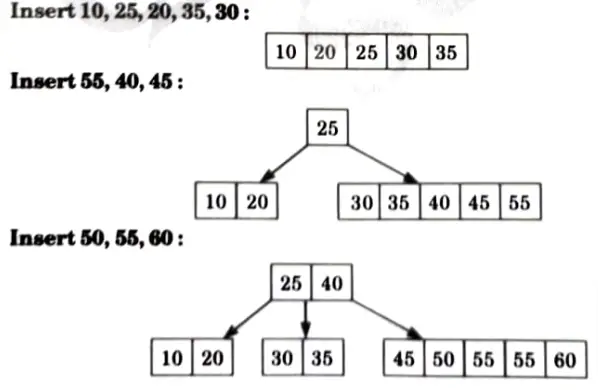
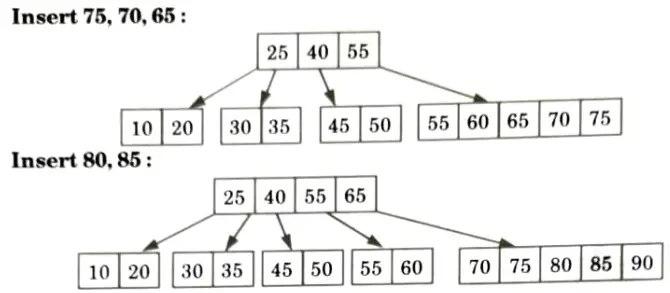
Q6. Using minimum degree f’ as 3, insert following sequence of integers 10, 25, 20, 35, 30, 55, 40, 45, 50, 55, 60, 75, 70, 6, 80, 85 and 90 in an initially empty B-Tree. Give the number of nodes splitting operations that take place.
Ans. Using minimum degree t = 3, insert 10, 25, 20, 35, 30, 55, 40, 45, 50, 55, 60, 75, 70, 65, 80, 85 and 90.
Maximum number of key, s = 2t -1 = 2 x 3 – 1 = 5
Minimum number of key, t – 1 = 3 – 1 = 2







Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Design and Analysis of Algorithm Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Design and Analysis of Algorithm Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
