With Quantum Notes, discover the techniques for designing and analysing algorithms. Useful, often asked questions will help you prepare for the Aktu Btech exams. Do well in your current academic career! Unit-1 Introduction
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Design and Analysis of Algorithm: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. What do you mean by analysis or complexity of an algorithm ? Give its types and cases.
Ans. Analysis/complexity of an algorithm:
The complexity of an algorithm is a function g(n) that gives the upper bound of the number of operation (or running time) performed by an algorithm when the input size is n.
Types of complexity:
Space complexity: Space complexity of an algorithm is the amount of memory it needs to run to complection, including the space for input values for execution.
Time complexity: Time complexity of an algorithm is the number of times a statement executes. It is not the actual time required to execute a particular code.
Cases of complexity:
- 1. Worst case: It is the upper bound on the running time of an algorithm. It is the case that causes a maximum number of operation to be executed.
- 2. Average case complexity: The running time for any given size input will be the average number of operations over all problem instances for a given size.
- 3. Best case complexity: The best case complexity of the algorithm is the function defined by the minimum number of steps taken on any instance of size n.
Q2. What do you mean by recursion ? Explain your answer with an example.
Ans.
- 1. Recursion is a process of expressing a function that calls itself to perform specific operation.
- 2. Indirect recursion occurs when one function calls another function that then calls the first function.
- 3. Suppose P is a procedure containing either a call statement to itself or a call statement to a second procedure that may eventually result in a call statement back to the original procedure P. Then P is called recursive procedure.
- 4. A recursive procedure must have the following two properties:
- a. There must be certain criteria, called base criteria, for which the procedure does not call itself.
- b. Each time the procedure does call itself, it must be closer to the criteria.
- 5. A recursive procedure with these two properties is said to be well defined.
For example:
The factorial function may also be defined as follows:
a. If n 0, then n! = 1.
Here, the value of n! is explicitly given when n = 0 (thus 0 is the base value).
b. Ifn >0, then n! = n. (n – 1)!
Here, the value of n! for arbitrary n is defined in terms of a smaller value of n which is closer to the base value 0.
Observe that this definition of n! is recursive, since it refers to itself when it uses (n- 1)!
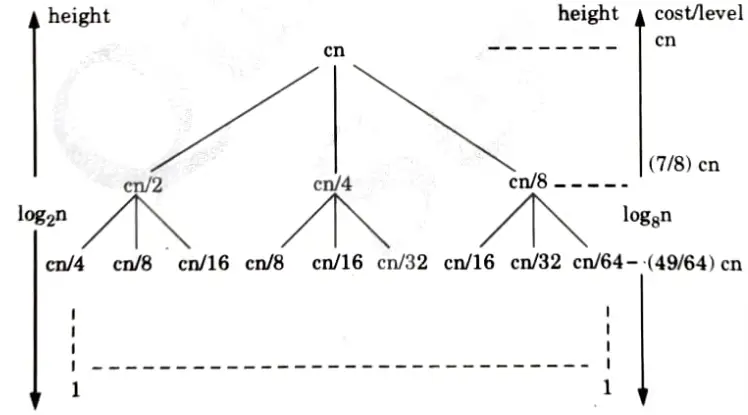
Q3. Solve the following recurrences:
T(n) = T(n/2) + T(n/4)+ T(n/8) + n
Ans.








Q4. Write non-deterministie algorithm for sorting.
Ans.
- 1. A non-deterministic algorithm gives different outputs for the same input on different executions.
- 2. A sorting algorithm will give same output on same input on every occanion if all the elements in the input array are distinct.
- 3. However, if the input array contain duplicate elements, then any unstable sorting algorithm will behave non-deterministically. Example: Quick sort, Heap sort and Selection sort.
N SORT(A, B):
- 1. for i = 1 to n do
- 2. j = choice(1… n)
- 3. if BUl! = 0 then failure
- 4. B[j] = A[i]
- 5. endfor
- 6. for i = 1 to n -1 do
- 7. if B[i]< B [i + 1] then failure
- 8. endfor
- 9. print(B)
- 10. success
Q5. How will you sort following array A of element using heap sort:
A (23, 9, 18, 45, 5, 9, 1, 17, 6).
Ans.
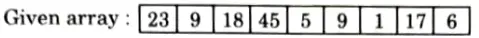
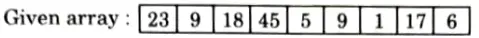
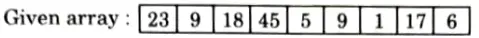
First we call Build-Max heap
heap size [A] =9
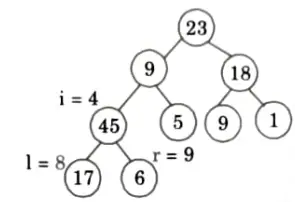


so i = 4 to 1 call MAX HEAPIFY (A, i)
ie., first we call MAX HEAPIFY (A, 4)



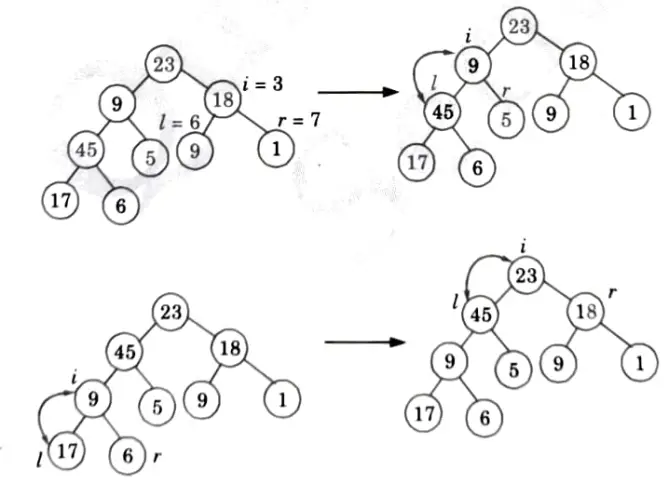
Similarly for i = 3, 2, 1 we get the following heap tree:


So, final tree after Build-Max heap is
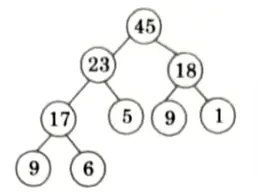


Now i = 9 down to 2 and size = size -1 and call MAX HEAPIFY (A, 1) each time.
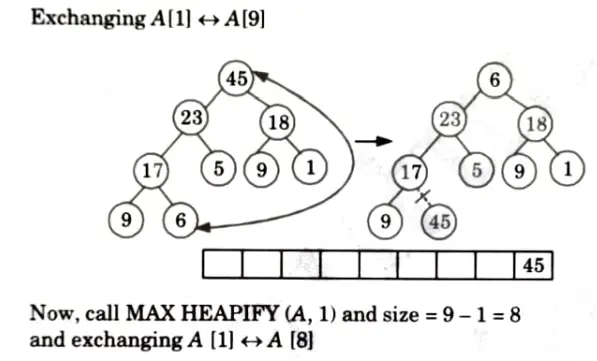


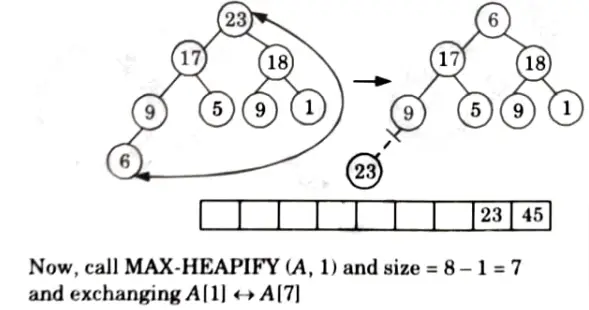


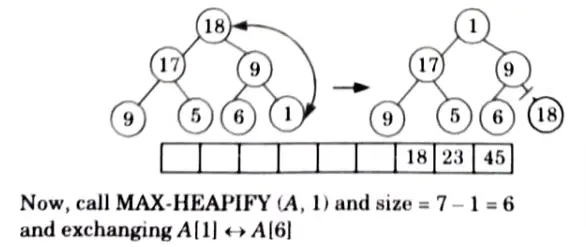


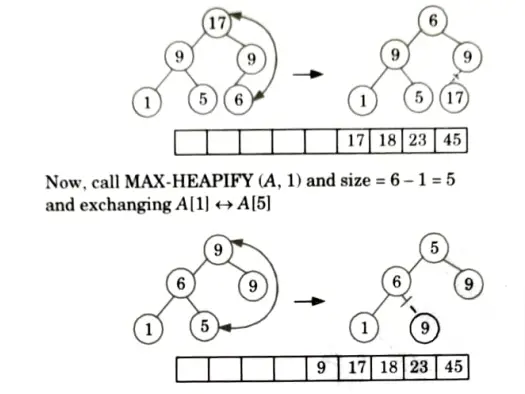


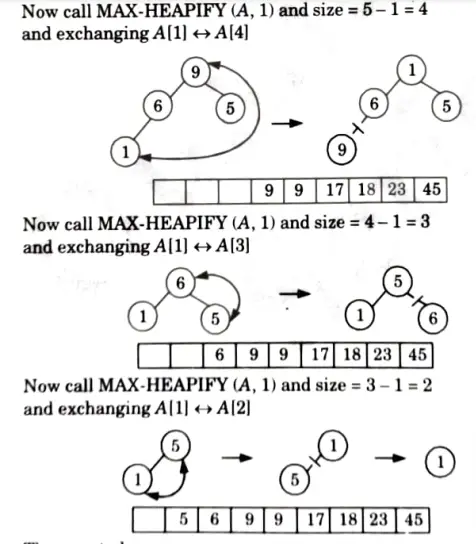


Thus, sorted array:



Q6. Write the bucket sort algorithm.
Ans.
- 1. The bucket sort is used to divide the interval [0, 1] into n equal-sized sub-intervals, or bucket, and then distribute the n-input numbers into the bucket.
- 2. Since the inputs are uniformly distributed over [0, 1], we do not except many numbers to fall into each bucket.
- 3. To produce the output, simply sort the numbers in each bucket and then go through the bucket in order, listing the elements in each.
- 3. The code assumes that input is in n-element array A and each element in A satisfies 0 ≤ A[i] ≤ 1. We also need an auxiliary array B[0.. n – 1] for linked-list (buckets).
BUCKET_SORT (A)






Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Design and Analysis of Algorithm Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Design and Analysis of Algorithm Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
