Unit 3 of Fluid Mechanics addresses POTENTIAL FLOW, which is an important topic in understanding fluid dynamics. This section covers the Laplace equation, Bernoulli’s equation, velocity potential, and stream function, as well as its applications. The main questions in this lesson will assess students’ comprehension of these concepts as well as their ability to apply them in problem-solving settings.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Fluid Mechanics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Q1. What do you understand by the term ideal fluid flow or potential flow ? Discuss its importance.
Ans. A. Potential Flow or Ideal Fluid Flow:
- 1. It refers to an incompressible and inviscid flow, ie. ρ = constant and μ =0
- 2. As viscosity is zero, i.e., there cannot be any shear stresses in a potential flow. Hence,
- a. The only stress at a point in an ideal fluid flow must be the pressure.
- b. The only stress the fluid may act on the solid boundary must be normal to it at that point.
- 3. An ideal fluid flow may be steady or unsteady and uniform or non-uniform.
B. Importance of Ideal Fluid Flow or Potential Flow:
- 1. An engineer works with many sorts of flows in a variety of contexts, such as flow through limited spaces, fluid machines, control systems, etc.
- 2. In practise, the flow may be complicated as a result of phenomena like boundary layers, separation, recirculation, etc., making it challenging to analyse the flow precisely. The straightforward method of ideal fluid flow analysis therefore acquires significant importance in engineering.
Q2. Write short note on source, sink and doublet.
Ans. A. Source:
1. It is a point from which flow is moving radially in all directions of a plane at uniform rate.
B. Sink:
1. It is a point in which fluid moves radially inwards and it disappears at a constant rate.
C. Doublet:
1. When a source and sink pair approach each other in such a way that the distance 2a between them approaches zero and the product 2a, it is a specific instance of a source and sink pair (both of them are of equal strength, q). q is unchanging.
2. This product 2a. q is known as doublet strength and is denoted by μ.
∴ Doublet strength, μ = 2a.q
Q3. Derive Euler’s equation of motion.
Ans. 1. As shown in Fig., consider a stream-line in which flow is taking place in S-direction.
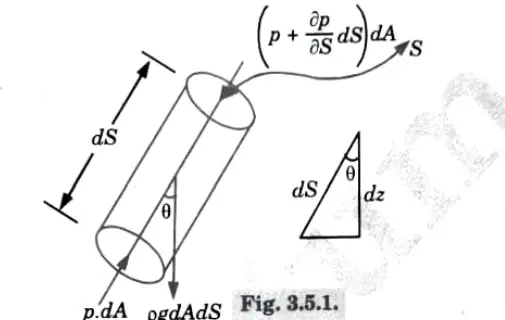


- 2. Consider a cylindrical element of cross section dA, length dS and Let 0 is the angle between the direction of flow and the line of action of the weight of element.
- 3. The forces acting on the cylindrical elements are:
- a. Pressure force pdA in the direction of flow
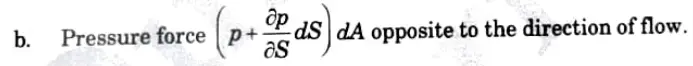
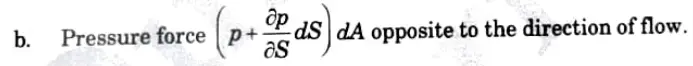
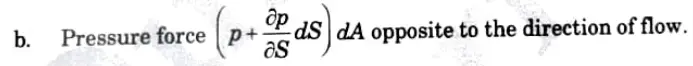
c.Weight of element pe dA ds.
4. For equilibrium,



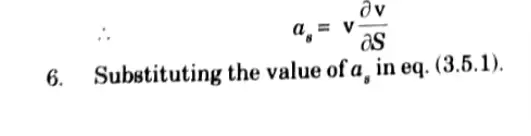
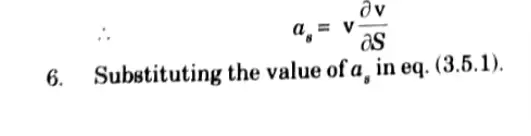
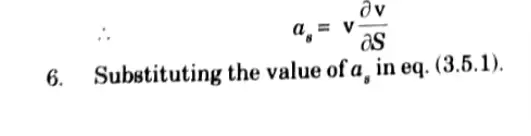



The eq. (3.5.4) is known as Euler’s equation of motion.
Q4. Find the discharge from an 80 mm diameter external mouth piece fitted to a side of a large vessel if the head over the mouthpiece is 6 m.
Ans. Given: d= 80 mm 0.08 m, H = 6m
To Find: Discharge
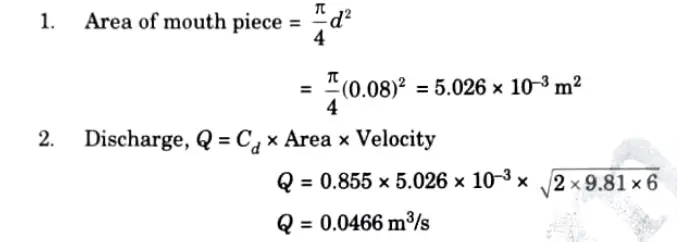
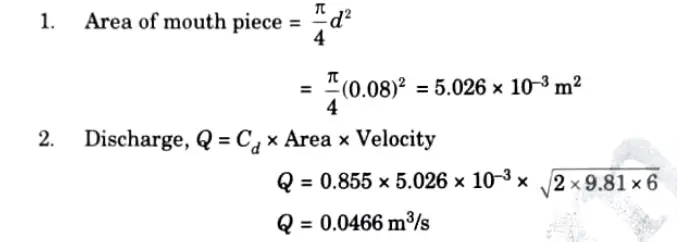
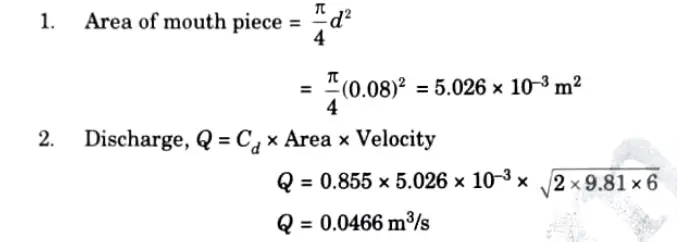
Q5. Apipe tapers from 250 mm to 125 mm; the rate of flow of the liquid in the pipe is 24000 lit/min. Calculate average velocity of flow at two sections.
Ans. Given:Q 24000 I/min= 0.4 m3/sec d1 =250 mm=0.25 m, d2 125 mm =0.125 m
To Find: Average velocity of flow at two sections.



Q6. Define weir and give its classification.
Ans. A. Weir:
1. It is any regular obstruction in an open stream over which the flow takes place.
B. Classification of Weirs:
- a. On the Basis of Shape
- 1. Rectangular weir, and
- 2. Cipoletti weir.
- b. On the Basis of Nature of Discharge:
- 1. Ordinary weir, and
- 2 Submerged weir
- c. On the Basis of the Width of Crest :
- 1. Narrow crested, and
- 2. Broad crested.
- d According to the Nature of Crest:
- 1. Sharp crested weir, and
- 2. Ogee weir.
- e. On the Basis of the Effect of Sides on the Emerging Nappe:
- 1. Weir with end contraction, and
- 2. Weir without end contraction.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Fluid Mechanics Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Fluid Mechanics Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
