Discover AKTU B.Tech Quantum Book Short Question Notes on Information Theory and Coding. Discover the principles of data compression, error correction, and efficient information transmission.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Information Theory and Coding: *Quantum *B.tech-Syllabus *Circulars *B.tech AKTU RESULT * Btech 4th Year * Aktu Solved Question Paper
Unit-I: Entropy, Relative Entropy and Mutual Information (Short Question)
Q1. What is entropy ? Write its formula.
Ans. Entropy is measured in terms of the probabilistic behaviour of the source of information.
Entropy is calculated by formula
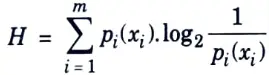
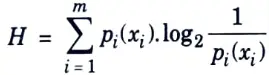
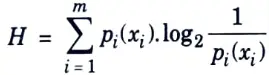
Q2. Describe the probability mass function.
Ans. The relative entropy D (p || g) of the probability mass function p w.r.t. the probability mass function of q is defined by
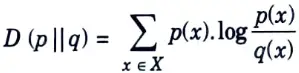
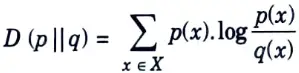
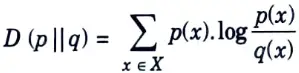
Q3. What do you mean by mutual information ?
Ans. Mutual information is defined as
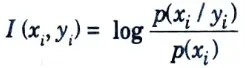
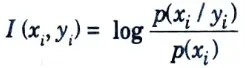
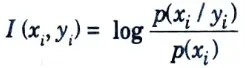
Q4. State the chain rule for various operations.
Ans. Chain rules:
Entropy:
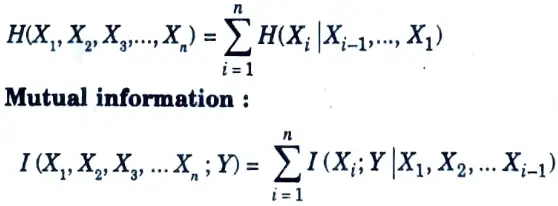
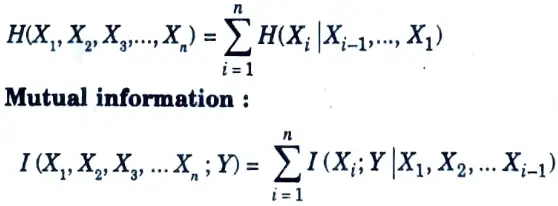
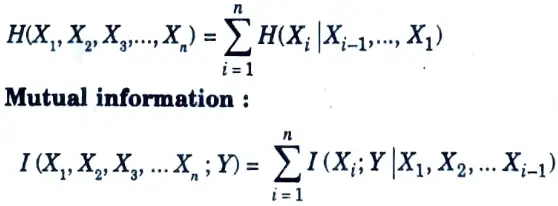
Relative entropy:
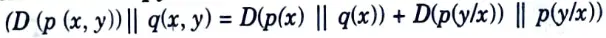
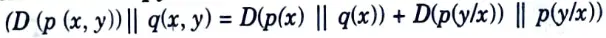
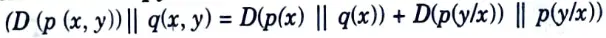
Q5. Explain joint entropy.
Ans. The joint entropy H(X, Y) of a pair of discrete random variables (X, Y) with a joint distribution p(x, y) is defined as
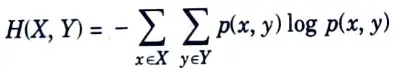
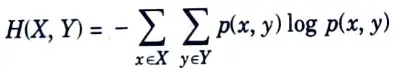
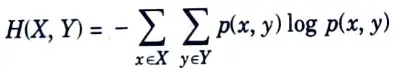
which can also be expressed as
H(X, Y) = -E log p(X, Y)
Q6. What is conditional entropy ?
Ans.
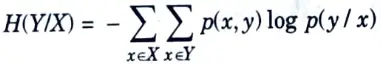
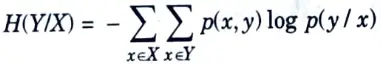
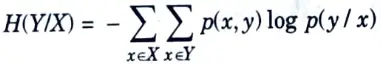
Q7. What do you mean by relative entropy ?
Ans. he relative entropy is a measure of the distance between two distributions. The relative entropy or Kullback-Leibler distance between two probability mass functions p (x) and g(x) is defined as
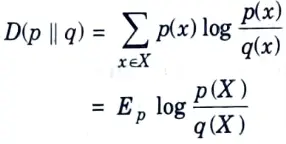
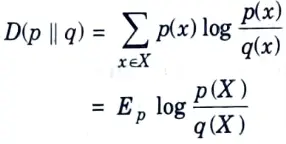
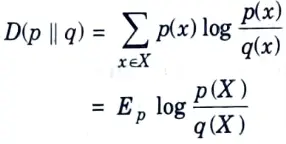
Q8. Explain Jensen’s inequality in brief.
Ans. If ‘f’ is a convex function, then Ef (x) ≥ f(Ex).
Q9. What are the impact of convex and concave function ?
Ans.



A function f is concave if -f is convex.
A function is concave if it always lies above any chord.
Q10. State log sum inequality.
Ans.
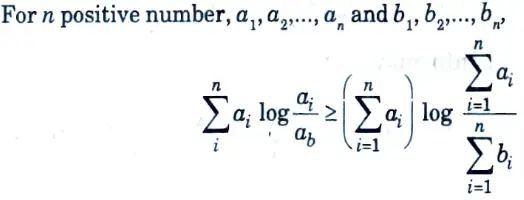
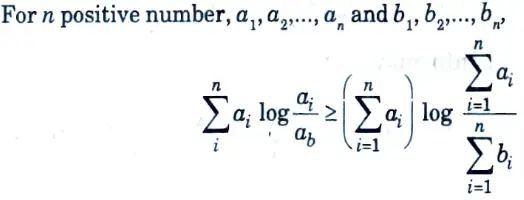
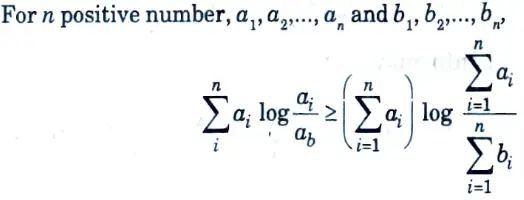
Q11. State the concept of data processing inequality.
Ans. If x → y → z forms a Markov chain, then
I (X; ) ≥ I (X; Z)
Q12. Describe sufficient statistics in short.
Ans. A function T(X) is said to be a sufficient statistic relative to the family {f𝛉 (x)} ifX is independent of 𝛉 given T(X) for any distribution on 𝛉 [i.e., 𝛉 → T (X) → X forms a Markov chain).
This is the same as the condition for equality in the data-processing inequality
I (𝛉 ; X) = I (𝛉; T(X))
for all distributions on 𝛉. Hence, sufficient statistics preserve mutual information and conversely.
Q13. Explain Fano’s inequality for pair of random variable.
Ans. Fano’s inequality relates the probability of error in guessing the random variable X to its conditional entropy H(X|Y).
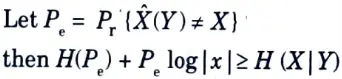
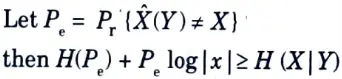
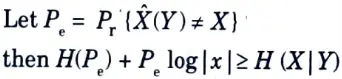
Unit-II: Asymptotic Equipartition Property (Short Question)
Q1. What do you mean by asymptotic equipartition property ?
Ans. The asymptotic equipartition property is the information theory equivalent of the law of large numbers. It is a direct result of the ineffective law of huge numbers.
Q2. What is the law of large numbers ?
Ans. The law of large numbers states that for independent, identically distributed (i.i.d) random variables,
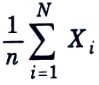
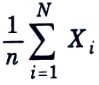
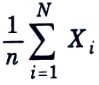
is close to its expected value EX for large values of n.
Q3. Give kraft inequality for instantaneous codes.
Ans.
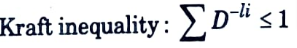
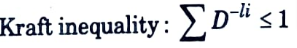
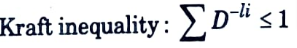
Q4. Write entropy bound on data compression.
Ans. Entropy bound on data compression:
Q5. Define Hufman code.
Ans. 1. Huffman coding provides lowest average codeword length.
2. Huffman coding is variable length source coding method.
Huffman code:
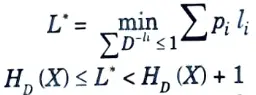
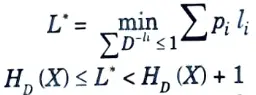
A code is optimal if ∑pili is minimal.
Q6. Define Shannon code.
Ans. Shannon code:
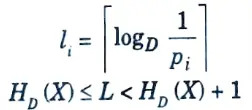
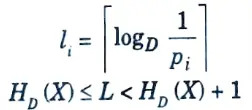
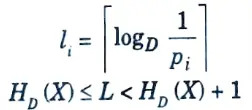
Q7. Give any two properties of Lemma for optimal code.
Ans. The lengths are ordered inversely with the probabilities (i.e, if P, > Pk, then lj ≤ lk).
The two longest codewords have the same length.
Q8. What is the size of the smallest probable set ?
Ans. The size of the smallest “probable” set is about 2n H.
Unit-III: Channel Capacity (Short Question)
Q1. What do you mean by channel capacity ?
Ans. The channel capacity of the discrete memoryless channel is given as maximum average mutual information,
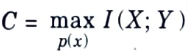
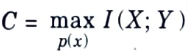
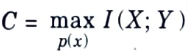
Q2. What is the information capacity of Binary symmetric channel?
Ans. Information capacity of binary symmetric channel is given by
C = 1 – H(P)
Q3. What do you understand by binary erasure channel ?
Ans. In binary erasure channel, a fraction a of the bits are erased. The receiver knows which bits have been erased. The capacity of binary erasure channel is given by
C = 1 – 𝛂
Q4. Give any two properties of channel capacity.
Ans.



Q5. State joint AEP theorem.
Ans. Let (Xn, Yn) be sequences of length n drawn i.i.d. according to
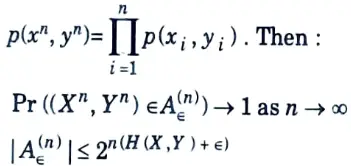
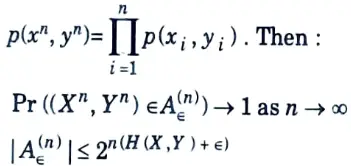
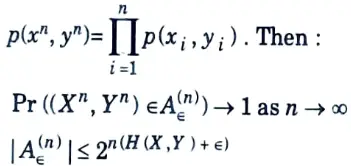
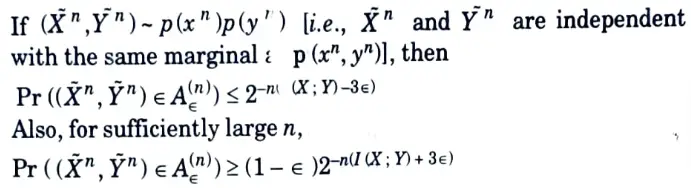
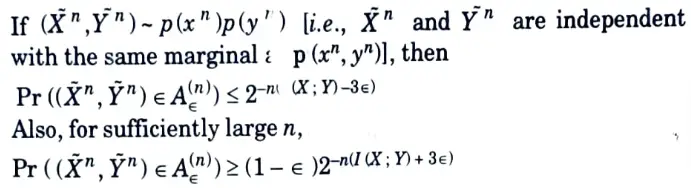
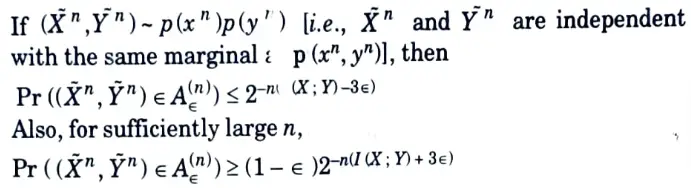
Q6. What is the rate R of an (M, n) code ?
Ans.
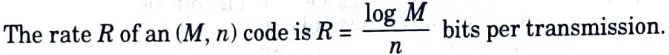
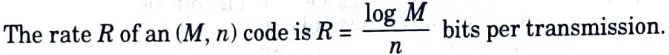
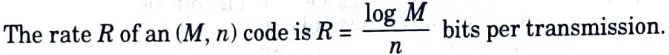
Q7. Define rate of information.
Ans. If the time rate at which source X emits symbols is r (symbols /s), then the information rate R of the source is given by
R = rH(X) b/s
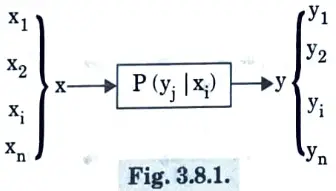
Q8. What do you mean by DMC ?
Ans. DMC (discrete memoryless channel) is a model that has an input X and an output Y. During each signalling period, the channel accepts an input signal from X and generates a symbol from Y in response. When the present output is determined solely by the current input and not by past input, it is said to be memoryless. Representation of DMC is shown in Fig. 3.8.1.


Q9. Define lossless channel with an example.
Ans. A lossless channel is one that is defined by a channel matrix with only one non-zero element in each column.
For example:



In lossless channel no source information is lost in transmission.
Q10. Define deterministic channel with example.
Ans. A deterministic channel is one that is defined by a channel matrix with only one non-zero element in each row.
For example:
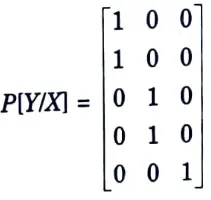
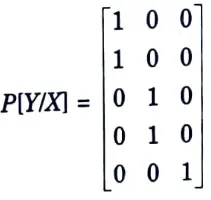
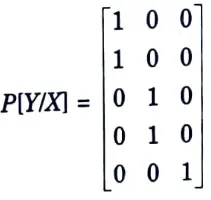
Q11. Define noiseless channel.
Ans. If a channel is both lossless and deterministic, it is said to be noiseless. In each row and column of the channel matrix, there is just one element, which is unity.
For this channel, the input and output alphabets are of same size i.e., m = n.
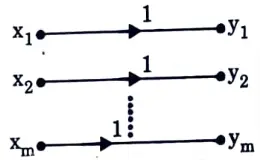


Q12. What do you mean by binary symmetric channel ?
Ans. The binary symmetric channel (BSC) matrix is given by
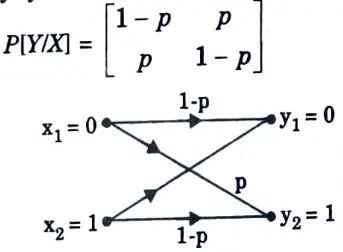


This channel has two inputs (x1 =0, x2 = 1) and two output (y1 = 0, y2 = 1). It is said to be symmetric because the probability of receiving 1 if 0 is sent is same as the probability of receiving 0 if 1 is sent.
Q13. What do you mean by channel capacity per second ?
Ans. When one symbol (digit) is transmitted, the channel capacity provides the maximum amount of information that can be transmitted. If K symbols are transmitted every second, the maximum rate of information transmission per second is KCs. This is the capacity of the channel in information units per second, indicated by C (bits per second).
C = KCs
Q14. A channel is described by a channel matrix with only one non-zero element in each column, Identify the channel.
Ans. Lossless channel.
Q15. A channel is described by a channel matrix with only one non-zero element in each row. Identify the channel.
Ans. Deterministic channel.
Q16. A channel matrix has only one element in each row and in each column and this element is unity. Identify the type of channel.
Ans. Noiseless channel.
Unit-IV: Block Codes and Linear Codes (Short Question)
Q1. Draw the block diagram of digital communication system.
Ans.
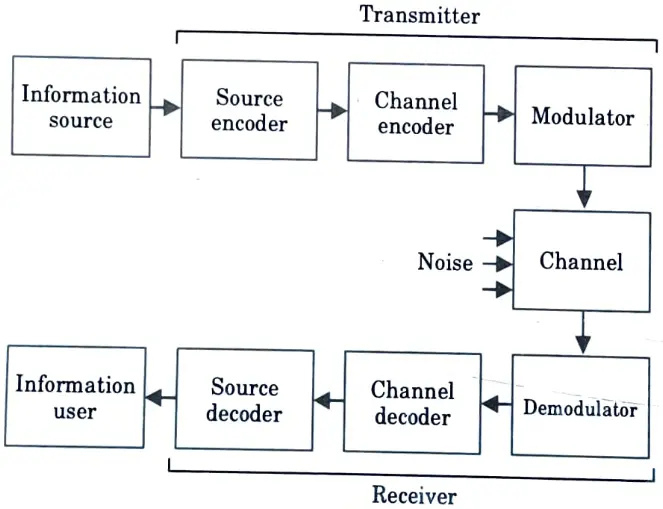


Q2. Define block code.
Ans. In a block code, the encoder’s block of n code digits in a given time unit is determined only by the block of k input data digits within that time unit.
Q3. Define code rate.
Ans. The ratio of the amount of information bits to the block length is a helpful measure of redundancy inside a block code.
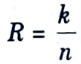
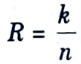
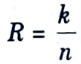
and is known as the code rate.
Q4. Explain parity check codes with the help of example.
Ans. When the number of check bits is one, the simplest possible block code is produced. These are referred to as parity check codes. It is an even parity check code when the check bit is such that the total number of 1’s in the codeword is even, and it is an odd parity check code when the check bit is such that the total number of 1’s in the codeword is odd.
Example:



Q5. Given the (5, 4) even parity block code. Find the codewords corresponding to i1 = (1011) and i2 = (01010)
Ans.
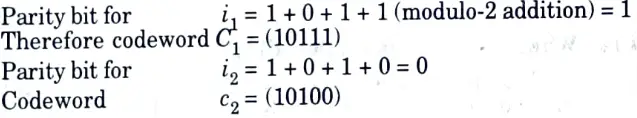
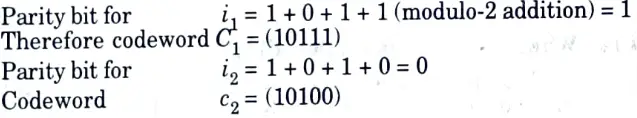
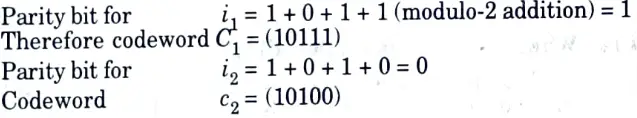
Q6. Given the (8, 7) even parity code. Determine whether v1 = (10110110) and v2 = (01101001) give parity check failures or not.
Ans. The parity check sum for v1 is
s1 = 1 + 0 + 1 + 1 + 0 + 11 + 0 = 1
(module-2 addition)
and so v1 gives a parity check failure.
The parity check sum for v2 is
s2 = 0 + 1 + 1 + 0 + 1 + 0 + 0 + 1 = 0
and so v2 gives the correct parity check sum for an even parity code.
Q7. Calculate error syndrome s if no error occur in the required word v (0111010).
Ans. The parity check sums
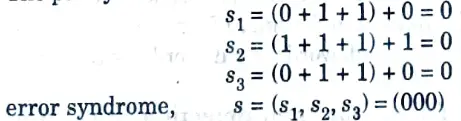
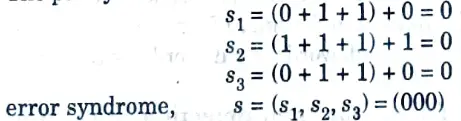
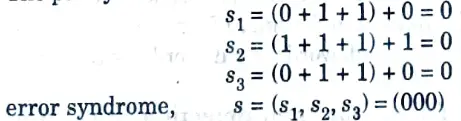
Q8. What is the use of product code ?
Ans. A product code is used to merge two block codes into one more powerful code. Every code bit in a product code is bound by two sets of parities, one from each of the two codes.
Q9. Define repetition codes.
Ans. Repetition codes are block codes in which a single message bit is encoded into a block of identical n bit producing an (n, 1) block code.
Q10. What do you mean by linear block code ?
Ans. If each of the 2k codewords of a systematic code can be expressed as linear combinations of k linearly independent code-vectors, the code is called a linear block code.
Q11. What are the two steps in the encoding procedure for linear block code ?
Ans. 1. The information sequence is divided into message blocks of k information bits each.
2. An encoder transforms each message block into a larger block of n bits using a predefined set of rules.
Q12. What is soft-decision decoding ?
Ans. When the demodulator input is so noisy that a 0 and 1 are interchangeable, a soft choice is taken. Soft-decision decoding is the combination of error control coding and soft-decision demodulation.
Q13. What do you understand by automatic repeat request ?
Ans. When the receiver detects an error, it can request retransmission. This mechanism is known as automatic-repeat-request (ARQ).
Q14. Give the types of ARQ schemes.
Ans. 1. Stop-and-wait ARQ scheme.
2. Go-back-N ARQ scheme.
3. Selective repeat ARQ scheme.
Q15. Define linear codes.
Ans. A block code is considered to be a linear code if its codewords satisfy the requirement that the sum of any two codewords yields another codeword. The weight of the smallest non-zero codeword (or codewords) in a linear code determines the minimum distance.
Q16. Explain the factors for error detection and correction.
Ans. Hamming distance: The hamming distance d(ci, cj) between two codes vectors ci and cj (having the same number of elements) is defined as the number of positions in which their element differ.
Minimum distance: The minimum distance dmin of a linear block code is defined as the smallest hamming distance between any pair of code vector in the code.
Error detection and correction capabilities: The minimum distance dmin of a linear block code is an important parameter of the code. It determines the error detection and correction capabilities of the code.
Q17. Consider the following code vectors :
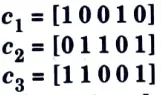
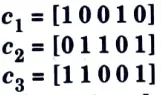
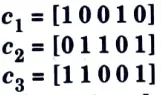
a. Find d(1, c2), d(c1, c3) and d(c2, c3).
b. Show that d(c1, c2) + d(c2, c3) ≥ d(c1, c3).
Ans. a. Since, the hamming distance can be written in terms of hamming weight as,
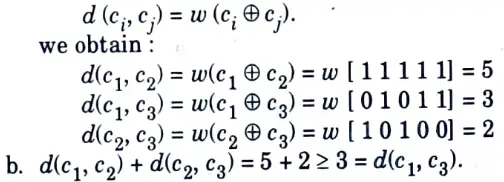
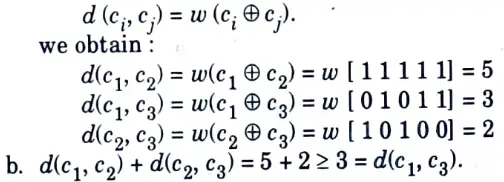
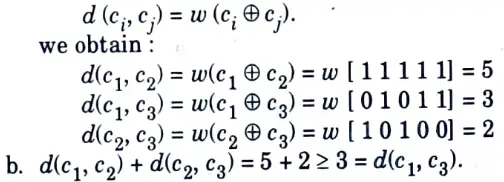
Q18. State the theorem which determines the error detection and correction capabilities of the code.
Ans. An (n, k) linear block code of minimum distance dmin Can correct upto t errors if and only if,
dmin ≥ 2t + 1.
Q19. Define standard array for an (n, k) code.
Ans. For an (n, k) code the standard array consists of all 2n n-bit words and the array is constructed such that for an n-bit word v the array gives the codeword that is the least distance away from v.
Q20. Define error syndrome of a codeword.
Ans. The error syndrome s of a codeword v is defined as:
s = uHT
Q21. What is error control coding ?
Ans. When symbols are received in error, which error control coding is utilised to detect and correct them? This method allows for reliable communication over noisy channels.
Q22. Write the application of error control coding.
Ans. 1. Communication systems for aerospace applications.
2. In mobile (GSM) cellular telephony.
3. Enhancing security in banking and barcode readers.
Q23. What are the types of errors control code ?
Ans. Types of error control code:
1. Block code: A block of n-digits created by the encoder in a given time unit is solely determined by a block of k input message digits inside that time unit.
2. Convolutional code: A block of n code digits generated by the digits encoder inside a time unit depends not only on the block of k message that time unit, but also on the preceding (N – 1) blocks of messages (N > 1).
Q24. What do you understand by shortened linear code ?
Ans. An (n, k) linear code can be shortened to an (n – i, k – i) shortened linear code by setting the first (left hand side) i information bits to zero.
Q25. What do you understand by extended linear code ?
Ans. An (n, k) linear code can be extended to an (n +1, k) extended linear code by adding an overall parity check bit.
Unit-V: Convolution Codes (Short Question)
Q1. Define convolution codes.
Ans. The coded sequence of n digits in convolutional codes is determined not only by the k data digits but also by the previous N-1 data digits. An (n, k, m) convolutional code is a convolutional code that creates n outputs at a particular time from k inputs and m preceding inputs.
Q2. What is the difference between convolution codes and block codes ?
Ans. Convolutional codes differ from block codes in that the encoder output is created utilising part of the previous encoder inputs as well as a single input. In a nutshell, the encoder has memory.
Q3. Define minimum free distance of a convolutional code.
Ans. A convolutional code’s minimal free distance is defined as the shortest distance between any two encoded sequences and is given by the minimum-weight sequence of any length created by a non-zero input sequence.
Q4. What do you mean by state of a register ?
Ans. The state of a register is defined as the contents of the stages at a given point during encoding.
Q5. What do you mean by Viterbi algorithm for decoding of convolutional codes ?
Ans. A Viterbi algorithm is the algorithm that operates by computing a metric or discrepancy for every possible path in trellis.
Q6. What is the difficulty that may arise in Viterbi algorithm ?
Ans. A potential issue with using the Viterbi algorithm is that when the pathways entering a state are compared, their matrices are found to be identical.
Q7. Define the constraint length of a convolution code.
Ans. A convolution code’s constraint length is defined as the number of shifts through which a single message bit can impact the encoder output.
Q8. Define coding gain.
Ans. The coding gain is given as,
A = rdf/2
where, r = code rate, df = free distance
Q9. Give the comparison between code free and trellis diagram.
Ans.
| S. No. | Code tree | Trellis diagram |
| 1. | Code tree indicates flow of the coded signal along the nodes of the tree. | Trellis diagram transitions from current to next states. |
| 2. | Code tree is lengthy way of representing coding process. | Code trellis diagram is shorter or compact way of representing coding process. |
| 3. | Code tree is complex to implement in programming. | Trellis diagram is simpler to implement in programming. |



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Information Theory and Coding Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Information Theory and Coding Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One View) | Student Result |

1 thought on “Btech Aktu Information Theory and Coding KEC-075 Short Question, Notes, Quantum Pdf”