B.Tech AKTU Quantum Book will introduce you to the world of Industrial Engineering. To succeed in this profession, access crucial notes, repeated questions, and helpful insights. Unit-5 Operational Analysis
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Industrial Engineering: *Quantum *B.tech-Syllabus *Circulars *B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. What do you mean by linear programming problem (LPP) ? Describe the basic elements in a LPP.
Ans. A. Linear Programming Problem (LPP):
- 1. The optimisation (maximization or minimization) of an objective function, a function of variables, is the focus of linear programming. Constraints are a collection of linear equality conditions that may also include inequalities.
- 2. According to a predetermined standard for optimality, linear programming is a mathematical technique that includes allocating finite resources in the best possible way.
- 3. Using the resources at hand, linear programming is a method for choosing the best schedule of interconnected tasks.
- 4. Scheduling is referred to as programming. Choosing a certain course of action from a range of options is the process of programming, which is merely another word for planning.
- 5. The word linear indicates that all relationships involved in a particular problem are linear.
B. Basic Elements in LPP:
- a. Decision Variables and their Relationship: Candidates who are vying for a share of the available scarce resources are referred to as the decision variables.
- b. Well-defined Objective Function: A linear programming problem must have a clearly defined objective function to optimize. This objective function may be to maximize contribution by making use of resources that are already available or it may be to produce at the lowest cost possible by utilizing a finite number of productive factors.
- c. Presence of Constraints or Restrictions: When using few resources for a variety of competitive activities, there must be restrictions or limitations.
- d. Alternative Courses of Action: Other options must exist; for instance, it must be possible to choose from a variety of combinations.
- e. Non-Negative Restriction: As negative values of physical quantities are an impossibility, all decision variables must be assumed to have non-negative values.
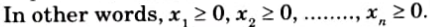
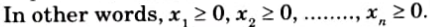
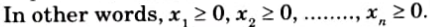
Q2. How will you solve a LPP using graphical method ?
Ans. Simple linear programming problems of two decision variable can be easily solved by using graphical method as follows:
- Step 1: Consider each inequality constraint as equation.
- Step 2: Plot each equation on the graph, as each one will geometrically represent a straight line.
- Step 3: Shade the feasible region. Every point on the line will satisfy the equation of the line. If the inequality constraint corresponding to the line is ≤, then the region below the line lying in the first quadrant is shaded. The points lying in common region will satisfy all the constraints simultaneously. The common region thus obtain is called a feasible region.
- Step 4: Choose the convenient value of Z (say = 0) and plot the objective function line.
- Step 5: Up to the outermost limits of the viable zone, draw the objective function line. This line will come to a stop the furthest from the origin and pass through at least one corner of the viable region in the maximization situation.
- Step 6: Read the coordinates of the extreme points selected in step 5, and find the maximum or minimum value of Z.
Q3. Explain the variations of the assignment problem.
Ans. Variations of the assignment problem are as follows:
a. The Maximal Assignment Problem:
- 1. Occasionally, the assignment problem involves maximization rather than minimization of an objective function. For instance, it can be necessary to place workers in occupations so that the predicted profit is maximized.
- 2. By first turning this into a minimization problem and then using the standard assignment algorithm process, this problem may be easily solved.
- 3. This conversion is relatively simple to complete by deducting all of the elements of the specified profit matrix from the highest element, or, alternatively, by putting a minus sign in front of each element of the profit matrix to turn it into a cost matrix.
b. Restrictions on Assignment:
- 1. There are instances when technical, legal, or other limitations prevent the assignment of a certain facility to a specific work.
- 2. You can get around this problem by giving the related cell an extremely high cost, which will automatically remove the activity from the best possible solution.
Q4. What is simulation ? Explain elements and structure of simulation system ?
Ans. A. Simulation:
- 1. Due to their complexity and probabilistic character, many situations in real life cannot be analytically modelled.
- 2. Without disrupting the system, it evaluates the impact of alternative policies.
- 3. Using a simplified system, simulation is a technique for conducting tests to examine the behaviour and gauge the effectiveness of genuine systems in real environments.
- 4. Simulation is the portrayal of reality using a model or other tool that will behave realistically under a specific set of circumstances.
- 5. The usage of a system model with designed properties of reality in order to produce the essential elements of actual operation is known as simulation.
B. Elements and Structure of Simulation System:
- a. State Variables: The type of the problem will determine which variables are needed to describe the physical system. State variables are the name given to these variables.
- b. Random Variables: The outcome of a theoretical chance experiment is related with the random variable, which is a real valued function defined over a sample space.
- c. Event: An event is an occurrence that results in a change in the state variables and a corresponding change in the system’s state.
- d. Static and Dynamic Simulation Model: A static simulation model examines a system’s profile at a specific period.
- e. Random Number: The likelihood of its recurrence is the same as that of every other number in the sequence of numbers.
Q5. Enumerate the special cases that may arise while solving a linear programming problem ?
Ans. a. Infeasible Solution:
1. It is considered to have an infeasible solution when there isn’t a value for the decision variables that meets all of the LPP constraints.
Example: Maximize Z = 4x1 + 2x2
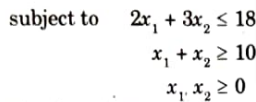
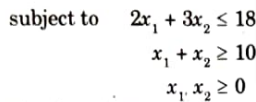
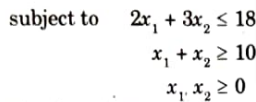
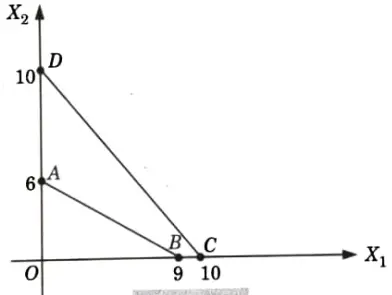
2. Solution of this expression:
i. Line AB represents
2x1 + 3x2 = 18
and line CD represents
x1 + x2 = 10
ii. In the Fig. there is no point which satisfies both the constraints in first quadrant. Hence, problem cannot be solved or given LP problem has no feasible solution.


b. Multiple Optimal Solution: The LPP is said to have numerous ideal solutions when more than one value of the decision variables results in the same optimal value of the objective function. These values of the decision variables are referred to as alternate optimal solutions.
c. Redundancy: If the feasible region of the issue is unaffected by removing a constraint from the specified LPP, the constraint is said to be redundant.
d. Unbounded Solution: Such an LPP solution is referred to as an unbounded solution when the value of the objective function can be increased or decreased indefinitely without any restrictions. There might or might not be an ideal answer in this case.
Q6. What is Monte-Carlo simulation ? Discuss in brief.
Ans.
- 1. John Von Neumann and Stanislaw Ulam, two mathematicians, created the Monte-Carlo method of simulation. The method offered a rough but largely practical answer to the issue.
- 2. The method uses random numbers to tackle probability-related issues when both actual investigation and the creation of mathematical models are impractical. It is a technique for simulating sampling methods.
- 3. The steps involved in carrying out Monte-Carlo simulation are:
- Step 1. Choose the problem’s objective function as the efficacy indicator. It has to be either maximized or minimized. For instance, it may be the amount of downtime a service facility experiences during a backlog, the quantity of shortages, or the entire cost of the inventory during an inventory control issue.
- Step 2. Determine the elements that significantly influence the efficacy measure. Examples include the quantity of service facilities involved in a queue issue or the demand, lead time, and safety stock involved in an inventory control issue.
- Step 3. Determine the cumulative probability distribution of each variable selected in step 2. Plot these distributions with values of the variables along x-axis and cumulative probability values along the y-axis.
- Step 4. Get a set of random numbers.
- Step 5. As a decimal value of the cumulative probability distribution, treat each random integer as such. Along the y-axis, start the cumulative distribution plot. This point should be horizontally projected until it touches the distribution curve. Project the intersection’s point downward onto the x-axis after that.
- Step 6. Record the value (or values) generated in step 5. Substitute in the formula chosen for measure of effectiveness and find its simulated value.
- Step 7. Repeat step 5 and 6 until sample is large enough to the satisfaction of the decision maker.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Industrial Engineering Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Industrial Engineering Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
