In This Blog we are discussing for Unit03 Flow Through Pipes, Boundary Layer Thickness in Fluid Mechanics & Fluid Machines AKTU Important Questions. Hope you will enjoy that session, also help in upcoming exams.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Fluid Mechanics & Fluid Machines : *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
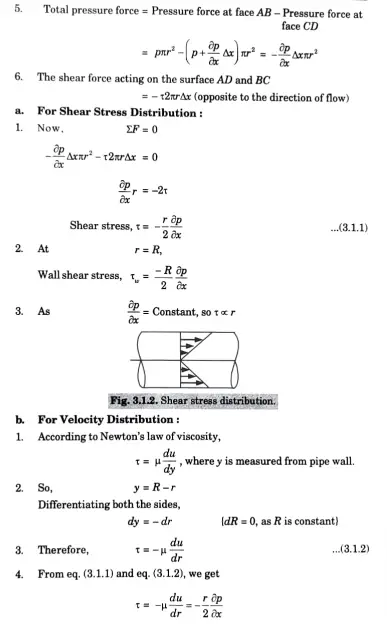
Q1.What are the characteristics of a laminar flow ? Derive the expression for the velocity distribution for viscous flow through a circular pipe. Also sketch the distribution of velocity and shear stress across a section of pipe.
Answer
A Characteristics of Laminar Flow:
- 1. Laminar flow obeys Newton’s law of viscosity.
- 2. The laminar flow is rotational.
- 3.No slip will occur at the boundary of laminar flow
- 4.There will be no mixing of layers occurring in laminar flow.
- 5. For laminar flow, Reynold’s number < 2000.
B. Derivation for Velocity and Shear Stress Distribution:
Let us consider a horizontal pipe having diameter d and radius R.
Direction of fluid is shown in Fig. 3.1.1
Take a fluid element in between the radius r and r + dr and length of the
fluid element be Δx
If p is the pressure on the face AB, then pressure on face CD will be
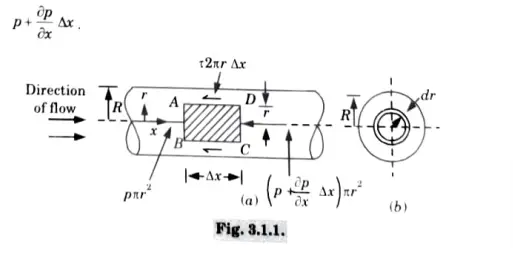




Q2.A compound piping system consists of 1800 m of 0.50 m,1200 m of 0.40 m and 600 m of 0.30 m new cast iron pipes connected in series. Convert the system to (a) an equivalent length of 0.40 m pipe, and (b) equivalent size pipe of 3600 m long



a. Displacement Thickness
- It can be defined as the distance, measured perpendicular to the boundary by which the main/free stream is displaced on account of formation of boundary layer. It is denoted by δ*
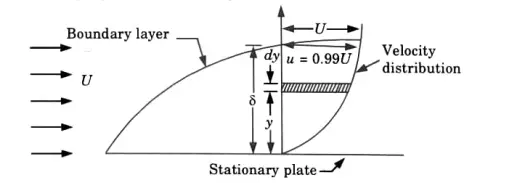


- Let fluid of density p flow past a stationary plate with velocity U as shown in Fig.
- Consider an elementary strip of thickness dy at a distance y from the plate
- Mass flow per second through the elementary strip = pudy
- Mass flow per second through elementary strip, if the plate was not there = pUdy
- Reduction of mass flow rate through elementary strip p(U- u) dy
- Total reduction of mass flow rate due to introduction of plate
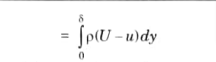
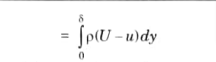
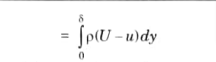
- Let the plate is displaced by a distance δ* and velocity of flow for the distance δ* is equal to the main/free stream velocity. Then, loss of mass of fluid/sec flowing through the distance δ*
- =pUδ*
- On equating eq. (3.22.1) and eq. (3.22.2), we get
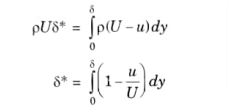
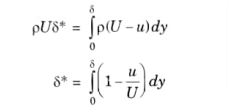
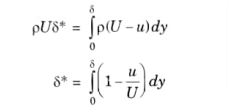
b. Momentum Thickness:
- It is defined as the distance, measured perpendicular to the boundary Of the solid body, by which the boundary should be displaced to compensate for the reduction in momentum of the flowing fluid on account of boundary layer formation. It is denoted by θ.
- Mass of flow per second through elementary strip = pudy
- Momentum/sec of this fluid inside the boundary layer (pudy * u = pu-dy)
- Momentum/sec of the same mass of fluid before entering the boundary layer = puUdy
- Loss of momentum/sec= puUdy-pu2dy = pu(U – u) dy
- Total loss of momentum/sec
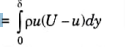
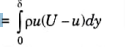
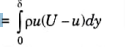
Let θ be the distance by which plate is displaced when fluid is flowing with a constant velocity U. Then, loss of momentum/sec of fluid flowing through distance θ with a velocity U
=pθU2
On equating eq. (3.22.3) and eq. (3.22.4), we get
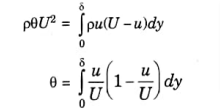
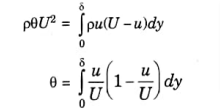
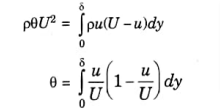
c. Energy Thickness:
It is defined as the distance, measured perpendicular to the boundary of the solid body, by which the boundary should be displaced to compensate for the reduction in kinetic energy of the flowing fluid on account of boundary layer formation. It is denoted by δe or δ**
Mass of flow per second through elementary strip = pudy
KE of this fluid inside the boundary layer
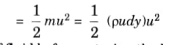
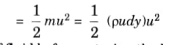
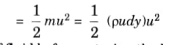
KE of same mass of fluid before entering the boundary layer
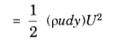
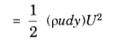
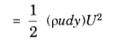
Loss of KE through elementary strip
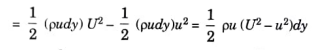
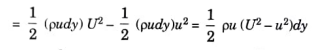
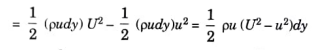



Q4. Oil with density 900 kg/m3 and kinematic viscosity 10-5m2/sec is flowing over a plate of 3 m long and 2 m wide with a velocity of 3 m/sec parallel to 3 m side. Find the boundary layer thickness at the point of transition and at the end of the plate.



Q5 What is boundary layer separation ? Explain with neat sketches, the necessary conditions for boundary layer separation. What are common methods to control boundary layer separation ?
Answer
A Boundary Layer Separation :
- When a solid body is kept or immersed in a flowing fluid, boundary layer is formed adjacent to the solid body
- Within this thin layer of fluid, the velocity varies from zero to free stream velocity in the direction normal to the solid body.
- Along the length of the solid body, the thickness of the boundary layer increases
- The fluid layer adjacent to the solid surface has to do work against surface friction at the expense of its kinetic energy
- This loss of the kinetic energy is recovered from the immediate fluid layer in contact with the layer adjacent to solid surface through momentum exchange process. Thus the velocity of layer goes on decreasing.
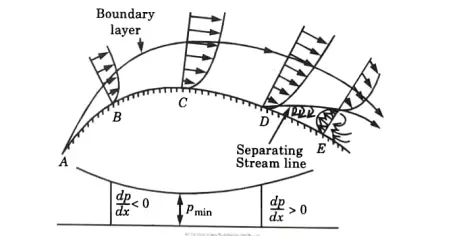


- Along the length of the solid body, ata certain point a stage may come when the boundary layer may not be able to keep sticking to the solid body if it cannot provide kinetic energy to overcome the resistance offered by the solid body. Thus, in other words, the boundary layer will get separated from the surface. This phenomenon is called the boundary layer separation
- The point on the body at which the boundary layer is on the verge of separation from the surface is called point of separation.
B. Necessary Conditions for Boundary Layer Separation: For boundary layer separation, pressure gradient should be positive in the



C. Methods to Control Boundary Layer Separation
i. Streamlined Body Shape:
- Using streamlined body shape, the transition point of boundary layer (from laminar to turbulent) can be moved downstream which results in the reduction of the skin friction drag. Hence, separation of layers may be eliminated
ii. Acceleration of Fluid in the Boundary Layer:
- In this method, we supply additional energy to the particles of fluid which are being retarded in the boundary layer.
- Energy can be transferred by:
- Injecting the fluid into the region of boundary layer with the
help of some device. - Diverting a portion of fluid from high pressure region to the
retarded region of boundary layer through a slot provided in
the body.
- Injecting the fluid into the region of boundary layer with the
iii. By sucking the retarded flow.
iv. By providing slots near the leading edge.
v. Energising the flow by introducing optimum amount of swirl in the incoming flow.
vi. Remove the retarded or slow moving fluid particles in the boundary
layer by suction through a porous surface.
Q6. Explain the Magnus effect with an example.
Answer
A Magnus Effect
1. A lift force is generated on a cylinder when it is spun in a uniform flow.
2. Magnus effect is the name given to the phenomenon of the lift force generated by a revolving cylinder in a uniform flow.
B. Example:
1. The propulsion of ships has successfully used this effect.
2. The Magnus effect can be advantageously applied in sports like cricket, golf, and table tennis.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Fluid Mechanics & Fluid Machines Quantum, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Fluid Mechanics & Fluid Machines Quantum PDF: | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |

6 thoughts on “Unit03 Flow Through Pipes, Boundary Layer Thickness | Fluid Mechanics & Fluid Machines AKTU”