The B.Tech AKTU Quantum Book will teach you the technique of Digital Signal Processing. Gain access to critical notes, frequently asked questions, and insightful information in this field. Unit-3 FIR Filter Design
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Digital Signal Processing: *Quantum *B.tech-Syllabus *Circulars *B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. What is reason that FlR Filters are always stable ? Also write the properties of FIR filter.
Ans. A. Reason:
- 1. The impulse response of FlR filter is h(n) = an u(n)
- 2. It has all non-zero for n ≥ 0 ie., it has infinite number of non-zero terms. The difference equation for FIR filter is:
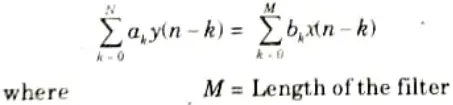
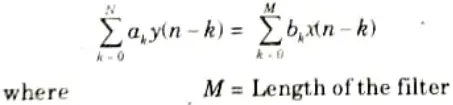
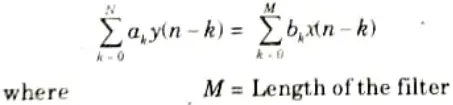
- 3 The filter response is given as,
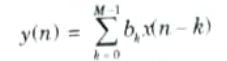
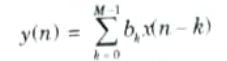
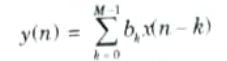
Eq. only has zeros in right half and poles. Thus FIR filters are always stable.
B. Properties of FIR filters:
- i. They have linear phase.
- ii. They are always stable.
- iii. Their design methods are generally linear.
- iv. They can be realized efficiently in hardware.
- v. The filter start-up transients have finite duration.
Q2. Explain the Kaiser window.
Ans. 1. All the window functions have variable width of main lobe. It is inversely proportional to the length of the filter.
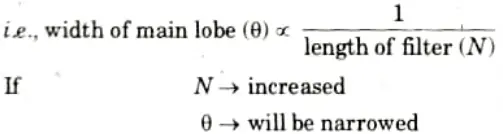
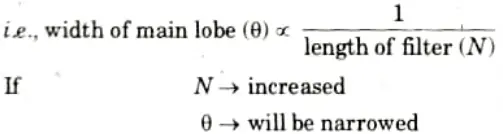
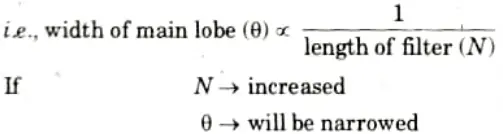
It means at higher value of N the transition band is reduced considerably.
- 2. The attenuation in the sidelobe should be independent of window length and type. To obtain the appropriate stop band attenuation, the proper window function must be chosen.
- 3. A desirable window function in the time domain should have a finite lifetime and its fourier transform should have maximum energy in the main lobe or a given peak sidelobe amplitude.
- 4. Kaiser has developed a simple approximation to these functions in terms of 0th order modified bessel functions of the first kind.
- 5. Here the sidelobe energy level is controlled with respect to the main lobe peak by just varying a parameter ‘𝞪’. By adjusting the length of the filter, the width of the main lobe can be varied.
- 6. The Kaiser window is defined as,
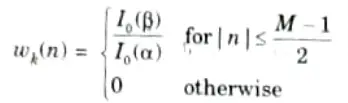
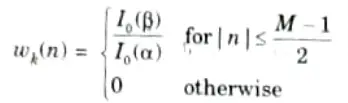
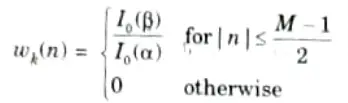
where 𝞪 is an independent variable determined by Kaiser.
- 7. The parameter β is expressed by
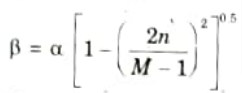
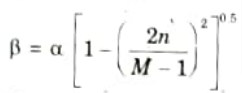
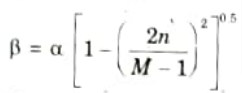
- 8. The modified bessel function of the first kind is given as,
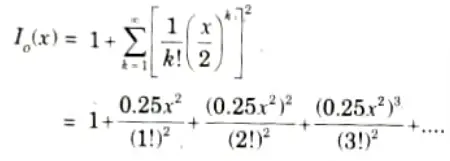
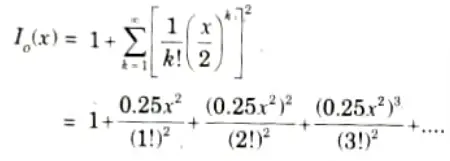
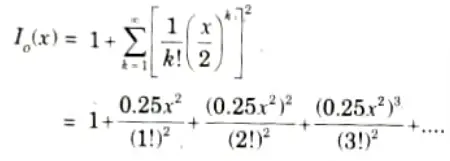
Q3. Write a short note on the following :
i. Bartlett window.
ii. Blackman window.
Ans. i. Bartlett window:
1. It is also called as triangular window. It is expressed mathematically as:
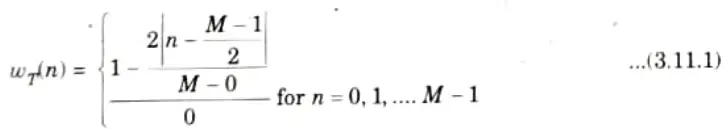
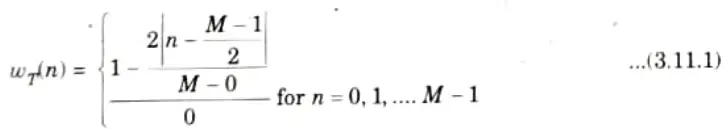
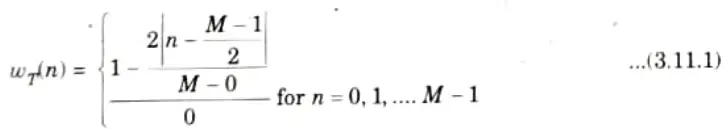
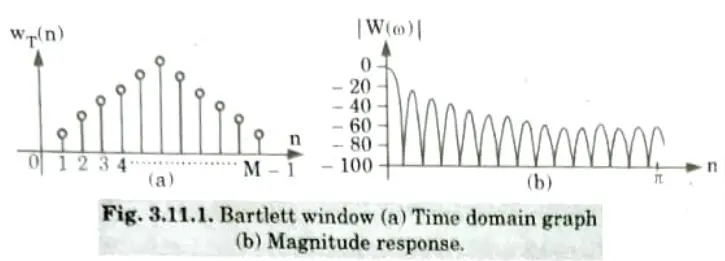
2. Fig. 3.11.1(a), shows the sketch of this window. Fig. 3.11.1(b), shows the magnitude response of this window.


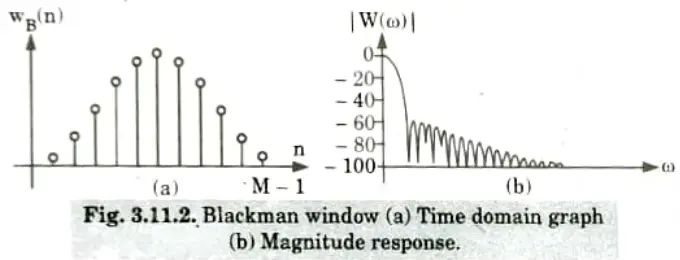
ii. Blackman window:
1. It is expressed mathematically as:
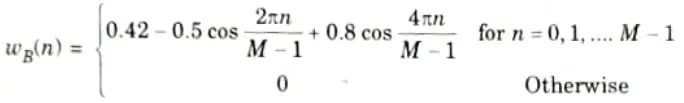
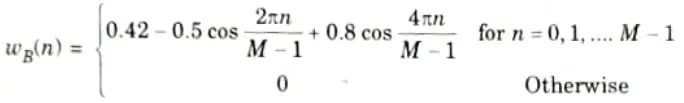
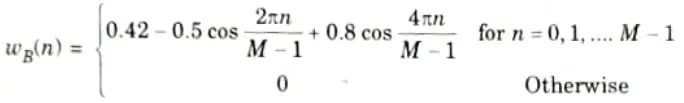
2. Fig. 3.11.2(a), shows the graph of Blackman window. Fig. 3.11.20(b) shows its magnitude response. In this, the width of the main lobe is increased. However, it has very small sidelobes.


Q4. A filter is to be designed with the following desired frequency response:
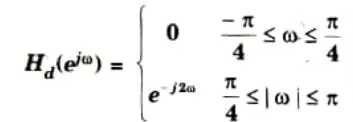


Ans.
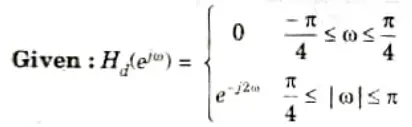
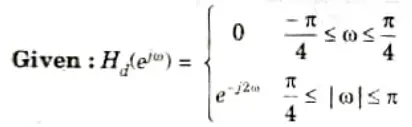
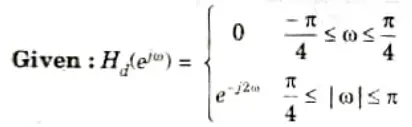
To Design: Filter.
1. Impulse response of the filter is given as






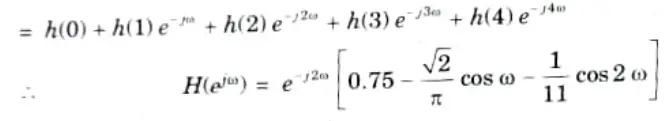
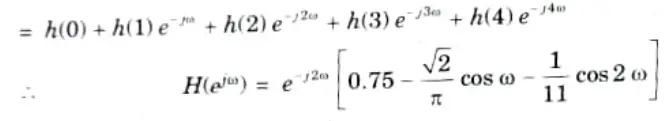
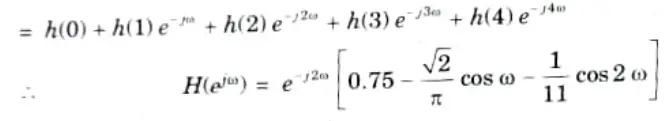
Q5. Discuss the Finite Word length effects in digital filters.
Ans.
- 1. Multiplication and addition are the essential operations in digital filters. When performing these operations in a digital system, the input data, as well as the product and sum (output data), must be represented in finite word lengths, which are determined by the size (length) of the resistor used to store the data.
- 2. In digital computation, input and output data (sum and product) are quantized by rounding or truncation to fit within a finite word size. This results in inaccuracy (in noise) or oscillations (limit cycle) in the output.
- 3. These effects due to finite precision representative of number in digital system are called as finite word length effects.
- 4. List some of the finite word length effects in digital filters:
- i. Errors due to quantization of the input data.
- ii. Errors due to quantization of the filter coefficients.
- iii. Errors due to rounding the product in multiplications.
- iv. Limit cycle due to product quantization and overflow in addition.
Q6. Write a note on round-off noise in Digital filter.
Ans.
- 1. A multiplier’s output has more bits than its inputs. The output must be (re)quantized before it can be stored. At that point, a mistake known as quantization noise or round off noise is introduced.
- 2. The quantization noise at each multiplier output is frequently believed to be white (independent from sample to sample).
- 3. It is also expected that the noise variances are additive between multipliers.
- 4. The assumption of whiteness is a poor model for narrowband signals, but it is suitable for big amplitude wideband signals. The assumption of independence might be a poor model as well.
- 5. As a result, the quantization noise from a FIR filter’s multipliers directly contributes white noise to the output signal.
- 6. With lIR filters, the white quantization noise from the feedback multipliers filter is fed to the filter’s input, resulting in a coloured noise spectrum at the filter output.
- 7. The spectrum is proportional to the square of the frequency response magnitude of the filter.
- 8. Data wordlengths, filter response, filter structure, and (to a lesser extent) section ordering in cascade structures all influence round-off noise level.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Digital Signal Processing Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Digital Signal Processing Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One View) | Student Result |
