Master the skill of Digital Signal Processing with the B.Tech AKTU Quantum Book. Gain access to important notes, frequently asked questions, and helpful insights in this industry. Unit-2 IIR Filter Design
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Digital Signal Processing: *Quantum *B.tech-Syllabus *Circulars *B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
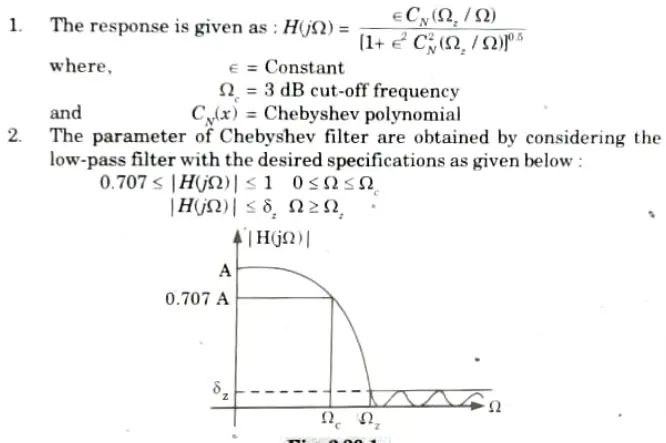
Q1. What is filter ? Explain its types.
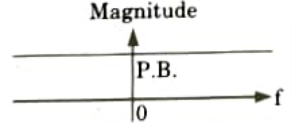
Ans. A. Filter: A filter is one that rejects undesired frequencies from an input signal while allowing the desired frequencies to pass through. The range of signal frequencies that pass through the filter is known as the passband (P.B.) while the range of frequencies that are blocked is known as the stopband (S.B.).
B. Types:
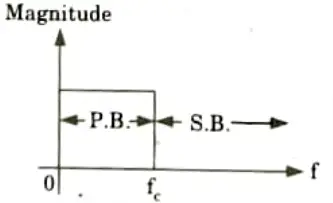
i. Low-pass filter: It shifts the frequency from zero to a predetermined frequency known as the cut-off frequency. After this frequency, no signal will be able to travel through it.


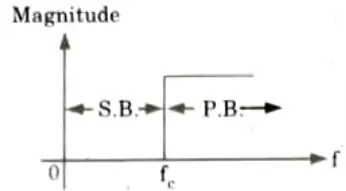
ii. High-pass filter: It raises the frequency above a certain threshold, known as the cut-off frequency. If the frequency of the input signal is less than the frequency of the cut-off. This signal is not permitted to flow through it.


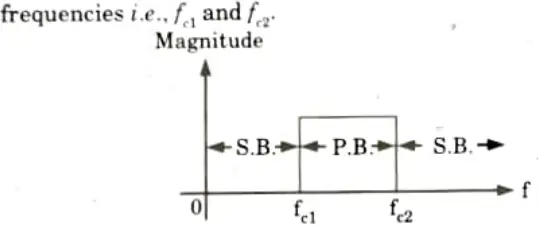
iii. Band-pass filter: It allows the frequencies between two designated


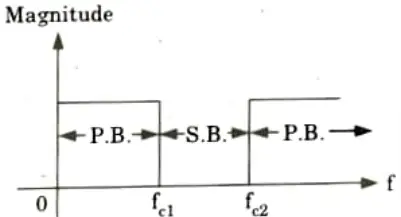
iv. Band-reject filter: It attenuates all frequencies between two designated cut-off frequencies. At the same time it passes all other frequencies.


v. All-pass filter: It passes all the frequencies. By using this filter the phase of input signal can be modified.


Q2. The system function of analog filter is given by
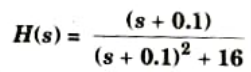
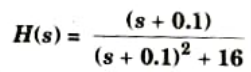
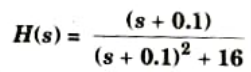
Obtain the system function of digital filter by using impulse invariant technique. Assume T = 1 sec.
Ans.
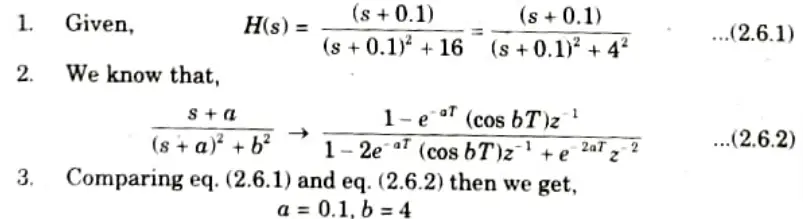
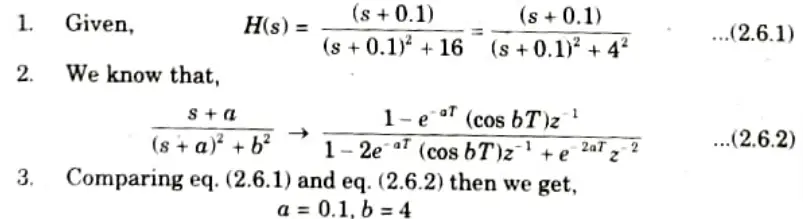
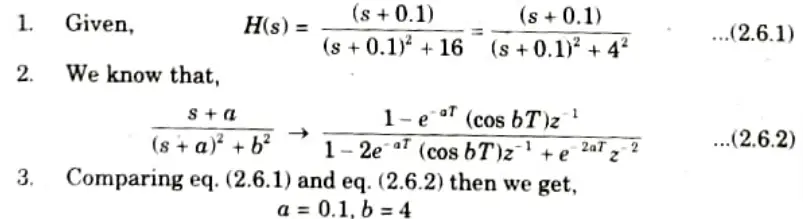
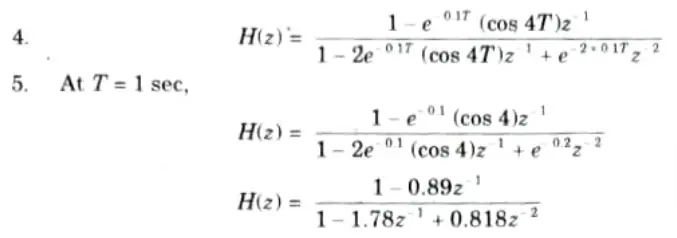
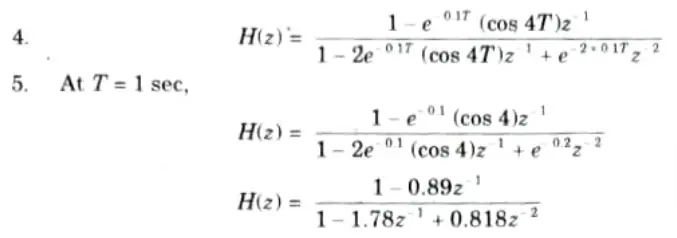
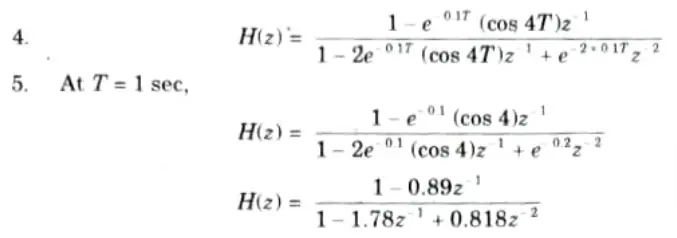
Q3. Discuss the bilinear transformation method of converting analog IIR filter into digital IIR filter.
Ans.
- 1. Bilinear transformation is a one to one mapping from the s-domain to the z-domain.
- 2. Bilinear transformation is a conformal mapping that transforms the jΩ-axis into the unit circle in the z-plane only once. Thus the aliasing effect is avoided.
- 3. As all the poles in the left half of the s-plane are mapped onto points inside the unit circle of the z-domain, the transformation of a stable analogue filter results in a stable digital filter.
- 4. It is obtained by using the trapezoidal formula of numerical integration.



- 6. On comparison real and imaginary part we get,



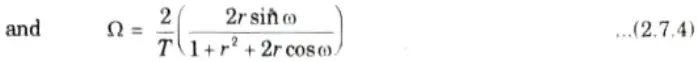
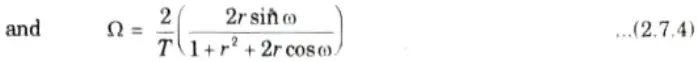
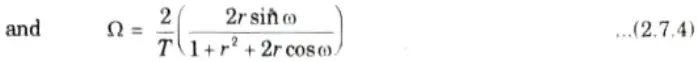
- 7. On the basis of value of r three cases can be discussed as below :
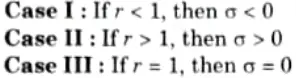
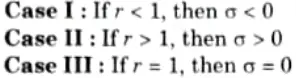
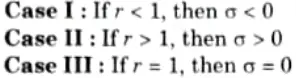
From all three cases it is clear that the left half of the s-plane is mapped on to the points inside the unit circle in the z-plane.
Q4. Discuss Chebyshev type-II filter.
Ans.


Q5. Explain frequency transformation with LPF to HPF conversion formula.
Ans. 1. The frequency transformation formulae used to convert a prototype lowpass filter into a low pass (with a different cut-off frequency), high pass, band pass or band stop are given below.
2. To convert low-pass with cut-off frequency Ωc to high-pass with cut-off frequency
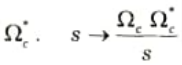
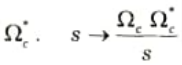
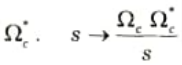
The system function of the high-pass filter is then,
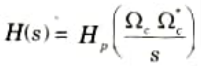
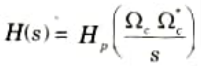
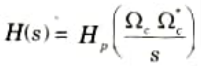
3 In the digital domain the frequency transformation is done replacing the variable z-1 by a function of z-1, i.e. f(z-1). This mapping must take into account the stability criterion.
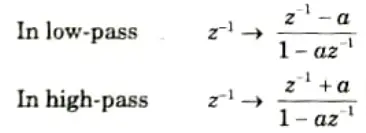
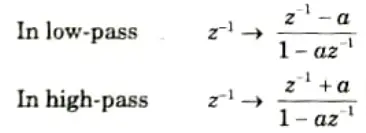
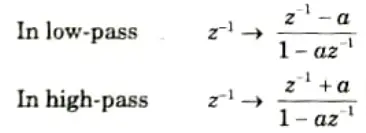
Q6. Determine H(z) using the impulse invariant technique for the analog system function.
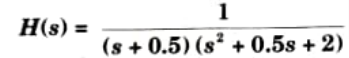
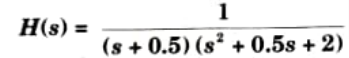
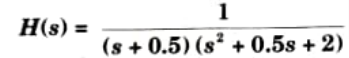
Ans. 1. Using partial fractions, H(s) can be written as,
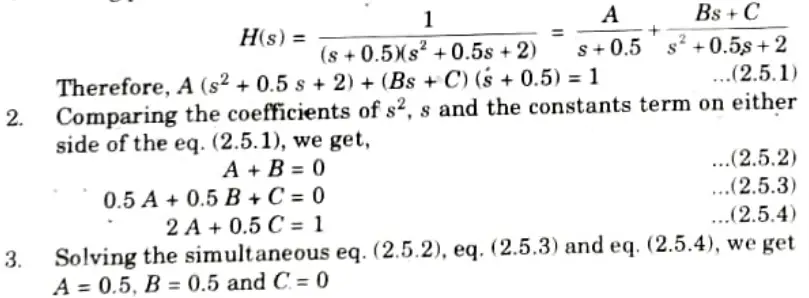
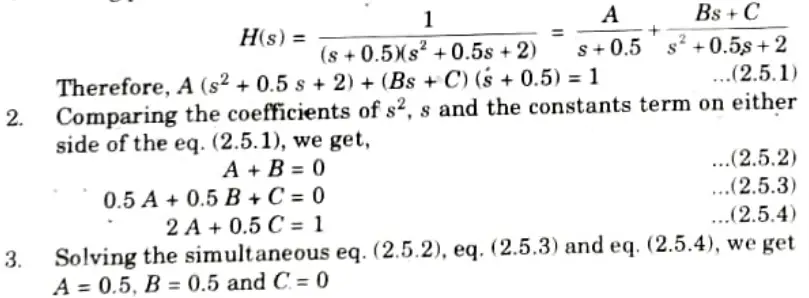
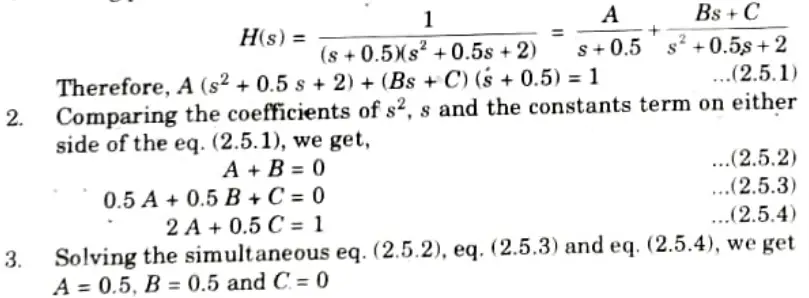
4. The system response can be written as,









Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Digital Signal Processing Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Digital Signal Processing Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One View) | Student Result |
