Aktu’s Quantum Notes are used to master Control Systems. Access critical insights and frequently asked questions to help you succeed in your B.Tech studies. Your route to success begins right here! Unit-3 Stability and Algebraic Criteria
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Control System: *Quantum *B.tech-Syllabus *Circulars *B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. Define stability. Also write the necessary conditions for stability ?
Ans. A. Stability:
- 1. A system is considered stable if its response, or transfer function, decreases as time increases towards infinity.
- 2. In other words, if every bounded input results in a bounded output, the system is stable.
B. Types of stability:
- 1. Absolute stability: A system is said to be perfectly stable if the output is constant for all variations in its parameters. It provides information on how stable or unstable the system is.
- 2. Relative stability: On the basis of the settling time, the system is deemed to be relatively more stable or unstable. If the system’s settling time is shorter than that of the competing system, the system is deemed to be substantially more stable. The degree of stability or how close to instability it is is indicated by relative stability.
C. Necessary conditions for stability:
- 1. All the coefficients of characteristics equation must have same sign.
- 2. There should be no missing term.
- 3. All poles of transfer function should be in left half of s-plane.
- 4. The degree of denominator polynomial of transfer function is greater or equal to that of numerator polynomial.
Q2. Explain stability on basis of location of poles and zeros.
Ans.
- 1. The linear system is stable if the rightmost pole(s) is/are on the left hand half plane (LHHP) on the s-plane
- 2. The linear system is marginally stable if the rightmost pole(s) is/are simple order (first-order) on the jω axis, including the origin on the s-plane.
- 3. The linear system is unstable if the rightmost pole(s) is/are on the right-hand half plane (RHHP) of the s-plane or if the rightmost pole(s) is/are multiple-order on the jω axis on the s-plane.
- 4. Zeros do not affect system Stability.
Q3. What is root locus ? Also give the salient features of root locus.
Ans. A. Root Locus:
- 1. Root locus is the plot of loci of the root of the complementary equation when one or more parameter of open-loop transfer function is varied; mostly the only one variable available is the gainK. The negative K has no significance. Hence vary K from 0 to ∞, the plot obtained is called root locus.
- 2. It gives the complete dynamic response of system. It provides the measure of sensitivity of roots of variation in the system.
B. Features:
- 1. The root locus starts (K = 0) from the open loop poles and terminates (K=∞) on either finite open loop zeros or infinity.
- 2. The number of distinct branches at the root locus is equal to the greater of the number of open loop poles or open loop zeros.
- 3. If the total number of open loop poles and zeros to the section’s right is odd, the section of the root locus is on the real axis.
- 4. With regard to the real axis, the root locus is symmetrical.
- 5. The root locus between two open loop poles occasionally separates at certain places.
- 6. Asymptotic lines that meet at a point on the real axis can be used to approximate the root locus for greater values of K.
- 7. If the root locus intersects the imaginary axis then the point of intersection is conjugate.
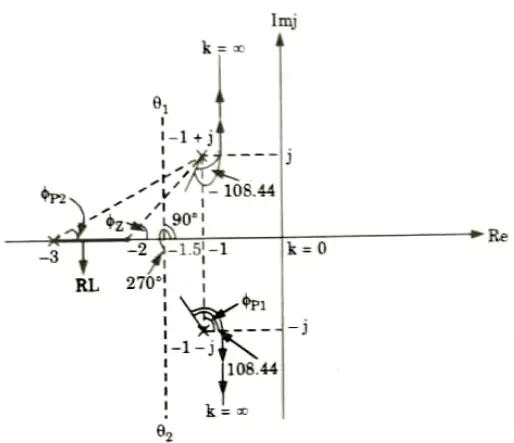
Q4. A unity feedback system has an open loop transfer function.
Draw the root locus for the system.
G(s) H(s) =k (s + 2)/(s +3) (s2+2s +2)
Ans.
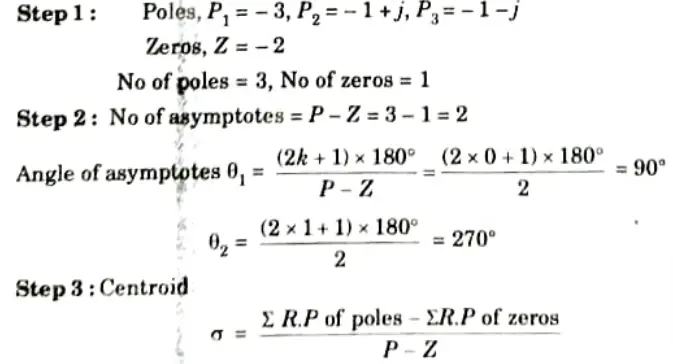
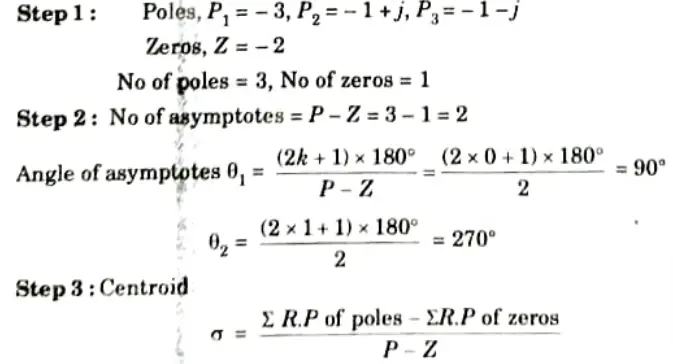
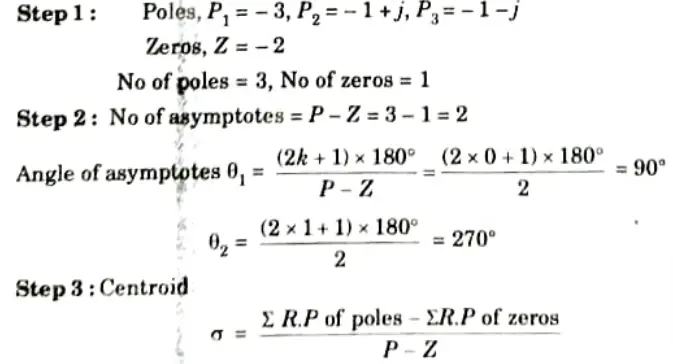
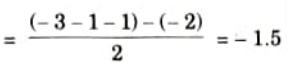
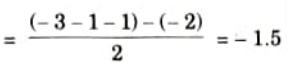
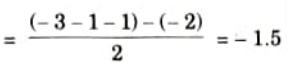
Step 4: Breakaway point: Characteristics equation,
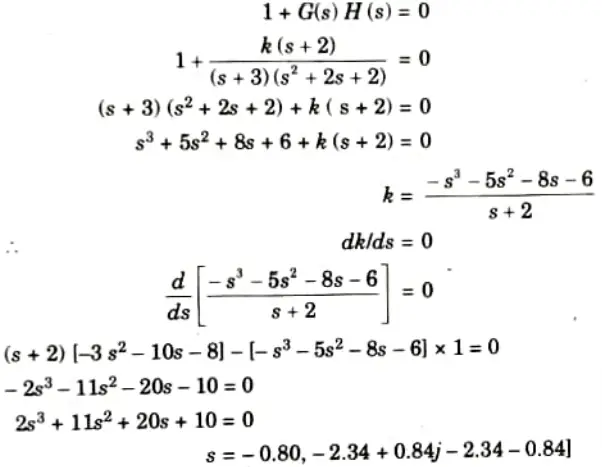
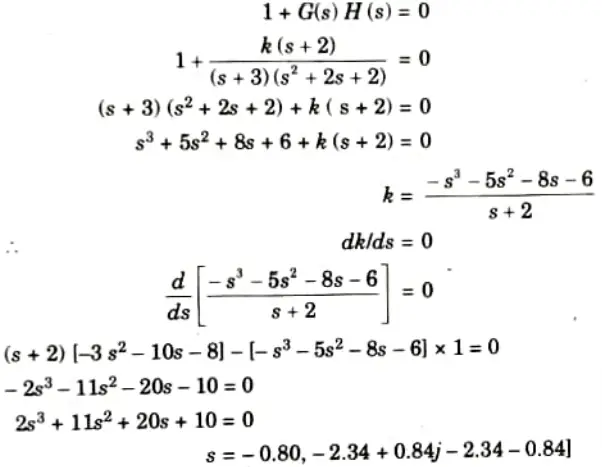
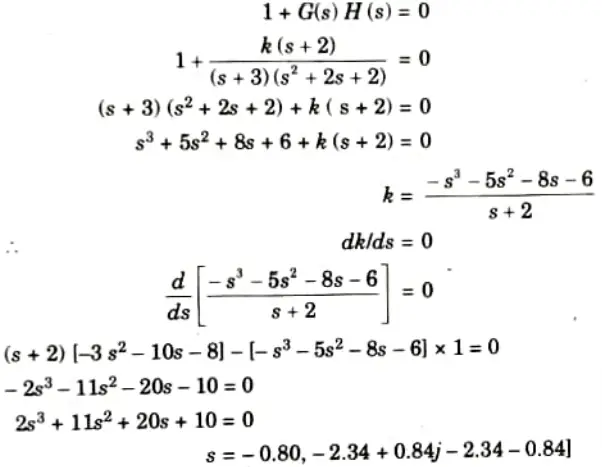
That breakaway point is not valid
Step 5: Intersection point: Characteristics equation,



Auxiliary equation 5s2 + 6 + 2k = 0


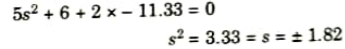
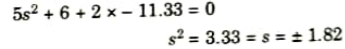
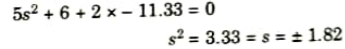
That intersection point is not valid.
Step-6: Angle of departure:
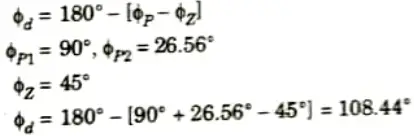
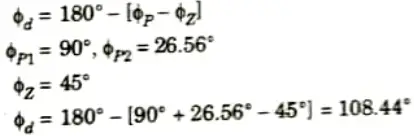
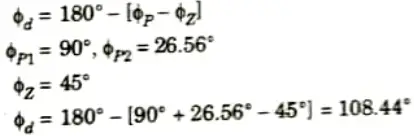
Q5. Explain the effect of addition of pole and zero on root locus and time domain specifications.
Ans. A. Effects of addition of poles:
- 1. Root locus shifts towards imaginary axis.
- 2. System stability relatively decreases.
- 3. System becomes more oscillatory in nature.
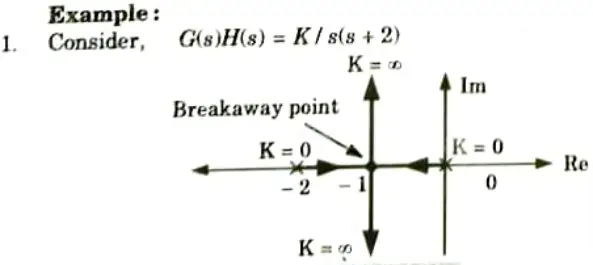


Corresponding root locus is shown in the Fig.
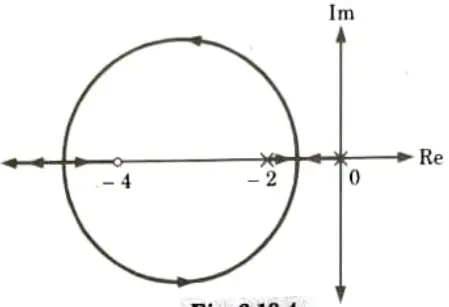
2. Now if pole at s = -4 added to G(s) H(s) root locus becomes as shown in the Fig.
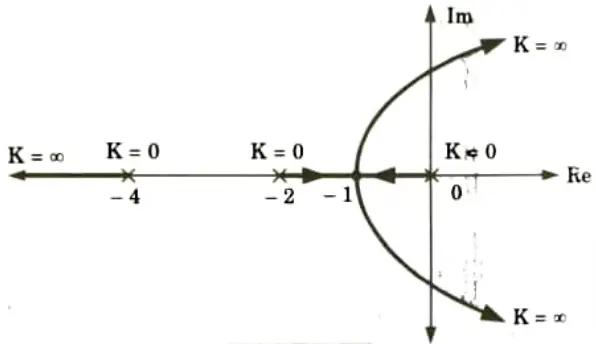


B. Effects of addition of zeros:
- 1 Root locus shifts to left, away from imaginary axis.
- 2. Relative stability of the system increases.
- 3. System becomes less oscillatory.
Example:
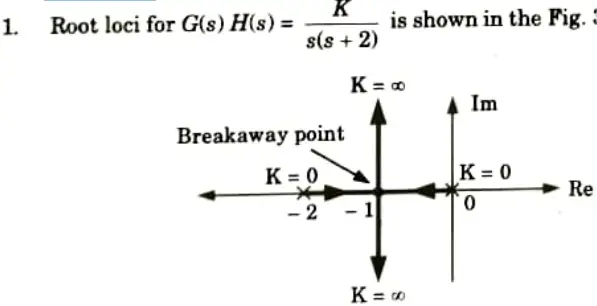


2. Now if zero at s = -4 added to G(s) H(s) root locus becomes as shown in Fig.
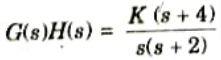
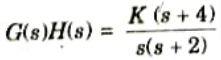
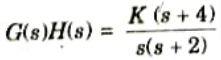
3. It can be seen that root locus shift towards left. So as roots move towards left half of s-plane, hence relative stability increases.


Q6. What are the limitations and applications of Routh-Hurwitz criterion ?
Ans. A. The Routh-Hurwitz stability criterion is a mathematical test that is a necessary and sufficient condition for the stability of system.
B. Routh’s criterion:
- 1. The necessary and sufficient condition for the system to be stable is that all the terms in the first column of Routh s array (i.e., a0,a1,b1,c1,d1…………….an) must have same sign.
- 2. There should not be any sign change in the first column of Routh’s array.
- 3. If there is any sign change then
- i. System is unstable.
- ii. Number of sign changes is equal to the number of poles lying in the right half of the s-plane.
C. Method of forming a Routh array:
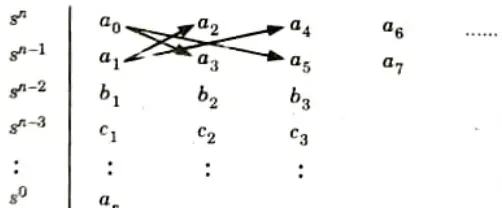


1. Coefficients for first two rows are written directly from characteristics equation,
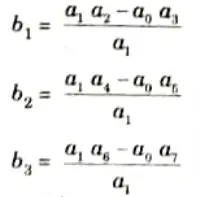
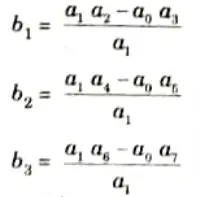
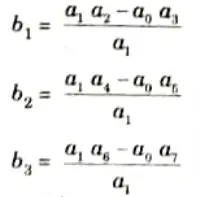
2. From 2nd and 3rd row, 4th row can be obtained as
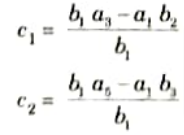
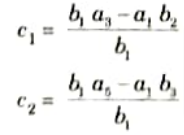
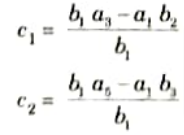
3. This process is to be continued till the coefficient for s0 is obtained which will be an From this array stability of a system can be predicated.
D. Special cases :
- 1. When the 1st term in a row is zero, but all other terms are non-zero then substitute a small positive number ε for zero & proceed to evaluate the rest of the elements. When the 1st column term is zero, it means that there is an imaginary root.
- 2. All zero row: In this scenario, create an auxiliary equation from the previous row, differentiate it, and then replace every zero row with the coefficient from the auxiliary equation’s differentiating operation. When the roots are in pairs, this scenario happens. Little stability is claimed for the system.
E. Application: Routh’s criterion can be used to identify the range of specific system parameters in order to assure stability. It is typically used to determine the open loop gain K range for closed loop stability.
F. Limitations:
- 1. It is only valid if the properties equation is algebraic.
- 2. This criterion cannot be used if any of the coefficients in the characteristics equation are complex or contain a power of e.
- 3. It indicates the number of roots in the RHS of the s-plane, but the values of the roots are not provided. It also can’t tell the difference between actual and complicated roots.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Control System Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Control System Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
