This year’s Thermodynamics exam paper at AKTU Btech (Mechanical Engineering) included questions on the first and second laws of thermodynamics, the Carnot cycle, entropy, compressors, and heat transmission. The paper was designed to assess students’ comprehension of fundamental ideas as well as their ability to use them to solve real issues.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Thermodynamics: *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Short Question in Thermodynamic Question Paper AKTU
a. Differentiate microscopic and macroscopic point of view.
Ans.
| S. No. | Macroscopic Approach | Microscopic Approach |
| 1. | It is used in classical thermodynamics. | It is used in statistical thermodynamics. |
| 2. | The term “system” refers to a continuum. voids or cavities, but a constant distribution of stuff. | It is believed that the system is made up of several molecules that are randomly moving. |
| 3. | Properties of system are their average values. Changes can be sensed by human. e.g., pressure, temperature etc. | Properties are defined for each molecule individually. (Properties like velocity, momentum, kinetic energy which describe a molecule) changes in it cannot be sensed by human. |
| 4. | Few properties are required to describe the system. | Large number of variables is required to describe the system. |
b. Define the quasi static process.
Ans. This process is a series of equilibrium states, and its distinguishing quality is infinite slowness. A reversible process is another name for this procedure.
c. Define the second law of efficiency and why PMM-II is not possible.
Ans. Second Law Efficiency: The ratio between the required minimum quantity of accessible energy (also known as exergy) and the actual amount of exergy used to complete a task is known as second law efficiency.



Reason for the impossibility of PMM-Il: PMM-II is not possible because it violates the Kelvin-Planck statement of second Law of thermodynamic.
d. Distinguish between high grade energy and low-grade energy.
Ans.
| S. No. | High Grade Energy | Low Grade Energy |
| 1. | It is possible to completely transform high-grade energy into low-grade energy. | It is not possible to completely transform low-grade energy into high-grade energy. |
| 2. | Work is high grade energy. | Heat is low grade energy. |
e. Explain the Joule-Thompson coefficient and inversion curve.
Ans. Joule-Thomson Coefficient: The temperature and pressure behaviour of fluids during a throttling process is described by the Joule-Thomson coefficient (µ).



Inversion Curve:
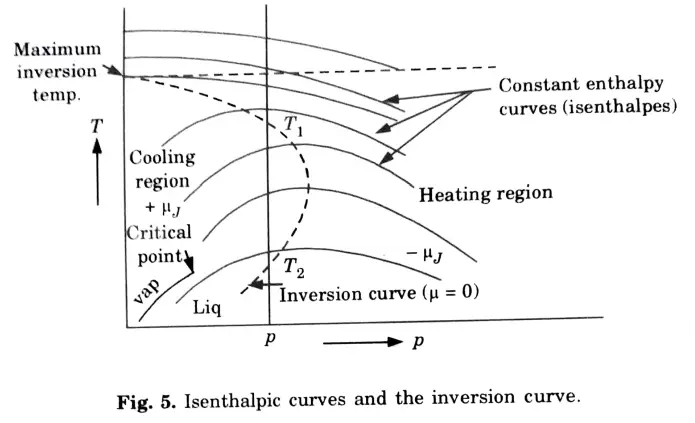


f. Discuss the triple point and critical point.
Ans. Triple Point: The term “triple point” refers to the temperature and pressure conditions at which a substance can coexist in equilibrium in all three of its states (solid, liquid, and vapour).
Critical Point: The critical point is where there is no longer a difference between the entropies of water and dry steam.
g. Define the refrigeration effect and how it can be improved?
Ans. Refrigeration Effect: The refrigeration effect is the quantity of heat removed from the system.
Ways of Improving Refrigeration Effect: Utilizing sub-cooling and super heating will enhance the refrigeration effect.
h. Explain the dryness fraction and how it can be improved?
Ans. Dryness Fraction:
1. The quality of the mixture depends on the proportional proportions of each component present in the wet steam, which is a mixture of saturated water and steam.
2. Dryness fraction of steam is defined as the ratio of mass of dry saturated steam to the total mass of mixture (i.e., ms+ mw)
3. It is generally denoted by x.
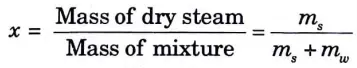
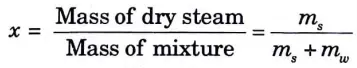
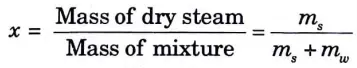
Method of improving Dryness Fraction: By superheating the vapour refrigerant before it enters the compressor, the dryness fraction can be increased.
i. How the COP of the vapor compression cycle can be improved?
Ans. Reduced compressor effort and increased refrigeration impact can boost the COP of the vapour compression cycle.
j. Differentiate between available and unavailable energy.
Ans.
| S. No. | Available Energy | Unavailable Energy |
| 1. | The available energy, or exergy, of a cyclic heat engine is the greatest work output produced from a given heat input. | The unavailable energy, or anergy, is the absolute minimum amount of energy that must be rejected to the sink in accordance with the second law. |
Section B : Important Question in Thermodynamics with solution
a. A nozzle is a device for increasing the velocity of a steadily flowing stream. At the inlet to a certain nozzle, the enthalpy of the fluid passing is 3000 kJ/kg and the velocity is 60 mis. At the discharge end, the enthalpy is 2762 kJ/kg. The nozzle is horizontal and there is negligible heat loss from it.
i. Find the velocity at exits from the nozzle.
ii. If the inlet area is 0.1 m2 and the specific volume at inlet is 0.187 m3/kg, find the mass flow rate.
Ans.



To Find: i. Rate of heat rejected.
ii. Area of the inlet pipe.



Hence, the rate at which heat is rejected to the turbine = 828 kJ/s
b. A heat pump working on the Carnot cycle takes in heat from a reservoir at 5 ℃ and delivers heat to a reservoir at 60 ℃. The heat pump is driven by a reversible heat engine which takes in heat from a reservoir at 840 ℃ and rejects heat to a reservoir at 60 ℃. The reversible heat engine also drives a machine that absorbs 30 kW. If the heat pump extracts 17 kJ/s from the 5 ℃ reservoir, determine.
i. The rate of heat supply from the 840 ℃ source
ii. The rate of heat rejection to the 60 ℃ sink.
Ans. Given : T1 = 5 ℃ = 5 + 273 = 278 K, T3 = 60 °C = 60 + 273 = 333 K, T2 = 840 °C = 840 + 273 = 1113 K, Q4 = 17 kJ/s
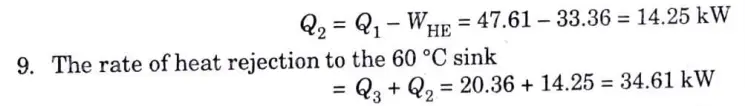
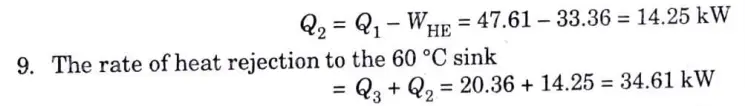
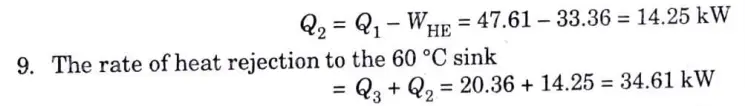
c. Write down the first and second T-dS equations and derive the expression for the difference in heat capacities, Cp and Cv.
Ans. A. Tds Equations:
1. The first Tds equation,
and second Tds equation,
2. At absolute zero temperature, T = 0 K ·
3. Putting T = 0 K in eq. (3.15.1) and (3.15.2),
Tds = CvdT … (3.15.3)



B. Expression for DIfference in Heat Capacities:
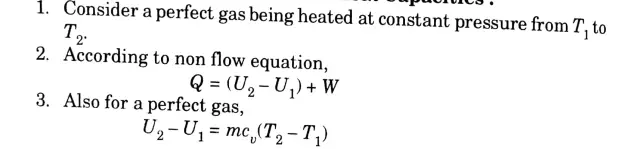
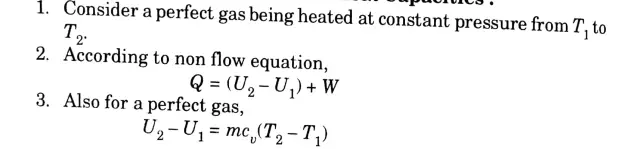
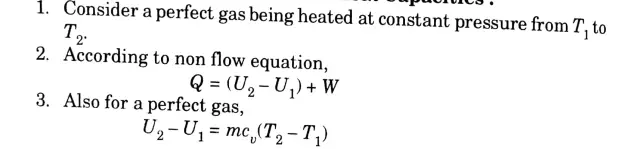



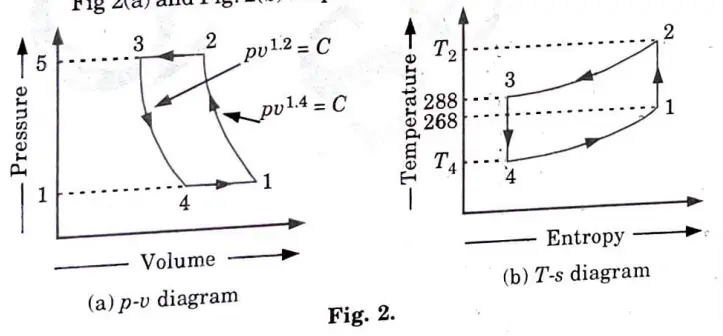
e. The atmospheric ·air pressure 1 bar and temperature – 5 °C is drawn in the cylinder of the pressure of 5 bar. In the cooler the compressed air is cooled to 15 °C, pressure remaining the same. It is then expanded to a pressure of 1 bar in an expansion cylinder from where it is passed to the cold chamber. Calculate
i. The work done per kg of air
ii. COP of the plant
For air assume law for expansion pv1.2 =constant:
Law for compression is pv1.4 = constant
Specific heat of the air at constant pressure is 1 kJ/kg-K
Ans.
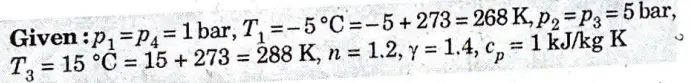
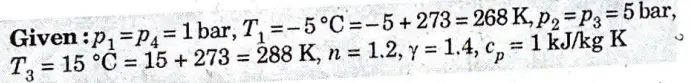
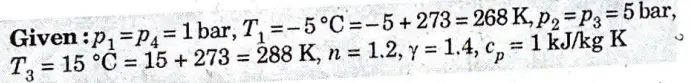
1. The p-v and T-ss diagrams for the given problem are shown in Fig 2(a) and Fig. 2(b) respectively.


2. For process 1-2,
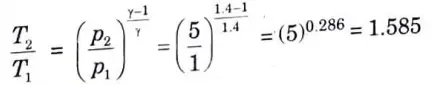
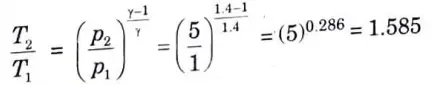
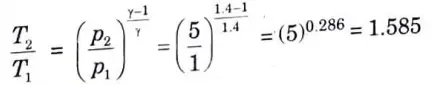
4. We know that work done by the compressor dw·ing the isentropic process 1-2 per kg of air,
5. Work done by the expander during the process 3-4 per kg of air,
7. We know that heat absorbed during constant pressure process 4- 1 per kg of air,
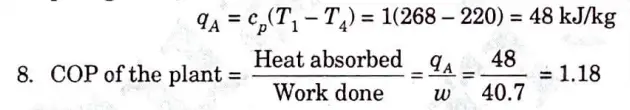
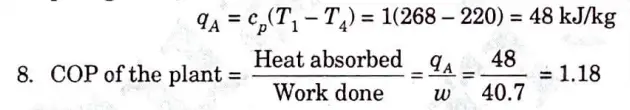
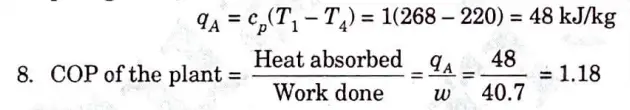
Section C : Thermodynamic last year Question Paper (Long Questions)
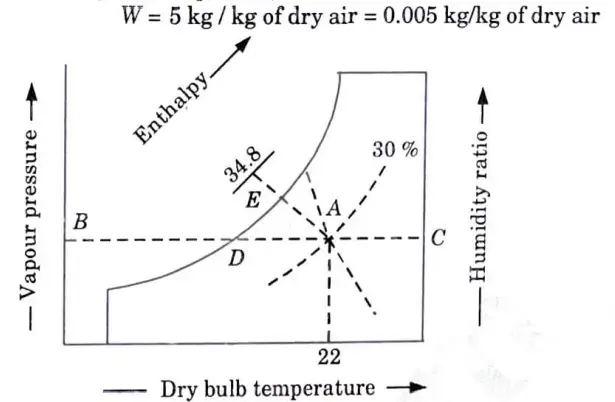
b. For a sample of air having 22° DBT, relative humidity 30 % at barometric pressure of 760 mm of Hg calculate :
i. Vapour pressure ii. Humidity ratio
iii. Vapour density and iv. Enthalpy
Verify your results by psychrometric chart.
Ans.
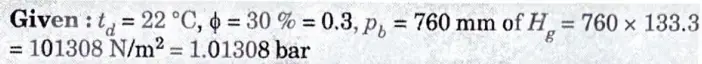
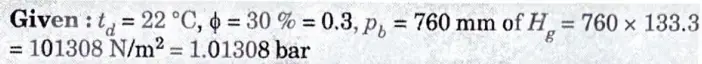
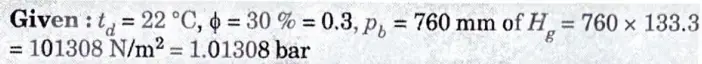
1. From steam tables, we find that the saturation pressure of vapour corresponding to dry bulb temperature of 22 °C is






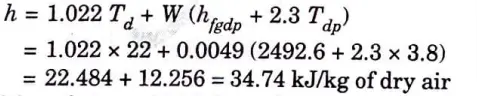
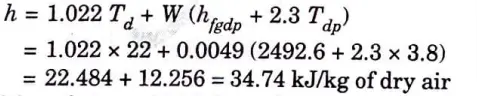
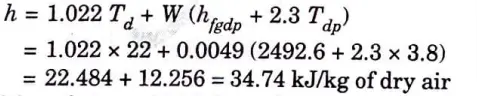
7. The initial condition of air i.e., 22 °C dry bulb temperature and 30 % relative humidity is marked on the psychrometric chart at point A as shown in Fig. 3.
8. From point A, draw a horizontal line meeting the vapour pressure line at point B and humidity ratio line at C.
9. From the psychrometric chart, we find that vapour pressure at point B,



And humidity ratio at point C





a. Stem at 20 bar 360 °C is expanded in a steam turbine to 0.08 bar. It then enters a condenser, where it is condensed to a saturated liquid water. The pump feeds back the water into the boiler
i. Assuming ideal processes, find the per kg of steams of the net work and the cycle efficiency
ii. If the turbine and the pump have each 80 % efficiency, find the percentage reduction in the network and cycle efficiency.
Ans. Given: p1 = 20 bar, T1 = 360 °C, p2 = 0.08 bar
To Find: i. Net work and cycle efficiency.
ii. Percentage reduction in net work and cycle efficiency.
1. From steam tables
At 20 bar and 360 °C
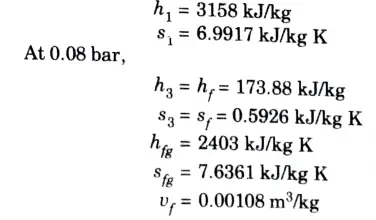
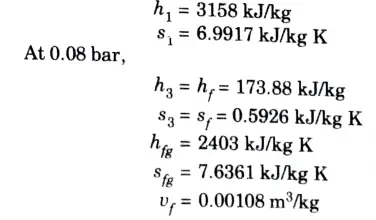
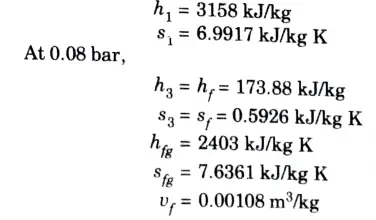
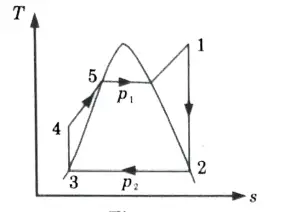


2. Since process 1-2 is isentropic,



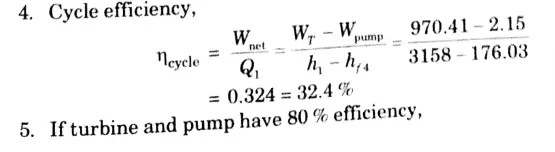
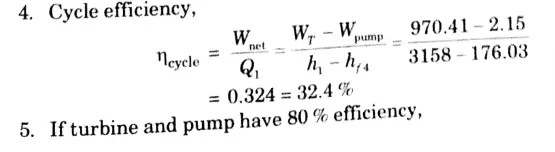
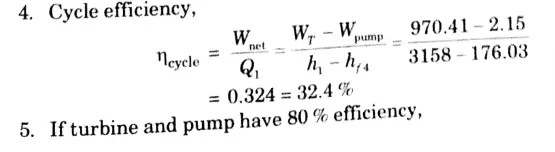



b. Prove that : Cp – Cv = – T(∂V / ∂T)2T (∂P / ∂V)T
Ans. We know that,
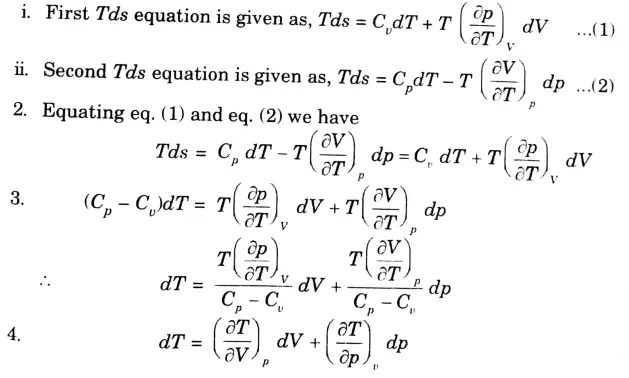
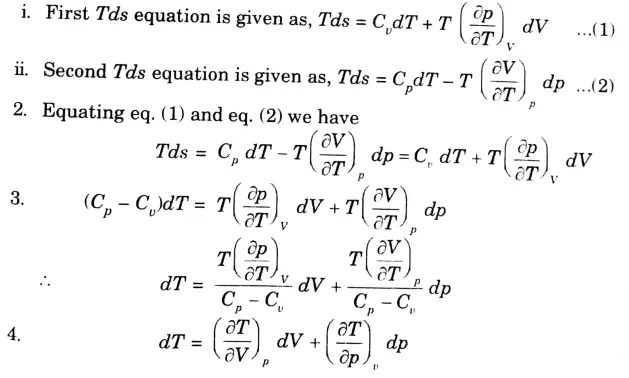
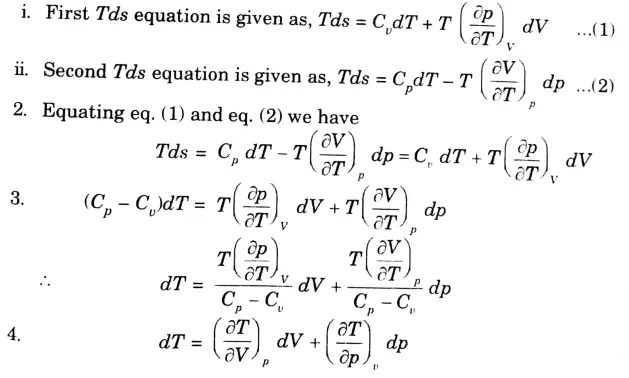
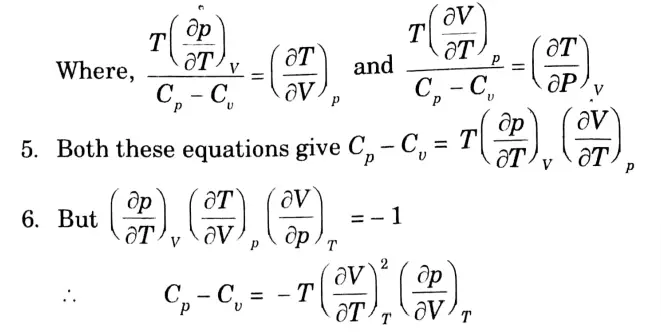
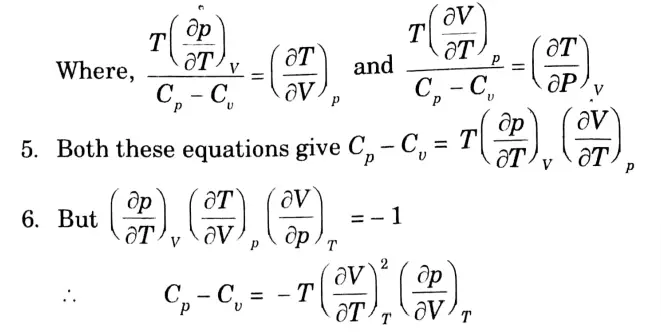
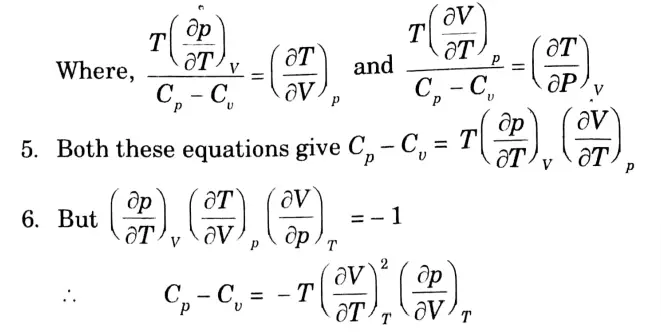
a. State the Clapeyron equation and discuss its importance during phase change of pure substance. Derive the equation of Clausius-Clapeyron equation for evaporation of liquids.
Ans. 1. One such equation that is utilised to ascertain the enthalpy change connected to a phase change is the Clausius-Clapeyron equation.
2. Consider the Maxwell relation,
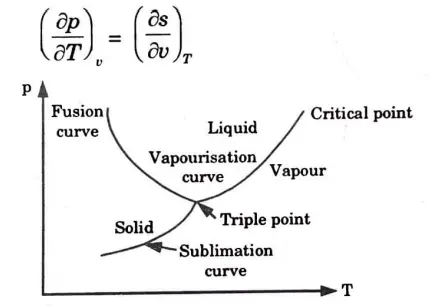


3. During the phase change the pressure is the saturation pressure, which depends on the temperature. Therefore the partial pressure derivative (dp/dT) is expressed by



4. During this process the pressure also remains constant.






5. Which is called the Clapeyron equation.
6. The Clapeyron equation is applicable to any phase change process that occurs at constant pressure and temperature. It can be expressed by following relation in general form,
Where 1 and 2 shows the two phases.
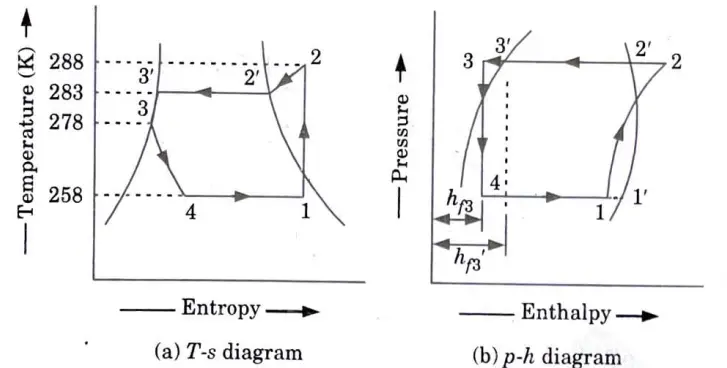
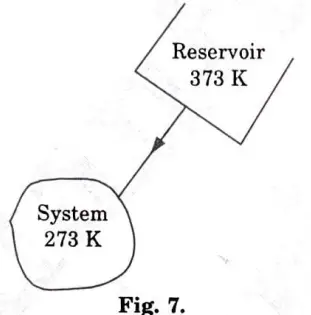
A vapour compression refrigeration system uses R-12 refrigerant, and the liquid evaporates in the evaporator at – 15 °C. The temperature of this refrigerant at the delivery from the compressor is 15 °C when the vapour is condensed at 10 °C. Find the coefficient of performance
i. If there is no under cooling and
ii. The liquid is cooled by 5 °C before expansion by throttling.
Ans.
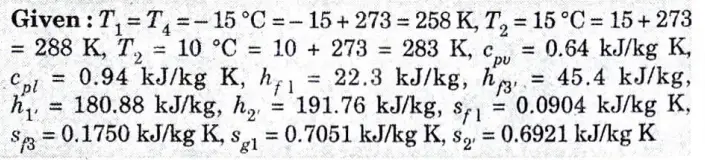
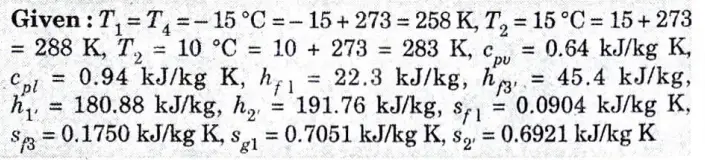
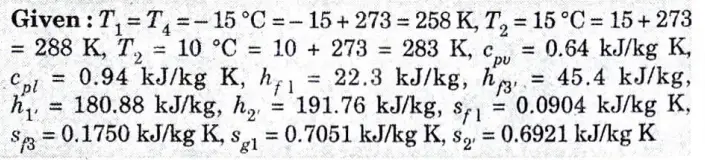
1. The T-s and p-h diagrams, when there is no undercooling are shown in Fig. 4(a) and Fig. 4(b) respectively.
2. We know that entropy at point 1,
4. Since the entropy at point 1 is equal to entropy at point 2, therefore
4. Since the entropy at point 1 is equal to entropy at point 2, therefore





a. Draw a neat diagram of lithium-bromide water absorption system and explain its working. List the major field of applications of this system.
Ans. A. Lithium-Bromide System :
1. Water serves as the refrigerant and lithium-bromide salt serves as the absorbent in a lithium-bromide absorption system.
2. Due to its extremely low pressure, the lithium-bromide solution exhibits a great affinity for water vapour.
3. Because water serves as the refrigerant, the operating temperature of the refrigerant in the evaporator must be higher than the freezing point of water.
4. Because lithium-bromide solution is corrosive, it is frequently employed to protect the metal components of the system against corrosion.
B. Construction of Lithium-Bromide Absorption System :
1. Since the absorber and evaporator work at roughly the same pressure, they are both contained in a single cylindrical shell.
2. Because the working pressures of the generator and condenser are nearly identical, they are both encased in another cylindrical shell.
3. The absorber has a charge of lithium-bromide solution, and the evaporator contains refrigerant (water).
C. Working of Lithium-Bromide Absorption System :
1. The chilled water tube bundle travels through the evaporator part of the shell carrying the water to be cooled. The solution pump pumps the solution from the absorber to the generator.
2. Cooling tower water is circulated by water tube bundles that pass through the absorber and condenser sections.
3. To cool the refrigerant vapour, a tube bundle circulates cooling tower water through the generator shell’s condenser section.
4. The evaporator pump sprays refrigerant water through nozzles onto the chilled water tube bundle.
5. To increase the cycle efficiency, a heat exchanger is also included.
D. Applications of Lithium-Bromide Absorption System :
1. Air conditioning. 2. Chilling of drinking water.
3. Chilling of beverages. 4. Chilling of fruit juices.
b. i. One kg of water at 273 K is brought into contact with a heat reservoir at 373 K. When the water has reached 373 K, find the entropy change of the water of the heat reservoir and of the universe.
ii. If the water is heated from 273 K to 373 K by first bringing it in contact with a reservoir at 323 K and then with a reservoir at 373 K, what will the entropy change of the universe be?
iii. Explain how water might be heated from 73 to 373 K with almost no change in the entropy of the universe.
Ans. 1. Water is being heated through a finite temperature difference Fig. 7.
2.The entropy of the water would rise while that of the reservoir would fall, resulting in a net increase in entropy for both the water (system) and the reservoir as a whole.
3. Water is being heated irreversibly, and to find the entropy change of water, we have to assume a reversible path between the end states which are at equilibrium,
7. When water is being heated from 273 K to 373 K,





10. The net entropy change of the universe would be zero and the water would be heated irreversibly if it were heated in infinite steps by bringing it in contact with an infinite number of reservoirs successively, so that at any instant the temperature difference between the water and the reservoir in contact is infinitesimally small.
a. A gas undergoes a thermodynamic cycle consisting of the following:
i. Process 1-2 is isochoric heat addition of 325.235 kJ/kg.
ii. Process 2-3 adiabatic expansion to its original pressure with loss of 70 kJ/kg in internal energy.
iii. Process 3-1 isobaric compression to its original volume with heat rejection of 200 kJ/kg
Prepare a balance sheet of energy quantities and find the overall changes during the cycle.
Ans.
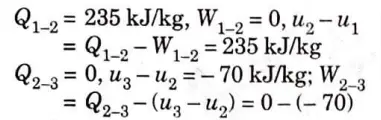
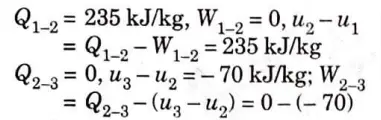
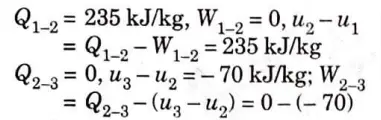
This cycle is known as Lenoir cycle, and the operation of pulse jet approximates to it.
b. Show that the Kelvin-Planck and the Clausius statement of the second law of thermodynamics are equivalent.
Ans. A. Kelvin-Planck Statement: It is impossible to build a heat engine that runs in a cycle and generates no effects other than work output and heat exchange with a single heat reservoir, claims this statement.
B. Equivalence of Kelvin-Plank and Clausius Statements:
1. Although the claims made by Clausius and Kelvin Planck seem to be in opposition to one another, they are actually related and mutually supportive.
2. It is possible to demonstrate that these two claims are equivalent by demonstrating how breaking one of them results in breaking the other and vice versa.
a. Violating Kelvin Planck Statement Leads to Violation of Clausius Statement:
1. Let’s consider a heat engine which violates Kelvin Planck statement by absorving heat from source at T1 and converts it completely into work.
∴ W = Q1
2. Now let’s introduce a refrigerator which gets work input from the engine.
3. The refrigerator extracts Q2 from the low temperature heat reservoir and rejects heat Q1 + Q2 to high temperature heat reservoir.4. Combining the engine the refrigerator into one system working between same temperature limits, we observe that the sole effects of combined system is to transfer Q2 from low temperature heat rservoir T2 to high temperature heat reservoir without any work input thus violating the Clausius statement Fig.
b. Violation of Clausius Statement Leads to Violation of Kelvin Planck Statement:
1. Let’s consider a refrigerator which violates Clausius statement as shown in the Fig.
2. Refrigerator absorbs heat Q2 from low temperature heat reservoir and rejects the same to the high temperature reservoir without the aid of any external work i.e., W = 0
3. Let’s introduce a heat engine which receives heat Q1 (Q1>Q2) from the high temperature reservoir and rejects heat Q2 and produces work,
W = Q1 – Q24. Now combining the refrigerator and heat engine into one system. We observe that the combined system operates as a heat engine, which receives heat from a single high temperature reservoir as Q1 -Q2 and converts the same into equal amount of work energy without any heat rejection.
5. This violates the Kelvin Planck statement of second law of thermodynamics.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Thermodynamics Quantum, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Thermodynamics Quantum PDF: | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |

1 thought on “Last year Thermodynamics question paper – AKTU Btech (Mechanical Engineering)”