With Quantum Notes, you can improve your structural analysis studies. Find essential, often asked questions for your Aktu Btech examinations. With our assistance, you can succeed in your academic endeavours! Unit-4 Rolling Loads and Influence Line Diagrams
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Structural Analysis: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. Define influence line diagram. What are the advantages of influence line and uses of it.
Ans. A. Influence Line Diagram:
- 1. An influence line diagram is a curve or graph that depicts the function, such as a response at a support, the shear force at a section, the bending moment at a section of a structure, etc., at various places of a unit load on the span of the structure.
- 2. The influence lines for bending moment, shear force, or stress are composed of straight lines for statically determinate structures, but they are curved for statically indeterminate structures.
B. Advantages of Influence Lines: Following are the advantages of influence lines :
- 1. However, the fluctuation of the shear and bending moment in the member is best characterized using the influence line if a structure is subjected to a live load or moving load.
- 2. After constructing the influence line, it is simple to see where the moving load should be put on the building to ensure that it has the greatest influence at the designated position.
- 3. The ordinates of the influence line diagram can be used to determine the size of the related reaction, shear, moment, or deflection at the point.
- 4. In designing bridges, industrial crane rails, conveyors, and other structures where loads flow across their span, influence lines are crucial.
C. Uses of Influence Lines: Following are the uses of influence lines:
- 1. Influence lines are used to illustrate how shear force and bending moment vary within a member that is being loaded or moved.
- 2. Influence lines provide guidance on where to place a moving load on a structure to maximize its influence at a given moment.
- 3. The magnitude of the related reaction, shear, moment, or deflection at the location can be estimated using the ordinates of influence line diagram.
- 4. When designing the structures that support the loads that move across the span, influence lines are used. The design of bridges, industrial crane rails, and conveyors, among other types of structures, are prevalent.
Q2. A uniformly distributed load of 10 kN/m intensity covering a length of 2m crosses a simply supported beam of span 8m. Determine the maximum positive shear force, maximum negative shear force and maximum bending moment at a section 3m from left support.
Ans.
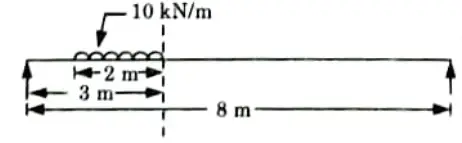


1. ILD for Shear Force:
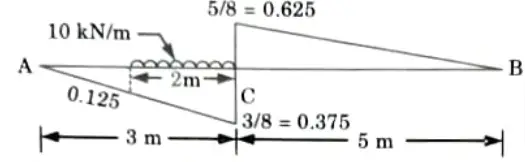


i. Maximum negative shear force occurs when the load is applied as shown in Fig. on AC.
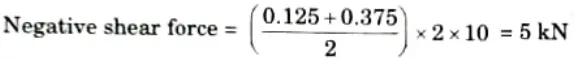
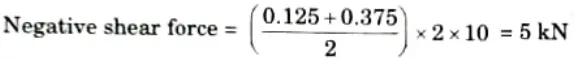
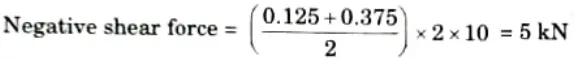
ii. Maximum positive shear force occurs, when load applied as shown in Fig.
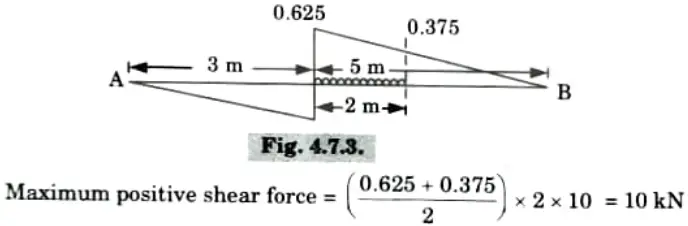


2. Maximum Bending Moment:
i. The load should be so arrange that the section divides it in the same ratio as it divides the span.
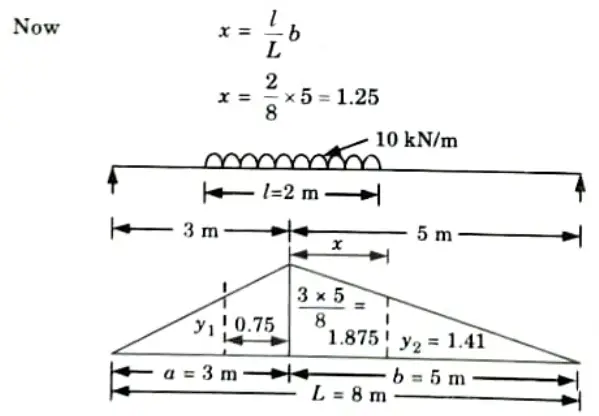


ii. From property of similar triangle :
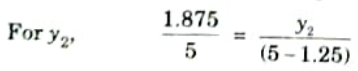
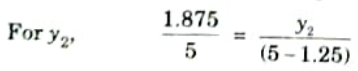
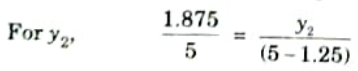
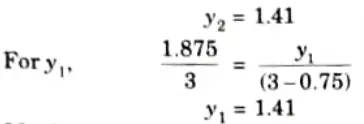
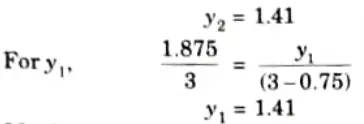
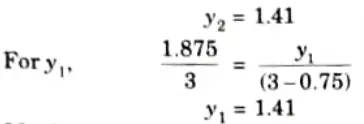
iii. Maximum bending moment,
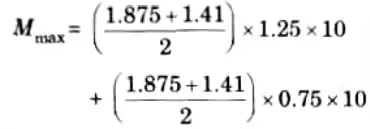
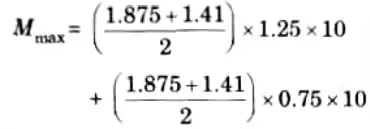
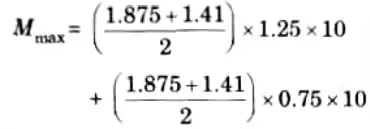
Maximum bending moment,
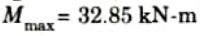
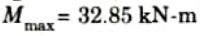
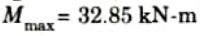
Q3. What do you understand by the term rolling loads ?
Ans.
- 1. Rolling Loads (or Moving Loads): In actual fact, we frequently deal with moving loads or positions that are subject to change.
- 2. Example: Axle loads of moving trucks or vehicles, wheel loads of a railway train or wheel loads of a gantry assembly on a gantry girder etc.
- 3. When a load is rolling or moving, it’s important to calculate the maximum shear force and bending moment at various points along the load’s path.
Q4. Discuss Muller-Breslau’s principles and its application in structural analysis.
Ans. The Muller-Breslau principle is a method that Muller-Breslau created for quickly constructing the shape of an influence line.
- 1. Muller-Breslau’s Principle: This concept states that “when the function acts on the beam, the influence line for the function (reaction, shear, or moment) is to the same scale as the deflected shape of the beam.”
- 2. Applications in Structural Analysis:
- i. The Muller-Breslau concept offers a rapid approach for determining the influence line’s form.
- ii. The ordinates at the peaks can be obtained using the basic method after the form of the influence line is known.
- iii. It is possible to locate the live load on the beam using the shape of the influence line, and then use statics to calculate the maximum value of the function (shear or moment).
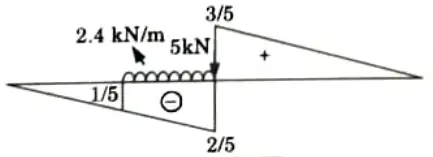
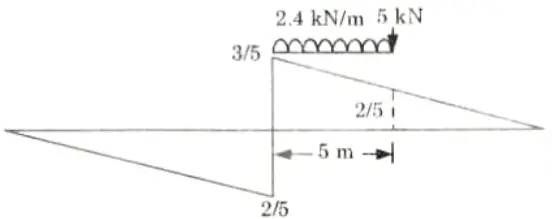
Q5. A simply supported beam has a span of 25 m. Draw the influence line for shearing force at a section 10 m from one end and using this diagram determine the maximum shearing force due to the passage of a point load 5 kN followed immediately by uniformly distributed load of 2.4 kN/m extending over a length of 5 m.
Ans. Given: Span of beam, L = 25 m, Distance of a section, x = 10 m
Point load, W= 5 kN, Intensity of UDL, w = 2.4kN/m
Length of UDL = 5 m
To Find: Maximum shear force.
1. ILD for shear force at section at a distance 10 m from left support is shown in Fig.
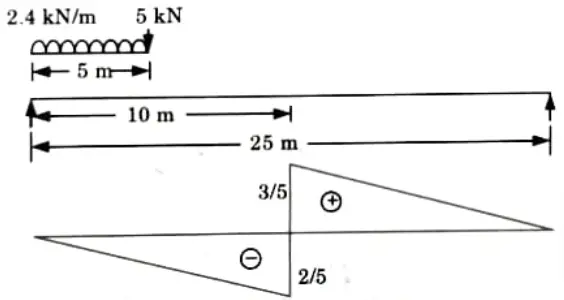


2. Maximum Negative Shear Force: For the maximum negative shear force placed the load in left part of section as shown in Fig.


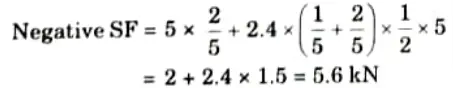
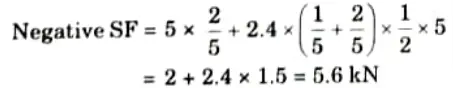
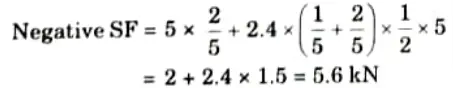
3. Maximum Positive Shear Force:
For the maximum positive shear force placed the load in right side of section on LD of shear force as shown in Fig.


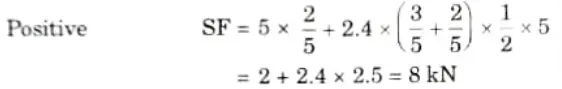
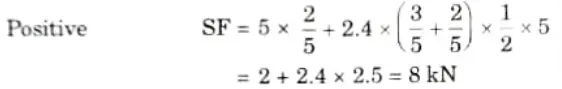
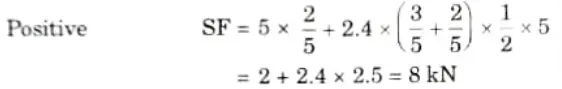
Q6. Uniformly distributed load of intensity 30 kNm crosses a simply supported beam of span 60 m from left to right. The length of UDL is 15 m. Find the value of maximum bending moment for a section 20 m from left end. Find also the absolute value of maximum bending moment and shear force in the beam.
Ans. Given: Span of beam, L = 60 m, Length of UDL, l = 15 m
Intensity of UDL, w = 30 kN/m, Distance of section, x = 20m
To Find: BM at section, Absolute BM and shear force.
A. Maximum Bending Moment at Given Section:
1. LD for bending moment at given section, as shown in Fig.
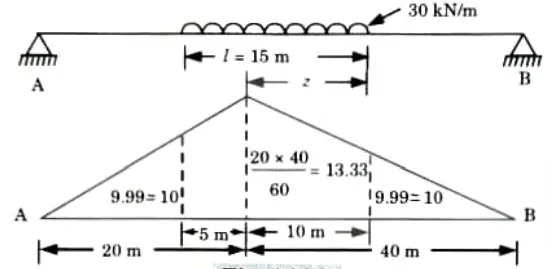


2. Condition for maximum bending moment,
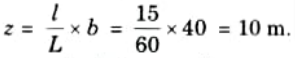
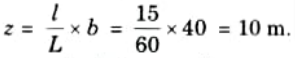
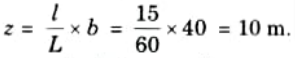
3. Maximum bending moment at given section.



B. Absolute Maximum Bending Moment:
1. The absolute maximum bending moment occurs at the centre of the span when the loading is symmetrically placed on the span.
2. LD for absolute value of maximum bending moment, as shown in Fig.
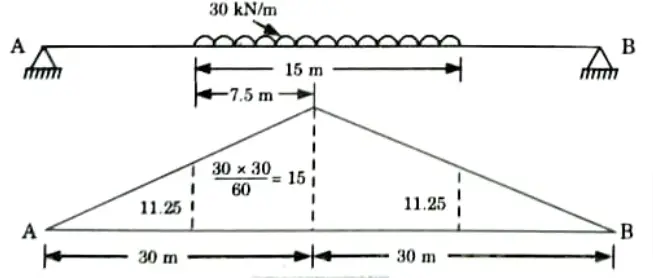


3. Maximum bending moment,
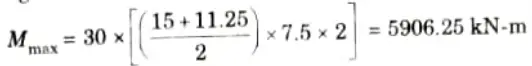
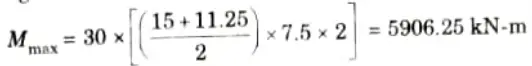
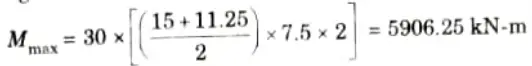
C. Absolute Value of Shear Force:
1. Positive Shear Force :
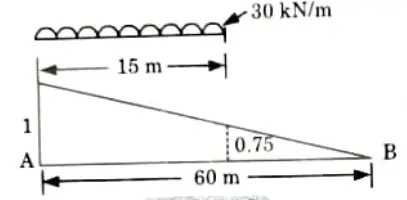


i. For maximum positive shear force the load should be placed as shown in Fig.



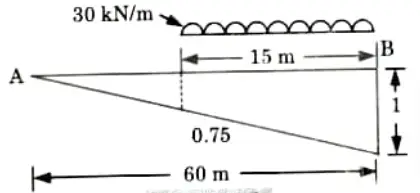
2. Negative Shear Force:
i. For maximum negative shear force the load should be placed as shown in Fig.








Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Structural Analysis Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Structural Analysis Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
