Quantum Notes can help you succeed in your structural analysis coursework. Prepare for your Aktu Btech examinations by learning important, commonly asked questions. With our assistance, you may succeed academically! Unit-3 Strain Energy and Deflection of Beams
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Structural Analysis: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. Define the term strain energy or resilience of the member. Deduce the strain energy expression for the following cases:
1. Strain energy stored in a member due to axial loading.
2. Strain energy stored in a member due to bending.
3. Strain energy stored in a beam subjected to a uniform bending moment.
Ans. A. Strain Energy:
- 1. An elastic member has energy stored in it when it is deformed by an external loading until it reaches its elastic limit; this energy is known as the strain energy of the member or the member’s resilience.
- 2. The quantity of work performed by the external force to cause the deformation is equal to the strain energy of the deformed member.
B. Expressions for Strain Energy:
1. Strain Energy in a Member due to Axial Loading:
- i. Consider an elastic member of length L and cross-sectional area A subjected to an external axial load W.
- ii. The extension in the member is 𝛿, as the load is gradually applied so the magnitude of load is increased from 0 to W.
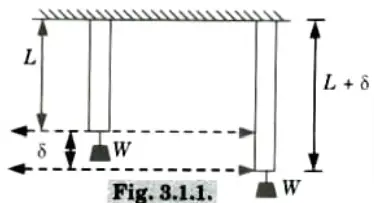


- iii. Strain energy = External work done by the load



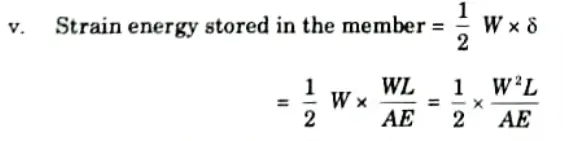
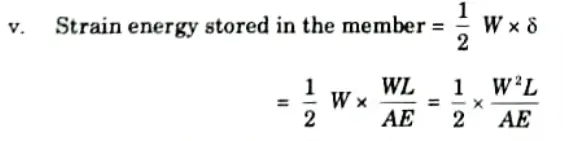
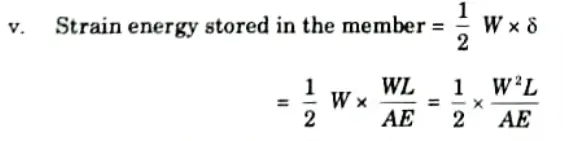
- vi. Strain energy stored in the member per unit volume
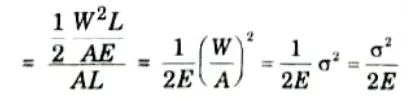
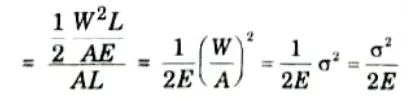
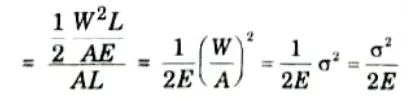
2 Strain Energy Stored in a Member due to Bending:
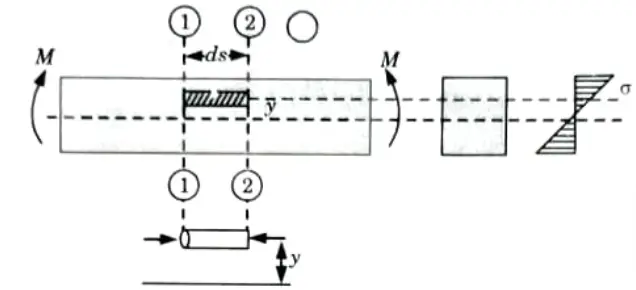


- i. A beam shown in the Fig.is subjected to a uniform moment M.
- ii. Let an elemental length ds of the beam between two section 1-1 and 2 2 having elementary length ds.
- iii. The elemental length of the beam may be considered as consisting of an infinite number of elemental cylinders each of area da and length ds.
- iv. Considering a cylindrical element at y distant from the neut ral layer between the sections 1-1 and 2-2.
Intensity of stress in the elemental cylinder,
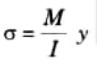
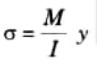
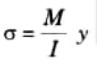
I = Moment of inertia of the entire section of beam about the neutral axis.
v. Energy stored by the elemental cylinder = Energy stored per unit volume x Volume of the cylinder
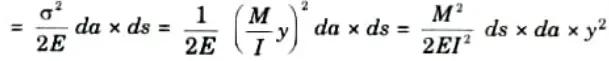
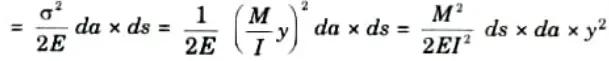
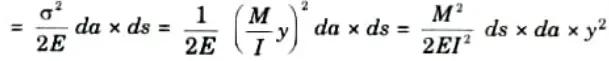
vi. Energy stored by the element ds = Sum of the energy stored by each elemental cylinder between the sections 1-1 and 2-2.
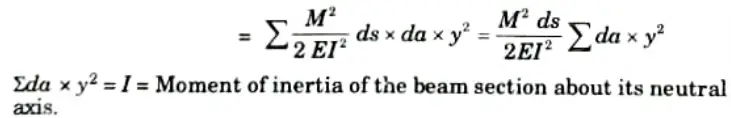
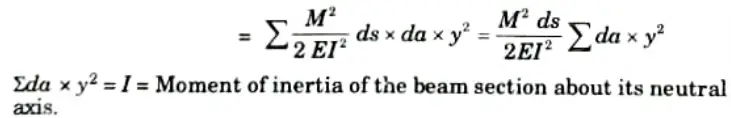
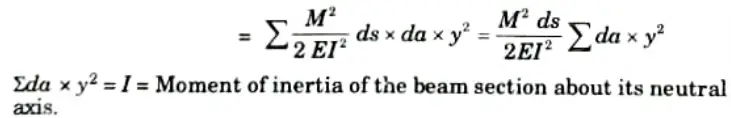



3. Strain Energy Stored in a Beam Subjected to a Uniform Bending Moment:
i. For constant bending moment M, the strain energy
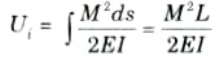
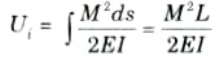
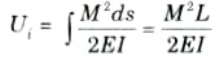
ii. If the beam section is rectangular with width b and depth d and the beam is subjected to uniform bending moment M,
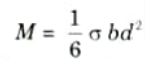
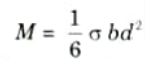
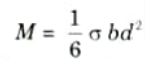
Where 𝜎 is the extreme bending stress for each section
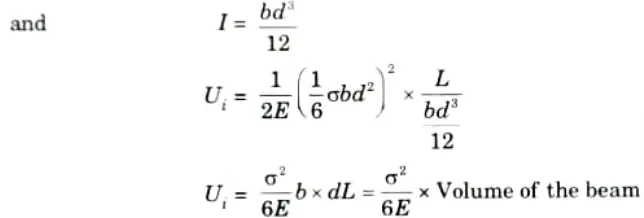
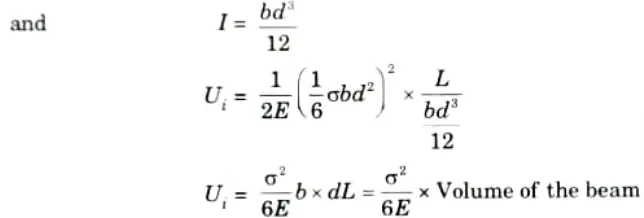
Q2. Determine the horizontal displacement of the roller end D of the portal frame shown in Fig. El is 8000 kN-m2 throughout.
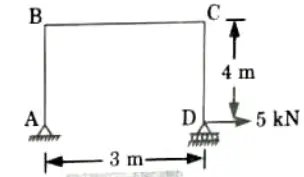


Ans. Given: Load = 5 kN, EI = 8000 kN-m2
To Find: Horizontal displacement at D.
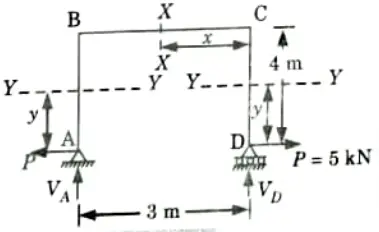





VA = 0
4. Expression for Moments:
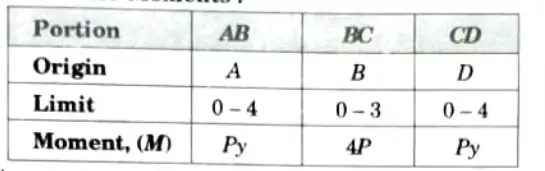


5. Strain energy stored by the frame,
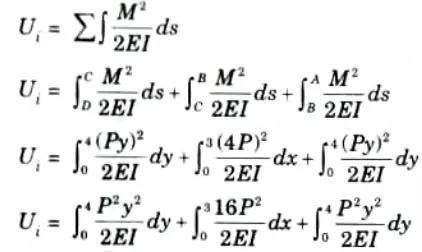
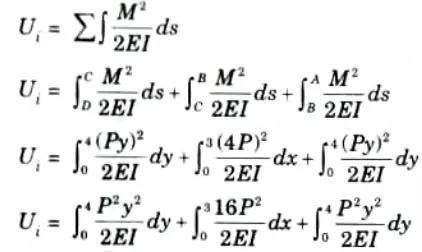
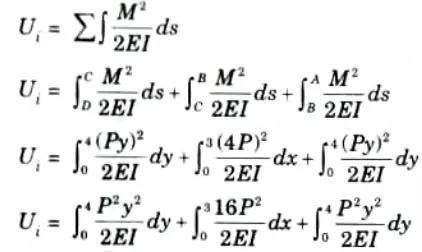
6. Horizontal displacement at D is given by,



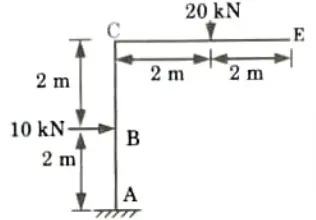
Q3. Determine the horizontal and vertical deflection at point E of the frame shown in Fig. Take EI as constant.
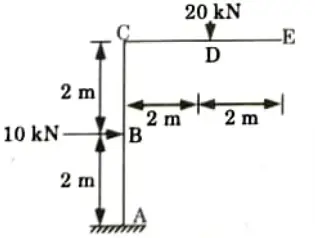


Ans. Given: Loads = 20 kN and 10 kN
To Find: Horizontal and vertical deflection at point E.


1. Expression for Moments:
Considering sagging moment as positive.
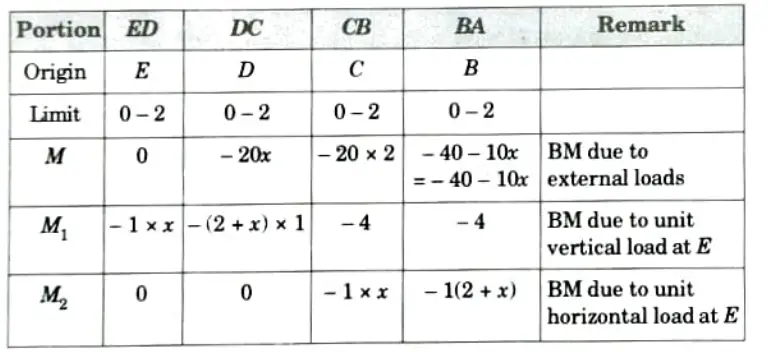


2. Vertical Deflection at E:






3. Horizontal Deflection at E:



Q4. Determine the deflection at free end of a cantilever beam.
Ans. 1. Consider a cantilever beam AB of length L carrying a point load Wat free end.



2. Bending moment diagram for cantilever is shown in Fig.
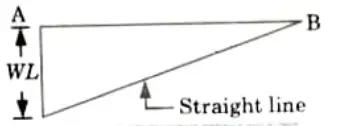


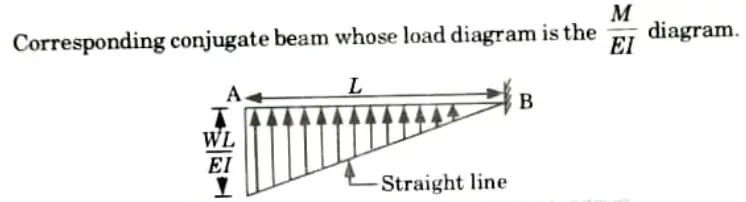


3. Slope at Free End in Cantilever Beam:
Slope at B for the given beam = Shear force at B for conjugate beam.
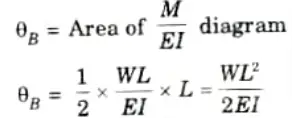
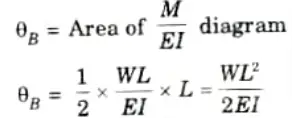
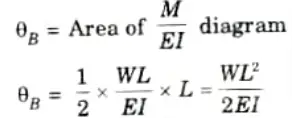
4. Deflection at Free End in Cantilever Beam:
Deflection at B for the given beam = BM at B for conjugate beam.
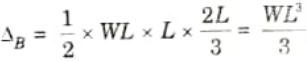
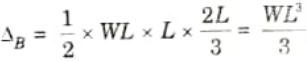
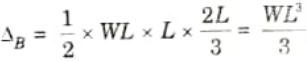
Q5. Determine the slope at the supports and deflection at the mid span of a simply supported beam AB of span L subjected to a point load W at the mid span. Take El as constant. Use any method of your choice.
Ans. Given: Concentrated load = W, Span of beam = L.
To Find: Deflection at mid span and slope at supports.
- 1. Fig.(a) shows the real beam; BM diagram for the real beam is shown in the Fig.(b).
- 2. The M/EI diagram of the real beam becomes the elastic weight or loading for the conjugate beam. The conjugate beam A’C’B’ (corresponding to the real beam ACB) with the loading is shown in Fig.(c).
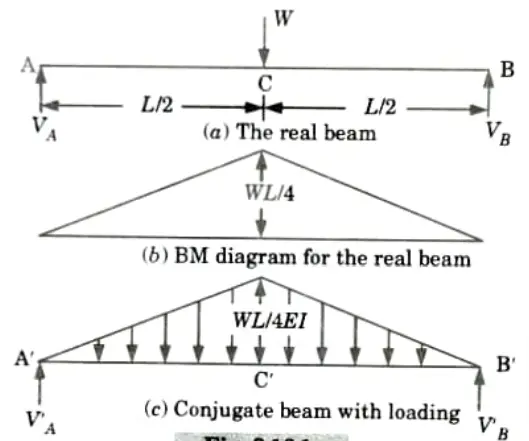


- 3. For the conjugate beam:
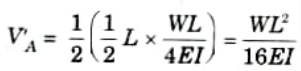
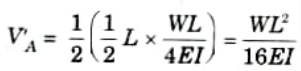
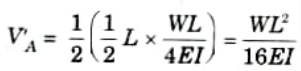
- 4. But shear at any section of the conjugate beam is equal to the slope of the real beam.
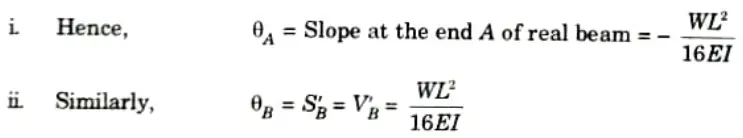
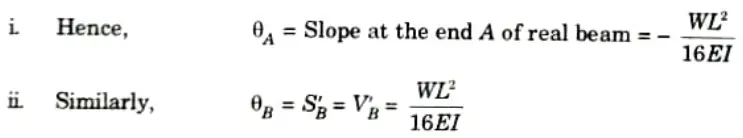
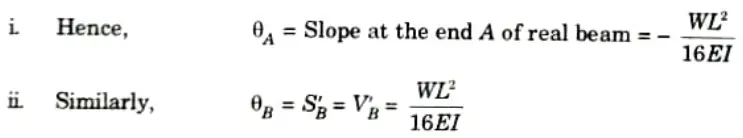
- 5. Again, for the conjugate beam,
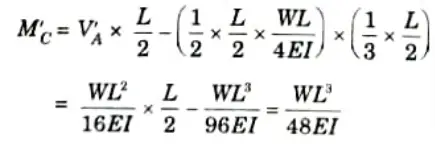
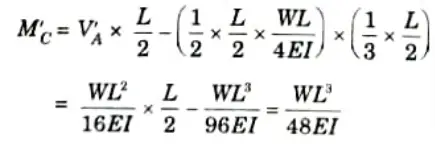
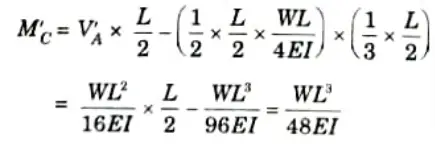
- 6. But the BM at any section of the conjugate beam is equal to the deflection of the real beam.
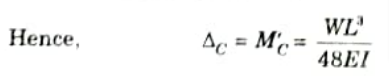
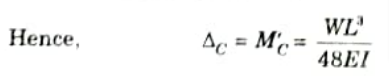
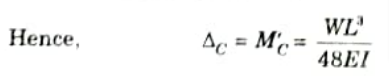
Q6. A simply supported beam of span 8m is subjected to a point load of 150 kN at 5 m from left support. Using the conjugate beam method, determine the slope at the supports and deflection under the load. Take El as constant.
Ans. Given: Span of beam, L = 8 m, Point load, W= 150 kN
To Find: Slope at the supports and deflection under the load.
1. Reaction at Supports,
i. Taking moment about B,
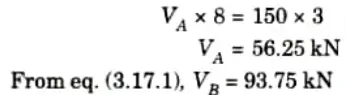
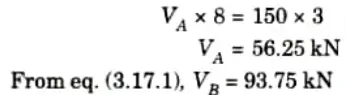
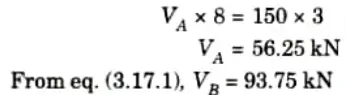
ii. Draw the conjugate beam diagram.
Bending moment at distance 3 m from support B
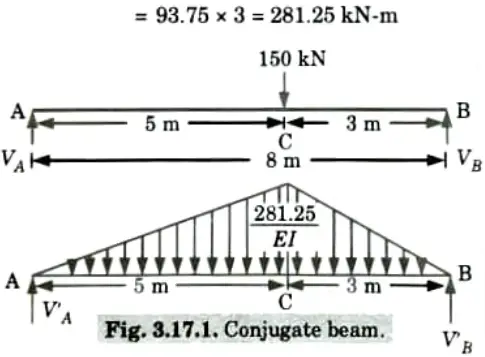


iii. Total load on the conjugate beam,
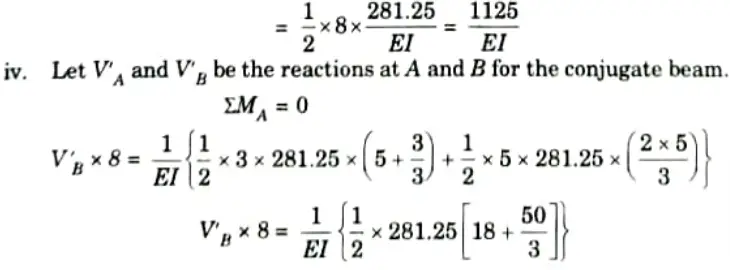
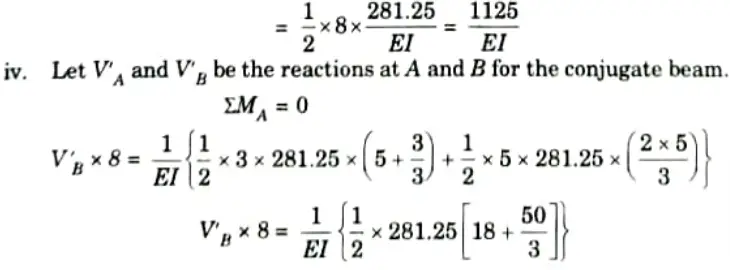
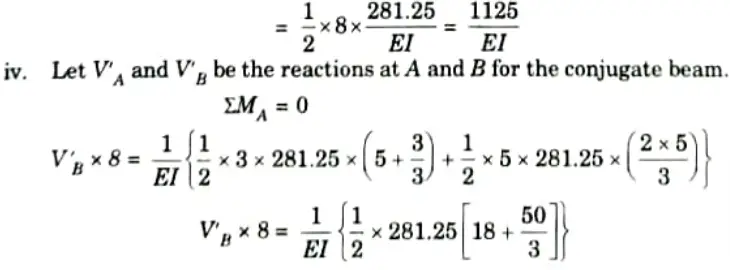



3. Slope at Supports:



4. Deflection at C:
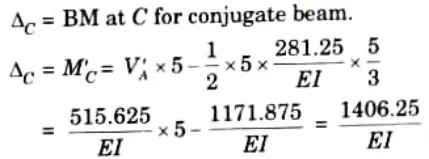
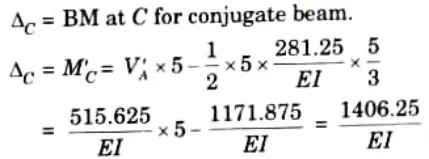
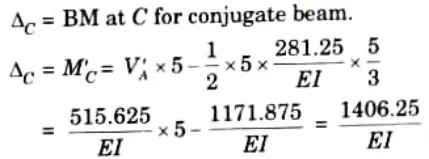



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Structural Analysis Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Structural Analysis Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
