Learn about Structural Analysis Short Question Notes for the B.Tech. AKTU Quantum Book. Learn the fundamentals of analysing and designing structures for reliable and effective building projects.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Structural Analysis: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Unit-I: Classification of Structures (Short Question)
Q1. Define the term structure.
Ans. A structure is a connected set of pieces used to support a load. Buildings, bridges, and towers are all examples of structures in civil engineering.
Q2. What are the different types of structures ?
Ans. Classification of Structure :
- i. On the Basis of Structural Forms and Shapes:
- a. Linear forms (skeletal structures), and
- b. Curvilinear forms (surface structures).
- ii. On the Basis of Dominant Stress Conditions:
- a. Uniform stress forms, and
- b. Varying stress forms.
- iii. On the Basis of Complexity of their Force Analysis :
- a. Beams and trusses,
- b. Cables and arches,
- c. Frames, and
- d. Surface structures.
Q3. Define structural load.
Ans. The forces, deformations, or accelerations applied to a structure or its components are referred to as structural loads. Loads induce structural strains, deformation, and displacements.
Q4. What are the different types of structural load?
Ans. The different types of struçtural loads are:
i Dead load, ii. Live load,
iii Impact load, iv. Cyclic load,
v. Environmental loads, like:
a. Wind load, b. Snow, rain and ice loads,
c. Seismic load, d. Thermal load,
e. Ponding load, and f. Frost heaving.
vi. Other loads:
a. Foundation settlement, b. Fire,
c. Corrosion, d. Creep or shrinkage.
Q5. Discuss the structural elements.
Ans. The common structural elements are as follows :
- i. Tie Rods or Bracing Struts: Tie rods are the structural members subjected to tensile force.
- ii. Beams: Beams are usually straight horizontal members used primarily to carry vertical loads.
- iii. Columns: Columns are usually vertical and resist axial compression.
Q6. Define the term framework.
Ans. It is the skeleton of the entire construction, and it securely and inexpensively supports all intended loads.
Q7. Mention any three reasons due to which sway may occur in portal frames.
Ans. Sway in portal frames may occur due to:
- i. Unsymmetry in geometry of the frame,
- ii. Unsymmetry in loading.
- iii. Settlement of one end of a frame.
Q8. Describe the static indeterminacy with example.
Ans. Static Indeterminacy : There are three conditions of static equilibrium i.e., 𝚺Fx = 0, 𝚺Fy = 0 and 𝚺M = 0. If a structure can be analyzed just by using these three conditions of equilibrium, then it is a statically determinate structure otherwise it is called as statically indeterminate structure.
Example: Fixed beam with general loading.
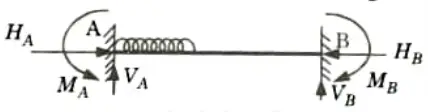


Total number of unknowns = 6
Number of equations available = 3
Static indeterminacy = 6 – 3 = 3
Q9. Describe the kinematic indeterminacy with example.
Ans. Kinematic Indeterminacy: As a structure is loaded, each joint experiences displacements in the form of translations and rotations. The number of uncertain joint displacements in a structure is referred to as its kinematic indeterminacy.
Example:



Here support A is fixed, hence cannot have any displacement whereas support B is on rollers and hence have two degrees of freedom i.e., horizontal translation and rotation.
Q10. Which method of analysis is suitable, if static indeterminacy is more than kinematic indeterminacy ?
Ans. Stiffness method is suitable, when static indeterminacy is more than kinematic indeterminacy.
Q11. State degree of freedom.
Ans. Degree of Freedom:
- i. When a structure is loaded, certain spots on it, known as nodes, will experience unknown displacements. These displacements are referred to as the structure’s degree of freedom.
- ii. Each node in 2-dimension can have no more than two linear displacements and one rotational displacement.
- iii. In three dimensions, each node on a frame or beam can only have three linear and three rotational displacements.
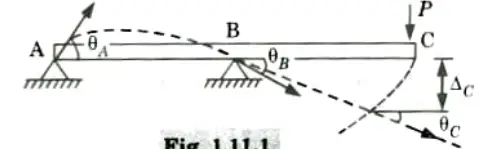
Example : In Fig.
- i. Number of nodes = 3 (A, B and C)
- ii. Here three rotational displacements like 𝚹A, 𝚹B and 𝚹C.
- iii. One vertical displacement and one horizontal displacement at C, as 𝚫C
- iv. Total number of displacements = Degree of freedom = 5


Q12. Differentiate between determinate and indeterminate structures.
Ans.
| S. No. | Determinate Structures | Indeterminate Structures |
| i. | Conditions of equilibrium are sufficient to analyze the structure completely. | Conditions of equilibrium are insufficient to analyze the structure completely. |
| ii. | No stresses are caused due to temperature changes. | Stresses are generally caused due to temperature variations. |
| iii. | No stresses are caused due to lack of fit. | Stresses are caused due to lack of fit. |
Q13. Give an example of a structure where it is externally as well as internally indeterminate.
Ans. Equilibrium conditions, e = 3
Total external reaction, r = 4
Number of member, m = 1
Number of joint, j = 6
i. External indeterminacy,
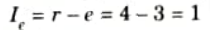
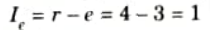
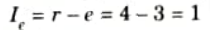
ii. Internal indeterminacy,
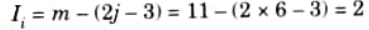
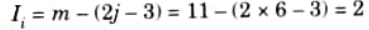
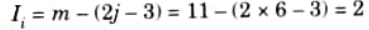
iii. Total indeterminacy,
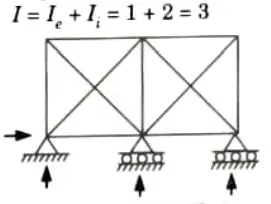


Q14. Discuss the cables.
Ans. Cables are utilised for both support and load transmission from one member to the next. A cable is a flexible tension part.
Q15. What is the expression for computing the length of a cable for horizontal span ‘L’ and central dip ‘h’ when both support are at same level ?
Ans.
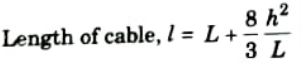
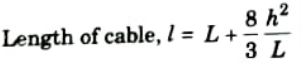
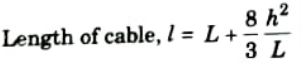
Q16. Write down the expression for length of cable, when supports are at different level.
Ans. Length of cable in this case is given by,
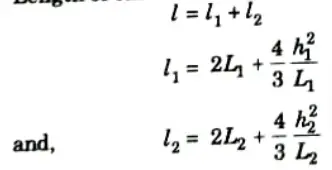
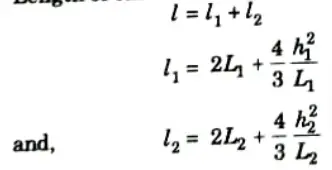
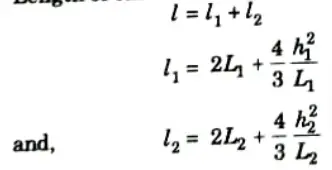
Q17. Give the expression for horizontal reaction and tension at ends of suspension cable.
Ans.
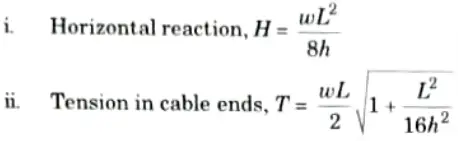
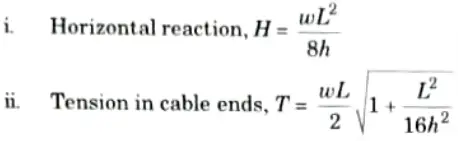
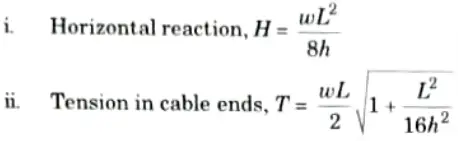
Q18. What do you understand by stability of plane truss ?
Ans. m = Number of members (or bars),
j = Total number ot joints, and
r = Number of reaction components.



Unit-II: Analysis of Trusses (Short Question)
Q1. Define truss.
Ans. The members of a truss are arranged in a geometric pattern. Only tensile or compressive force is applied to the members. As a result, a truss uses fewer materials to support a given load than a beam.
Q2. What are the various types of plane trusses ?
Ans.
- i. On the basis of utility of trusses:
- a. Roof truss, and
- b. Bridge truss.
- ii. On the basis of the geometrical configuration :
- a. Simple truss,
- b. Compound truss, and
- c. Complex truss.
Q3. Define space truss with suitable sketch.
Ans. Space trusses have members extending in three dimensions and are suitable for derricks and towers.
- i. Space truss consists of members joined together at their ends to form a stable three-dimensional structure.
- ii. The simplest element of a stable truss is a tetrahedron.
- iii. It is formed by connecting six members together with four joints.



Q4. Distinguish between plane and space truss.
Ans. Plane trusses are made up of members that all lie in the same plane and are commonly used for bridge and roof support, whereas space trusses feature members that extend in three dimensions and are used for derricks and towers.
Q5. Discuss different types of pin jointed determinate trusses.
Ans. Following are different types of these structures:
- Simple Truss: Simple truss, which is one of the most stable trusses, is one of the simplest versions of the truss framework.
- Compound Truss: It is necessary to join two or more simple trusses to make one stiff framework in structures such as factory or warehouse roof shades.
- Complex Truss: Complex trusses are those that do not meet the requirements of a perfect or compound truss but satisfy the statical determinacy criterion for the plane truss.
Q6. What do you mean by compound and complex space truss?
Ans. Compound Space Truss: A compound space truss is created by joining two or more simple trusses. Because it is less expensive to build a lighter compound truss than a heavier single simple truss, this form of truss is utilised to support loads acting over a long span.
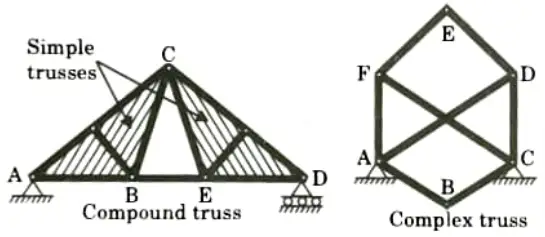


Complex Space Truss: Complex space truss is a truss that cannot be categorised as either simple or compound truss.
Q7. Discuss the method of section.
Ans. After identifying the support responses, a section line is constructed passing through no more than three members whose forces are unknown, resulting in the frame being split into two independent halves.
Under the action of loads, reactions, and forces in the components that cut by section line, each part should be in equilibrium.
Q8. What are the limitations of method of section ?
Ans. Following are the limitations of method of section:
- i. Section line cannot pass through more than three members.
- ii. It cannot separate the frame into more than three parts.
Q9. Illustrate the tension coefficient method for the analysis of space truss.
Ans. The tension coefficient method establishes a connection between the components of member forces along the coordinate axes and the member coordinates at the ends of members; this analysis yields linear simultaneous equations for the components of member forces along the coordinate axis at each joint. This approach provides member force per unit length rather than tension coefficient member forces.
Q10. What are the various types of supports?
Ans. The various types of supports are as follows:
i. Roller support, ii. Hinged support,
iii. Fixed support, iv. Link support,
v. Ball and socket support, and vi. Rigid support in space.
Q11. What is the criteria for classification of truss ?
Ans. Classification of trusses are based on following criteria:
- i. The shape of the upper and lower chords.
- ii. Type of web.
- iii. The condition of support.
- iv. Purpose of structure.
- v.The level of the floor (lane, road etc.).
Q12. What do you understand by external unstability ?
Ans. A structure is externally unstable if all of its reactions are concurrent or parallel. As shown in following Fig. (a), reactions V1, V2 and V,3 are concurrent and unstable. Hence, structure is externally unstable.
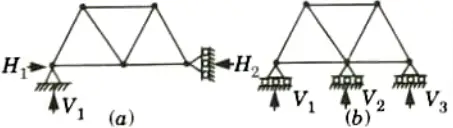


In Fig. (b), reactions V1, V2 and V3 are parallel and unstable Hence, this structure is also externally unstable.
Q13. Define fatigue.
Ans. A phenomenon that causes a material’s internal resistance to decrease when subjected to repetitive or fluctuating cyclic stresses below the material’s tensile strength.
Unit-III: Strain Energy and Deflection of Beams (Short Question)
Q1. Define the term strain energy or resilience of the member.
Ans. When an elastic member is deformed by an external loading to its elastic limit, some energy is stored in it; this energy is referred to as the strain energy of the member or the member’s resilience.
The deformed member’s strain energy is equal to the amount of work done by the external force to cause the deformation.
Q2. Write the expression of strain energy stored in a member due to axial loading.
Ans.
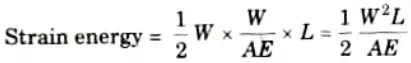
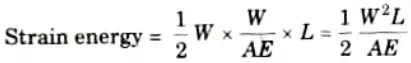
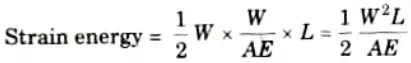
Q3. Write the expression of strain energy stored in a member due to bending.
Ans.
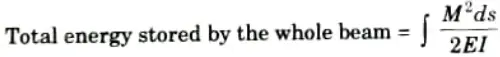
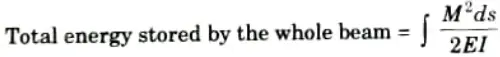
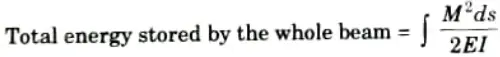
Q4. Write the expression of strain energy stored in a beam subjected to a uniform bending moment.
Ans. Strain energy stored by the beam,
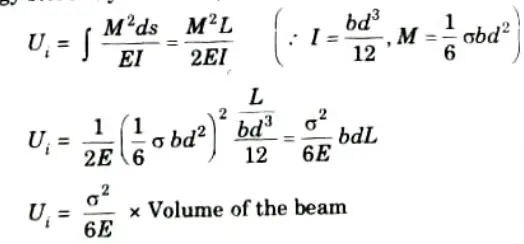
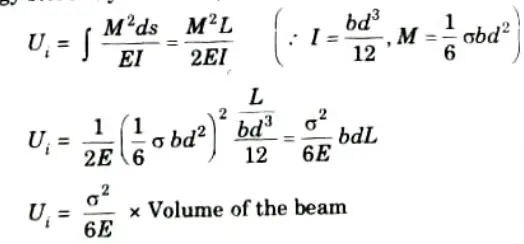
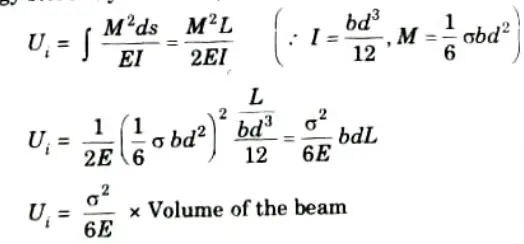
Q5. Write the equation in term of strain energy, which is sufficient to determine the stress in case of propped cantilever beams.
Ans.
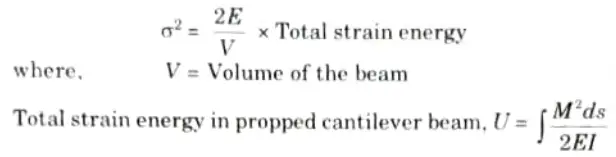
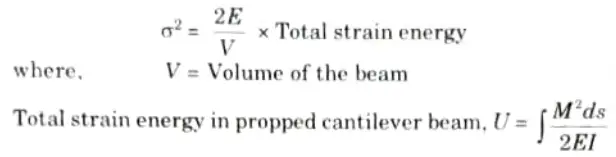
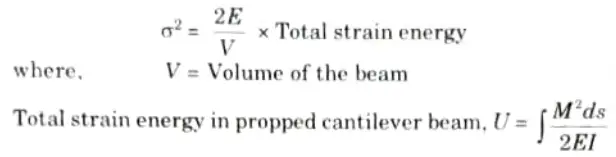
Q6. Write the statement of Maxwell’s reciprocal theorem.
Ans. In any beam or truss, whose material is elastic and obeys Hooke’s aw and whose supports remain unyielding and the temperature remain unchanged, then the deflection at any point D (i.e..𝝙D ) due to a load W acting at any other point C is equal to the deflection at any point C(i.e.,𝜹C)due to the load W acting at the point D.



Q7. Write the statement of Castigliano’s first theorem.
Ans. “The partial derivative of the total strain energy in a structure with respect to displacement at every load point yields the value of the corresponding load operating on the body in the displacement direction.”
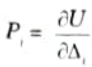
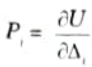
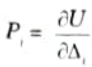
Q8. Write the statement of Castigliano’s second theorem.
Ans. The partial derivative of the strain energy with respect to load or moment at a location in any linear elastic structure is equal to the deflection or slope of the point where the load is acting. The deflection is measured in the load direction.
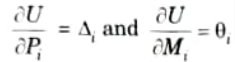
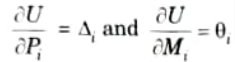
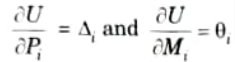
Q9. Define real work method.
Ans. When work done by actual loads is considered, the strain energy approach is also known as the real work method. From the law of conservation of energy, we can say,
Strain energy, U= Real work done by loads =
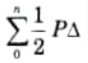
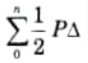
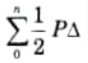
Q10. What do you understand by conjugate beam ?
Ans. Conjugate beam is an imaginary beam for which the load diagram is represented by M/EI diagram.
Q11. Give the difference between simple (or real) beam and conjugate beam.
Ans.
| S. No. | Simple (Real Beam) | Conjugate Beam |
| i. | Actual loading diagram is the loading diagram. | Bending moment diagram is the loading diagram. |
| ii. | Bending moment diagram from loading diagram provides the bending moment at any section. | Bending moment diagram from loading diagram provides the deflection at any section. |
| iii. | Shear force diagram provides the shear stress at a section. | Shear force diagram provides the slope at a section. |
Q12. State the salient features of conjugate beam method.
Ans. Following are the features of conjugate beam method:
- i. The slope at any point on the provided beam equals the shear force at the same point on the conjugate beam.
- ii. The deflection at any point on the provided beam is equal to the bending moment at the corresponding point on the conjugate beam.
Q13. What is the advantage of conjugate beam method over other method ?
Ans. Following are the advantages of conjugate beam method:
- i. This method is applying to the beams having different moment of inertia.
- ii. This method is simple, easy and consume less time.
- iii. This method is useful for calculating deflection in different loading condition.
Q14. Write down the formula of deflection and slope for simply supported beam with concentrated load W at the midspan.
Ans.



Q15. Write down the formula of deflection and slope for simply supported beam having uniformly distributed load on the Span L.
Ans.



Q16. A cantilever beam of length L subjected to a concentrated load P at the free end. What is the deflection at the free end?
Ans.



Q17. Write the formulae for area and the centroid of the curve defined by y = kxn.
Ans.



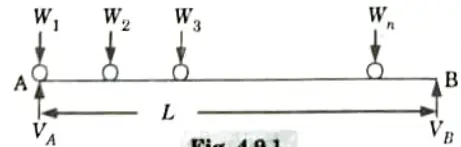
Unit-IV: Rolling Loads and Influence Line Diagrams (Short Question)
Q1. What do you understand by the term rolling load ?
Ans. Rolling Load (or Moving Load): In actual life, we frequently meet changing loads or situations that are subject to change.
Example: Axle loads of moving trucks or vehicles, wheel loads of a railway train or wheel loads of a gantry assembly on a gantry girder etc.
Q2. What do you understand by influence line ?
Ans. An influence line represents the variation of a member’s response, shear, moment, or deflection at a single spot as a concentrated load or forces that move over the member.
Q3. What are the advantages of influence lines ?
Ans. Following are the advantages of influence lines:
- i. When a structure is subjected to a live or moving load, the fluctuation in shear and bending moments in the member is best characterised using the influence line.
- ii. Using the ordinates of the influence line diagram, the amount of the related reaction, shear, and moment of deflection at the location can be computed.
- iii. Influence lines are used in the construction of bridges, industrial crane rails, conveyors, and other structures that move weights across their span.
Q4. Define influence line diagram (ILD).
Ans. An effect line diagram for the function depicted is a curve or graph that depicts the function such as a reaction at support, shear force at a section, bending moment at a section of a structure, at criteria, at various places of a unit load on the span of the structure.
Q5. What is the difference between ILD and shear force or bending moment diagrams ?
Ans. i. The ordinate of a bending moment or shear force curve gives the bending moment or shear force value at the section where the ordinate is drawn. In the case of an influence line diagram, the ordinate at any point gives the value of the bending moment or shear force only at the given Section, not at the point where the ordinate is drawn.
ii. An influence line diagram depicts the effect of a moving load only at one point on a member, whereas a shear force or bending moment diagram depicts the effect of fixed loads at all locations along the member’s axis.
Q6. State Muller-Breslau’s principle for determinate structure.
Ans. According to this principle “the influence line for a function (reaction, shear, or moment) is at the same scale as the deflected shape of the beam when the beam is acted upon by the function”.
Q7. What do you understand by influence line for beam ?
Ans. If an influence line for a function (reaction, shear, or moment) has been developed, the live loads on the beam can be positioned to produce the maximum value of function. There are two types of loadings to be considered:
- i. For concentrated load, and
- ii. For uniform load.
Q8. What do you understand by influence line for truss ?
Ans. As the truss members are solely impacted by joint loading, we can load each joint with a unit load to determine the ordinate values of the influence line for a member, then apply the technique of joints or method of selection to determine the force in the member. The information can be displayed as a table listing unit load at the joint versus force in the member.
Q9. Write the condition for maximum end shear of moving loads.
Ans.


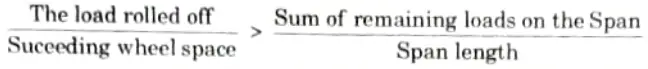
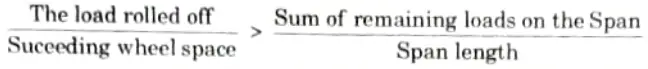
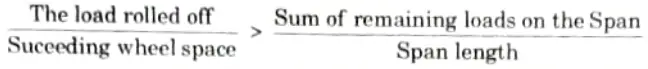
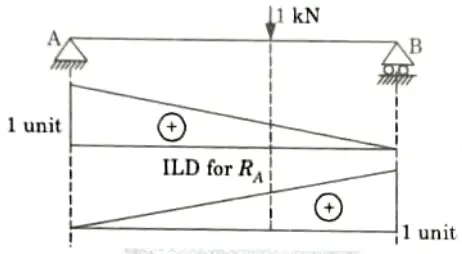
Q10. Draw the ILD of the reactions for simply supported beam.
Ans.


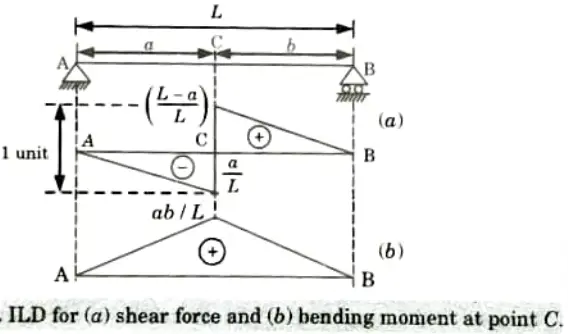
Q11. Draw the ILD of shear force and bending moment for simply supported beam at any section.
Ans.


Q12. What are the uses of influence lines?
Ans. Following are the uses of influence lines:
- i. Influence lines are used to depict how shear force and bending moment vary within a part that is being loaded or moved.
- ii. Influence lines provide guidance on where to place a moving load on a structure to maximise its influence at a given moment.
- iii. The related reaction, shear, moment, or deflection at the site can be determined using the ordinates of influence line diagram.
- iv. The structures on which the loads move over the span are designed using influence lines. The design of bridges, industrial crane rails, and conveyors, among other types of structures, are prevalent.
Q13. What are the applications of Müller-Breslau’s principle ?
Ans. Following are the applications of Müller-Breslau’s principle:
- i. The Muller-Breslau concept offers a rapid approach for determining the influence line’s form.
- ii. The ordinates at the peak can be computed using the basic technique after the geometry of the influence line is known.
- iii. By locating the live load on the beam using the geometry of the influence line, it is able to use statistics to ascertain the maximum value of the function (shear or moment).
Unit-V: Analysis of Arches (Short Question)
Q1. What do you understand by the term ‘arch’?
Ans. i. Since an arch serves as an inverted cable, it receives most of its load in compression.
ii. Since arches are rigid, depending on how they are loaded and shaped, they must also be able to resist some bending and shear.
In long span buildings, these are utilised to lessen the bending moments.
Q2. What are the different types of arches ?
Ans. Some common types of arches are given below:
i. Funicular arch, ii. Fixed arch,
iii. Two hinged arch, iv. Three hinged arch, and
v. Tied Arch.
Q3. State Eddy’s theorem as applicable to arches.
Ans. The vertical intercept between the linear arch and the actual arch’s centre line determines the bending moment at any point along the arch.
Q4. Define span of arch.
Ans. The span of the arch is the horizontal distance between the lower hinge supports. The hinges might or might not be level.
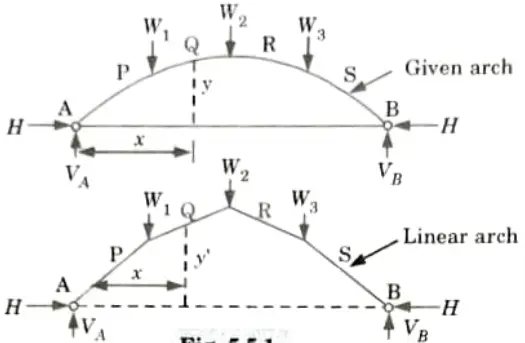
Q5. What is linear arch ?
Ans. The load exerted on the arch is supported by the arch without the development of any bending moment anywhere if the arch is formed in the shape of the funicular polygon and the points are pin linked. A linear arch is one such arch.


Q6. Define rise of arch.
Ans. The height of the crown (the highest point of the arch) above the level of the lower hinges is referred to as the rise of the arch when the arch’s supports are all at the same height.
Q7. Define horizontal thrust.
Ans. Horizontal thrust at the support refers to the horizontal component of the response at either lower end. It is denoted by H.
Q8. What do you understand by three hinged arch ?
Ans. A three hinged arch has a hinge at each abutment or springing and also at the crown. lt is statically determinate structure.
Q9. What are the different types of three hinged arch ?
Ans. Following are the types of three hinged arch :
- i. Three hinged parabolic arch, and
- ii Three hinged circular arch.
Q10. Write the equation of vertical rise in parabolic arch.
Ans. The equation of vertical rise in parabolic arch is given by,
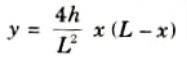
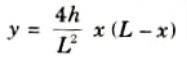
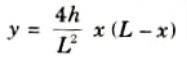
Q11. Give the equation for a parabolic arch whose springing is at different levels.
Ans. The equation is given by,



Q12. Why arches are preferred than beams?
Ans. Arches preferred than beams because:
- i. The end restraints’ inward horizontal reactions cause the arch to hog, which effectively counteracts the static sagging moments created by the vertical loads.
- ii. The resulting decrease in net moments, which contributes to an arch’s much superior load bearing capability when compared to an equivalent beam.
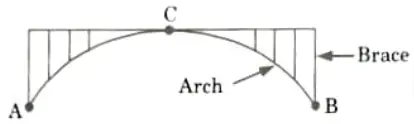
Q13. What do you mean by spandrel braced arch ?
Ans. In three hinged spandrel braced arch, the space above the arch rib and below the level of crown is known as spandrel of arch.


Q14. Draw a diagram for maximum positive bending moment due to movement of a single concentrated load of W kN in three hinged arch.
Ans.
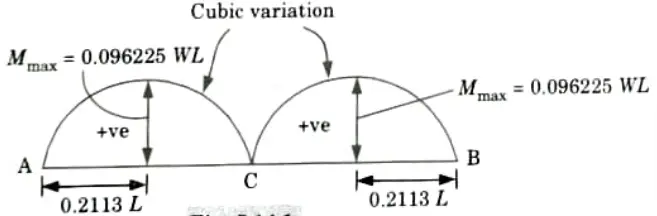


Q15. What are the different types of spandrel braced arch?
Ans. The spandrel braced arch can be of following types:
- i. Close Spandrel Arch: The area above the arch rib and below the level of the crown can be filled in closed spandrel arches.
- ii. Open Spandrel Arch: In an open spandrel arch, a truss-like system can be used to fill the space above the arch rib and below the level of the crown.
Q16. Draw the diagram for maximum negative bending moment due to movement of single concentrated load of W kN in three hinged arch.
Ans.
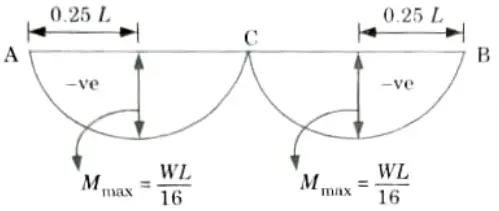


Q17. Draw the diagram for the maximum positive bending moment and maximum negative bending moment due to movement of UDL of w kN/m in three hinged arch.
Ans.
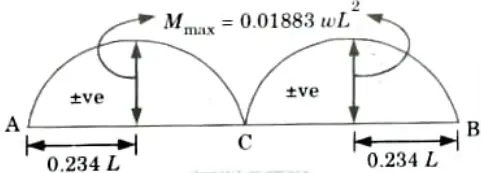


Q18. Write the effect of temperature rise on the horizontal thrust for a three hinged arch carrying a load.
Ans. Although temperature changes alone do not cause stresses to form in a three-hinged arch, it should be noted that when the rise of the arch is altered as a result of temperature change, the horizontal thrust for the arch that is already bearing a load will also vary.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Structural Analysis Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Structural Analysis Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
