B.Tech AKTU Quantum Book delves into the world of Machine Learning Techniques. Access critical notes, frequently asked questions, and essential insights for understanding this transformational field. Unit-2 Regression and Bayesian Learning
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Machine Learning Techniques: *Quantum *B.tech-Syllabus *Circulars *B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. Describe briefly linear regression.
Ans. 1. A supervised machine learning approach called linear regression produces continuous outputs with constant slopes.
2. Rather than attempting to categorise values into groups, it is used to forecast values within a continuous range (for instance, sales or price) (for example: cat, dog).
3. Following are the types of linear regression:
a. Simple regression :
i. Simple linear regression uses traditional slope-intercept form to produce accurate prediction,
y = mx + b
where, m and b are the variables,
x represents our input data and y represents our prediction.
b. Multivariable regression:
i. A multi-variable linear equation is given below, where w represents the coefficients, or weights:
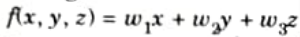
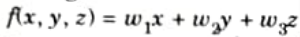
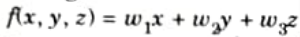
ii.The variables x, y, z represent the attributes, or distinct pieces of information that, we have about each observation.
iii. For sales predictions, these attributes might include a company’s advertising spend on radio, TV, and newspapers.
Sales = w1 Radio + w2 TV + w3 Newspapers
Q2. Differentiate between linear regression and logistics regression.
Ans.
| S. No. | Linear regression | Logistics regression |
| 1. | A supervised regression model is linear regression. | A model of supervised classification is logistic regression. |
| 2. | In Linear regression, we predict the value by an integer number. | In Logistic regression, we predict the value by 1 or 0. |
| 3. | No activation function is used. | A logistic regression equation is created by converting a linear regression equation using an activation function. |
| 4. | A threshold value is added. | No threshold value is needed. |
| 5. | It is based on the least square estimation. | The dependent variable consists of only two categories. |
| 6. | In the event that the independent variables change, linear regression is employed to estimate the dependent variable. | Logistic regression is used to calculate the probability of an event. |
| 7. | Linear regression assumes the normal or gaussian distribution of the dependent variable. | Logistic regression assumes the binomial distribution of the dependent variable. |
Q3. What are the parameters used in support vector classifier ?
Ans. Parameters used in support vector classifier are:
- 1. Kernel:
- a. The type of data and the type of transformation are taken into consideration while choosing the kernel.
- b. The kernel is a Radial Basis Function Kernel by default (RBF).
- 2 Gamma:
- a. The influence of a single training sample during transformation is determined by this parameter, which in turn determines how closely the decision borders end up enclosing points in the input space.
- b. Points further apart are regarded as similar if gamma has a modest value.
- c. As a result, more points are grouped together and the decision boundaries are smoother (may be less accurate).
- d. Greater gamma values result in points being closer together (may cause overfitting).
- 3. The ‘C’ parameter:
- a. This parameter regulates the degree of regularization that is done to the data.
- b. Low regularization, indicated by large values of C, results in excellent fit of the training data (may cause overfitting).
- c. More regularization, which results in a lower value of C, makes the model more error-tolerant (may lead to lower accuracy).
Q4. Explain Bayesian network by taking an example. How is the Bayesian network powerful representation for uncertainty knowledge ?
Ans.
- 1. A Bayesian network is a directed acyclic graph in which each node is annotated with quantitative probability information.
- 2. The full specification is as follows:
- i. A set of random variables makes up the nodes of the network variables may be discrete or continuous.
- ii. A set of directed links or arrows connects pairs of nodes. If there is an arrow from x to node y, x is said to be a parent of y.
- iii. Each node xi has a conditional probability distribution P(xi |parent (xi)) that quantifies the effect of parents on the node.
- iv. The graph has no directed cycles (and hence is a directed acyclic graph or DAG).
- 3. A Bayesian network offers an exhaustive account of the domain. The data in the network can be used to determine each entry in the whole joint probability distribution.
- 4. Bayesian networks give the field a clear approach to depict conditional independence relationships.
- 5. An exponentially smaller Bayesian network frequently exists than the total joint distribution.
For example:
- 1. Suppose we want to determine the possibility of grass getting wet or dry due to the occurrence of different seasons.
- 2. The weather has three states : Sunny, Cloudy, and Rainy. There are two possibilities for the grass: Wet or Dry.
- 3. The sprinkler can be on or off. Ifit is rainy, the grass gets wet but if it is sunny, we can make grass wet by pouring water from a sprinkler.
- 4. Suppose that the grass is wet. This could be contributed by one of the two reasons – Firstly, it is raining. Secondly, the sprinklers are turned on.
- 5. Using the Baye’s rule, we can deduce the most contributing factor towards the wet grass.
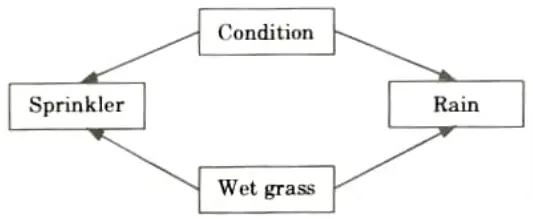


Bayesian network possesses the following merits in uncertainty knowledge representation:
- 1. The Bayesian network can easily accommodate missing data.
- 2. A Bayesian network can pick up on a variable’s haphazard relationship. In data analysis, a casual relationship is beneficial for comprehending field knowledge and can readily result in precise prediction even in the presence of significant interference.
- 3. Field knowledge and data-based information can be fully utilised when a bayesian network and bayesian statistics are combined.
- 4. Combining the Bayesian network with different models can successfully prevent the over-fitting issue.
Q5. Describe the usage, advantages and disadvantages of EM algorithm.
Ans. Usage of EM algorithm:
- 1. It can be used to complete the gaps in a sample’s data.
- 2. It can serve as the foundation for cluster learning that is unsupervised.
- 3. It can be utilised to estimate the Hidden Markov Model’s parameters (HMM).
- 4. lt can be used to determine latent variable values.
Advantages of EM algorithm are:
- 1. With each iteration, the likelihood is always certain to rise.
- 2. In terms of implementation, the E-step and M-step are frequently quite simple for many issues.
- 3. The closed form of solutions to the M-steps is frequently seen.
Disadvantages of EM algorithm are:
- 1. It has slow convergence.
- 2. It makes convergence to the local optima only.
- 3. It needs both the forward and backward probabilities (numerical optimization requires only forward probability).
Q6. What are the advantages and disadvantages of SVM ?
Ans. Advantages of SVM are:
- 1. Guaranteed optimality: Owing to the nature of Convex Optimization, the solution will always be global minimum, not a local minimum.
- 2. The abundance of implementations: We can access it conveniently.
- 3. Both linearly and non-linearly separable data can be used with SVM. Whereas non-linearly separable data presents a soft margin, linearly separable data crosses the hard margin.
- 4. SVMs offer semi-supervised learning models conformance. It can be applied to both labelled and unlabeled data sets. The transductive SVM is just one of the conditions needed to solve the minimization problem.
- 5. Feature mapping used to place a significant burden on the computational complexity of the model’s overall training efficiency. But, SVM may perform the feature mapping using the straightforward dot product with the aid of Kernel Trick.
Disadvantages of SVM:
- 1. As compared to other text data handling techniques, SVM does not provide the best performance when handling text structures. This causes a loss of sequential information, which affects performance.
- 2. Unlike logistic regression, SVM cannot provide the probabilistic confidence value. Due to the importance of prediction certainty in many applications, this doesn’t really explain anything.
- 3. The support vector machine’s major drawback may be the kernel selection. It becomes challenging to select the best kernel for the data because there are so many of them available.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Machine Learning Techniques Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Machine Learning Techniques Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
