The most important or commonly asked question in Bachelor of engineering / AKTU for network analysis and synthesis Unit 2 Network Theorems. I hope this session helps you prepare for your future examinations.
Que 1. Explain why the “superposition theorem” is not applicable for power verifications of a given network ? Explain the following:
i. Linearity principle.
ii. Homogeneity principle.
Power, P = I2R, is a non-linear variable, hence the superposition theory cannot be used. Superposition theorems can only be applied to linear variables like voltage and current.
B. Linearity principle:



Que 2. State reciprocity theorem in AC network.
1. Regarding an exchange between the places of application of input and measurement of output, the ratio of input to output in a reciprocal network remains constant for a linear, time-invariant, bilateral network.
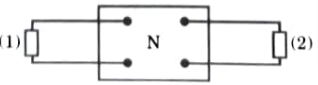


2.Consider a reciprocal network N, as shown in Fig. 2.7.1. Now, apply a voltage source of emfE, in branch I2 which produces current I2 in branch 2 as shown in Fig. 2.7.2.
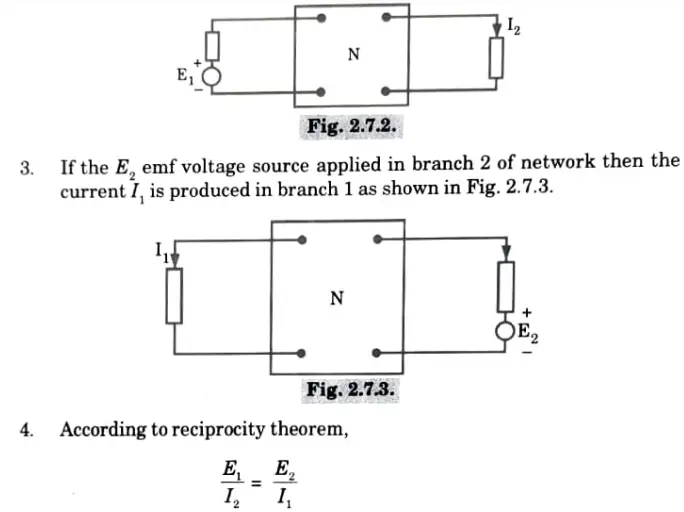


Que 3. State and prove the maximum power transfer theorem applied to the AC circuits.
|OR|
State and prove maximum power transfer theorem with example.
Ans.
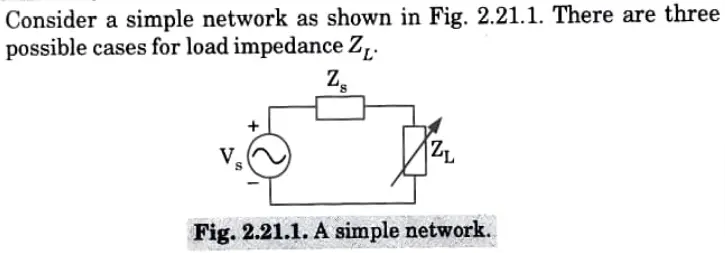


Case I: When the load impedance is a variable resistance.



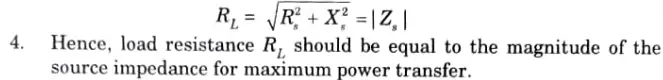
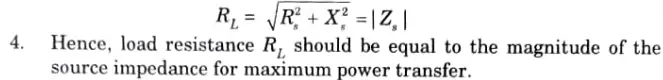
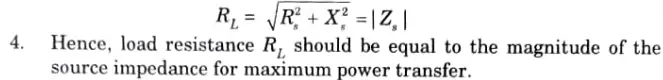
Case II: When the load impedance is a complex impedance with variable resistance and variable reactance.



Case III: When the load impedance is a complex impedance with variable resistance and fixed reactance.






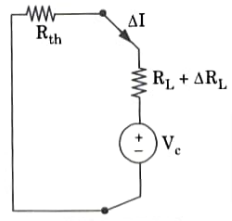
Que 4. Give the statement of compensation theorem. Also prove it for linear networks.
Statement: In a linear time variant network, when the resistance (R) of an uncoupled branch, carrying a current (, is changed by (𝚫R), the current in all the branches would change and can be obtained by assuming that an ideal voltage source (VC) has been connected in series with R+ 𝚫R), when all other sources in the network are replaced by their internal resistance.
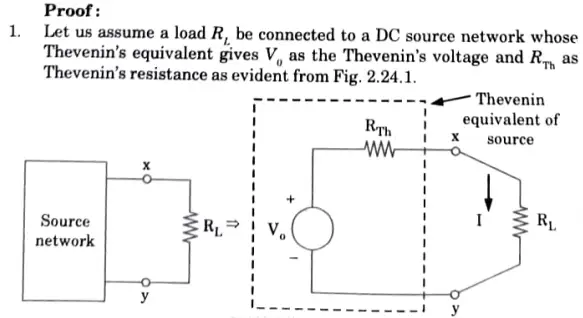


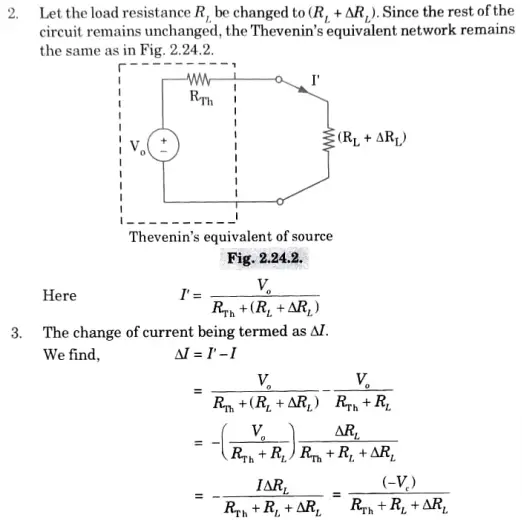


4. Thus it has been proved that change of branch resistance, branch current is changed and the change is equivalent to an ideal compensating voltage source in series with the branch opposing the original current.


Que 5. State and prove Tellegen’s theorem.
Ans.








Que 6. State and explain “compensation theorem” and
“Tellegen’s theorem” in circuit theory. Also mention their significance and limitations. What are the advantages and disadvantages of “Tellegen’s and reciprocity theorems”.
ANSWER Compensation theorem: Statement: In a linear time variant network, when the resistance (R) of an uncoupled branch, carrying a current (, is changed by (𝚫R), the current in all the branches would change and can be obtained by assuming that an ideal voltage source (VC) has been connected in series with R+ 𝚫R), when all other sources in the network are replaced by their internal resistance.
Significance of compensation theorem :
The incremental changes in voltage and current in circuit branches caused by a change in impedance in one branch are calculated using this theorem.
Limitations of compensation theorem:
1. This theorem is not applicable to circuits with only dependent sources.
2. This theorem is not applicable to circuits with non-linear elements.
Tellegen’s theorem:



Significance of Tellegen’s theorem:
According to this theorem, the total amount of power absorbed (or dissipated or stored) by all other network elements must equal the power given by independent sources of the network.
Limitations of Tellegen’s theorem:
The only limitation is that the voltages Vr satisfy KVL and the currents Ir satisfy KCL.
Advantages of reciprocity theorem:
The networks made up of linear, time-invariant, bilateral passive components like common resistors, inducers, capacitors, and transformers are suitable to this theorem.
Disadvantages of reciprocity theorem :
- Unilateral networks, such as those made up of electron tube networks or other control devices, are not covered by this theorem.
- Circuits having constituents that change in time are not covered by this theorem.
- This theorem is inapplicable to circuits with dependent sources.
Advantages of Tellegen’s theorem:
- Any lumped network with members that are linear or nonlinear, active or passive, time variable or time invariant, can use this theorem.
- This theorem only addresses the network’s graph and is wholly unrelated to the characteristics of its constituent elements.
Disadvantages of Tellegen’s theorem:
1. This theorem is not concerned with the type of circuit elements.
2. This theorem is only based on the two Kirchhoff’s laws.



Syllabus | Quantums | notes | Important Questions
Network Analysis and Synthesis Important Links:
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Network Analysis and Synthesis Quantum PDF: | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |

2 thoughts on “Unit2 Network Theorems | network analysis and synthesis notes”