With the B.Tech AKTU Quantum Book, you may delve into the world of Heat and Mass Transfer. Find important notes, repeated questions, and essential insights to succeed in this subject. Unit-2 Fins and Transient Conduction
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Heat and Mass Transfer: *Quantum *B.tech-Syllabus *Circulars *B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. What do you understand by fins and also explain types of fins?
Ans. A. Fins:
- 1. When the available surface is deemed insufficient to transfer the necessary amount of heat with the available temperature drop and convective heat transfer coefficient, these expanded surfaces are employed to increase the rate of heat transfer from the surfaces.
- 2. Conduction and convection between a surface’s boundary and its surroundings are responsible for heat transmission through fins.
B. Types of Fins : Fins are of two types:
- 1. Fins of uniform cross-sectional area :
- a. Fins of rectangular profile, and
- b. Fins of circular profile.
- 2. Fins of non-uniform cross-sectional area :
- a. Longitudinal fin of trapezoidal profile,
- b. Longitudinal fin of parabolic profile, and
- c. Truncated conical spline.
Q2. What is the reason for the widespread use of fins on surfaces?
Ans.
- 1. In order to boost the rate of heat transfer from an existing surface, fins are typically employed to add extra surface area.
- 2. In the majority of real-world scenarios, liquid and gas are used as heat transfer fluids.
- 3. When there is a heat transfer between a liquid and a gas, the gas provides more heat transfer resistance since it has a lower heat transfer coefficient.
- 4. As a result, more surface area is offered by utilizing fins to speed up heat transfer on the petrol side.
- 5. Surfaces with fins are used in air-cooled cylinders and refrigerator condenser tubes.
Q3. Explain transient heat conduction.
Ans.
- 1. The term transient or unsteady state designates a phenomenon which is time dependent.
- 2. Heat flow and temperature distribution at every point in the system are continuously changing over time under conditions known as unsteady state heat conduction.
- 3. Transient conditions occur in :
- i. Cooling of IC engine,
- ii. Automobile engines,
- iii. Heating and cooling of metal billets,
- iv. Heat treatment of metals by quenching, and
- v. Brick burning.
- 4. The temperature field in any transient problem is given by,
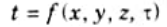
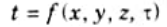
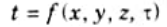
- 5. The two types of variation in temperature during an unsteady state are as follows:
a. Non-Periodic Variation:
- 1. The temperature at every location inside the system varies nonlinearly with time in a nonperiodic transient state.
- 2. Examples:
- i. Heating of an ingot in a furnace, and
- ii. Cooling of bars, blanks and metal billets in steel works, etc.
b. Periodic Variation:
- 1. In a periodic transitory condition, temperatures change on a regular or irregular, but unmistakably cyclic, basis.
- 2. Any function that is cyclic but not necessarily harmonic characterises an irregular periodic variation, whereas a regular periodic variation is characterised by a harmonic sinusoidal or non-sinusoidal function.
- 3. Examples: The temperature variations in:
- i. Cylinder of an IC engine,
- ii. Building during a period of 24 hours, and
- iii. Surface of earth during a period of 24 hours.
Q4. Consider heat transfer between two identical hot solid bodies and the air surrounding them. The first solid is being cooled by a fan while the second one is allowed to cool naturally. For which solid is the lumped system analysis more likely to be applicable ? Why?
Ans. 1. Lumped system analysis is applicable to the system when the Biot number is less than 0.1.



2.Now that both systems in the current situation share the same material and geometry, the Biot number solely depends on the value of the heat transfer coefficient.
3. Since the solid body in the first case is cooled by blowing air with a fan, the value of ‘h’ will be higher than in the second situation, when the solid body is cooled naturally.
4. Since the Biot number is higher in the first case than the second case, the solid that is being cooled by natural convection as opposed to forced convection will more likely be subject to the lumped system analysis.
Q5. Explain the utility of Heisler chart in transient heat conduction problem.
Ans. A. Heisler Charts:
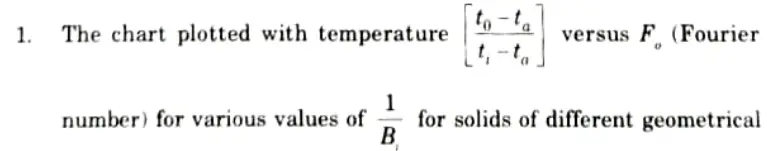
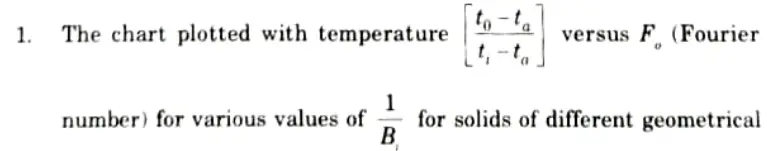
shapes such as plates, cylinders and spheres are known as Heisler charts.
2. The temperatures at other locations are calculated by multiplying the mid plane temperature by the correction factor taken from the charts. These charts show the temperature history of the solid at its mid planes (x = 0).
3. From Heisler chart, the value of Bi (Biot number) and Fo (Fourier number) are calculated on the basis of characteristic parameter S which is semi-thickness in case of plates and surface radius in case of cylinder and spheres.
4. Heisler charts are extensively used to determine the temperature distribution.
B. Use of Heisler Charts to Obtain Temperature Distribution when both Conduction and Convection Resistances are almost of Equal Importance:
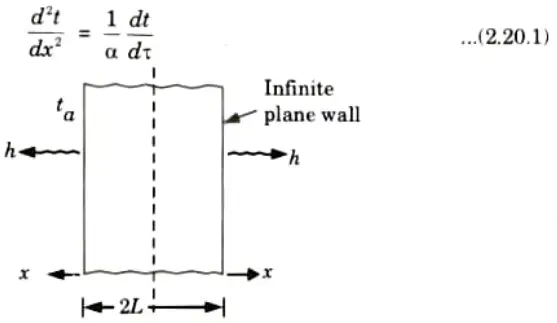
1. Consider the heating and cooling of a plane wall having a thickness of 2 and extending to infinity in y and z
2. Let directions. us assume that the wall initially is at uniform temperature ti and both surfaces (x = ± L) are suddenly exposed to and maintained at the ambient (surroundings) temperature t.
3. The governing differential equation is


4. The boundary conditions are:
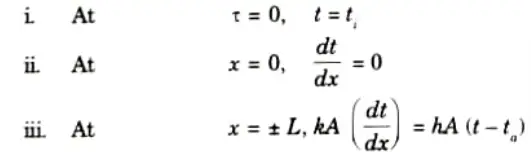
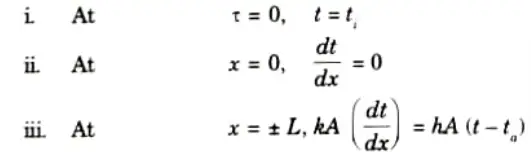
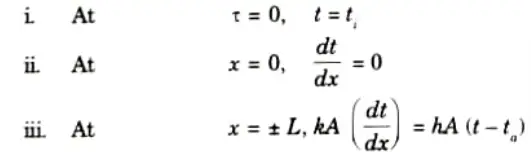
5. The solutions obtained after mathematical analysis indicate that



6. From eq. (2.20.2), it is evident that when conduction resistance is not negligible, the



Q6. A large metal plate of thickness 5 cm is initially at 460 °C. It is suddenly exposed to fluid at 100 °C with a convection coefficient of 142.5 W/m2-K. Find the time needed for its mid plane to reach a temperature of 316 °C and surface temperature at the same instant of time. Take k = 21.25 W/m-K and 𝛂 = 12 x 10-5 m2/sec.
Ans.
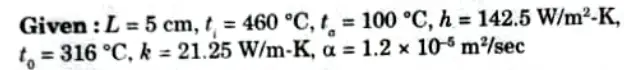
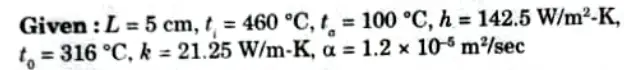
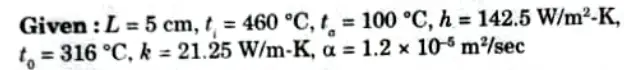
To Find: i. Time.
ii. Surface temperature.
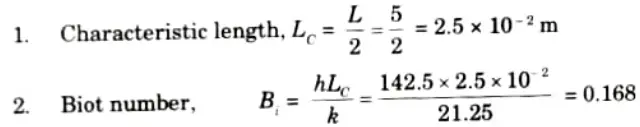
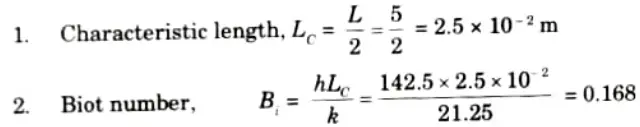
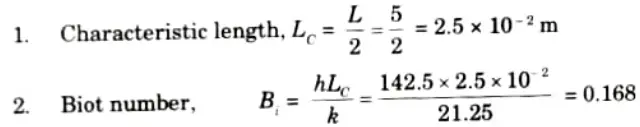
As Bi > 0.1, therefore lumped analysis cannot be applied in this case, further as Bi < 100, Heisler charts can be used to obtain the solution of the problem.
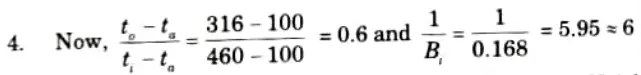
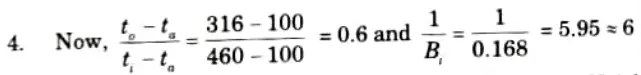
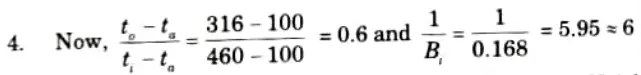
Corresponding to the above parametric values, from Heisler charts,






Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Heat and Mass Transfer Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Heat and Mass Transfer Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One View) | Student Result |
