Quantum Notes can help you learn more about Electrical Machines-II. To ace your Aktu Btech examinations, gain access to crucial, commonly asked questions. With us right now, advance! Unit-2 Synchronous Machine-II
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Electrical Machines-II: * Aktu Quantum * B.tech-Syllabus * Circulars * B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Q1. From the phasor diagram of the salient pole synchronous machine, show that:
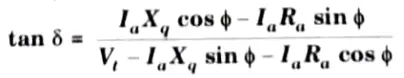
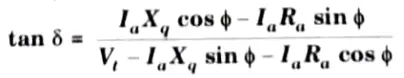
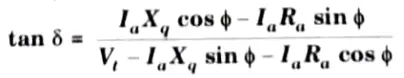
where the symbols having their usual meanings.
Ans. 1. The phasor diagram for a lagging pf salient pole synchronous motor is shown in the Fig.
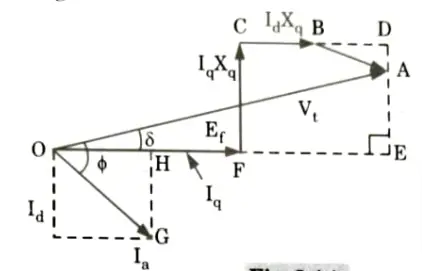


2. From phasor diagram,
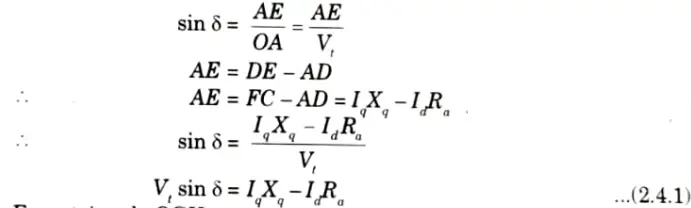
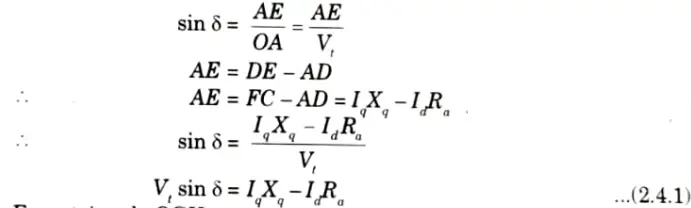
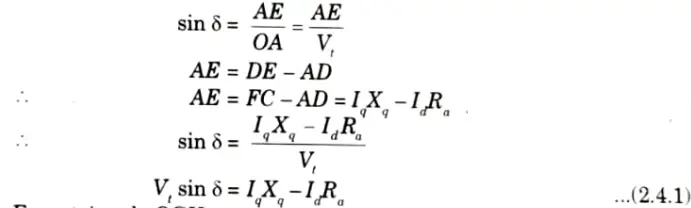
3. From triangle OGH,
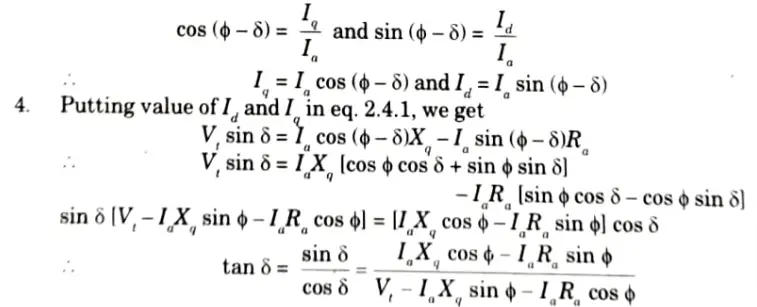
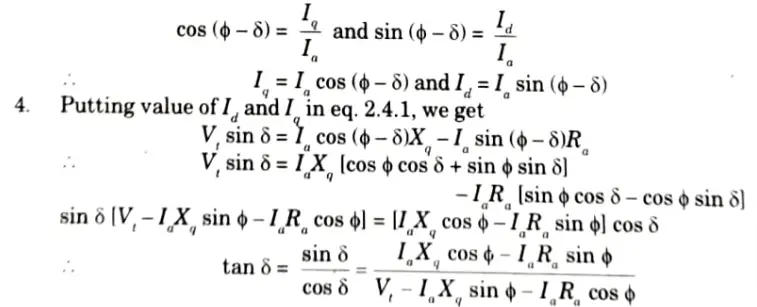
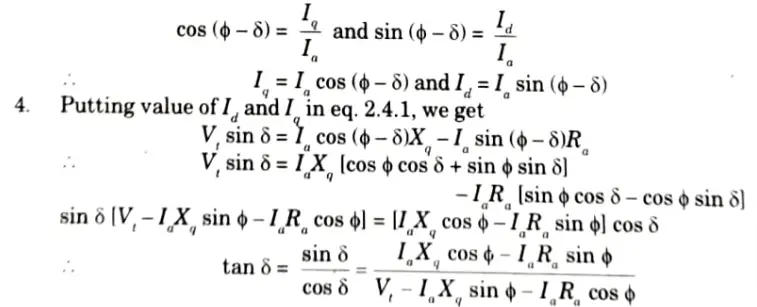
Q2. Explain the constructional features and working principle of the synchronous motor and develop the torque expression of synchronous motor.
Ans. A. Construction:
It consists of two parts:
- 1. Stator: A three-phase star or delta linked winding is used. A three-phase alternating current supply powers this.
- 2. Rotor: A rotor is a sort of field winding that can be salient (projected pole) or non-salient (cylindrical). The majority of synchronous motors have a salient, or projecting pole, structure. A separate DC supply excites the field winding through slip rings.
B. Working principle:
- 1. Consider the 2-pole synchronous motor. When a 3-phase AC voltage is applied to the stator winding, a rotating magnetic field is produced in the air gap.
- 2. The stator field rotates at synchronous speed.
- 3. The motor’s field current generates a steady-state magnetic field. As a result, the machine contains two magnetic fields.
- 4. The rotor will gravitate towards the stator field. Because the stator magnetic field is spinning, the rotor magnetic field and rotor will tend to revolve with the stator’s rotating field.
- 5. The two fields must be stationary with regard to each other in order to create a continuous torque. This is only possible if the rotor rotates at the same rate. As a result, the rotor revolves at synchronised speed.
C. Torque Expression:
1. Net input to the synchronous motor is the three-phase input to the stator.



3. Now in stator, due to its resistance Ra per phase there are stator copper where losses.
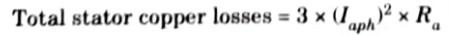
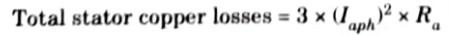
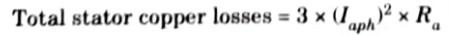
4. The remaining power is converted to the mechanical power, called gross mechanical power developed by the motor denoted as Pm.
Pm = Pin – Stator copper losses
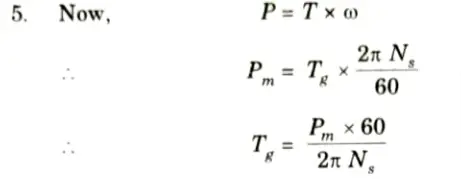
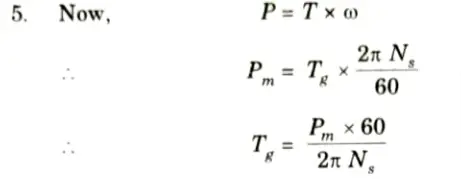
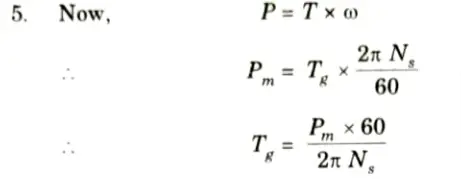
This is the gross mechanical torque developed.
6. Net output of the motor can be obtained by subtracting friction and winding i.e., mechanical losses from gross mechanical power developed.
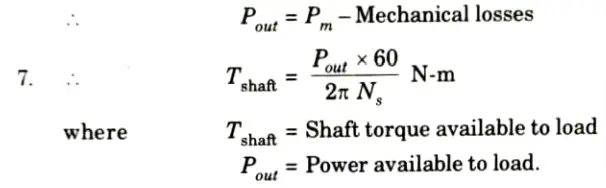
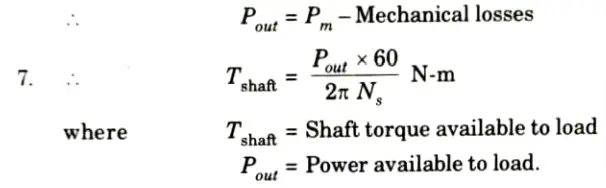
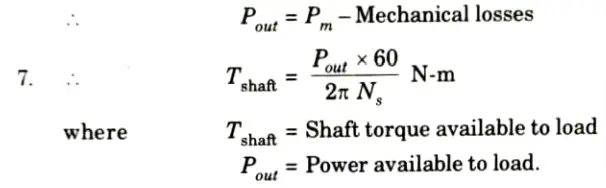
Q3. Explain why 3ɸ synchronous machines are not self starting ? What are the methods for starting of the 3ɸ synchronous machines ?
Ans. A. Reason:
- 1. Consider a 2-pole synchronous motor. When a 3-phase AC voltage is applied to the stator winding, a rotating magnetic field is produced in the air gap. The stator field rotates at synchronous speed.
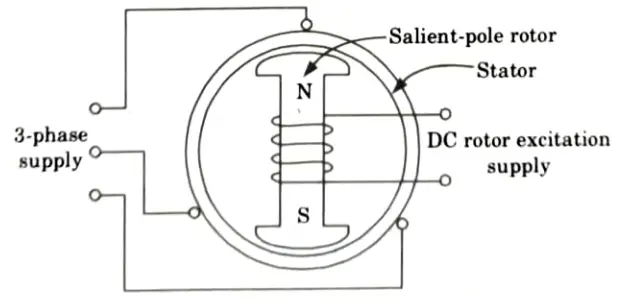


- 2. The motor’s field current generates a steady-state magnetic field.
- 3. As a result, the machine contains two magnetic fields. The rotor will gravitate towards the stator field.
- 4. Because the stator magnetic field rotates, the rotor magnetic field and rotor will tend to spin with the stator’s rotating field.
- 5. The two fields must be stationary with regard to each other in order to create a continuous torque.
- 6. This is only possible if the rotor likewise rotates at synchronous speed.
- 7. Assume the rotor is still stationary. When a synchronous pair of rotating stator poles sweeps over the stationary rotor poles, the stator poles tend to rotate the rotor in one direction and then the other.
- 8. Nevertheless, because to rotor inertia, the stator field moves so quickly that the rotor cannot keep up.
- 9. As a result, the rotor does not move, and the beginning torque is zero. As a result, a synchronous motor does not self-start.
B. Starting methods:
- i. Motor starting with an external prime mover:
- 1. An external motor drives the synchronous motor and brings it to synchronous speed in this way.
- 2. As a synchronous generator, the synchronous machine is thus synchronised with the bus-bar. The prime mover is then turned off.
- 3. Once connected in parallel, the synchronous machine will function as a motor.
- 4. Now attach the load to the synchronous motor. Because no load is applied to the synchronous motor before synchronisation, the starting motor must overcome the synchronous motor’s inertia at no load.
- 5. As a result, the starting motor’s rating is substantially lower than the synchronous motor’s rating.
- 6. At present most of large synchronous motors are provided with brushless excitation systems mounted on their shafts. These exciters are used as starting motors.
- ii. Motor starting with damper windings:
- 1. A damper winding is made up of hefty copper bars that are put into slots on the rotor’s pole faces.
- 2. End rings at both ends of the rotor short-circuit these bars. As a result, these short-circuited bars wrap together to produce a squirrel-cage winding.
- 3. When a three-phase power source is attached to the stator, the synchronous motor with damper winding begins as a three-phase induction motor.
- 4. As the motor approaches synchronous speed, the field windings are subjected to DC stimulation.
- 5. At a specific point, the motor is pulled into synchronism and begins rotating at a synchronous pace. The relative velocity between the damper winding and the revolving magnetic field is zero when the rotor revolves at synchronous speed.
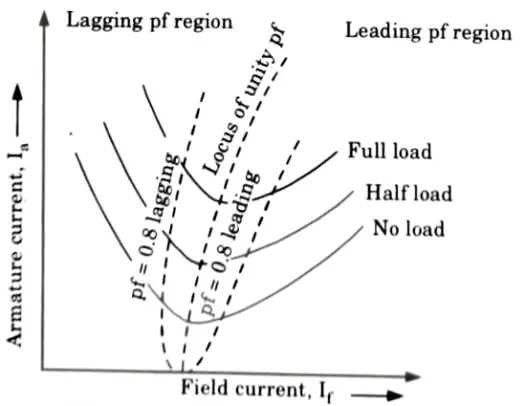
Q4. Define the V-curves and inverted V-curves at different loading conditions of synchronous motors.
Ans.
- 1. Let us assume that the motor is operating at no load.
- 2. If the field current is increased from this small value, the armature current Ia, decreases until the armature current becomes minimum and the motor is operating at unity power factor. Upto this point the motor was operating at a lagging power factor.
- 3. If the field current is increased further, the armature current increases again and the motor starts to operate at a leading power factor.
- 4. If a graph is plotted between armature current Ia and field current If at no load, the lowest curve in Fig. is obtained.
- 5. If this procedure is repeated for various increased loads, a family of curves is obtained as shown in Fig.
- 6.. Since the shape of these curves resembles the letter “V”, these curves are commonly known as V-curves of a synchronous motor.
- 7. The V-curves are useful in adjusting the field current. Increasing the field current If beyond the level for minimum armature current Ia results in leading power factor and vice-versa.


- 8. Therefore, by controlling the field current of a synchronous motor, the reactive power supplied to or consumed from the power system can be controlled.
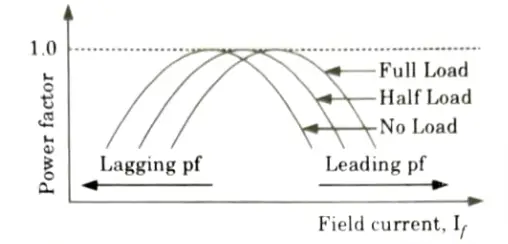
- 9. A family of curves is also obtained by plotting the power factor versus field current. These are inverted V-curves as shown in Fig.


Q5. A 5MVA, 11 kV, 50 Hz, 4 pole, star-connected synchronous generator with synchronous reactance of 0.7 p.u. is connected to an infinite bus. Find synchronising power and the corresponding torque per unit of mechanical angle displacement:
i. At no load
ii. At full load of 0.8 p.f. lagging
Ans. Given: VL = 11 kV, Xs = 0.7 p.u., P = 4
To Find: Synchronising power, Psy and
Synchronising torque, Tsy at no-load and full load of 0.8 pf












Q6. What are the applications of synchronous motor?
Ans.
- 1. Power factor correction.
- 2. Voltage regulation and
- 3. Constant speed, constant-load drives.
- 4. They are used in power plants and substations to increase power factor by running parallel to the busbars.
- 5. They are used to improve the power factor of power apparatus that operate at lagging power.
- 6. These motors are also used to adjust voltage at transmission line ends.
- 7. Because of the better efficiency of synchronous motors, they can be used advantageously for loads requiring consistent speed.



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Electrical Machines-II Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Electrical Machines-II Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |
