Learn about Digital Signal Processing B.Tech AKTU Quantum Book Short Question Notes. To process and improve digital signals, unleash the concepts of signal analysis, filtering, and transformation.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Digital Signal Processing: *Quantum *B.tech-Syllabus *Circulars *B.tech AKTU RESULT * Btech 3rd Year * Aktu Solved Question Paper
Unit-I: Introduction to Digital Signal Processing (Short Question)
Q1. Define digital signal processing.
Ans. Digital signal processing is a technique for obtaining information from digital signals using a digital processor. The output signals are also digital.
Q2. Draw the block diagram of digital signal processing.
Ans.



Q3. Explain the basic elements required for realization of digital system.
Ans. 1. Analog to digital converter.
2. Digital signal processor
3. Digital to analog converter.
Q4. What are the advantages for representing the digital system in block diagram form?
Ans.
- i. The computation algorithm can be easily written just by looking at it.
- ii. The hardware requirements are easily ascertainable.
- iii. The transfer function can simply be used to generate a number of equivalent block diagram representations.
- iv. It is possible to discover the relationship between the output and the input.
Q5. List any five applications of DSP.
Ans.
- i. Telecommunication.
- ii. Military.
- iii. Consumer electronics.
- iv.Image processing
- v. Speech processing
Q6. Enumerate the advantages of DSP over ASSP.
Ans.
- 1. DSP is more flexible than ASP.
- 2. Accuracy of DSP is greater than ASP.
- 3. DSP has better storage capability over ASP.
- 4. DSP has mathematical processing function that is not present in ASP.
Q7. Define the canonic and non-canonic structures.
Ans. A. Canonic structure: The realization structure is characterized as canonic if the number of delays in the basic realization block diagram equals the order of the difference equation or the order of the transfer function of a digital filter.
B. Non-canonic structure: If the number of delays in the structure is not the same as the order, it is referred to as a non-canonic realisation or structure.
Q8. How an IIR filter is different than FIR filter?
OR
What is difference between IIR and FIR filter ?
Ans.
| S. No. | FIR filter | IIR filter |
| 1. | They have finite impulse response. | They have infinite impulse response. |
| 2. | Always stable. | Sometimes unstable. |
| 3. | Have exact linear phase response. | Non-linear phase response. |
| 4. | It requires more memory, higher computational complexity and involves more parameters. | It uses less memory, has a lower computational complexity, and has fewer parameters. |
Q9. What is the main disadvantage of direct form realization ?
Ans. i. They are lack hardware flexibility.
ii. The susceptibility of the coefficients to the quantization effect grows with filter order due to finite precision arithmetic.
Q10. How can we obtain parallel realization of IIR system ? Also where it is used ?
Ans. The transfer function of an IIR system can be realized in parallel using the partial fraction expansion.
The parallel realization is useful for high speed filtering applications.
Q11. What are the advantages of ladder structures?
Ans. i. The ladder type of realization has good coefficient sensitivity features.
ii. They require minimum amount of memory.
Q12. Why parallel realization is used for high speed filtering applications ?
Ans. Because the filter operation is performed in parallel, the processing is done concurrently.
Q13. What is the fundamental time period of the signal x(t) = sin 15 𝛑t.
Ans. Given: x(t) = sin 15 𝛑t
To Find: T.
1. 𝛚 = 15𝛑
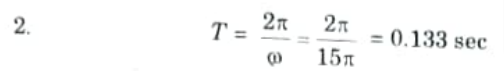
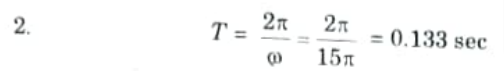
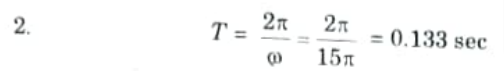
Q14. For the given system function,
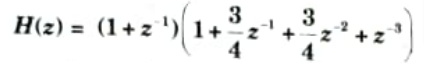
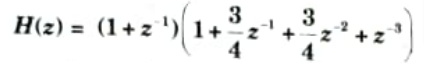
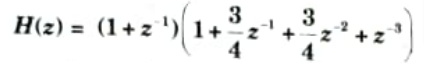
Obtain cascade realization with minimum number of multipliers.
Ans.
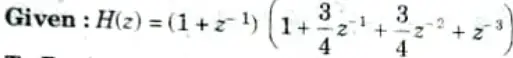
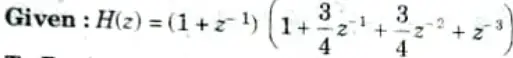
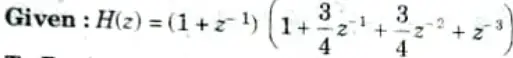
To Design: Cascade form realization. For cascade realization


Unit-II: IIR Digital Filter Design (Short Question)
Q1. Define filter.
Ans. A filter is one that rejects undesired frequencies from an input signal while allowing the desired frequencies to pass through.
Q2. Name the methods or techniques used in designing of IIR filters.
Ans. i. Approximation of derivatives.
ii. Impulse invariant method.
iii. Bilinear transformation.
Q3. What are the main disadvantages of designing IIR filters using windowing technique?
Ans. i. Impulse response is infinite
ii. It is hard to optimize than FIR.
iii. It is non-stable.
Q4. What do you mean by impulse invariant method of IIR filter design ? Give its transformation formula also.
Ans. 1. The desired impulse response of the digital filter is obtained using this technique by evenly sampling the impulse response of the analogous analogue filter.
i.e., h(n) = ha (nT)
where T is the sampling interval.
2. Its transformation formula is given by,
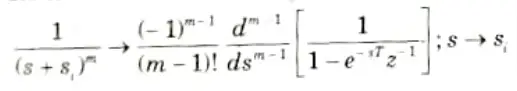
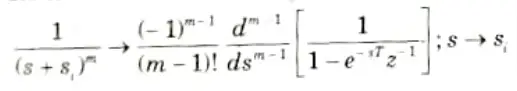
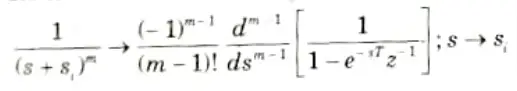
Q5. What are the limitations of impulse invariant and approximation of derivatives methods of design ?
Ans. These methods are ineffective for creating high-pass and band-reject filters.
Q6. How the limitation of impulse invariant and approximation of derivatives method is overcome ?
Ans. These approaches’ limitations can be overcome by using a mapping technique known as bilinear transformation.
Q7. What is bilinear transformation ?
Ans. 1. A bilinear transformation is a one-to-one mapping from the s-domain to the z-domain, i.e., a conformal mapping that turns the j-axis into the unit circle in the -plane only once, preventing frequency component aliasing.
2. The bilinear transformation is accomplished by numerically integrating the trapezoidal formula.
Q8. Write down the advantages and disadvantages of bilinear transformation.
Ans. Advantages of bilinear transformation method :
- i. The mapping is one to one.
- ii. There is no aliasing effect.
- iii. The steady analogue filter is converted to a stable digital filter.
- iv. There are no limitations on the types of filters that can be modified.
Disadvantages of bilinear transformation method :
1. The mapping is non-linear in this method due to the frequency warping effect.
Q9. What is the warping effect?
Ans. The mapping of frequency from 𝛀 to 𝝎 is approximately linear for small value of 𝜴 and 𝝎. For the higher frequencies, however the relation between 𝜴 and 𝝎 becomes highly non-linear. This introduces the distortion in the frequency scale of digital filter relative to analog filter. This effect is known as warping effect.
Q10. What is the equation for order of Butterworth filter?
Ans. The Butterworth low-pass filter has a magnitude response given by,
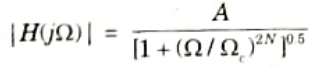
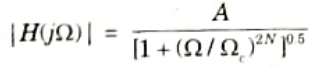
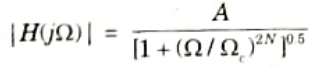
where A is the filter gain and 𝛀c is the 3 dB cut-off frequency and N is the order of the filter.
Q11. What do you mean by Chebyshev filters?
Ans. 1. The Chebyshev low-pass filters has a magnitude response given by,



Q12. Write the frequency transformation rule for the conversion of LP to HP filter.
Ans. To convert low-pass with cut-off frequency 𝛀c to high-pass with cut-off frequency 𝛀c,
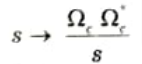
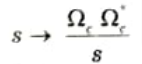
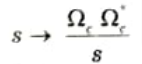
The system function of the high-pass filter is then,
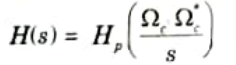
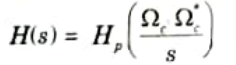
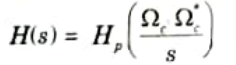
Unit-III: FIR Filter Design (Short Question)
Q1. What is window and why it is necessary ?
Ans. Window: A window function is a mathematical function that is zero-valued outside of a given interval, which is generally symmetric about the interval’s centre.
Necessity: Enhance the ability of an FFT to extract spectral data from signals.
Q2. What are advantages and disadvantages of window methods ?
Ans. Advantages of window design method:
- i. Simple method for design.
- ii. Depending on the application, different window functionalities can be employed.
Disadvantages of window design method :
- i. Lack of precise control of the critical frequencies 𝝎p and 𝝎s.
- ii. 𝝎p and 𝝎s depend upon type of window and filter length M.
Q3. What are the desirable characteristics of the window function?
Ans. i. The fourier transform of the window function W(ejw) should have small width of main lobe containing as much of the total energy as possible.
ii. The fourier transform of the window function W(ejw) should have sidelobes that decrease in energy rapidly as 𝝎 tends to 𝝅.
Q4. What are the types of window functions?
Ans.
- i. Rectangular window function.
- ii. Hanning window function.
- iii. Hamming window function.
- iv. Blackman window function.
- v. Bartlett window function.
- vi. Kaiser window function.
Q5. Write Gibbs phenomena.
Ans. The abrupt termination of the fourier series causes oscillations in the passband and stopband. These oscillations are caused by the sluggish convergence of the fourier series, particularly around the regions of discontinuity. The Gibbs phenomenon describes this result.
Q6. How can we reduce the Gibbs oscillations ?
Ans. By multiplying the required impulse response coefficients by a suitable window function, the undesired oscillations (Gibbs oscillations) can be eliminated.
Q7. What is Blackman window function ?
Ans. 1. Causal Blackman window function
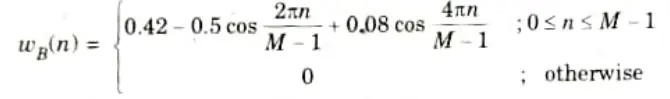
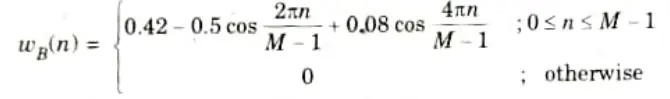
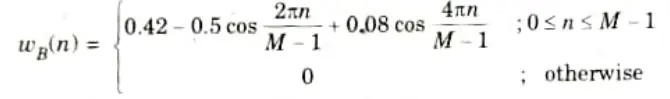
2. Non-causal Blackman window function
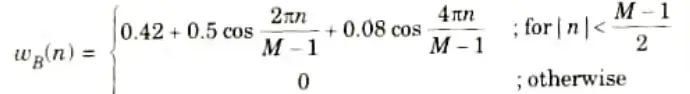
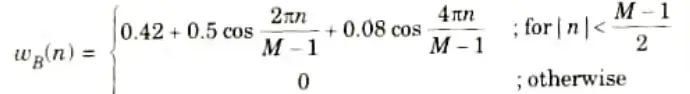
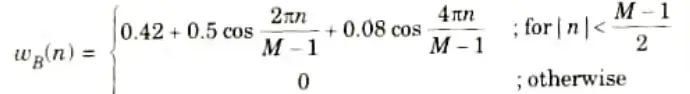
Q8. Write the expression for Hamming window.
Ans. a. Causal Hamming window:
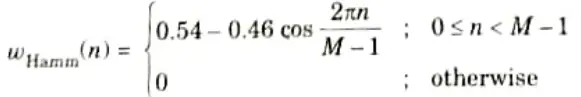
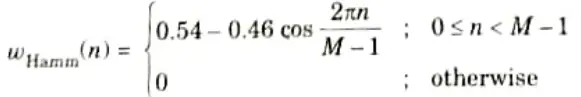
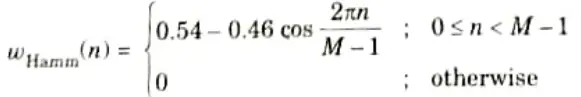
b. Non-causal Hamming window :
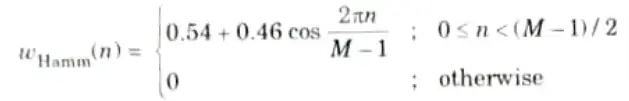
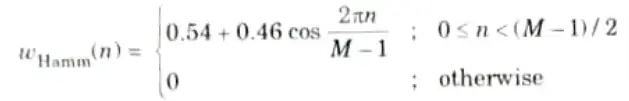
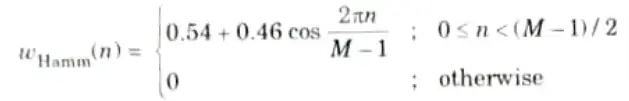
Q9. What are the advantages of frequency sampling method of FIR filter design ?
Ans. i. Simple method of design.
ii. Simple realization in frequency domain.
iii. Better control over eritical frequencies 𝝎p and 𝝎s.
Q10. What is the criteria for selecting a window?
Ans. The specific window is chosen based on the minimal stop band attenuation.
Q11. Suppose the axis of symmetry of impulse response h(n) lies half way between two samples. Identify the kind of applications in which this type of impulse response can be used.
Ans. An impulse response of this type can be utilized to create Hilbert transformers and differentiators.
Q12. Why transition bands are provided ?
Ans. As the ideal filter (zero transition band) is not attainable in a physical sense, transition bands are offered.
Q13. What are the types of limit cycles ?
Ans. There are two types of limit cycles
- i. Lero input limit cycle.
- ii. Overflow limit cycle.
Q14. What are the advantages of Kaiser window ?
Ans. By adjusting the form factor while maintaining a fixed window length, we may create designs that account for pass band and stop band ripples.
Unit-IV: DFT & FFT (Short Question)
Q1. What is discrete time fourier transform and how it is related to discrete fourier transform ?
Ans. A. DTFT:
- 1. The discrete-time fourier transform (DTFT) or, simply the fourier transform of a discrete time sequence x(n) is represented by the complex exponential sequence [e-j𝛚n ] where 𝛚 is the real frequency variable.
- 2 The time-domain sequence can be mapped into a continuous function of a frequency variable using this technique.
B. Relation between DTFT and DFT:
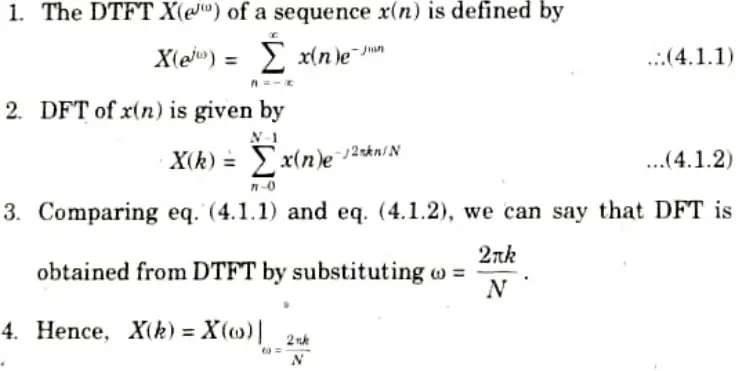
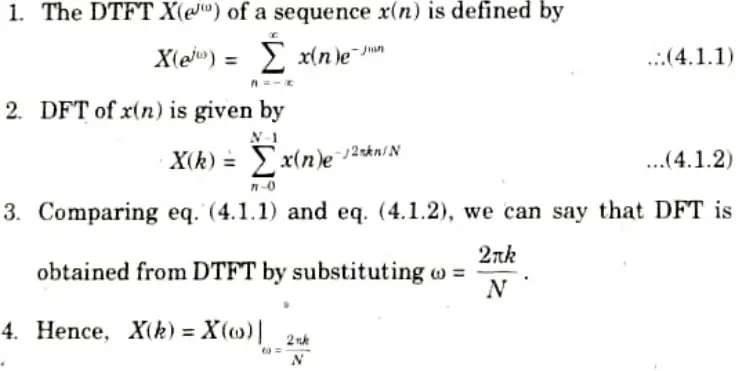
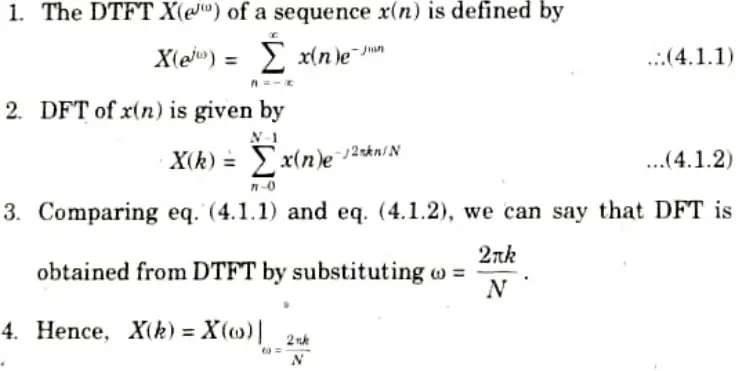
Q2. Define time reversal of sequence in DFT.
Ans.



Hence, when the N-point sequence in time is reversed, it is equivalent to reversing the DFT values.
Q3. Compare DTFT and DFT.
Ans.



Q4. Define linear convolution and its physical significance.
Ans. A. Linear convolution:
Let us consider two finite duration sequences x(n) and h(n), the linear convolution of x(n) and h(n) is given as
y(n) = x(n) * h(n)
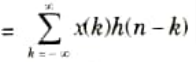
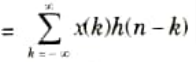
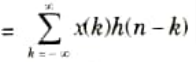
B. Physical significance: Linear convolution can be used to find the response of a filter.
Q5. What is the difference between circular convolution and linear convolution ?
Ans.
| S. No. | Linear convolution | Circular convolution |
| 1. | If the length of one signal is N1 and the length of other signal is N2 then the length of output signal y(n) is N1 + N2 -1. | If the length of one signal is N1 and the length of other signal is N2 then the length of output signal is maximum of both signal (either N1 or N2). |
| 2. | Linear convolution is the term used to describe the time-domain multiplication of two sequences. | Circular convolution is the term used to describe the frequency domain multiplication of two sequences. |
Q6. What is zero padding and what are its uses ?
Ans. A. Zero padding: Let the sequence x(n) has a length L. If we want to find the N- point DFT (N > L) of the sequence x(n), we have to add (N – L) zeros to the sequence x(n). This is known as zero padding.
B. Uses:
- i. We can get “better display” of the frequency spectrum.
- ii. With zero padding. the DFT can be used in linear filtering.
Q7. What is spectral leakage ? Give remedy to this problem.
Ans. 1. The convolution of S(f) and another function, which unavoidably results in the creation of new frequency components, yields the spectrum of a product. The effect of windowing, which is the result of combining s(t) with a different type of window function, is what the term “leakage” normally refers to.
2. To reduce spectral leakage, a smoothing window is added to the data before it is converted into the frequency domain.
Q8. Establish the relation between z-transform and DFT.
Ans. The z-transform for a sequence x(n) is given by



The DFT of x(n) is given by
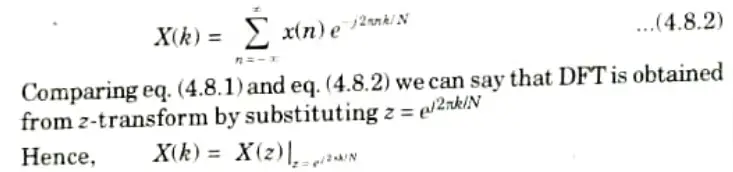
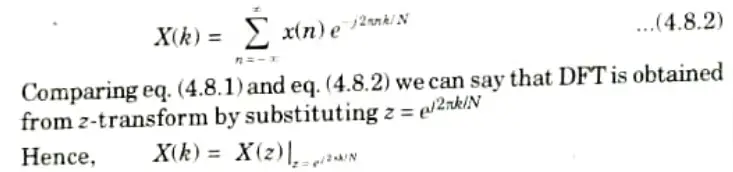
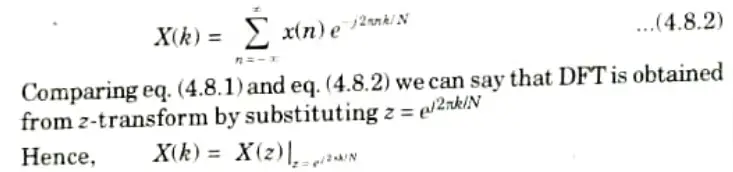
Q9. What is twiddle factor in DFT?
Ans.
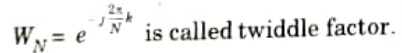
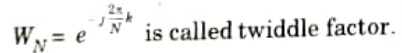
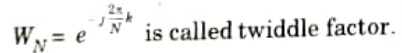
Q10. Draw a transformation matrix of size 4 x 4 and explain the properties of twiddle factor.
Ans. A. Transformation matrix:
For N = 4, Wnk4 is 4 x 4 matrix and is given as
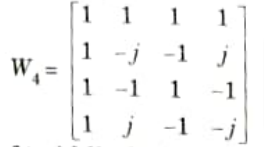


B. Properties of twiddle factor:
i. Symmetry property
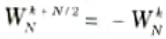
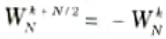
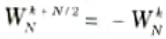
ii. Periodicity property
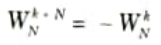
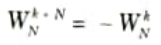
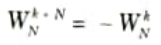
Q11. Write the expression for computation efficiency of an FFT.
Ans.



Q12. Compare DIT and DIF FFT algorithm.
Ans.
| S. No. | DIT FFT | DIF FFT |
| 1. | The time domain sequence is decimated. | The DFT X(k) is decimated. |
| 2. | Input sequence is to be given in bit reversed order. | The DFT at the output is in bit reversed order. |
| 3. | Suitable for calculating inverse DFT. | Suitable for calculating DFT. |
Q13. Explain bit-reversal and in-place computation.
Ans. A. Bit-reversal: In the Fast Fourier Transform (FFT) methods for decimation-in-time (DIT) and decimation-in-frequency (DIF), bit-reversal is useful for moving the data. The order of the bits is reversed during bit reversal.
B. In-place computation: An in-place algorithm is one that transforms input without the use of an additional data structure. Nonetheless, auxiliary variables are given a very little amount of additional storage space. Typically, while an algorithm runs, the output replaces the input.
Q14. Compute X(0) if X(k) is 4-point DFT of the following sequence
x(n) = {1, 0, -1, 0}
Ans.
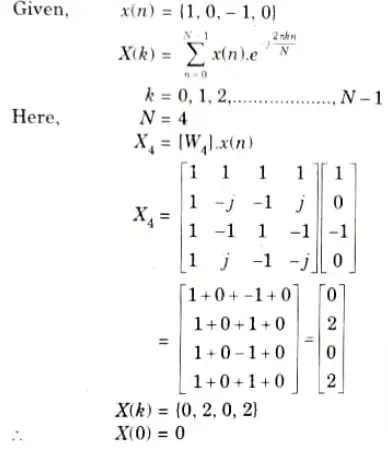
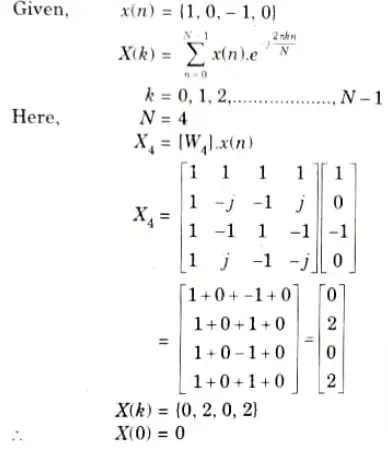
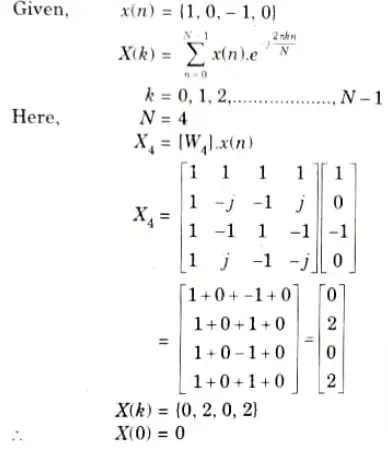
Q15. What is the DFT of 𝛿(n)?
Ans.



Q16. If x(n) = {6, 5, 4, 3} what will be x((2-n))4.
Ans. Given: x(n) = {6, 5, 4, 3)
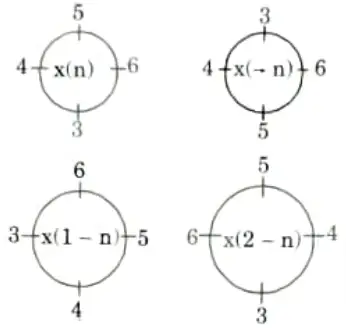


x((2- n))4 = (4, 5, 6, 3)
Q17. If x(n) = (1, 5, 2, 3) what will be x((3-n))4.
Ans. Given: x(n) = {1, 5, 2, 3}
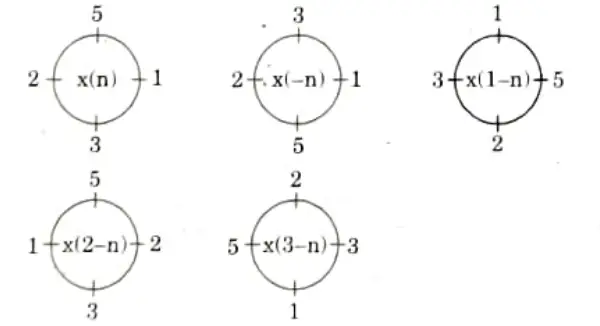


x((3 – n))4 = {3, 2, 5, 1}
Unit-V: Multirate Digital Signal Processing (Short Question)
Q1. What is multirate digital signal processing ?
Ans. Signal averaging (sa) is the process of changing a signal from one rate to another. Multirate digital signal processing systems are used to process digital signals at various sample rates.
Q2. Write uses of multirate digital signal processing.
Ans. i. It is used in design of phase shifter.
ii. A multirate signal processing system can connect digital systems that operate at various sampling rates.
Q3. Define decimation.
Ans. Decimation is the process of lowering the sampling rate by a factor D (downsampling by D).
Q4. Write a short note on interpolation.
Ans. Interpolation is the process of raising the sampling rate by the integer I (upsampling by I).
Q5. What is downsampling and upsampling?
Ans. Downsampling: It is the procedure for decreasing a signal’s sampling rate. Usually, this is done to decrease the data rate or the amount of data.
Upsampling: In order to boost the sampling rate, zero-valued samples are inserted between the original samples.
Q6. Write the advantages of multirate digital signal processing.
Ans. 1. A decrease in the amount of computation and memory needed.
2. Multirate DSP offers a more versatile, efficient, and distortion-free kind of signal processing.
Q7. What is use of Decimation ?
Ans. 1. Reduce the ADC data rate to practical levels to capture data.
2. Keep output sampling rates at a high level for more adaptable frequency planning.
Q8. What is sampling rate conversion ?
Ans. Sampling rate conversion is the process of converting a signal from one rate to another.
Q9. Draw the block diagram of sampling rate conversion.
Ans.
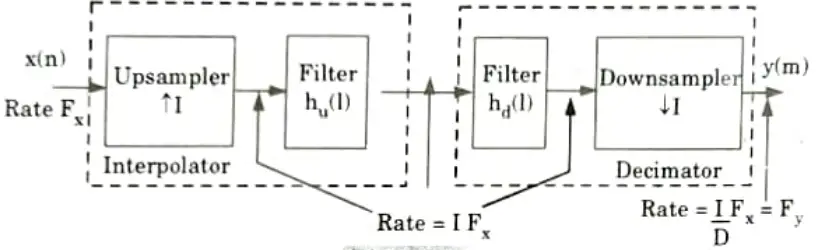


Q10. Write a short note on subband coding of speech signals.
Ans. It’s a technique where the spoken stream is split up into different frequency bands and digitally encoded separately for each band.
Q11. What do you mean by quadrature mirror filter bank?
Ans. Prior to processing, the subband signals are downsampled. Thereafter, the signals are upsampled. The Quadrature Mirror Filter (QMF) bank is the structure utilized for this.
Q12. What is the uses of quadrature mirror filters ?
Ans. 1. Most frequently, a filter bank that divides an input signal into two bands uses a quadrature mirror filter.
2. The resulting high-pass and low-pass signals are often reduced by a factor of 2, giving a critically sampled two channel representation of the original signal.
Q13. If x(n) = {4, 3, 5, 7, 4. 6} and upsampling factor = 3, then what will be the value of upsampler output.
Ans. Given, x(n) = {4, 3,5, 7, 4, 6}
And, M = 3
Output y(n) = x(n/3)
y(n) = {4, 0, 0, 3, 0, 0, 5, 0, 0, 7, 0, 0, 4, 0, 0, 6}



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Digital Signal Processing Btech Quantum PDF, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Question paper – 2021-22 | 2021-22 |
Digital Signal Processing Quantum PDF | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One View) | Student Result |