Here, we’ll talk about some short questions with answers from the Basic Signals and Systems notes. You should find this article useful for your upcoming exams.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Basic Signals and Systems : *Unit-01 *Unit-02 *Unit-03 *Unit-04 *Unit-05 *Short-Q/Ans *Question-Paper with solution 21-22
Unit – 1 (Continuous Time Signals & Systems)
Q1. Define signal.
Ans. A signal is an information-conveying single-valued function of one or more variables.
Q2. What are various types of signals?
Ans. Types of signals:
- 1. Continuous-time and discrete-time signals
- 2. Periodic and non-periodic signals
- 3. Energy and power signals
- 4. Even and odd signals
- 5. Causal and non-causal signals.
Q3. Define CT signals.
Ans. Continuous-time (CT) signals are those that are defined for every instant of time.
Q4. What do you mean by signals? Explain periodic and aperiodic signal with examples.
Ans. A signal is an information-conveying single-valued function of one or more variables.
B. Periodic and aperiodic signals:
1. Periodic signals are those that repeat themselves after a predetermined amount of time.
2. Aperiodic signals are those that do not repeat after a certain amount of time.
3. Example: Periodic signal, x(t) = sin t
Aperiodic signal, x(t) = e-t
Q5. Define unit step, ramp and delta functions for CT.
Ans. 1. Unit step: It is defined as
2. Unit ramp: It is defined as
3. Unit impulse (Delta function): It is defined as
Q6. Check the periodicity of the signals given below:
x(t) = sin (8t- 1) – sin (3t – 1)
Ans. 1. Given; x(t) = sin(8t – 1)- sin(3t- 1)
2. Let x(t) = x1(t)-x2(t)
3. Now x1(t) = sin(8t -1)
Comparing with,
Q7. Draw the signal x(t) = u(t)- u(t-3).
Ans.
Q8. Differentiate between invertible and non-invertible system.
Ans.
| Invertible system | Non-invertible system |
| An invertible system is one that has a particular relationship between its input and output. | A non-invertible system is one that lacks a specific relationship between its input and output. |
Q9. Define time invariant and time varying systems.
Ans. A. Time invariant system: A system is considered time invariant if its input/output properties do not alter over time.
B. Time varying system: If a system’s input/output properties fluctuate with time, it is said to be time varying.
Q10. Define odd and even signal.
Ans. A continuous-time signal x(t) is said to be even if
Q11. Define static and dynamic system.
Ans. A. Static system: If a system responds solely to current input, it is said to be static.
B. Dynamic system: If a system’s response is based on current or historical inputs, it is said to be dynamic.
Q12. A signal x(t) = cos 2𝝅 ft is passed through a device whose input-output is related by y(t) = x2(t). What are the frequency components in the output ?
Ans.
The frequency components at the output are 0 Hz (i.e., DC) and 2f Hz.
Q13. What is the condition for the stability of a system ?
Ans. For a system to be stable, its input and output should be constrained.
Q14. Define linear and non-linear systems.
Ans. A. Linear system: A linear system is one that complies with the superposition and homogeneity principles.
B. Non-linear system: A non-linear system is one that disobeys the superposition and homogeneity principles..
Q15. Check whether the given system is causal and stable y(n) = 3x(n – 2) +3x(n + 2).
Ans. Since y(n) depends upon x(n + 2), this system is noncausal. As long as x(n – 2) and x(n +2) are bounded, the output y(n) will be bounded. Hence this system is stable.
Q16. What is the necessary condition for an LTI system to be stable ?
Ans. For an LTI system to be stable:
Q17. What will be analogous of damping in f-v model ?
Ans. The analogous of damping in f-v model is resistance.
Unit – 2 (Fourier Transform Analysis)
Q1. What is Fourier series ?
Ans. The phrase “Fourier series” refers to the linear combination of orthogonal functions used to describe signals over a given period of time.
Q2. Write Dirichlet’s conditions for the existence of Fourier series.
Ans. 1. Dirichlet’s conditions are the circumstances in which a periodic signal can be represented by a Fourier series.
2. They are as follows: In each period,
i. The function x(t) must be a single valued function.
ii. The function x(t) has only a finite number of maxima and minima.
iii. The function x(t) has a finite number of discontinuitiees.
iv. The function x(t) is absolutely integrable over one period, that is
Q3. Discuss even symmetry and odd symmetry.
Ans. A function x(t) is said to have even symmetry, if x(t) = x(-t).
A function x{t) is said to have odd symmetry, if x(-t) =-x(t).
Q4. State and prove time shifting property of fourier series.
Ans. Time shifting: The time shifting property states that if a signal x(t) is shifted by t0 sec, the spectrum is modified by a linear phase shift of slope -𝝎t0, i.e.,
Proof: By definition,
Q5. Differentiate between Fourier series and Fourier transform.
Ans.
| S. No. | Fourier series | Fourier transform |
| 1. | It is only applicable for periodic signals. | Both periodic and non-periodic signals can use it. |
| 2. | The spectrum is discrete in nature. | The spectrum is continuous in nature. |
Q6. What do you understand by Fourier transform ?
Ans. Using the Fourier transform, signals can be converted from the continuous-time domain to the frequency domain and vice versa.
Q7. Define the Fourier transform pair for continuous time signal.
Ans. Fourier transform:
Inverse Fourier transform:
Q8. Give the applications of Fourier transform.
Ans. 1. Analysis of LTI systems
2. Cryptography 3. Signal analysis
4. Signal processing 5. Astronomy.
Q9. What is interpolation in sampling ?
Ans. Interpolation is the process of reconstructing a continuous-time signal x(t) from its sampled equivalent.
Q10. What are the applications of sampling theorem ?
Ans. Signal analysis, processing, and transmission all require the sampling theorem.
Q11. What are the necessary and sufficient conditions for existence of DTFT?
Ans. The necessary and sufficient conditions for the existence of DTFT is that the sequence x[n] should be absolutely summable. That is
then DTFT exists.
Unit – 3 (Laplace Transform Analysis)
Q1. What do you mean by Laplace transform?
Ans. Laplace transform is a technique which converts a time-domain signal into frequency-domain signal. Let x(t) is defined for –
Q2. Give the advantages and disadvantages of Laplace transform.
Ans. A. Advantages:
1. Signals that converge in the Laplace transform but not in the Fourier transform.
2. A system’s integral differential equations can be reduced to straightforward algebraic equations. Laplace transforms can therefore be used to quickly investigate LTI systems.
B. Disadvantages:
1. Laplace domain’s integral representation is challenging.
2. The system’s frequency response cannot be approximated or drawn. Only the pole-zero layout can be drawn in its place.
Q3. Mention the applications of Laplace transform.
Ans. 1. It is a method that is primarily used in engineering for system modeling where a big differential equation needs to be solved.
2. It is widely used in electrical engineering and can also be used to solve differential equations.
3. It is applied to the analysis of linear time-invariant systems in electrical circuits.
Q4. Define initial value theorem for Laplace transform.
Ans. This theorem enables us to determine the initial value of a function x(t) directly from its Laplace transform X(s)
It states that
Q5. State convolution theorem.
Ans. Convolution theorem states that if there are two functions given by f1(t) and f2(t) which are zero for t < 0 and their Laplace transforms are
Q6. Find the Laplace transform of e-at for t ≥ 0.
Ans.
Q7. Determine the initial value x(0+) of the following Laplace transform.
Ans.
Q8. Find the ROC of x(t) = e2t u(t) + e-3t u(t).
Ans.
Q9. Deduce inverse Laplace transform of 1/s(s + 4).
Ans. 1. Taking Partial fraction of,
2. On solving partial fraction, we get
3. Inverse Laplace transform of,
Q10. Write the s-domain transfer function of a first order system.
Ans.
Unit – 4 (State Variable Analysis)
Q1. What do you mean by state of system ? Also explain state variables.
Ans.
i. State: The state of a dynamic system is the smallest set of variables such that the knowledge of these variables at t = t0 with the knowledge of the input for t ≥ t, completely determines the behaviour of the system for any time t ≥ t0.
ii. State variables: State variables are the factors that contribute to the dynamical system’s determination of its state.
Q2. What is the significance of state variable ?
Ans. Because they supply the data necessary to make both the response and state equations definite, state variables are of essential importance.
Q3. What do you mean by state vector ?
Ans. These n state variables may be regarded as n components of a vector x if n variables are required to fully characterize the behaviour of a particular system. State vector refers to such a vector.
Q4. Give the equation of transfer matrix in state variable analysis.
Ans. Transfer matrix
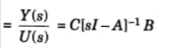
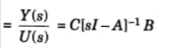
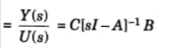
where, A is the system matrix of order (n x n).
B is the input coupling matrix of order (n x 1).
C is the output coupling matrix of order (1 x n).
Q5. List the advantages of state space representation of linear systems.
Ans. 1. It is applicable to time-varying and non-linear systems.
2. Multiple input, multiple output systems can readily use it.
3. The process considers the impact of each initial circumstance.
Q6. Explain homogeneous system.
Ans. If in a state model of a system, A is a constant matrix and input control forces are zero then the equation takes the form, X(t) =A X(f), such an equation is called homogeneous equation and the system is called homogeneous system.
Q7. Discuss non-homogeneous system.
Ans. When input control forces are given to a system and A is a constant matrix in the system’s state model, the system is said to be a non-homogeneous system.
Q8. Explain state transition matrix.
Ans. The matrix ϕ(t) = exp(At) is an n x n matrix and it helps in transition from initial state X(0) to any other state X(t) for t > 0, hence ϕ(t) is called state transition matrix.
Q9. Give the physical significance of state transition matrix.
Ans. It is useful for getting zero input response of the multi-input system.
Q10. Write the properties of state transition matrix.
Ans.
Unit – 5 (Z-transform Analysis)
Q1. What do you mean by Z-transform and inverse Z-transform ?
Ans. A. Z-transform: It converts discrete signals from time-domain to frequency-domain. For a discrete-time signal x[n], Z-transform is given as,
B. Inverse Z-transform: It converts discrete signals from frequency- domain to time-domain.
Q2. List the methods that are used to determine the inverse Z-transform.
Ans. 1. Long Division method.
2. Partial fraction expansion method.
3. Residue method.
4. Convolution method.
Q3. Give the limitation of Z-transform.
Ans. The Z-transform has the drawback that it cannot plot or achieve frequency domain response.
Q4. What is region of convergence ?
Ans. The set of z values in the z-plane for which the magnitude of X(z) is finite is referred to as ROC.
Q5. Explain the properties of ROC of Z-transform.
Ans. 1. The ROC is a ring in the z-plane centred at the origin.
2. The ROC cannot contain any poles.
3. The ROC must be connected region.
Q6. Find the Z-transform of f(nT) = e-anT; a > 0, n ≥ 0.
Ans.
Q7. Derive time reversal property of Z-transform.
Ans. The time reversal property of Z-transform states that
Q8. State the convolution property for continuous and discrete time domain signal in Z-transform.
Ans. According to this fact, the convolution of two discrete-time signals can be described as a straightforward multiplication of the Z-transforms of the signals.
Q9. State the initial and final value theorem for Z-tránsform.
Ans. 1. Initial value theorem:
If limit exists then,
2. Final value theorem:
Q10. Discuss Parseval’s relation.
Ans. The Parseval’s relation of Z-transform states that
Q11. Compare and Z-transform Laplace transform.
Ans.
| S. No. | Z-transform | Laplace transform |
| 1. | LTI discrete-time system analysis is done using it. | It is applied to LTI continuous-time system analysis. |
| 2. | The ROC of X is the range of z values for which X(z) converges (z). | The ROC of X is the set of values ofs for which X(s) converges (s). |



Important Question with solutions | AKTU Quantums | Syllabus | Short Questions
Basic Signal And System Quantum, Syllabus, Important Questions
| Label | Link |
|---|---|
| Subject Syllabus | Syllabus |
| Short Questions | Short-question |
| Important Unit-1 | Unit-1 |
| Important Unit-2 | Unit-2 |
| Important Unit-3 | Unit-3 |
| Important Unit-4 | Unit-4 |
| Important Unit-5 | Unit-5 |
| Question paper – 2021-22 | 2021-22 |
Basic Signal And System Quantum PDF: | AKTU Quantum PDF:
| Quantum Series | Links |
| Quantum -2022-23 | 2022-23 |
AKTU Important Links | Btech Syllabus
| Link Name | Links |
|---|---|
| Btech AKTU Circulars | Links |
| Btech AKTU Syllabus | Links |
| Btech AKTU Student Dashboard | Student Dashboard |
| AKTU RESULT (One VIew) | Student Result |

1 thought on “Short Questions Basic Signals and Systems notes | AKTU”